Space-time patterns are shown. From an initial one-dimensional configuration of cell states the Cellular Automaton proceeds its way along discrete time-steps according to a RULE. In these particular cases the neighborhood of each cell (i.e. its ' wiring') consists of five cells (itself included) : k = 5. The size of the system is 900 (n = 900), which means that the system consists of a row of 900 cells which are updated after every discrete time-step.
We must read each space-time pattern from top to bottom (In the displays of these space-time patterns, all previous (one-dimensional) patterns remain displayed, so that we can easily see the evolution of the system).
Directly following each Space-time pattern of Ordered, Complex and Chaotic CA's, the respective Basin of Attraction Fields (of Ordered, Complex and Chaotic CA's respectively) are shown, but in this case for systems only consisting of sixteen cells (n = 16). This is because for larger systems it becomes practically impossibe to compute their Basins of Attraction Fields. See the pictures below.

Space-time pattern of an Ordered CA. k = 5 rule 01dc3610, n = 900
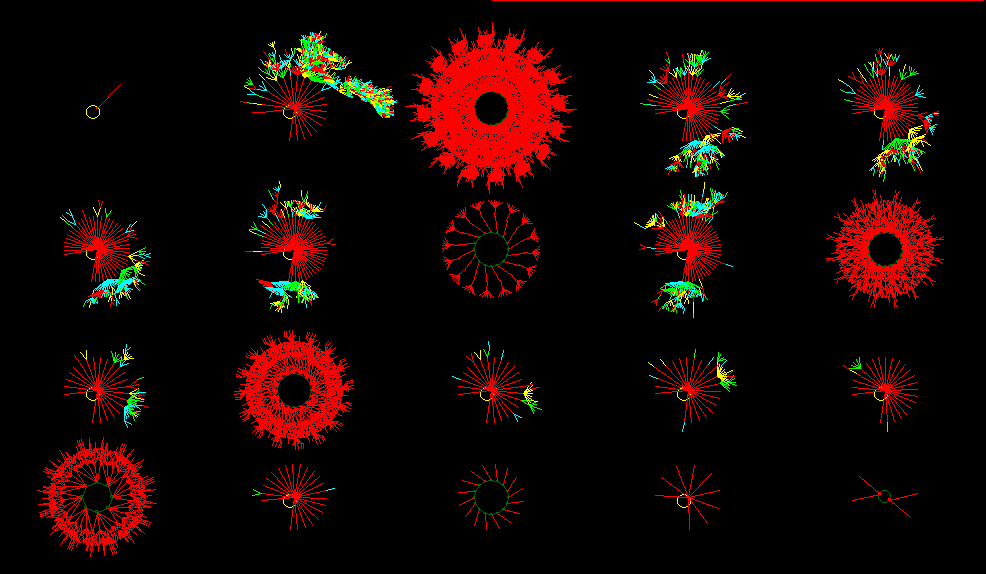
Basin of Attraction Field of an Ordered CA. n = 16

Space-time pattern of a Complex CA. k = 5 rule 6c1e53a8, n = 900

Basin of Attraction Field of a Complex CA. n = 16
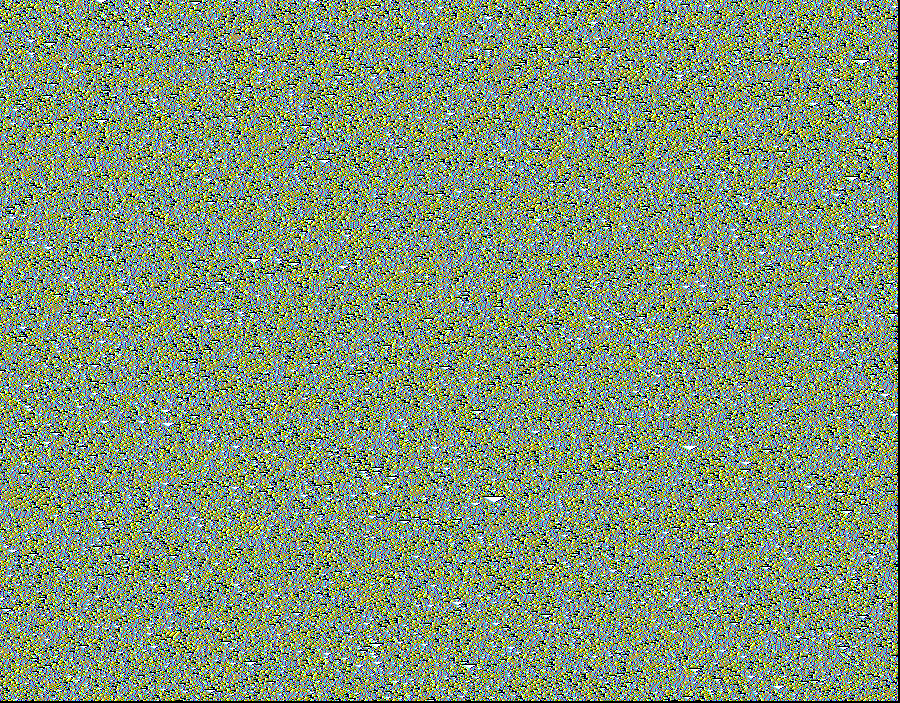
Space-time pattern of a Chaotic CA. k = 5 rule 994a6a65, n = 900
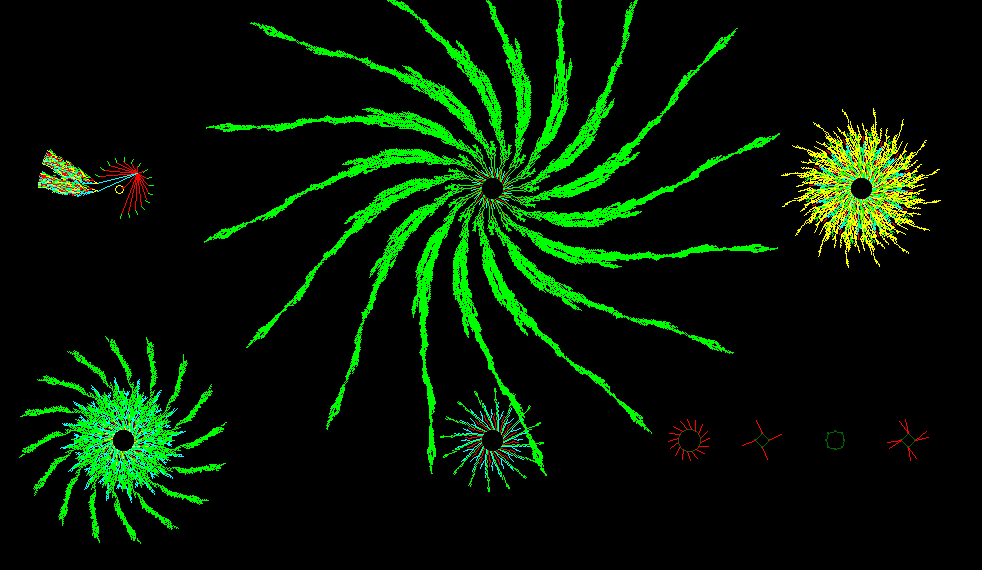
Basin of Attraction Field of a Chaotic CA. n = 16
back to main text
.