back to homepage
The symmetry of regular 2-D arrays of repeated motifs (continued)
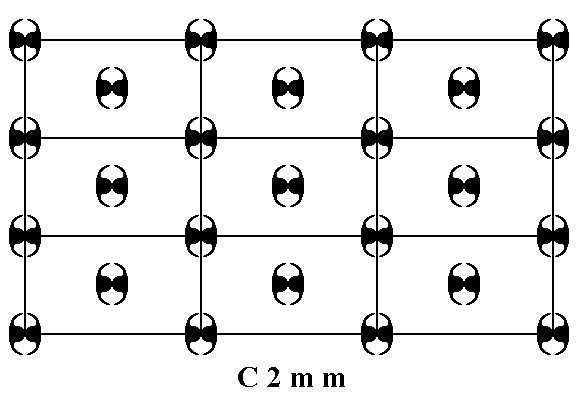
Placing motifs with 2mm symmetry in a centered rectangular net (= centered rectangular 2-D lattice) yields the Plane Group C2mm. See Figure 1.

Figure 1. Placing motifs with point symmetry 2mm in a centered rectangular net, yields a periodic array of motifs representing Plane Group C2mm.
As in all cases the pattern must be imagined to be extended indefinitely across the two-dimensional plane.
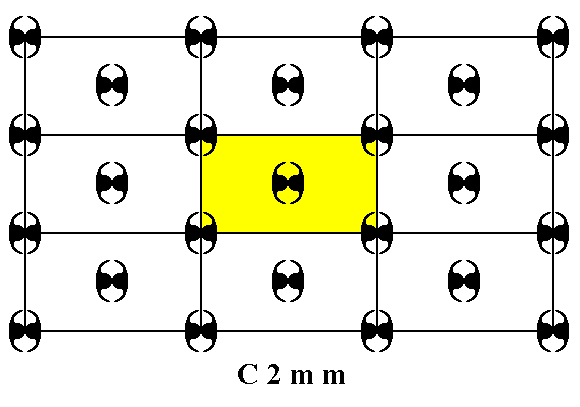
Figure 1a. A unit mesh choice is given (yellow). This unit mesh has point symmetry 2mm, and is centered.
If we eliminate all translations from the pattern representing Plane Group C2mm, then we end up with a figure that has point symmetry 2mm. So the Point Group associated with that Plane Group is indeed 2mm. See Figure 1b.

Figure 1b. The translation-free residue of the pattern representing Plane Group C2mm. The resulting figure represents Point Group 2mm.
The unit mesh, as given in Figure 1a, contains two motifs s.str. (1 + 1/4 + 1/4 + 1/4 + 1/4). The whole unit mesh with its content can be considered as the motif s.l. that tiles the 2-D plane completely.
Patterns representing the Plane Group C2mm have 2-fold rotation axes, mirror lines and glide lines. See Figures 1c---1f.
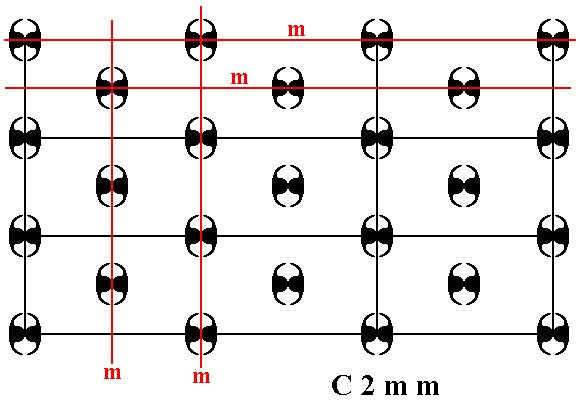
Figure 1c. A pattern representing Plane Group C2mm has mirror lines in the x and y directions. Some of them are indicated (m).
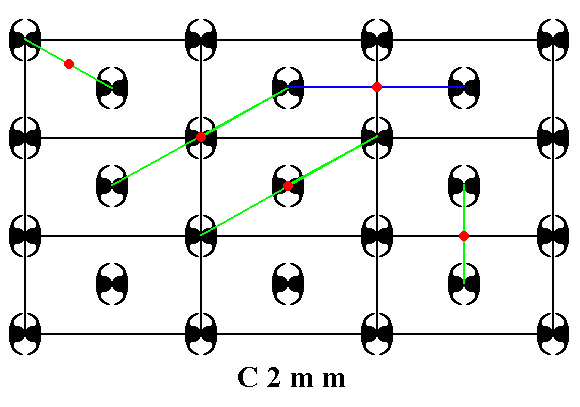
Figure 1d. A pattern representing Plane Group C2mm has 2-fold rotation axes perpendicular to the plane of the drawing. Some of them are indicated (red dots).
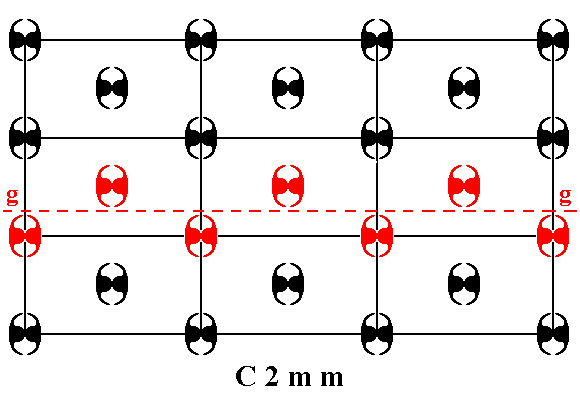
Figure 1e. A pattern representing Plane Group C2mm has glide lines.
One of them is indicated (g).
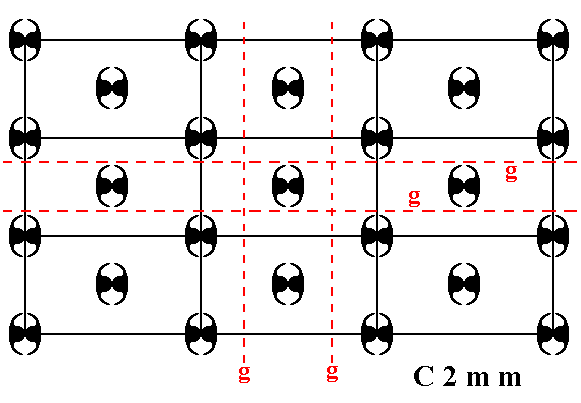
Figure 1f. A pattern representing Plane Group C2mm has glide lines. Some of them are indicated (g).
The total symmetry content of any pattern representing Plane Group C2mm is given in the next Figure.
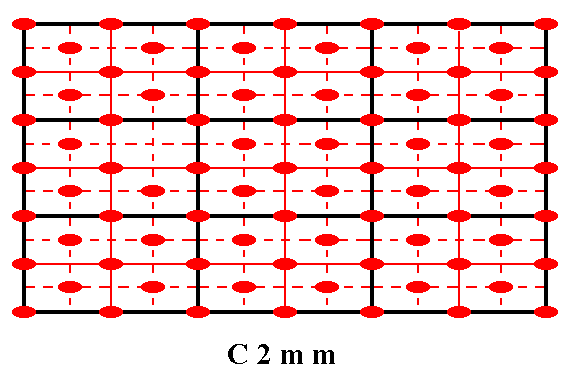
Figure 1g. Total symmetry content of Plane Group C2mm.
2-fold rotation axes perpendicular to the plane of the drawing are indicated by small solid red ellipses.
Mirror lines are indicated by solid lines (black, and red).
Glide lines are indicated by red dashed lines.
So now we have determined the fourth (and last) Plane Group belonging to the Point Group (Crystal Class) 2mm of the 2-D Rectangular Crystal System.
Next we will consider the Plane Groups belonging to the Point Group m of the 2-D Rectangular Crystal System. There are three such Plane Groups possible :
Let's start with the Plane Group Pm.
If we insert motifs with point symmetry m into a primitive rectangular lattice such that every node of that lattice is associated with such a motif, then we get an array of motifs representing the Plane Group Pm. See Figure 2.
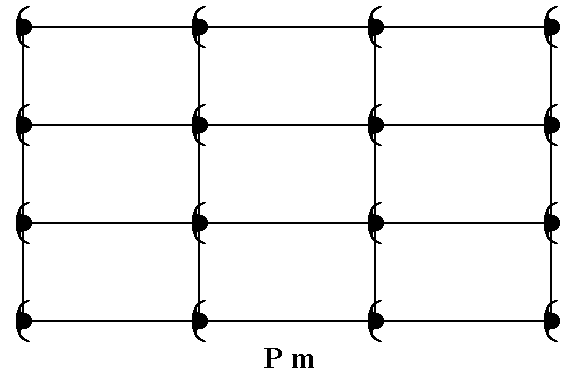
Figure 2. When we place motifs, possessing a point symmetry m , at the nodes of a primitive rectangular net, we get a pattern that represents Plane Group Pm.
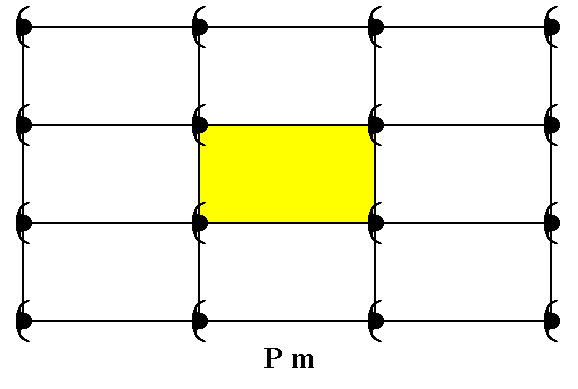
Figure 2a. For the repetitive pattern of Figure 2 a unit mesh is chosen (yellow).
This unit mesh has a point symmetry m , and is primitive.
When all translations are eliminated, all the motifs coincide, and the resulting figure has a point symmetry m, so the Point Group (Crystal Class) associated with this Plane Group is m.
The only symmetry elements, besides simple translation, of this Plane Group are mirror lines parallel to the y direction.
The total symmetry content of the Plane Group Pm is depicted in the next Figure.
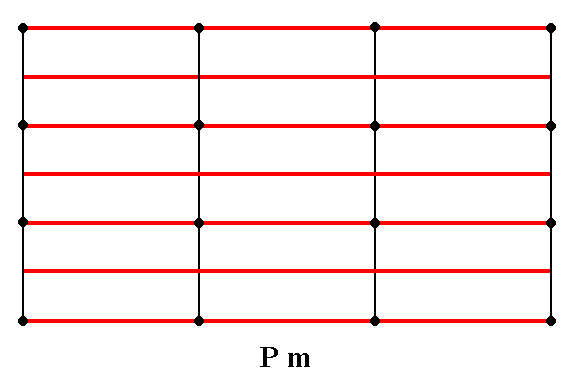
Figure 2b. The total symmetry content of the Plane Group Pm.
The only symmetry elements this Group has are mirror lines parallel to the y direction. They are indicated by red lines.
For clarity the nodes of the lattice are indicated (black dots).
So we have found the first Plane Group (Pm) belonging to the planar Point Group m.
If we place asymmetric motifs (in fact motif units that are symmetric with respect to each other) in a primitive rectangular 2-D lattice (net) such that we let them alternate along the y edges of the unit mesh (and all repetitions of it), then we obtain a pattern that represents the Plane Group Pg. See Figure 3.
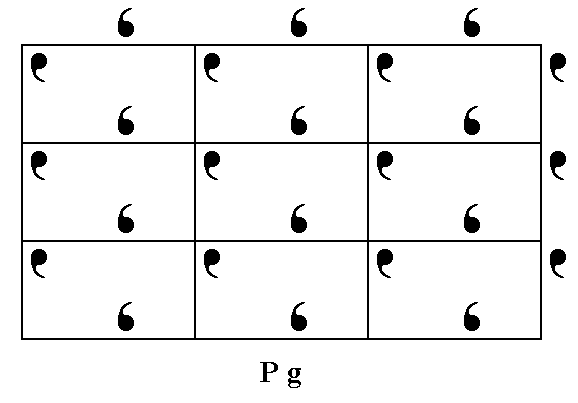
Figure 3. Asymmetric motifs (in fact motif units) placed in a primitive rectangular net, such that they alternate along the y edges of the meshes, produce a pattern that represents the Plane Group Pg.
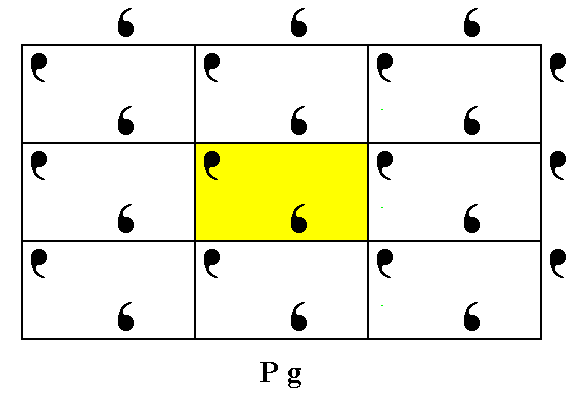
Figure 3a. A unit mesh is chosen (yellow). This unit mesh is primitive and has a point symmetry 1, i.e. it is asymmetric.
When we remove all translations, the individuals of the same type of motif unit will be superimposed upon each other, resulting in only one individual per type. In the present case this means that only two individuals remain, one of each type (= the two types of comma in our Figures), and these two individuals become aligned to each other because of the disappearance of translational distances, and in this way together form a figure that has point symmetry m. Thus the Point Group to which our Plane Group belongs is m. See Figure 3b.
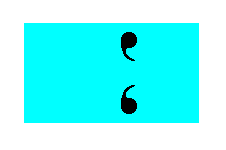
Figure 3b. The translation-free residue of the pattern representing Plane Group Pg has m symmetry (i.e. the only symmetry element it has is one mirror line), and represents the Point Group to which the Plane Group Pg belongs.
The next Figure shows what the very motif (s.str.) actually is, and that it is constituted out of two motif units. This motif, together with its surroundings (such that together they make up the motif s.l.), tiles the 2-D plane completely (shown in Figure 3d).
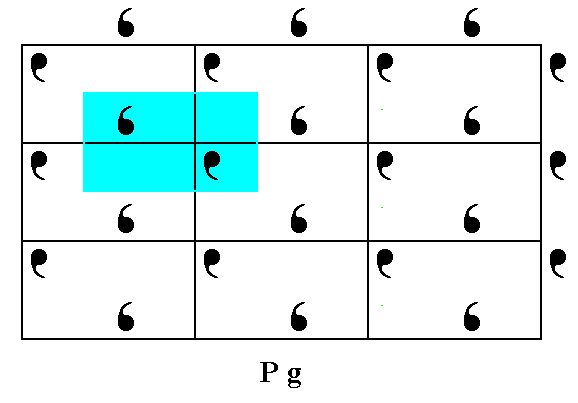
Figure 3c. The real motif, constituting the pattern of Figure 3.
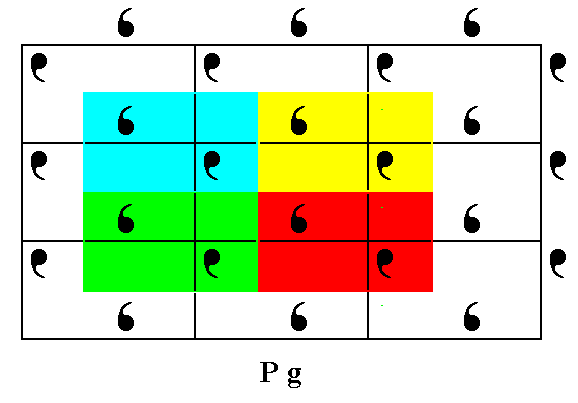
Figure 3d. The real motif s.l. tiles the entire 2-D plane in a periodic fashion.
The only symmetry elements the Plane Group Pg has, are simple translations (in the x and y directions) and glide lines parallel to the y direction. See Figure 3e.
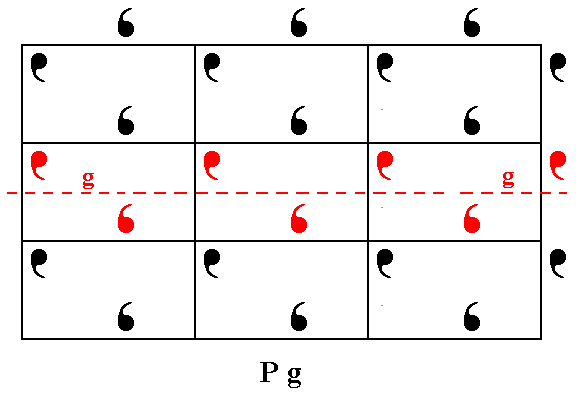
Figure 3e. Patterns representing Plane Group Pg have glide lines parallel to the y direction. One of them is shown.
The total symmetry content of the Plane Group Pg is shown in the next Figure.
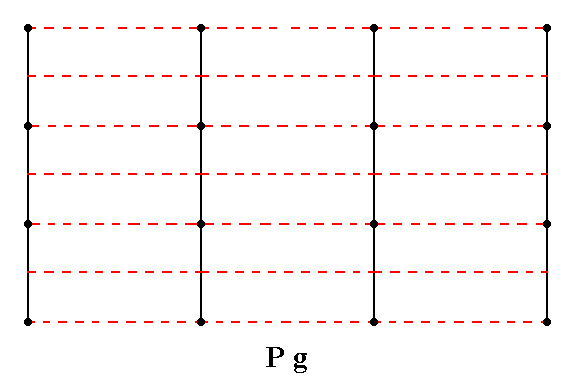
Figure 3f. Total symmetry content of the Plane Group Pg .
Glide lines are indicated by red dashed lines. There are no mirror lines. For clarity the nodes of the net are indicated (black dots).
So we have found the second Plane Group (Pg) belonging to the planar Point Group m.
If we, finally, place motifs that are, like the ones we had in the Plane Group Pm, symmetric, i.e. have a point symmetry m, into a centered rectangular 2-D lattice (net), then we get the Plane Group Cm. See Figure 4.
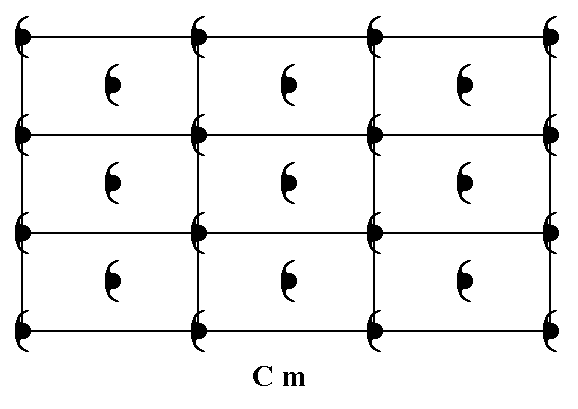
Figure 4. Placing symmetric motifs into a centered rectangular net, such that each lattice node is associated with such a motif, yields a pattern representing Plane Group Cm.
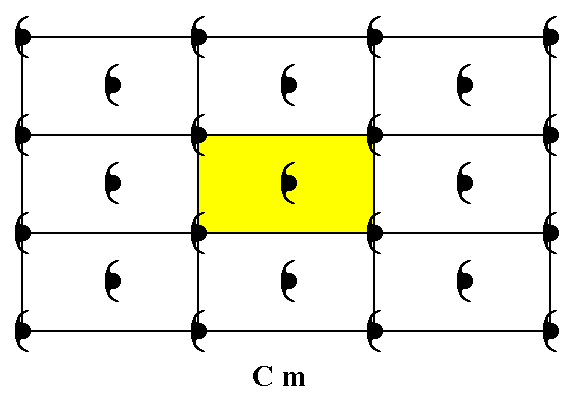
Figure 4a. A unit mesh is chosen (yellow). This unit mesh has point symmetry m and is centered.
If we remove all translations, then all the motifs will be superimposed upon each other, resulting in just one individual motif having the shape of the originally inserted motif individuals. This shape is consistent with a point symmetry m. So the translation-free residue of the Plane Group Cm, i.e. its Point Group, is m.
The symmetry of a pattern representing Plane Group Cm consists of mirror lines and glide lines, all parallel to the y direction. The next Figure illustrates one of the glide lines.
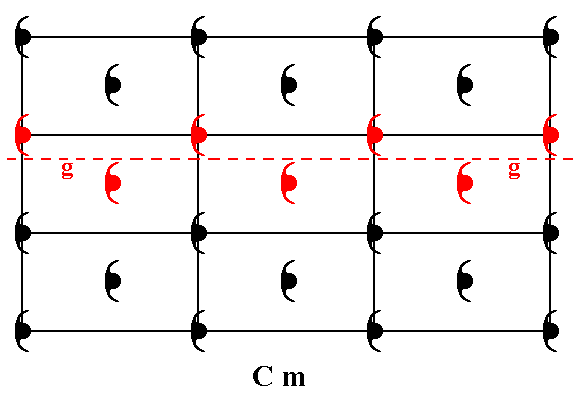
Figure 4b. Patterns representing Plane Group Cm have glide lines. One of them is shown (dashed red line).
The total symmetry content of the Plane Group Cm is shown in the next Figure.
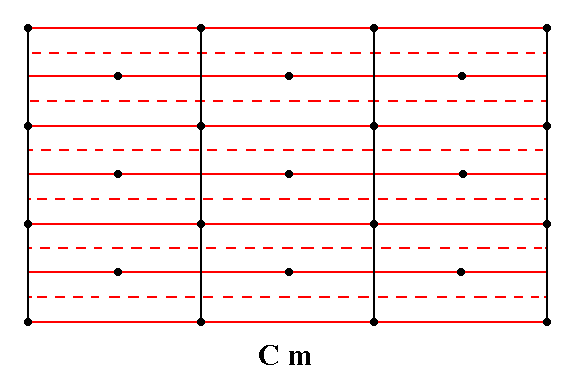
Figure 4c. Total symmetry content of the Plane Group Cm.
Glide lines are indicated by red dashed lines.
Mirror lines are indicated by red solid lines.
All the glide lines and mirror lines are parallel to the y direction.
For clarity the nodes of the net are indicated (black dots).
Now we have considered all three Plane Groups belonging to Point Group m.
In the next Part we will consider the insertion of motifs into a Hexagonal Net. This net (2-D lattice) represents the 2-D Hexagonal Crystal System, which has four Classes (Point Groups) and five Plane Groups.
To continue, click HERE for Part Five.
back to homepage