


back to homepage
At very low temperatures we could have crystals composed of atoms of an inert gas, like Helium. In such cases the atoms are packed together forming a regular array, but no genuine chemical bonds are involved. Attraction forces that could be involved are Van der Waals forces. But they are very weak.
True Molecules also are compounds of atoms, here by means of almost exclusively covalent bonds (In proteins disulfide bridges are also important), but here (i.e. in molecules) no exact repetition takes place of a unit in three spatial directions. In large molecules repetitions at a local scale do, it is true, often occur, but here it is always a matter of being repeated a specific number of times, while this number is not fixed in crystals. Moreover a repetition of units in molecules does not necessarily have to be a repetition in all three spatial directions, and also not necessarily one with the same orientation of the repeated units.
An Organism is a complex Totality. It is an open dynamical system which cannot be in a state of lowest energy (while crystals and molecules can). It always finds itself far from thermodynamic equilibrium. However this does not prevent organisms to be composed of molecules, and their functioning wholly to be contained within these molecules and their interactions. In organisms the molecules are organized in different ways. They together can form all kinds of static or dynamic aggregations, in virtue of physical forces. In general they form functional structures above the molecular level, in which also single molecules play a role. All this leads to organic cells and tissues, level after level.
And because, accordingly, Crystals and Organisms consist of atoms, bonded together in lattices or molecules, the understanding of the chemical bonding of atoms into a next more complex level, i.e. into Crystals or into Molecules, is a first step towards an understanding of the higher Totalities, and these are the Organisms.
REMARK [inserted here in the year 2010] : We said that an organism is a complex totality, consisting of [many different, interacting] molecules. It is a state [one or the other] of a particular dynamical system, in which [state] the elements of that dynamical system have been re-arranged and [often] transformed, as a result of interaction of these elements with one another.
It might, however, be questioned whether mere rearranged and changed elements together can form a single totality, a single Substance, at all. And, indeed they can, provided that they, upon their integration into the totality, become virtual, meaning that they, instead of elements of the totality, become properties of that totality. So the elements merge into the one single totality which itself is but one single being (ens). In this sense the organism is a heterogeneous continuum (where "continuum" here means : metaphysically being continuous, i.e. being one single ens). But, how, in the organism, will its "being a totality, being a metaphysical continuum, being an intrinsic unity", be, if at all, concretely expressed? Where, in the organism, do we actually see this unity? What, in the organismic body, is evidence of this unity, of this totality-nature? In totalities beyond the level of chemical atoms, i.e. in molecules, their intrinsic unity, rendering them to be true totalities instead of mere aggregates, is evident by the atoms in such a molecule being chemically bonded with each other. And indeed, it seems that true intrinsic unity in a given being can only be accomplished by its elements to be chemically bonded. And thus we might expect that the intrinsic unity of an organism is also accomplished by the chemical bonding of its atoms. And this suggests that an organism is not a pattern of (interacting) molecules (and ions or atoms), but a single molecule. However, there evidenty do exist in the organismic body also free molecules (and ions). Indeed, much of the organismic body is water, H2O, i.e. free molecules. But of course also many other free molecules do exist in the organismic body such as enzymes, hormones, RNA molecules, etc. They all occur as solutions in body fluids. Now, from the demand that the organism as a whole is a single totality, we may stipulate that just as the molecules and atoms that actually constitute the organismic body are not actual constitual corpuscular elements of the organismic body anymore but simply properties of that body, we may view the free molecules and atoms, as they are present in the organismic body, not as corpuscular entities in that body, but also as properties of that same body. So they, i.e. the "free molecules and atoms", are, in contrast to the aforementioned "constitutive" molecules, only metaphysically connected with each other and with the rest of that body. They are metaphysically connected with each other (and only metaphysically so connected) because the organismic body is supposed to be one single intrinsic unity. And this "only metaphysically be connected" (of the organismic body's free molecules and atoms) is, in virtue of its very nature, not directly and concretely expressed and visible in the organismic body. And precisely because of this "not being concretely expressed" we may, instead of confirm, deny any direct connectedness between these free molecules and atoms among themselves and with the rest of the organismic body. What is left, then, of "direct connectedness of constituents" of the organismic body? Well, all the solid or semi-solid macroscopic parts of it : These parts must then be chemically bonded to one another, guaranteeing that division (region) of the organismic body to be a true totality. And this division, this region, of the organismic body then must be one single molecule, a living molecule. And this molecule then must be embedded in an aquous serum-like supporting medium in which indeed reside the mentioned actual free molecules and atoms. This is the so-called Unimol view of the organism, first investigated by Oskar Müller in 1959. Every organism is a single highly complex folded and twisted molecule completely soaked-through with an aquous serum-like supporting medium, mediating that molecule's interaction with its environment. As parts of the organismic body belonging to that single living molecule we may suggest : nervous system, walls of the vascular system, muscle tissue, bones, skin, hairs, nails, horns, cell-walls, etc., while as parts of the organismic body that belong to the supporting medium we may suggest : the content of the blood, the content of the digesting system, all (other) body fluids, fat reserves, etc. These, in themselves dead entities all support the one living molecule. Every macroscopic part of the organismic body, however small, contains part of the living molecule as well as a certain amount of the supporting medium. So the supporting medium is everywhere in the organismic body, and also the one living molecule is everywhere present in that body. This giant protein-like molecule is an entangled interlacement of chains and side-chains of atoms, mainly of the chemical elements carbon (C), hydrogen (H), oxygen (O), and nitrogen (N), everywhere in contact with the organismic body's supporting medium. And thus, in fact, the true organismic totality, in the sense of a single being, is not the organismic body as a whole, but the single giant living molecule in it. And indeed, that molecule's constituents are chemically bonded to one another. And indeed, only the chemical bond is strong enough to render the living molecule's intrinsic pattern and shape to be stable and to be able to reliably fulfill its organic function. And this function in fact boils down to an active strategy to actually exist, even in an unfriendly environment.
All this, i.e the Unimol view of organisms, is extensively discussed from part XVg onwards in Sixth Part of Website (if the reader wants to directly access the mentioned part XVg (of Sixth Part of Website), he or she should click HERE.
( end of REMARK )
The formation of small Totalities, like (small) molecules, then implies the presence of a set of free atoms (i.e. individually existing atoms). Under certain (imaginable) conditions they connect to each other, forming a stable pattern, a molecule. Such a very small Totality has the oddity that relatively many determinations (See for the latter the Essay on Determinations), like for instance size, are per se. This in contradistinction to higher (and thus also bigger) Totalities.
Now, because the precise process that leads up to the formation of small molecules, is nowadays well known, it is for this case well possible to expound what the Dynamical Law (as Dynamical Law) really is, and what the phenomenon of unity of a Totality is all about.
Seen after the fact, the formation of a molecule consists in a transformation of a collection of free atoms - which find themselves in a random spatial configuration -- Of course situated closely enough to each other, to be able to interact. -- (they move about in all directions) - into a fixed stable non-random pattern of those same atoms : They have connected themselves to each other, resulting in a molecule (and this is the new Totality). The connection in this case is chemical, i.e. by means of chemical bonds. Several of such molecules can in turn react with each other, resulting in other molecules, either of the same size, or possibly of a larger size. Both are new Totalities again. The larger molecules are higher-order Totalities.
So it is possible that, in a laboratory say, ten Aminoacids couple together, resulting in a new large molecule, a so-called polypeptide. These polypeptides can chemically connect themselves in turn with other polypeptides to form yet larger complexes, the protein molecules.
In a next to be discussed very simple and imaginary scheme I will try to assess the status and location of the Dynamical Laws involved, Dynamical Laws that play a role in such a (way of) formation of such Totalities. After this is done, the formation of real small Totalities will be expounded.
But let us, before drawing the scheme mentioned, first consider generally the status and location of the Dynamical Law(s) :
The Dynamical Law is distributively and collectively contained in the (collection of) system elements, and so (also) in the elements of the generated Totality. The Dynamical Law does not reside in one ('favorite') of those elements, and also not (wholly completely) in whatever individual element, i.e. the Dynamical Law does not reside (completely) in any (one) element of the reaction system, nor does it (completely) reside in each element of the given system. What then means the 'in' in "is ...contained in the (collection of) system elements"? In what way the Dynamical Law is contained in the system elements? It is contained in (a part of) the properties of those elements in a non-concrete and non-individual way (because it is dispersed over several (i.e. more than one) system elements). And only when certain external conditions are satisfied it is triggered into action resulting in the generation of the Totality. At the level of the system elements of the dynamical system (which will generate the Totality) the Dynamical Law is anchored in aspects of the properties of those elements, and is localized there (i.e. at that level, and with respect to each individual system element) in the phenotypic domain [NOTE 1], i.e. it is localized there as (i.e. in its form of) dispersed aspects of the properties of those elements. But (indeed) as Dynamical Law for (and of) the Totality to be generated, it is localized in the genotypical domain, namely in the genotypical domain of that Totality.
Such Totalities can in turn themselves become system elements of a dynamical system, which generates a new higher-order Totality, and of which the Dynamical Law resides in the phenotypical domain of the former Totalities, but in the genotypical domain of the new higher-order Totality ( However, wherever it is situated, the Dynamical Law is never a concrete entity because of its dispersed way of being.). This is the 'sawtooth model' of the relation between properties and Essence (Dynamical Law). But of course, we can, in the case of the formation of such a higher-order Totality, also trace the Dynamical Law of that higher-order Totality right back to the ultimate constituents of it. In the case of molecules (also higher-order molecules) these are the atoms that ultimately make up that higher-order molecule. We then have to do with only one Dynamical Law, governing the generation of the high-order Totality directly from those atoms. The other, intermediate Laws, are then penultimate Laws.
Now it is time to expound the promised simple (fictitious) scheme concerning the formation of a simple Totality, a formation by an ordering (rearrangement) of system elements which themselves remain in essence the same in the course of the process. So we will investigate here the simple (and hypothetical) case in which a Totality (one, or more, different, Totalities) is generated, just in virtue of pattern formation (regular configuration) of the system elements : (in other words) the elements of the dynamical system are going to organize (order) themselves, resulting in a regular (and that is lawful) pattern, ordered according to a simple principle, a pattern of those same elements. This is, in essence, the case in the formation of molecules. In the process the atoms (the elements of the system) remain what they were, only their periphery undergoes some changes.
Suppose we have a (dynamical) system, D1, consisting of elements A, B, C, D, E, F, G, H, I, J, and K, that are sufficiently close to each other spatially to be able to interact with each other.
Remark : "elements A, B, C, D, E, F, G, H, I, J, and K" should be interpreted here as element species, i.e. individuals representing these different species. Accordingly, in the symbolized dynamical system to be discussed, namely D1, there can be several (i.e. more than one) individuals of A, and also of B, etc.
In certain external conditions (having to do with energy) they are going to move about until a stable regular pattern of them is formed, a non-random configuration of them - I have in mind the formation of a molecule out of atoms - a pattern that from then onwards remains the same. This pattern is here interpreted as a Totality, i.e. not as an aggregate. Let us call it Totality T1. The Dynamical Law for such a pattern to be generated is, as has been said, contained in certain aspects of the set of properties of the system elements. Let us call the just triggered Dynamical Law ST1.
In the case of other external conditions, i.e. different from the former case, the set of properties triggers other interactions, which means the triggering into action of a different (with respect to content) Dynamical Law, say the Dynamical Law ST2, resulting in a different (also - ex hypothesi - non-random) pattern, and thus in a different (with respect to content) Totality, say Totality T2.
So external conditions effect the triggering into action of either that one Dynamical Law (ST1) leading to the generation of Totality T1, or the other Dynamical Law (ST2) leading to the generation of Totality T2 :
Dynamical system D1 :
B J
K
G
I
E
A J
C
F
D
generates through Dynamical Law ST1 the Totality T1 :
A
B C D
E F G
H I J
K
but generates through Dynamical Law ST2 the Totality T2 :
B
C D E
F G H
I J K
A
And of course many other Totalities can in this way be formed from these elements, depending on external conditions.
T1
T2 T3
T4 T5
T6
or :
T2 T4 T6
T8
T10 T12 T14
etc.Let us indicate these new Totalities as :
TTA, TTB, TTC, TTD, TTE, etc.
And the respective Dynamical Laws as :
STTA, STTB, STTC, STTD, STTE, etc.
Also these new Totalities can in turn become the elements of a (dynamical) system, say D3, and then generate the Totalities
TTTA, TTTB, TTTC, TTTD, TTTE, etc.
through the respective Dynamical Laws
STTTA, STTTB, STTTC, STTTD, STTTE, etc.
This process, with the alternation of Dynamical Law, Totality, Dynamical Law, Totality, etc., can in principle continue of course.
When we summarize all this, we get :
Dynamical System D1
Dynamical Laws ST1, ST2, ----------
Totalities T1, T2, ---------
Dynamical System D2
Dynamical Laws STTA, STTB, -----
Totalities TTA, TTB, ----
Dynamical System D3
Dynamical Laws STTTA, STTTB, -----
Totalities TTTA, TTTB, -----
etc.
If we trace one of these Totalities, say, TTTA, back, then we could get for example the following series :
Totality TTTA is generated through
Dynamical Law STTTA from, say,
the Totalities TTA, TTB, TTC, TTD and TTE.
Totality TTA is generated from, say, the
Totalities T1, T5, T6, T7 and T8 .
Totality TTB is generated from, say, the same Totalities T1 and T5 t/m T8, but these same Totalities were rearranged into a different pattern, resulting in a different Totality, in this case TTB .
Totality TTC is generated from the
Totalities T5, T8, T9, T10 and T15,
Totality TTD is generated from the
Totalities T1, T2 and T3, and
Totality TTE is generated from the
Totalities T2, T4 and T11.
All this through the Dynamical Laws STTA, STTB, STTC, STTD and STTE.
The Totalities T1, T2, T3, etc. are generated from the Totalities A, B, C, D, E, F, G, H, I, J and K through the Dynamical Laws ST1, ST2, etc.
So we get the following scheme :
TTTA
*
*
Dynamical Law STTTA
*
*
TTA, TTB, TTC, TTD, TTE
*
*
Dynamical Laws STTA, STTB, STTC, STTD, STTE
*
*
T1, T2, T3, T4, T5, T6, T7, T8, T9, T10, T11, T15
*
*
Dynamical Laws ST1, ST2, ST3, ST4, ST5, ST6, ST7, ST8, ST9, ST10, ST11, ST15
*
*
A, B, C, D, E, F, G, H, I, J, K
So the generation of the Totality TTTA started with the elements A, B, C, D, E, F, G, H, I, J and K, and through the Dynamical Laws
The (immediate) Dynamical Law for the Totality TTTA is STTTA. But this Dynamical Law presupposes, through the Totalities TTA, TTB, TTC, TTD and TTE, the Dynamical Laws STTA ,
STTB, STTC, STTD and STTE.
These Dynamical Laws in turn presuppose the Dynamical Laws ST1, ST2, ST3, ST4, ST5, ST6, ST7, ST8, ST9, ST10, ST11 and ST15 .
So the Dynamical Law STTTA must accordingly be equivalent to the total of Dynamical Laws involved.
In this way the Dynamical Law STTTA is in fact the Dynamical Law which could directly generate the Totality TTTA from the Totalities A, B, C, D, E, F, G, H, I, J and K, ( I.e. from (several) individuals of the Totality species A, ..., K. (See the Remark above).) if certain external conditions are satisfied. But in order to be so it must be analysed in terms of the Dynamical Laws ST1, ST2, ST3, ST4, ST5, ST6, ST7, ST8, ST9, ST10, ST11 and ST
We have described the formation of definite patterns, having in mind atomic patterns. The reason why we devote so much attention in this dissertation to definite and more or less stable patterns which can in principle be repeated across individual cases, is that such a pattern is a direct manifestation of what the thing under consideration really is. That pattern is generated by the Essence of the thing.
In fact all the workings and activities of the World, from the origin and behavior of low pressure weather systems to the behavior of living beings, are rooted in certain definite patterns.
So Being is always associated with pattern.
Now the time has come to say something more about the formation (the constitution) of Totalities in the Real World according to the above scheme or a part thereof. And to begin with, we will follow the formation (seen after the fact) of molecules from atoms, i.e. the formation of a stable ordering of atoms into molecules, in which the atoms essentially remain what they were [NOTE 2], or, said differently, the formation of molecules of a chemical compound out of the initially free atoms which are going to compose that molecule [NOTE 3].
And here we have indeed what holds the World together : The chemical bond.
When we discuss the formation of molecules -- molecules as small Totalities -- and speak about chemical bonds, we presuppose that molecules have a structure, especially we presuppose that this structure (as a structure of a molecule) is real and objectively existing. Is this really the case? Molecules are afterall belonging to an invisible domain, to which the concept of structure does perhaps not apply. Let us think about it for a while, before actually dealing with molecules as small Totalities.
Molecules are submicroscopical entities which cannot be directly observed (Even actual observation by means of a tunneling microscope is a very indirect one).
The structure of a molecule can, at first sight, be considered as a chemically stable configuration of atomic nuclei associated with an electron cloud, i.e. held together by shared electrons.
So we have to do with quantum particles.
And because of the quantum mechanical particle-wave dualism those particles are not completely localizable. So can Quantum Mechanics respect the chemists' discovery that molecules have a structure corresponding to fixed relative nuclear positions, and, consequently, a shape? Is molecular structure just a convention, or is it nevertheless real?
This question is posed and answered by Del RE, G., in an article called Ontological Status of Molecular Structure, published in HYLE - An International Journal for the Philosophy of Chemistry, Vol. 4 (1998), No. 2, pp. 81-103 (also available on the Internet).
His conclusion is that molecular structure does indeed exist.
The structure of submicroscopic entities can only be apprehended by analogy through the mediation of a macroscopic model, to which the notion of structure properly applies, i.e. structure is an analogous concept in Aristotle's sense. It's primary instance is the structure of macroscopic objects. Certain features that are not present in the model should be added when necessary (For quantum mechanical entities, for example, this means resorting to the double analogy : such an entity is a particle and a wave - which is not compatible with how things are at the macroscopic level).
For molecules this means that we have to imagine their structure according to a ball-and-spring model. Here the balls represent atoms (or atomic nuclei for that matter) and the springs represent bonds. These bonds can vibrate by being periodically stretched (BALL, 1994, Designing the Molecular World).
It turns out that the assumption of a structure in molecules (i.e. a geometrical configuration, and not just a topological one - relating only to connections) is in full agreement with experience in Chemistry, especially in that of designing new molecules.
In considering all this, Del RE distinguishes between the following (types of) entities :
R2 entities : entities that are only indirectly observable by means of inference.
FC entities : first class entities, i.e. subsistent entities.
SC entities : second class entities, i.e. non-subsistent entities, like property and structure.
Del RE then argues that (concerning first class and second class R2 entities)
"it is not the mathematics of quantum mechanics that determines what exists and what does not exist in the world of FC and SC R2 entities, but their experimental observability."
But observability of an object requires a long enough lifetime (of that object) for it to be observable. And this means in fact that the object should be stable enough for it to exist.
Of course we must admit that with all this some arbitrarity creeps in, but this is unavoidable. After all, in our investigation we have established a gradualness in Being all along.
Del RE states that the lifetime of the individual molecules must be longer by a few orders of magnitude than the mean collision time (in which short-living states can be formed) : a couple of picoseconds, 10-12 seconds, for ammonia in the vacuum at room temperature.
This means that the states of a molecule (its groundstate and its energetically excited states) are quasi stationary states which will not go into states, corresponding to other structures, within a few picoseconds.
The relation of Quantum Mechanics and the reality of molecular structure is summed up by a theorem (later more properly called an approximation) found by BORN and OPPENHEIMER :
Theorem : In the frame of Quantum Mechanics the atomic nuclei of a molecule can be treated as classical particles practically at rest as far as the motions of its electrons are concerned.
Corollary : Quantum Mechanics is not in conflict with the chemists' model of a molecule as a rigid framework of nuclei held together by shared electrons.
This is so because the nuclear motions are much slower than those of electrons in equivalent force fields. The displacements of the atoms from their equilibrium positions are very small with respect to the bond distances.
That the theorem was later viewed as an approximation is because of special quantum effects, vibronic coupling, particularly in the case of excited states. But vibronic coupling only concerns transitions between two structures (Del RE, p. 10 of the Internet version of his article).
So Del RE concludes that molecular structure and the rules of directed valency (number of possible bonds for atomic species) are facts of Nature, belonging to the complexity level where the 'elementary objects' (building blocks) are the atoms of the periodic table (which is a classification of atomic species).
But such a difficult issue like the structure of molecules, cannot of course be quickly settled once and for all.
As remarked by Del RE, his discussion is only a first exploration, which should be followed by quite a subtle and intricate technical discussion.
Now we shall discuss the formation of some molecules, namely the following :
In fact we only consider Hydrogen and Carbon, but with respect to that consideration the Elements Helium and Neon are, concerning stable states, also important. The other Elements from the following list are merely meant as illustration with respect to the increasing saturation of the outer electron shell.
The electron configurations of the above mentioned atomic species are as follows (if your browser does not support images then click here ) :
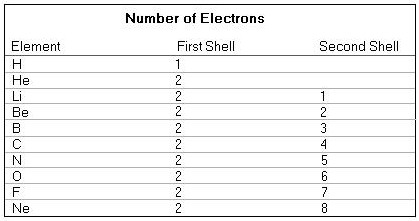
The first shell is saturated (i.e. totally filled) when it contains two electrons.
The second shell is saturated when it contains eight electrons. When there are more shells, then all shells up to the last (= outer) one (but this one not included) are saturated. This outer shell sometimes (i.e. in the case of some elements) is saturated, sometimes not. For an atom the most stable state means that the outer shell is saturated. This is, for example, the case with Helium (He) and Neon (Ne). That is why these gases are totally inert, they do not 'want' to change anymore ("To change " here means that the outer shell takes in or gives up one or more electrons. But because in such a process -- taking place in reality -- the number of protons in the nucleus remains the same, the species of atom also remains the same.). In order to obtain more stability, atoms, having an outer shell which is not saturated, try to give up electrons from the outer shell to another (species of) atom, or take in electrons from another (species of) atom, or try to obtain one or more pairs of electrons in common with other atoms. And all these cases result in obtaining a saturated outer shell.
Giving up or gaining of electrons gives rise to ions, these are therefore electrically charged because a difference has been generated between the amount of positive charge in the atomic nucleus and the amount of negative charge of the area surrounding the atomic nucleus. The common possession of pairs of electrons with other atoms gives rise to molecules.
These ions and molecules are entities which are more stable than the relevant atoms. A transition from atoms to molecules (which, it is true, in most cases needs a small energy boost), to which we, first of all, confine ourselves, can, provided that some external conditions are satisfied, proceed spontaneously. Because of the lower energy state of the generated molecule energy is given off into the environment. When the situation is energetically the other way round, energy must be supplied, and certain conditions must be such that the reaction does not reverse spontaneously.
This is possible.
From all this it is clear that the chemical properties of an (species of) atom are determined almost entirely by the condition of the 'outer' shell, i.e. by the configuration of the electrons in the highest energy level.
Until now we considered the distribution of the electrons among the shells. It remains to consider in what way the electrons are distributed within each shell. Only then we will obtain an adequate picture of the state of affairs of the area around the atomic nucleus. But this picture can be really adequate only when we abandon the image of an electron as a particle which performs revolutions around the nucleus.
Every material particle, big or small, shows, according to Quantum Mechanics, a Wave-Particle Duality. This means that such a 'particle' (i.e. the same individual particle) sometimes behaves like a (continuous) wave, somtimes as a (discrete) particle. But this phenomenon becomes significant only in the case of very small entities. The electron is effectively the biggest particle for which the wave-particle duality must be taken into consideration. And this determines the behavior of atoms, especially the way they can form bonds with each other resulting in molecules. The wave-like properties of complete atoms or molecules can be ignored for almost all practical purposes.
An electron in an atom can be most appropriately imagined as a diffuse cloud spreading itself out over almost the whole atom. Such a cloud, corresponding with a single electron, is at some locations denser than at other locations. When we still think, for a moment, about an electron as a particle, then we could say that the chance to find the particle (electron) is greatest in the denser regions of the cloud. But after this it is best to again forget this particle-image and interpreting the diffuse cloud as the 'real' electron. This diffuse cloud -- (sometimes only) representing one electron -- is in fact something like a ' standing wave ' around the atomic nucleus. Electrons of an atom are standing waves, trapped in the electrical potential field of the atomic nucleus. Because the image of an electron as a cloud is still a little vague we must specify it a little more.
The electrons are, as has been said, divided over shells. These shells should not be taken too litterally, but should be understood as energy levels . More accurately expressed : shells, but not shells alone, determine the energy levels. The division of electrons within an energy level implies a location of electrons in the form of the clouds mentioned. These clouds are called atomic orbitals . An atomic orbital is a cloud with a determined form and orientation, and can maximally accommodate two electrons. When such an orbital contains two electrons then those two electrons are not in the same state, but each of them in a different state. This state is called the spin of the electron. Electron-spin does not at all show any similarity with the rotation (spinning) of a top, but is an abstract state of the electron. Two spin-states are possible, up and down. When there are two electrons in an orbital then one of them has a spin up and the other a spin down. An orbital with two such electrons represents the most stable state. Just like the atom strives for a totally saturated outer shell, because this is a very stable state, the atom also strives for having two such paired electrons in every orbital (in the relevant shell) permitted by the Schrödinger Wave Equation. These two electrons are waves which 'mix' themselves up in such a way that a state of lowest energy results.
If we confine our discussion to the lighter elements (i.e. the lighter atomic species) then we find two main types of orbitals. In the lowest energy levels we find spherical orbitals (with the atomic nucleus in the center), and a little higher up on the energy ladder we find dumbbell-shaped orbitals (with the atomic nucleus in the ' waist '). The spherical orbitals are called s-orbitals, and the dumbbell-shaped orbitals are called p-orbitals.
We just said that the dumbbell-shaped orbitals appear at a next higher energy level. This is true for all chemical elements except Hydrogen. Here the energy of the electron levels depends only on the ' shell number ' (meaning in which shell the hydrogen electron is situated), wich implies that in Hydrogen the s-orbital of the second shell (= the 2s-orbital) lies in the same energy level as the p-orbital of the second shell (= the 2p-orbital). In all other elements the s- and p-orbitals lie in different energy levels. The first shell has (in all the elements) only a s-orbital (= the 1s-orbital). When energy is supplied to the atom, their electrons, also the one electron of the Hydrogen atom, can 'jump' from one energy level to another.
(BALL, Ph., 1994, Designing the Molecular World, p. 24, fig. 1.7)
Because the p-orbitals can differ in orientation, three types of p-orbitals are possible, namely px-orbitals, which are oriented along the X-axis of the 3-dimensional cartesian coordinate system, the py-orbitals, which are oriented along the Y-axis, and the pz-orbitals, which are oriented along the Z-axis (consequently posited vertically with respect to the other two).
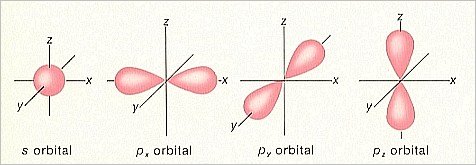
Figure 1. Shapes of s and p orbitals.
(After MOORE, J. & BARTON, Th., 1978, Organic Chemistry : An Overview )
By means of a number in front of the " s " of " s-orbital ", and in front of the "p" of " p-orbital ", we can denote the shell (energy level) to which the relevant orbital belongs. With a number as superscript we can denote the number of electrons in the relevant orbital.
The innermost shell always contains an s-orbital only, and in all cases of the existence of more shells containing electrons, this s-orbital consists of two electrons (this is the maximum number of electrons, not only for the orbital, but also for the first shell). Thus we can denote this s-orbital as : 1s2. Now the Schrödinger Wave Equation demands (i.e. predicts) the following state of affairs at the next (higher) energy level (the next shell) :
First of all there is again an s-orbital, which can be written as 2s2, but along with this one we find three other standing-wave patterns, with almost the same energy as the electrons in the just mentioned s-orbital, the px, py and pz orbitals, which, as has been said, are dumbbell-shaped, posited perpendicular to each other. Thus the second shell contains four orbitals : 2s2, 2px2, 2py2 and 2pz2. And when each orbital of this shell has (received) the maximum number of two electrons -- as indicated in the notation just given -- then the saturated second shell contains eight electrons.
This state of affairs becomes still more complicated at higher energy levels (thus -- in this context -- in cases of heavier atoms (atomic species)). But the quantum mechanical Wave Equation exactly predicts how many electrons fit in each shell. Also the form and orientation of the orbitals is predicted by the mathematics of the Quantum Theory.
Having this knowledge, it is now possible to precisely set out what the covalent chemical bond exactly is, and this means in what way the first Totalities (molecules) are formed from atoms.
H+H becomes H--H (= H2)
A covalent bond between two atoms is formed by an overlap of two atomic orbitals (one from each atom) giving rise to a molecular orbital. The two atomic orbitals each contain one electron which is a less stable state. The resulting molecular orbital now contains two electrons (these become, as a pair, a common possession of the two atoms), and this is a stable state. Each hydrogen atom has an 1s-orbital, containing one electron. At the formation of the hydrogen molecule from two atoms of hydrogen these orbitals overlap and now form one molecular orbital with two electrons. Such a bonding molecular orbital now comprises both hydrogen atoms, it has a cylindrical symmetry, and is called a sigma-bond.
But things are a little more complicated than this : A rigorous quantum mechanical description of the bonding in the H2 molecule demands that the total number of orbitals must be conserved. We started with two atomic orbitals, so we must end up with two molecular orbitals. One such orbital we have just described, it is called the bonding orbital in which the electron pair resides. The other molecular orbital is empty, it does not contain any electron. The energy of this empty orbital, i.e. the energy of an electron, if it were situated in -- or boosted up to -- this orbital, is higher, than the energy in the atomic orbitals. Putting electrons into this orbital will weaken the bond, since the total energy is then greater than that when electrons occupy just the molecular bonding orbital. The orbital is therefore called an antibonding orbital (BALL, 1994, op. cit.). See next Figure.
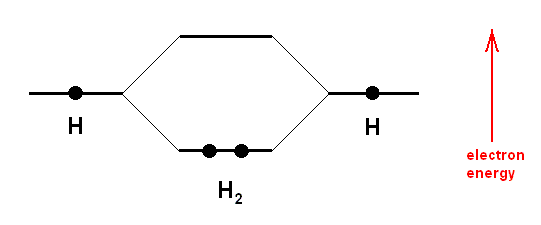
Above Diagram : A covalent bond is formed when atoms share electrons. In effect, the shared electrons can orbit around both nuclei in "molecular" obitals. More precisely, there is s significant probability of finding these electrons around either of the nuclei. In the hydrogen molecule (H2) the two 1s orbitals on the individual atoms overlap to form an elongated molecular orbital encompassing both nuclei, with an energy lower than that of the constituent atomic orbitals. At the same time, an empty "antibonding" molecular orbital is created at a higher energy. The lowering of the electrons' total energy in forming the molecular orbitals is what holds the molecule together.
Because H2 is a more stable configuration than two (freely existing) hydrogen atoms, energy is released to the environment during the formation of H2 from two hydrogen atoms. This is called the bonding energy. The same amount of energy is required to break the bond (here the covalent bond between two hydrogen atoms) up again, in order to get back again the two hydrogen atoms from a hydrogen molecule.
So we now have described the formation of the smallest molecular Totality, namely a Hydrogen molecule.
Each hydrogen atom in itself is -- considered after the fact -- a result of the gathering of a proton and an electron. This whole is in the most stable state when the electron finds itself in a spherical orbital, a 1s-orbital. This state of affairs is dictated by the Schrödinger Wave Equation. But atoms show a strong propensity to saturate their outer electron shell, and for a hydrogen atom this means that its (only) shell will strive to obtain two electrons (In the case of representatives of the other atomic species, all (except Helium) having more than one shell, the second shell is saturated not until it contains eight electrons ). The hydrogen atom can achieve this by, for example, entering into a covalent bond with another hydrogen atom. The resulting hydrogen molecule is, according to the mathematics of Quantum Mechanics, more stable than the two freely existing atoms. A H2 molecule is accordingly the stable end-state of the interaction process of the two hydrogen atoms. Expressed alternatively, the dynamical system, consisting of two system elements, resulted (under appropriate external conditions) in the generation of a real intrinsical, but still microscopical, stable Totality, a new being. The dynamical law which has operated in this case is immanent in the two hydrogen atoms, and can be understood from the quantum math. This quantum math describes the energy states of atoms and molecules. And every system strives -- when not interfered with -- for a lowest energy state, because that guarantees the highest stability.
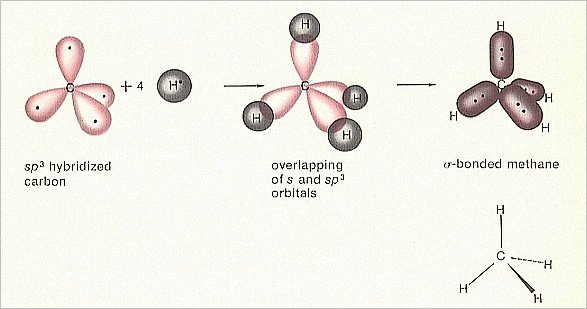
Figure 2. Orbital construction of Methane
(After MOORE & BARTON, 1978)
Also in this case (of Methane) the configuration is more stable than the case of four free hydrogen atoms and a carbon atom before the bonding took place. So also here we can speak of a dynamical system, consisting of five system elements, namely four hydrogen atoms and a carbon atom. This system generates a stable Totality -- a Methane molecule -- when certain external conditions are satisfied. Expressed in another way : When these external conditions prevail, then the dynamical law for (the generation of) Methane (i.e. the generation of a Methane molecule) will ' start to operate ', and, consequently, the Totality, the Methane molecule, will appear. This dynamical law can be understood on the basis of the quantum math, which predicts the energy states.
With the help of the theory of orbitals we can show the structure of the carbon--carbon bonds (of course (the explanation of) this bond is also based on the quantum math).
When we have a sp3 hybridized carbon atom, thus with four sp3 orbitals, then three of them can overlap with, say, hydrogen (Here we expound the formation of the Ethane molecule). In this way we obtain a so-called Methyl radical, CH3. This still contains a left-over sp3 orbital. We now can couple two such methyl radicals together by letting these left-over sp3 orbitals overlap each other, resulting accordingly in a sigma-bond between the two carbon atoms ( The bonds with the hydrogen atoms also are sigma-bonds).
What we obtain is an Ethane molecule, H3CCH3 (= C2H6).
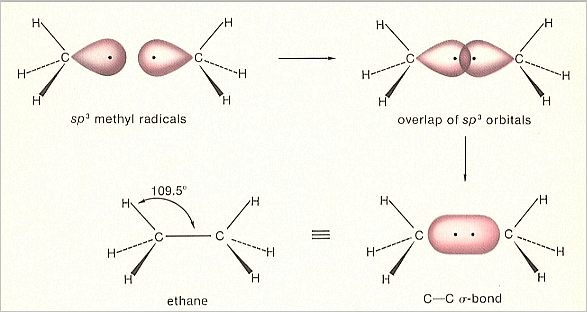
Figure 3. Orbital construction of Ethane
(After MOORE & BARTON, 1978)
Also in this case a more stable (with respect to the free hydrogen atoms and free carbon atoms) Totality is generated, an Ethane molecule, in which all atoms possess a totally saturated outer electronshell, because of having electron pairs in common. Moreover each orbital contains two electrons and so it is stable too.
The dynamical system, with system elements H, H, H, H, H, H, C and C, generated the Totality H3CCH3, or, denoted in a more elaborated fashion :
H
HCH
HCH
H
It generated an Ethane molecule.
Carbon atoms can also form double bonds with each other. Such a covalent double bond has a particular structure, which we shall explain with the (help of the) formation of an Ethylene molecule.
When we have sp2 hybridized carbon (which as such is generated in the case of certain bondings), then we have three sp2 hybrid orbitals. And a p-orbital was still left over, oriented perpendicular to the plane of the three sp2orbitals. When we now couple two hydrogen atoms to two (out of the three) sp2 orbitals of the carbon atom (consequently everytime an overlap of an 1s-orbital -- containing one electron -- of hydrogen, with an sp2 orbital -- containing one electron), then we obtain a H2C unit in which there are still two orbitals left, having both only one electron, namely an sp2 orbital and the left-over p-orbital.
We can now couple two such units together by letting their sp2 orbitals (which have not participated in the bonding with hydrogen) overlap (resulting also in this case in a maximally filled -- with two electrons -- molecular orbital). Consequently the carbon atoms will then be bonded to each other with a sigma-bond. But both H2C units also still have the mentioned left-over p-orbital, i.e. two p-orbitals perpendicular to the other orbitals. These can overlap sideways with each other resulting in a stable molecular orbital. But because this molecular orbital is perpendicular to the remaining orbitals, the bonding is still, it is true, a covalent one -- because it is based on a common possession of one (or more) electron-pairs -- but is of a different type (within the covalent bonds) than the sigma-bond. Such a bond is called
a pi-bond.
While the bonding-orbital in the case of a sigma-bond lies in the axis (conceptually) connecting the two bonded atoms, it lies in the case of a pi-bond above and below (but not in) that axis. The resulting molecule is an Ethylene molecule, H2C==CH2. It reveals the following pattern :
H H
C
C
H H
It is a flat molecule with the sigma-bond between the two C-atoms lying in that plane (The same is the case with the sigma-bonds with the four hydrogen atoms) and the pi-bond between these two C-atoms lying above and below that plane.
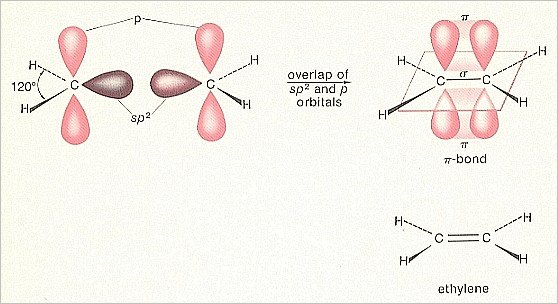
Figure 4. Construction of the double bond
(After MOORE & BARTON, 1978)
Also in this case a stable Totality has been formed from the system elements
H, H, H, H, C and C.
In a comparable manner also the generation of a triple bond between two carbon atoms is possible. When they saturate themselves subsequently with hydrogen then we have Acetylene, HCCH, where the C-atoms are bonded with each other by means of three bonds.
As to the double bond between carbon atoms, we must add the following : The structure of the benzene molecule consists of a closed ring of six carbon atoms and is satisfied with six hydrogen atoms (one to each carbon atom), C6H6. The six bonds between the six carbon atoms of the benzene ring seem to be : three single and and three double bonds : As we go around the ring, we find a single bond, then a double bond, etc., meaning that, when going around the ring we have a static alternation between the single and double bond between the carbon atoms. Of this there are, of course, two possible arrangements, which become evident when we, for example, replace two adjacent hydrogen atoms of the benzene molecule by chlorine (obtaining dichlorobenzene). Then one might expect two distinct structures for the molecule, one with a double bond between two chlorine-bearing carbons, and the other with a single bond in this position. Experimental studies insist, however, that there is only one kind of dichlorobenzene. And this means that the six bonds of the benzene ring are equivalent. And this equivalence may be expressed either by saying that the actual benzene ring is a resonance hybrid, i.e. oscillating back and forth between the two possible arrangements of single and double bonds, or that, rather than flipping in this manner, the pi-bonds [each of which together with the sigma-bond forming a double bond] of the molecule become smeared out into two continuous electron clouds running around the ring above and below. The electrons in these molecular orbitals can move readily from atom to atom all around the loop : they are said to be delocalized.
For us, in comparing organisms with inorganisms, the carbon atom (C) is one of the most important atoms.
Carbon has a valence of four - it can form four bonds with other atoms. Because the most stable configuration for an atom is a filled outer shell of eight electrons, this is normally the largest valence any atom can have. With less than four electrons in its outer shell, an atom will tend to form molecules in which the electrons (up to three of them) are in effect given up to its partners, laying bare the filled shell beneath. With five, six or seven electrons in an outer shell, an atom has room for only three, two, or one partners. Carbon has four electrons, each unpaired in an orbital, ready and willing to latch on to electrons from other atoms. There are, of course, other atoms in a simular configuration. Carbon has atomic number six, two electrons in its innermost shell and four in the chemically active shell. Silicon (Si) has atomic number 14, with its electrons in a 2 : 8 : 4 configuration. Like carbon, it forms four bonds at a time. But, because the four key electrons are in a higher energy state ('farther out from the nucleus' on the old picture) the bonds are weaker.
But as ever with nice simple rules there are exceptions. Phosphorus (P), for example, has atomic number 15 and five electrons in its outermost occupied shell. It is capable of utilising each of the five electrons to make a total of five bonds at a time. The easiest way to think of this is as four covalent bonds involving shared electron pairs, as in carbon, plus one ionic bond involving the transfer of an electron from the phosphorus to its partner. Since each of the five bonds is the same as each of the others, however, this image requires imagining each of the bonds to be 80 percent covalent and 20 percent ionic in character. This is very much in accordance with the new understanding of quantum chemistry developed in the 1930s.
These, then, are the possible types of chemical bonds in molecules : the covalent bond, the electrovalent (ionic) bond, the hydrogen bond, and the dative bond. As to the first two, there is not, in fact, any clearcut dividing line between compounds that are purely ionic in nature and thsose that are purely covalent. Some are more ionic in nature, others seem predominantly covalent, with all shades of grey in between. All bonds can be regarded as a mixture, a blend of the two types. Even hydrogen can be thought of as making ionic bonds. If one atom gave up its electron to the other, we should have a molecule H+ H-. If the exchange went the other way around, we would have H- H+. The covalent sharing of the two electrons can be thought of as very rapid switching between these two states, with first one atom and then the other laying claim to both electrons, and the two atoms being held together by the electrostatic forces. This idea of oscillating between different states, or resonance, was at the heart of Pauling's work in the late 1920s, the work which put the theory of covalent bonding on a secure mathematical footing within the framework of quantum theory. As far as molecular biology is concerned, the covalent bond is the bond. Purely ionic bonds like those in sodium chloride play no part in forming the molecules that are important to life, although resonance is important, and weaker electrostatic forces are very important in determining the exact shape of large biomolecules.
H H H H
H C C C C H
H H H H
and
H
H H C H H
H C C C H
H H H
Thus a same collection of four C-atoms and ten H-atoms can give two different patterns of those same atoms. These are two different -- concerning content -- Totalities, but having the same empirical formula C4H10. They are called isomers .
When the chain lenght increases, the number of isomers grows very rapidly.
When the carbon is bonded not only with hydrogen but also with other chemical elements, for instance with oxygen (O) then there are even more possibilities for isomerism. Let's look to two compounds with the formula C2H6O, where one of them contains two C--O bonds and the other a C--O bond and a O--H bond. These isomers possess very different chemical properties, one of them is an unreactive ether and the other is a very reactive alcohol:
H H
H C O C H
H H
Dimethylether
H
H C H
H C H
O
H
Ethylalcohol
The ether is almost totally insoluble in water, while the alcohol is infinitely soluble in water.
The fact that the extremities of a carbon chain can bond with each other, resulting in a cyclic structure, offers new possibilities for isomerism.
The formula C5H10 can represent a 5-carbon chain, straight or branched, with a double bond, or a ring structure with single bonds only.
A very interesting recently discovered (and synthesized) family of molecules are the Fullerenes. These are molecules consisting solely of carbon atoms. Until this discovery only two types of carbon 'molecules' were known : Diamond and Graphite. Both are crystalline structures consisting of an indefinite number of carbon atoms, arranged in periodic arrays. So these are crystals -- and so not molecules in the strict sense.
But the recently discovered carbon structures are real molecules, because in them a definite number of individual carbon atoms is involved. Such a molecule consists of carbon atoms arranged, not in a periodic way, but forming a closed cage of relatively few atoms.
The first discovered (in the 1980's) Fullerene is a molecular cage consisting of 60 carbon atoms. The cage is a closed hollow ball of 60 carbon atoms arranged in the form of a soccer ball. This ball is in fact a polyhedron consisting of twelve pentagons and twenty hexagons, just like the patches of a soccer ball. The carbon atoms reside at the vertices (one atom at each vertex). Because in such a structure each atom is connected to three others, one of those three bonds must be a double bond, making four bonds for each carbon atom (so no bonds are unsatisfied dangling bonds). The inspiration that the new molecule should have this cage-like structure consisting of polygons, came from the structure of the geodesic dome at the Montreal Expo of 1967, designed by the American architect Richard Buckminster Fuller. So the new molecule was christined buckminsterfullerene.
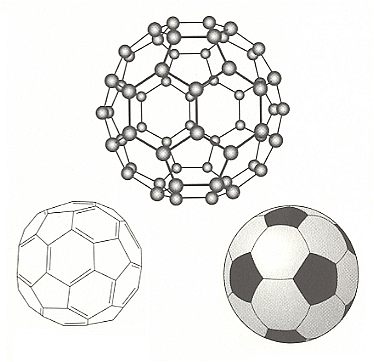
Structure of Buckminsterfullerene
Top : The structure of the sixty-carbon-atom cluster, called buckminsterfullerene.
Left : The pattern of single and double bonds which allows all of the atoms to form four bonds.
Right : The pattern of hexagons and pentagons in this highly symmetrical shape is the same as that in a soccer ball.
Each carbon atom in the cage is equivalent.
(After BALL, 1994)
Because of mathematical reasons such closed molecular cages can only be formed when, in addition to a number of hexagons, there are precisely twelve pentagons present in the structure ( NOTE 4 ). A second restriction is that the pentagons should not be located adjacent to each other -- this would give rise to an unstable bonding pattern, which would rapidly rearrange. All pentagons must be isolated from one another. This clearly is a chemical restriction. For C60 (buckminsterfullerene) there are 1812 possible ways of arranging the pentagonal and hexagonal rings, but only one in which no pentagons are adjacent. So C60 has no isomers.
But also larger fullerenes have become known, and these do have isomers. But their number is limited because of the restriction mentioned. So C76 has just two, it seems, and C78 perhaps eight or so. The giant fullerenes C120, C240 and C540 are expected to have some particularly symmetrical isomers, but these molecules haven't yet been isolated in sufficient quantities to put this to the test.
So it is clear from the first examples that isomers, having, accordingly, a same empirical formula (= a same number and type of atoms), can strongly differ from each other. Such a group of isomers represents a collection of possible combinations (configurations) of a same number and type of atoms.
Seen after the fact it is clear that the same dynamical systems (in which " the same " means : consisting of a same number and type of system elements) can result in the generation of different (with respect to content) Totalities. This implies that those dynamical systems turn out to be not the same, with respect to content, only their pool of elements was the same. It follows that the Dynamical Law for such a Totality (generated thing) is not equivalent to the complete collection of system elements, because in that case only one dynamical law would be possible. In the case of isomerism many Dynamical Laws are possible, relating to a same pool of system elements. And in the case of the generation of the several Fullerene species we see that a large enough collection of specifically the same elements can give rise to several possible species of Totality. Now it is also clear that the nature of such a dynamical law (and, in general, every dynamical law) is abstract.
Let's give a brief exposition about the seat of a dynamical law, and how the above mentioned phenomena are thought to be possible.
(See for more details the Essay on Dynamical Systems ).
The Dynamical Law of a dynamical system must reside in some way in the system elements, more precisely in some of the properties of the system elements.
The actually existing properties relating to each freely existing system element (i.e. as such distinguished from the Essence of such a system element) either are actual and constant structural configurations, or an interaction (result) with external factors. These last mentioned actually existing properties of a system element are as such dependent on the outside world. In this context the " outside world " not only comprises the remaining system elements but also the other entities not belonging to the dynamical system as such (not being system elements). Abiding in all these actually existing properties (including the constant properties) of all those system elements is the Dynamical Law relating to the generation of a certain Totality (a uniform thing), predetermined by this law. Altered external conditions result in a change of some of these properties (i.e. resulting in an exchange of some properties) implying that a part of the actually existing properties is now different, and this new garnish of actually existing properties of system elements now harbours a new (i.e. different with respect to content) Dynamical Law, resulting in the generation of a different, with respect to content, Totality.
Of course the effects of environmental changes on (the alternation of) actually existing (i.e. actually being present) properties of system elements are partially rooted in the nature of those system elements themselves (i.e. in certain constant structures in each of those system elements).
Molecules are Totalities, each consisting of a definite and fixed number and proportion of individual atoms [ in contrast to crystals, where the proportion is, it is true, also constant (except in the case of mixed crystals, that constitute a special problem, discussed earlier), but where the number of individual atoms participating in the crystal structure is not fixed : a single crystal consists of the periodic stacking of microscopic units in three directions, resulting in the fact that its size is not fixed ]. A molecule consists of a definite number of parts giving rise to a definite shape and size. Such a structure we call tectological (in contrast to that of single crystals). This tectological structure we also encounter in certain twinned crystals, that can be considered as consisting of several single crystals grown together in a regular and repeatable way, according to one or another twin law. And almost all organisms, and their parts, show this structure too, which allows them to have certain definite imaginary body axes, that, together with the quality of their poles (namely being homopolar or heteropolar) allow for their stereometric basic form to be determined. On the basis of this we can classify such organisms as Axonia, while the few organisms that do not admit of such a stereometric basic form to be determined, can be called Anaxonia (The Axonia can be further classified into Homaxonia, Polyaxonia, Monaxonia, Stauraxonia and Spiraxonia, depending on the differentiation and nature of their axes and poles).
On the second (part of this) website, accessible by clicking on the last entry of the contents frame Continuation of this Series, we have laid down the complete theories about the tectological structure (TECTOLOGY) and stereometric basic form (PROMORPHOLOGY) in organisms.
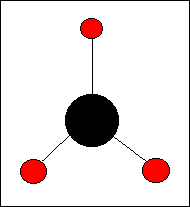
Many molecules, especially the smaller ones, are Axonia, they all have a definite stereometric basic form. A nice example is the Methane molecule, CH4, that has the shape of a regular tetrahedron. And of course such a form is one of the effects of the relevant Dynamical Law.
In all the above we have demonstrated how the very small Totalities generally look like, and in what way their structure is dictated by energy-states.
So in this Essay we have learned that the Chemical Bond is crucial for the possibility of the formation of whatever Totality above the atomic level.
In the above REMARK we spoke of the possible uni-molecularity of organisms (Unimol), a view that considers every individual organism to be one single giant molecule embedded in an aquous serum-like support medium. We have worked out this in Sixth Part of Website. And again we here give the relevant LINKS : The Unimol view of organisms is extensively discussed from part XVg onwards in Sixth Part of Website (if the reader wants to directly access the mentioned part XVg (of Sixth Part of Website), he or she should click HERE.
back to homepage