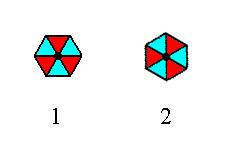
back to homepage
The symmetry of regular 2-D arrays of repeated motifs (continued)
The next motif we're going to insert in a 2-D hexagonal lattice has the same point symmetry as the one we used for the exposition of Plane Group P3m1 in the previous Part. But with respect to the connecting lines of the net our new motif is oriented differently : It is rotated 300 with respect to the one used earlier. See Figure 1.
Figure 1.
(1). Orientation of the 3m motif, compatible with the Plane Group P3m1 (discussed in Part Five).
(2). Orientation of the 3m motif, compatible with the Plane Group P31m.
Placing two-dimensional motifs with 3m symmetry into a (primitive) hexagonal net (2-D hexagonal lattice), such that the orientation of these motifs differs by 300 from that of the motifs of the Plane Group P3m1 (discussed in the previous Part), yields a periodic pattern representing Plane Group P31m. See Figure 1a.
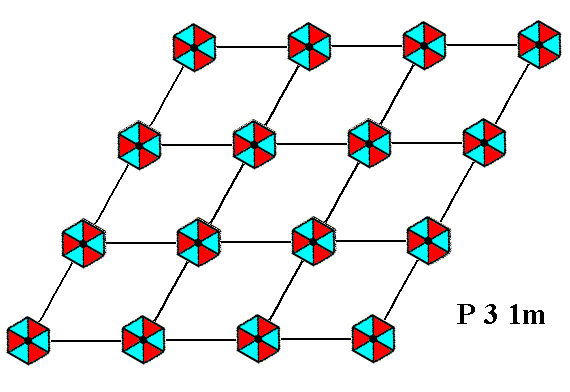
Figure 1a. When motifs, having point symmetry 3m (i.e. having a 3-fold rotation axis and three equivalent mirror lines), are inserted into a (primitive) hexagonal net, in the way (i.e. the orientation) shown, a pattern of repeated motifs will emerge that represents Plane Group P31m .
The symmetry of the motifs is indicated by their shape and by their coloration.
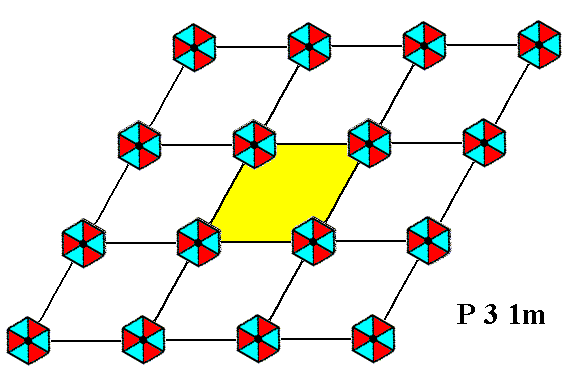
Figure 1b. A unit mesh is chosen (yellow). This unit mesh is primitive, and its point symmetry is m, i.e. the only symmetry element it possesses is a mirror line.
If the pattern representing Plane Group P31m is contracted such that all translations are eliminated, then we end up with a figure that has 3m symmetry. It is the translation-free residue of that Plane Group, and as such represents the Point Group to which that Plane Group belongs. See Figure 1c.
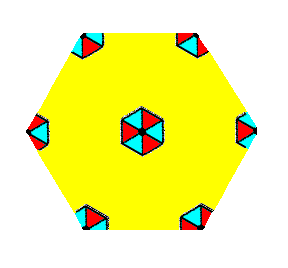
Figure 1c. The translation-free residue of the pattern -- representing Plane Group P31m -- of Figure 1a. The point symmetry of this residue is 3m , and as such it represents the Point Group 3m to which the present Plane Group belongs. The translation-free residue is at the same time the motif s.l. and tiles the 2-D plane completely.
The symmetry elements involved in a pattern representing Plane Group P31m are 3-fold rotation axes, mirror lines and glide lines. See Figures
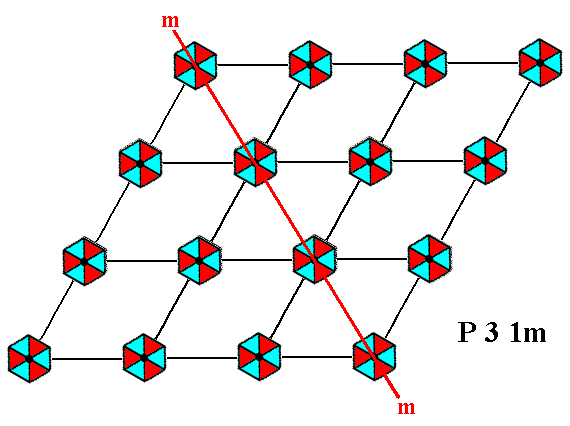
Figure 1d. A pattern representing Plane Group P31m has mirror lines. One of them is depicted here.
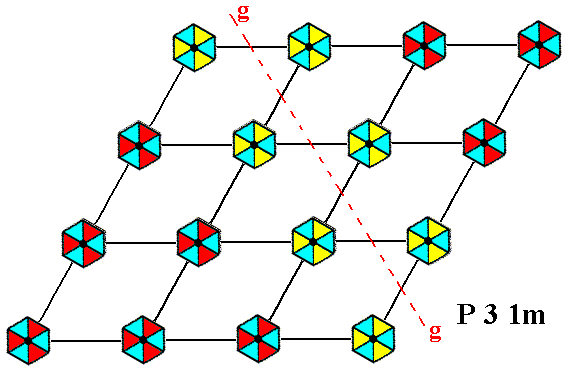
Figure 1e. A pattern representing Plane Group P31m has glide lines. One of them is depicted here.
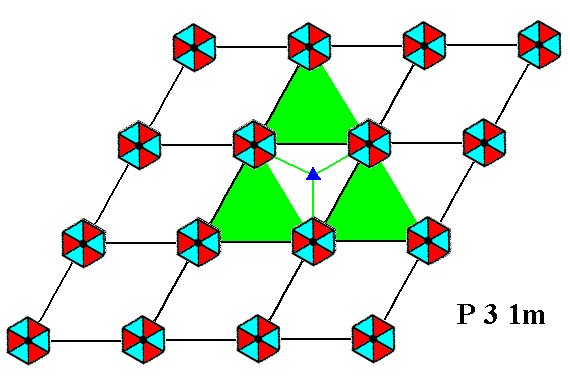
Figure 1f. A pattern representing Plane Group P31m has 3-fold rotation axes. One of them is depicted here.
The total symmetry content of the Plane Group P31m is given in the next Figure.
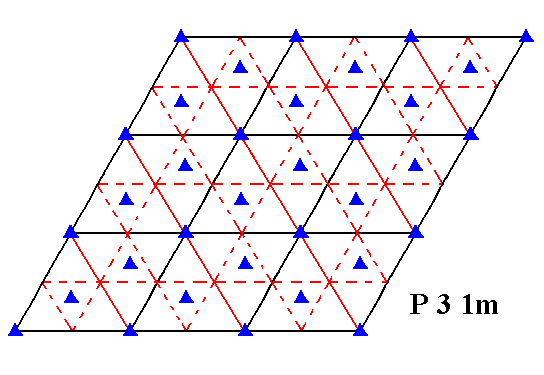
Figure 1g. Total symmetry content of Plane Group P31m.
Mirror lines are indicated by solid lines (red and black).
So we now have discussed the second and last Plane Group (P31m) belonging to the Class (Point Group) 3m.
Finally we have arrived at the last 2-D Crystal Class, namely 3. The only Plane Group that belongs to it is P3.
If we place motifs, having a point symmetry 3 (i.e. the only symmetry element each one of them has is a 3-fold rotation axis), in a hexagonal net, then we obtain a periodic pattern (of motifs) representing the Plane Group P3. See Figure 2.
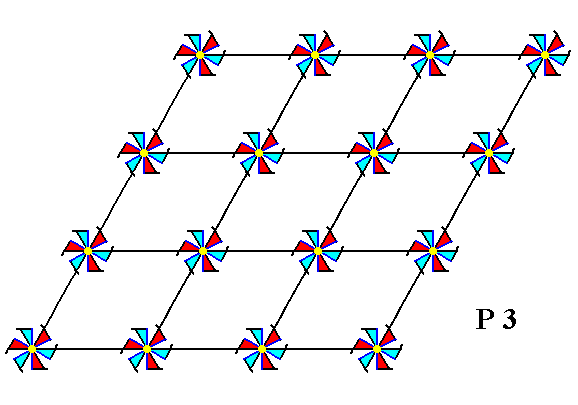
Figure 2. Arranging motifs with point symmetry 3 in a hexagonal 2-D lattice yields a pattern that represents Plane Group P3.
The symmetry of the motifs is indicated by their shape and by their coloration.
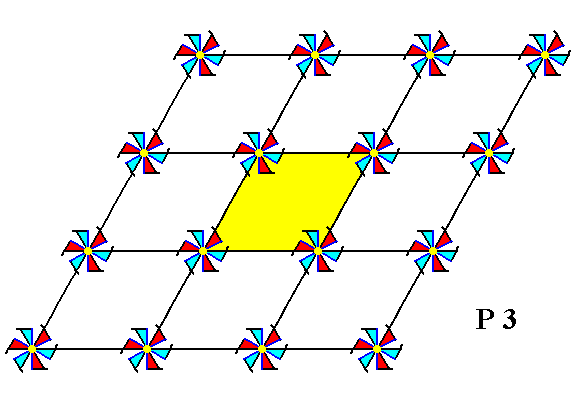
Figure 2a. A unit mesh is chosen (yellow), it is primitive and has point symmetry 1, i.e. it has no symmetry whatsoever.
If we contract the pattern of Figure 2, representing Plane Group P3, such that all translations are eliminated, then we end up with a figure having a point symmetry 3. This figure then represents the Point Group (Crystal Class) 3 to which that Plane Group belongs. The figure is at the same time the motif s.l. of the pattern. It tiles the 2-D plane completely. See Figure 2b.
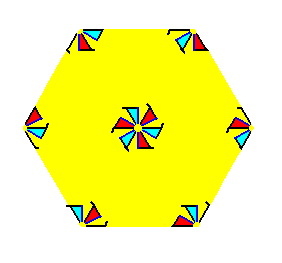
Figure 2b. Translation-free residue of the pattern of Figure 2. It represents the Point Group of the Plane Group P3.
The symmetry elements involved in a pattern representing Plane Group P3 are 3-fold rotation axes only. Through every node of the net there is such an axis, and a pair of them is situated in each mesh. See Figures 2c and 2d.
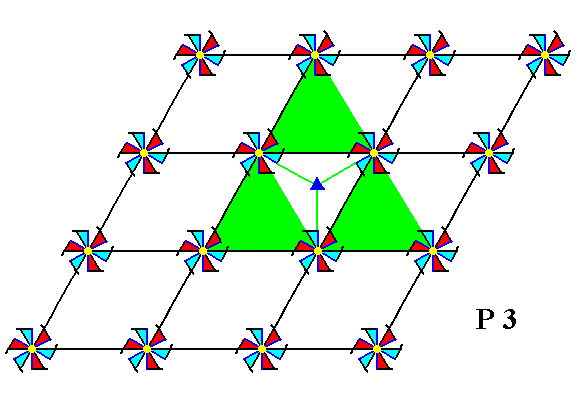
Figure 2c. A pattern representing Plane Group P3 has 3-fold rotation axes. One of them is shown (small blue solid triangle).
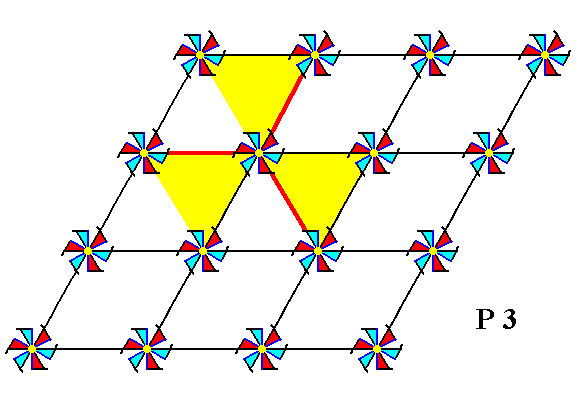
Figure 2d. A pattern representing Plane Group P3 has 3-fold rotation axes. One of them is indicated. It is situated at a node of the net.
The total symmetry content of the Plane Group P3 is given in the next Figure.
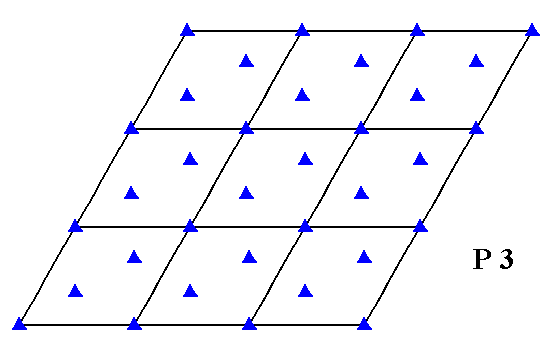
Figure 2e. Total symmetry content of the Plane Group P3.
There are no mirror lines and also no glide lines. The Plane Group only possesses 3-fold rotation axes.
This concludes our discussion of the planar Point Groups and Plane Groups of the 2-D Hexagonal Crystal System, and with it we conclude our exposition of the ten 2-D Point Groups and of the seventeen 2-D Plane Groups that belong to these Point Groups. In two dimensions only these 10 Point Groups and the 17 Plane Groups are possible, when we demand that the patterns, formed from objects (motifs), are periodic. The point symmetry of such an object (motif) must belong to one of the ten planar Point Groups.
In the next Part we will summarize our findings with respect to the 2-D plane.
To continue, click HERE for Part Seven.
back to homepage