The Symmetry of Two-dimensional Patterns

As prelude to the symmetry of three-dimensional crystals and organisms

Subpatterns and Subgroups Part II :
Antisymmetry Groups, Color-symmetry Groups
e-mail : 

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first  q, then  p, and then  a.
General Considerations, Antisymmetry Groups, Color Symmetry Groups
Classification of isometric groups acting on the Space E2

Before we will treat the Friezes (strip patterns) systematically in the next documents, we will, in the present document, say some more about the classification of two-dimensional patterns, in order to put those friezes into a broader context.
There are several fundamental types of spaces, one of which are the Euclidean spaces  En  to which we will limit ourselves. The superscript  n  denotes the dimension of such an Euclidean space. When  n = 0, the space is a point, i.e. the space  E0 . When  n = 1, we have a line, i.e. the space E1, when n = 2 we have a plane, i.e. the space  E2 . When  n = 3, we have our ordinary three-dimensional space  E3 .
A symmetry transformation (or, simply, a symmetry) with respect to a figure in a certain space (and thus symmetry in the geometric sense) is a transformation of that space onto itself, in such a way that that figure occupies the same patch of space as it did before the transformation, despite the fact that it has been rotated, reflected, etc. by this transformation, and thus despite the fact that some points of that figure changed their position.
A symmetry group -- here considering symmetry in the geometrical sense -- is a set of (geometric) symmetry transformations, together with a group operation, which is the successive application of two such transformations both belonging to that set. A symmetry transformation, and also any combination of such transformations (acting) on an euclidean space  En ,  associates to every point of that space another point of that same space, so we can say that such a symmetry group as a whole acts on that euclidean space  En .
There are three main types of symmetry transformations :

All three types are important for understanding two-dimensional patterns (periodic and non-periodic) including their isomorphic counterparts in three dimensions (as we see some of them in organisms and crystals). For example a regular polygon is isomorphic to its corresponding regular pyramid having this polygon as its base. The two-dimensional patterns are, in turn, instructive for an understanding of their non-isomorphic counterparts in three dimensions (some of which we also find in organisms and crystals). [Recall that two groups G and G' are isomorphic to each other, when they have the same abstract algebraic structure, which means that we can always set up a one-to-one correspondence between their respective elements, such that products are preserved]. Until now we only considered isometric symmetries. We will continue with them, while the other two will be considered later.
An isometric symmetry of a space En is a transformation  s  of that space such that for every two points P, Q of that space (P,Q) = (s(P),s(Q)), where (P,Q) denotes the length of the line segment defined by the points P, Q.  Or in other words, a transformation is an isometry if the distance between the images under that transformation is the same as the distance between the originals. All isometries of some space form a group.

Let us elaborate some more concepts.
A closed set (here we think of a set of geometric points) is -- informally -- a set with a definite boundary belonging to that set.
The closure  Cl(F)  of a set  F  is the smallest closed set containing that set, equal to the intersection of all closed sets containing  F .
The interior of a closed set  F ,  denoted by  int(F) ,  is -- informally -- this same set without its boundary.
The group of transformations  G  is discrete  if for each point  P  of the space in which the group  G  acts there is a positive distance  d = d(P)  such that no image of  P  (distinct from P) under an element of  G  is at a distance less than  d  from  P .
The set {S1, S2, S3, . . . , Sm} of elements of a discrete group  G  is called a set of generators of  G  if every element of the group can be expressed as a finite product of their powers (including negative powers and the power 1).
For a discrete group  G  it is possible to define a fundamental region of  G .
A fundamental region  F  is a figure which satisfies the following conditions :

The set of points  G(P) = {g(P) |  g element of G}, obtained from a point P by all transformations of the group  G ,  is called the orbit of  P  with respect to  G .  It is the set of points equivalent to point  P ,  or the transitivity class of  P ,  with respect to the group  G .  Analogously we can also define the orbit (or transitivity class) of any figure  f  with respect to the group  G  and denote it by  G(f) .
A point  P  which is invariant with respect to a transformation  s ,  i.e. a point for which
s(P) = P ,  is also called singular. A Figure  f  is invariant with respect to a transformation  s  if  s(f) = f .  A point  P  is a singular (invariant) point of a group  G  if it is a singular (invariant) point of all transformations of  G . A point which is not an invariant point of a transformation  s  is also called a point in general position with respect to the transformation  s .  A point is said to be a point in general position with respect to a group  G  of transformations, if it is in general position with respect to all the transformations of the group  G ,  i.e. if it is not an invariant point of any transformation of the group  G . For example, the singular (invariant) point of the symmetry group of Square (D4) is the center of the square. The points belonging to the square's mirror lines are the invariant points of the corresponding reflections (and not of the group). All other plane points, are the points in general position with respect to the symmetry group of Square.
If  Cl(F) is the closure of the fundamental region  F ,  the orbit G(Cl(F)) represents a tiling of the space on which the group  G  acts. A space tiling or tesselation is a countable family of closed sets T = {T1, T2, T3, .  .  . }  covering space without gaps or overlaps. T1, T2, T3, .  .  .  are the tiles of  T .
As the result of the action of the symmetry groups we have tile-transitive or isohedral tilings. Their tiles belong to the same class of transitivity (i.e. to the same orbit) G(Cl(F)), since for every two tiles of G(Cl(F)) there exists a transformation of group  G  which maps one tile onto the other. The tiles of such a tesselation do not necessarily have the same orientation.
A continuous set of points is any set of points which satisfies the axiom(s) of continuity. Every continuous set of points is a homeomorphic image of a line, i.e. in order to get such an image we may bend, fold or stretch such a line as we please provided we do not break it. A symmetry group  G  of the space  E2  is called fully continuous if the orbit G(P) of a point in general position P with respect to the group G satifies the following condition :

G(P) is the complete space on which G acts.

By the term continuous group of translations and rotations we mean that all translations along one line, i.e. shifts of any length along one or another line, all rotations about one (or another) center, are elements of such a group.
So the plane, i.e. the space E2, is a continuous symmetry group. All two-dimensional discrete patterns, periodic as well as non-periodic) are subgroups of this continuous two-dimensional symmetry group (with two independent translation vectors).

We are now ready to say something about the classification of isometric (distances invariant) symmetry groups that act on the space E2 (two-dimensional euclidean space, i.e. the ordinary plane). (Based on JABLAN, S., 2002, Symmetry, Ornament and Modularity, p. 15 and p. 21)
As the basis for the classification of all symmetry groups (not only isometric) three items were taken into consideration :

According to this, the so-called Bohm symbols are used for the categorization of the groups of isometries, similarity symmetry groups, and conformal symmetry groups.
For the groups of isometries the letter  G  is used (while for the similarity symmetry groups the letter S, and for the conformal symmetry groups the letter C is used -- the latter must not be confused with the symbol Cn for cyclic groups, which are isometries).
So the first part -- capital letter -- of the Bohm symbol denotes the overall symmetry group type (isometric, similarity, or conformal). The first subscript of the Bohm symbol denotes the maximal dimension of the space on which the group acts. The second and third subscripts, if present, denote the maximal dimensionality of subspaces that are invariant with respect to the groups falling under the given category.
For example, the symmetry group of Square,  D4  is a group of isometries, denoted by the symbol  G ,  it acts in the plane, i.e. in the two-dimensional space, denoted by the first subscript  2 ,  and possesses only one invariant point, i.e. the only subspace that is invariant with respect to that group is a space having 0 dimensions, denoted (in the Bohm symbol) by the second subscript  0 ,  so it belongs to the category  G20  -- the symmetry groups of rosettes.
On the other hand the group  P4mm  is has no invariant subspaces whatsoever, while it also acts on E2, and is a group of isometries, so it belongs to the category  G2  -- the symmetry groups of ornaments.
Further we have isometric groups acting on E2 with an invariant 1-dimensional subspace (line) and without invariant points (here the points move, i.e. are mapped onto each other in such a way that the images (image points) remain on the original line). These are the symmetry groups of friezes, denoted by  G21 .
If we have to do with groups that have several, i.e. more than one, invariant subspaces with respect to the given group, then the dimensionality of those subspaces is indicated in the Bohm symbol in the order that they include each other. So, for example, the last two subscripts (2, 1) of the symbol  G321  (the symmetry groups of bands) denote an invariant plane (included in the 3-dimensional (carrier) space, in which [invariant plane] no points are invariant) which includes an invariant line. The space that carries the pattern -- where the dimensionality of that space is indicated in the first subscript of the Bohm symbol -- is also invariant with respect to the group describing that pattern.

The groups of category  Gn  are called space groups, the groups of the category  Gn1  (where the second subscript is a one) the line groups, and the groups of the category  Gn0  the point groups of the space  En. In particular in the space  E2  we have point groups  G20 (rosettes), line groups  G21  (friezes) and space groups  G2, while these latter are also called plane groups, to distinguish them from their three-dimensional counterparts (space groups in the narrow sense,  G3 ).

With symmetry groups of friezes  G21  and symmetry groups of ornaments  G2 ,  a group contains one or two generating translations respectively, so that each of these groups has a translational subgroup, as we saw in Figure 11 of the previous document.

A lattice is the orbit of a point with respect to a discrete group of translations. For the (seven types of) friezes (G21) it is a linear series of equidistant points, while for ornaments (G2, i.e. the 17 plane groups P1, P2, Pm,   .  . .  etc.) we get a plane lattice.

Calling it a point lattice just means that it consists of isolated points, and when the latter form a linear series of equidistant points (i.e. arranged according to only one translation vector), such a (point) lattice we call a line lattice (linear point lattice), and when those points are regularly arranged according to two independent translation vectors, such a (point) lattice is called a plane lattice (planar point lattice), and when those points are arranged according to three independent translation vectors, the (point) lattice is called a space lattice (spatial point lattice (three-dimensional point lattice)). In patterns in which the motifs are arranged according to a linear lattice (as in friezes) the only invariant subspace is a line, while in patterns in which the motifs are arranged according to a planar lattice (as in ornaments) or three-dimensional lattice (as in real crystals), there are no invariant subspaces at all.

The five different symmetry types of plane lattices (oblique net, primitive rectangular net, centered rectangular net, square net and hexagonal net) bear the name of  two-dimensional Bravais lattices. The points of these lattices are defined by five different isohedral tesselations (tilings) which consist of parallelograms, rectangles, rhombuses, squares and regular hexagons. To the shape of the unit meshes of these Bravais lattices correspond the four two-dimensional crystal systems (where the rectangular net and the centered rectangular net imply the same shape of unit mesh). When we combine these lattices with the 10 possible planar motifs, we get the 17 plane groups (G2). The two-dimensional crystal systems and the five two-dimensional Bravais lattices are extensively treated in the last series of documents on the First Part of the website, accessible by  back to homepage.
In three dimensions we have 14 different Bravais lattices (and, depending on the shape of their unit cells, we have the six 3-D crystal systems), and when we combine these 14 lattices with the 32 possible three-dimensional motifs, we get 230 space groups (G3). When those three-dimensional motifs are chemical units, i.e. atomic configurations, then we have real three-dimensional crystals.
Because the symmetry groups of friezes  G21  are groups of isometries of the plane  E2  with an invariant line, they cannot have rotations of an order (period) greater than 2, because while a two-fold rotation (half-turn) maps this line back onto itself, the more-than-two-fold rotations rotate this invariant line to another direction making an angle (< 1800) with the original line, and so stops it from being an invariant line.
For the symmetry groups of ornaments  G2  the so-called  crystallographic restriction  holds, according to which symmetry groups of ornaments can have only rotations of the order  n = 1, 2, 3, 4, 6 .  The term  "crystallographic groups"  is used for all groups which satisfy this condition, despite the category they belong to.
In isometry groups all distances between points under the effect of symmetries remain unchanged and the congruence of homologous figures is preserved. Consequently, the same holds for all other geometric properties of such figures, so that the equiangularity (congruence of the angles of homologous figures) and the equiformity (the same shape of homologous figures) are the direct consequences of isometrism.

By considering and comparing the development of construction methods for the derivation of ornamental structures in art and geometry, one can note a few common approaches.
After considering regularities on which the simplest ornamental motifs (rosettes, friezes) are based, (based) mostly on originals existing in Nature, and after discovering the first elementary constructions, a way was opened for the creation of a wide variety of ornamental motifs and structures. This was usually achieved beginning from  local symmetry , i.e. from the one region representing a motif s.l., having included in it the motif s.str., and then arranging copies of it in a regular way, resulting in  global symmetry ,  the complete ornamental filling in of the plane in the case of periodicity. Such procedures exist in Nature, for example the multiplication of metamers ('segments', sequential parts) along the body's main axis in an arthropod animal, or -- in the non-periodic case -- the (non-periodic) arranging of antimers ('rays', counterparts) around that axis in, for example, a starfish. The mentioned procedure is a case of increasing the initial symmetry, and in the periodic case represents a series of extensions and dimensional transitions, leading directly or indirectly from the  point groups  -- the symmetry groups of rosettes  G20 ,  over the  line groups  -- the symmetry groups of friezes  G21  -- to the  plane groups  -- the symmetry groups of ornaments  G2 . In such a case, substructures (rosettes, friezes) are called generating substructures. See next Figure.

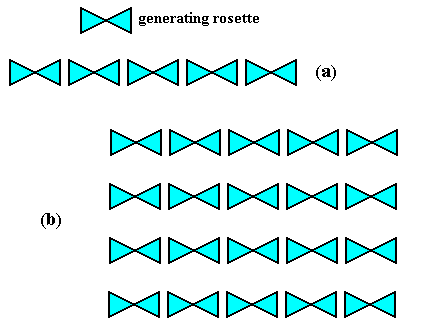
Figure 1.  Derivation (a) of frieze  pmm  (also -- as short symbol -- denoted as  mm ), and (b) of ornament (plane group)  P2mm (also -- as short symbol -- indicated as  pmm ), from generating rosette (top) with the symmetry group  D2 . (Adapted after JABLAN, 2002)
However, an almost equal role in the formation of different ornamental motifs, and especially in natural processes, belongs to the reverse desymmetrization (symmetry-breaking) procedure, a way which mainly leads from the maximal symmetry groups generated by reflections (where products of reflections result in rotations), characterized by a high degree of visual and constructional simplicity, to their subgroups. The results obtained are subgroups belonging to the same category as the original group, or (are) its subgroups with invariant subspace(s) of lower dimension(s) than that group itself has, for instance the symmetry groups of friezes  G21  as line subgroups of the symmetry groups of ornaments  G2  (In three-dimensional space we could think of the desymmetrization of a bipyramid ( Dn x D1) into a single pyramid ( Dn), by eliminating the mirror plane (equatorial plane) perpendicular to the bipyramid's main axis and intersecting that axis half-way. If we interpret these pyramids in terms of stereometric basic forms of organisms, we can say that the homopolar main body axis becomes heteropolar, expressing the fact that the organic body becomes differentiated with respect to its main axis in virtue of this symmetry-breaking).
For ornaments  G2  the maximal symmetry groups are expressed by the regular tesselations of the plane, i.e. the five two-dimensional Bravais lattices, indicated by the plane groups  P2, P2mm, C2mm, P4mm, P6mm . From these we can derive subgroups representing their desymmetrizations. These desymmetrizations can be accomplished by purely geometric means, namely by changing the symmetries of the motifs s.l. (composed motifs), or, equivalently, by the change of the shape of the fundamental region.
Antisymmetry groups

The desymmetrization can also be accomplished by means of colors. First we can use different colors just to express the above mentioned geometric changes, which means that such a use of colors belongs just to the first method of desymmetrization. But we can also use colors such that it results in so-called colored symmetry groups, from which we can easily determine subgroups as desymmetrizations. Thereby we can use several colors. When only two colors are used, for instance black and white, and if it results in a colored symmetry group, then this (colored) symmetry group is called an antisymmetry group, i.e. a colored symmetry group with only two colors. From an antisymmetry group we can easily read off the subgroup of index 2  [The index of a subgroup is : order of group / order of subgroup, where "order of a group" means the number of its elements.],  and this subgroup then is a desymmetrization (symmetry-breaking) of the given group.
We shall now exactly define what an antisymmetry group is.

Let  e1 be an antiidentity transformation which satisfies the relations

e12 = E (where E is the identity element of the given group)

e1s = se1, where  s  is any symmetry transformation of the given group.

So the antiidentity transformation  e1  is an element of period 2 and commutes with all the group elements. The transformation  s' = e1s  is then called an antisymmetry transformation. As the interpretation of the transformation  e1 ,  it is possible to accept the alternating change of any bivalent quality, geometric or not, which commutes with the symmetries of the group, for instance the color change BLACK-WHITE,  change of electricity charges  +, -,   etc. The transformation  e1  does not necessarily belong to the given group.
A group which, in addition to symmetry transformations, contains antisymmetry transformations is called an antisymmetry group.
As the basis for deriving antisymmetry groups we take some symmetry group  G  which we call a generating group of antisymmetry (or simply a generating group). By replacing some or all symmetries (generators) of the group  G  by antisymmetries (antigenerators) we obtain, as a result, an antisymmetry group  G' .  Now this resulting antisymmetry group  G'  either contains the element  e1  or not. When it contains this element, the latter is added to the generating group, resulting in

G' = G x {e1} = G x C2

Such an antisymmetry group is called a senior antisymmetry group.
When, on the other hand, the resulting antisymmetry group does not contain the transformation  e1  ( but, of course, does contain some elements of the form  se1 ), it is called a junior antisymmetry group. All junior groups are isomorphic to their generating group  G . Every junior antisymmetry group is uniquely defined by the generating group  G  and by its subgroup  H  of the index 2. Since all (normal) subgroups of the index 2 of the generating group  G  can be obtained knowing junior antisymmetry groups derived from  G ,  junior antisymmetry is included in the desymmetrization method.
When we think of the antisymmetry in terms of the color change WHITE-BLACK, where WHITE is denoted by W and and BLACK by B, we can say that we have the group of all possible permutations of the symbols (W B). This group has two elements, namely its identity element (identity permutation) W B, which means W ==> W, and B ==> B, (i.e. when it happens to be W its stays W,  when, on the other hand, it happens to be B it stays B) and (the permutation) B W, which means W == > B, and B ==> W. (i.e. when it is presently W it becomes B,  when it is presently B it becomes W).  When we now denote the latter permutation as  e1  (antiidentity transformation), and if  e1s = se1 holds for every symmetry transformation  s  of a symmetry group  G ,  then we can form an antisymmetry group  G'  from the group  G  by replacing one or more generators  g i  of the group  G  by the corresponding antigenerators  e1g i .

Let us work out a junior antisymmetry group, generated from the group  D4  which is geometrically realized as a square :

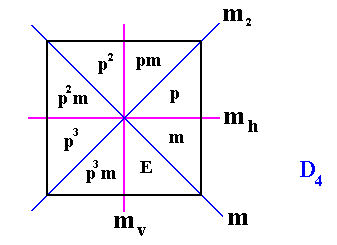
Figure 2.  Realization of the symmetry group  D4 ,  in the form of the symmetries of a Square. Its four mirror lines are indicated. Also its eight elements are indicated in terms of the generators  p  and  m .    E  is the identity element (which can be expressed as  m2 ).
The elements ( E,  p,  p2, p3 ) form the  subgroup  C4  of the symmetry group as well as of the antisymmetry group (See next Figure).
The elements  m,  pm, p2m, p3m  form the  right coset  by the element  m  with respect to the subgroup  { E,  p,  p2, p3 }  of the (generating) symmetry group.
As we can see in the above Figure, our symmetry group  D4  consists of eight elements
E,   p,   p2,  p3,  m,   pm,  p2m,  p3m ,  which can be generated by the elements  p ,  which is an anticlockwise rotation of 900 about the center of the square,  and  m ,  which is a reflection in the reflection line  m .  Further,  p4 = m2 = E  holds.
Now we're going to replace the generator  m  by the antisymmetry transformation  e1m  :

E ==> E  [because E = m2 = mm, and after substitution we get  e1me1m,  and, because  e1  commutes with every element of the group, we may write  me1e1m = mEm ( because e12 = E ) = mm = m2 = E ].
p ==> p
p2 ==> p2
p3 ==> p3
m ==> e1m
pm ==> pe1m = e1pm
p2m ==> p2e1m = e1p2m
p3m ==> p3e1m = e1p3m

Where, generally,  e1x  means a change of color of the area that represents the element  x  of the original group (the generating group of antisymmetry). We see that here the transformation  e1  itself is not an element of the resulting antisymmetry group, so the latter is a junior antisymmetry group, and is isomorphic to the generating group (i.e. the original group).
We're now going to perform those color changes in our realization of the (generating) group  D4  as it was given in Figure 2. The color change used is WHITE-BLUE (instead of white-black) :

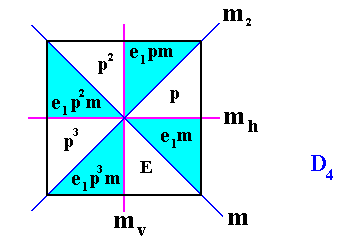
Figure 3. Junior antisymmetry group (isomorphic to  D4 ), generated by substituting the symmetry transformation  m  by the antisymmetry transformation  e1m .  Here  e1  means the color change WHITE-BLUE, of every area that represents a group element (of the resulting antisymmetry group) that contains  e1 .
The ' white ' elements ( E,  p,  p2, p3 ) form the  subgroup  C4  of the symmetry group as well as of the antisymmetry group.
If we look to the antisymmetry group of Figure 3, we can interpret its elements as follows : The junior antisymmetry group is isomorphic with the generating group, but by this antisymmetry we find subgroups, in our case the subgroup  {E,  p,  p2, p3}, which is isomorphic to the cyclic group  C4 , and this latter group has lower symmetry than the original group, so desymmetrization is indeed accomplished by using antisymmetry.
Another feature of antisymmetry groups is just as important :
While a (non-identity) symmetry transformation (generally called)  s  is just a displacement (e.g. a rotation, reflection, etc.), an antisymmetry transformation  e1s  ( =  se1 ) is a displacement  s  and at the same time involving a quality change with respect to some bivalent quality. The latter can be a change in color (within a set of two colors), for instance a change from white to black or vice versa, but it can also be some geometrical or physical quality. It is clear that antisymmetry opens up many possibilities for modelling real structures. In crystals for example we can have the case of crystalline compounds made up of two atomic species (or out of two chemical complexes for that matter), say A and B. When we go from a certain individual of atomic species A (located somewhere in a crystal) to some nearby individual of atomic species B, then we have 'performed' a displacement as well as a quality change. And this can be modelled by some antisymmetry group, provided the displacement belongs to a symmetry group, and the color change transformation as taken all by itself, i.e. the antiidentity transformation  e1 ,  commutes with every symmetry transformation of the generating group.
Antisymmetry is the simplest case of colored symmetry, namely the case where  N = 2  (where N is the number of colors used). So even more possibilities for modelling real structures are possessed by colored symmetry groups where  N  is equal to or greater than 3.  Here we could think of crystals of chemical compounds that involve three or more atomic species. And in organisms we could, for example, think of the differentiation of their metamers ('segments') into body metamers, head segments, tail segments, etc.  So let us now expound the general theory of colored symmetry for  N  is three or more.

Perhaps it is instructive to show that the antisymmetry transformations applied to some relevant antisymmetry group is indeed a 'cover-operation', which means that the image of the corresponding antisymmetry pattern is indistinguishable from the original. To illustrate this, let us consider the frieze pattern according to the line group  pmm  and derive a possible antisymmetry group by replacing the generator  t  (translation) by the antisymmetry transformation  e1t .  This new transformation means :  a translation followed by a color change between two colors, for example a change from white to black. The next Figure shows the generating group  pmm  and the resulting antisymmetry group  pmm / pmm .
In order to understand that Figure, let us derive some group elements of the antisymmetry group (where "==>" means "becomes") :

t ==> e1t .
t2 ==> (e1t)2 = e1te1t = e12 t2 = t2  (because  e12 = 1,  i.e. no color change).
t3 = tt2 ==> e1tt2 = e1t3 .

And because the antiidentity transformation  e1  is a color swap, we see that colors will alternate regularly in the resulting pattern.

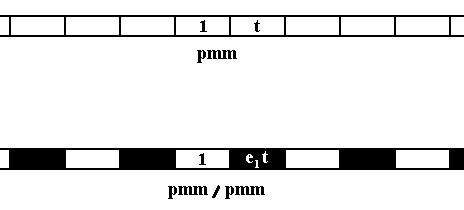
Figure 3a.  Patterns according to :  Generating symmetry group  pmm  (top image), and derived Antisymmetry group  pmm / pmm  (bottom image).  1  is the identity element, and  t  represents a translation along the frieze axis. The element  e1t  is the corresponding antisymmetry transformation.
The pattern must be imagined to be extended indefinitely to the right as well as to the left.
When we have the pattern representing the antisymmetry group  pmm / pmm  as it is depicted in the previous Figure (lower image), and when we now apply one of its antisymmetry transformations, say,  e1t ,  to that whole pattern, then what we do is in fact the following :  We shift the whole pattern to the right, according to the translation  t  and then change all the colors according to the permutation

( White Black )  (cycle notation)

which means that white becomes black and black becomes white :

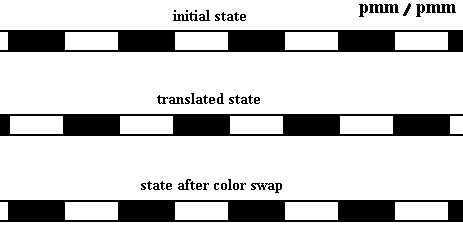
Figure 3b.  Performance of the antisymmetry transformation  e1t  on the  pmm / pmm pattern of the previous Figure (bottom image) :

The patterns must be imagined to extend indefinitely to the left as well as to the right.
As we can see in the above Figure, the final state of the pattern is indistinguishable from the initial state when applying the antisymmetry transformation  e1t  to the pattern. So it is indeed a 'cover-operation' albeit in a somewhat broader sense, and this means that an antisymmetry transformation is indeed a symmetry. It is clear that we thereby have broadened the concept of symmetry. The same is the case with colored symmetry (N equal to, or greater than 3, where N is the number of colors used).
Colored symmetry groups

Colored symmetry involves change of colors (which, as has been said, do not have to be interpreted as just colors, but as species of any polyvalent quality geometric or not). Such color changes -- all by themselves -- can be described by permutation groups.
A permutation is a one-to-one mapping of a (finite) set onto itself. So if we have a set of symbols (which can stand for anything), say {A, B, C, D}, then a permutation  x  could be for instance

A ==> B    (A becomes B), and
B ==> C    (B becomes C), and
C ==> D    (C becomes D), and
D ==> A    (D becomes A)

which (permutation) we can write as

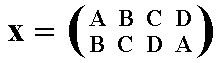
or just  (A B C D),  which is the cycle notation, in which we read off the changes from left to right, and where, arriving at the last symbol, this latter changes into the first.

Another permutation,  y,  involving this same set of symbols, could be, for instance

A ==> B    (A becomes B), and
B ==> A    (B becomes A), and
C ==> D    (C becomes D), and
D ==> C    (D becomes C)

which (permutation) we can write as

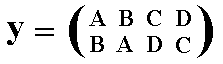
or just  (AB) (CD),  which is, again, the cycle notation, in which we see two cycles, (AB) and (CD), where each individual cycle must again be read off from left to right, and, where, arriving at the last symbol (here the second symbol), the latter changes into the first.

There are more such permutations of four symbols, in fact  4!  of them (where "4!" means "four faculty", which can be computed as 1 x 2 x 3 x 4 = 24). An important permutation among these is the identity permutation, which leaves all symbols invariant, and can be written as

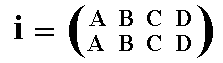
or just  (A) (B) (C) (D)  in cycle notation.

Each of these symbol changes discussed above, can stand for a color shuffling within a set of four colors.
All possible permutations of a finite set of symbols together form a group, where each group element is a permutation, and where the group operation is the successive application of two permutations (resulting again in a permutation that is an element of the group). Within such a group we can sometimes detect subgroups.
The full group of all  n!  permutations of  n  symbols is called the Symmetric Group, and is denoted  Sn ,  so that the full group of permutations of four symbols (which can stand for colors, or anything for that matter), is denoted  S4  and is of order 24.
In our exposition of the theory of colored symmetry such permutation groups will play a role.

Now, let  PN  be a subgroup of the Symmetric (permutation) Group  SN ,  i.e. let it be the subgroup of the full group of all the permutations of the color set {1, 2, 3, .  .  .  N}, where 1, 2, 3, . . . denote different colors, and let  c  be an element of  PN ,  i.e. let  c  be one of the color permutations of the group  PN ,  and let further the relation  cs = sc  hold, where  s  is any symmetry transformation of the group  G  (which is supposed to be a symmetry group -- not to be confused with the Symmetric Group  Sn  (or,  SN ) mentioned above). The latter relation means that the color permutation  c  commutes with every element of the group  G . When all these conditions are satisfied, then  s* = cs  is called a colored symmetry transformation.
A color permutation  c  can be interpreted as a change of any polyvalent quality which commutes with all the symmetries of the group  G . A colored symmetry group is a group which besides symmetry transformations contains colored symmetry transformations (colored symmetries). Also here (as in the case of antisymmetry groups) the symmetry group  G  is called a generating group of colored symmetry. The colored symmetry group  G*  derived from  G  is called a junior colored symmetry group if it is isomorphic to  G  (In the present investigation we will not consider senior colored symmetry groups).
Every junior colored symmetry group can be defined by the ordered pair (G, H) which consists of the group G and its subgroup H of the index N, i.e. [G : H] = N. Two groups of colored symmetry (G, H) and (G', H') are equal if there exists an isomorphism  i(G) = G'  which maps H onto H' (JABLAN, 2002, p. 32). For N = 2 (i.e. for two colors) and PN = C2 ,  (G, H) is an antisymmetry group.
A color permutation group PN is called regular if it does not contain any transformation (permutation), distinct from the identity permutation, which keeps invariant an element of the set {1, 2, .  .  .  N}. If it contains such a transformation, a color permutation group is called irregular.
As an example of a permutation that keeps invariant one or more elements of the set of symbols we could give :

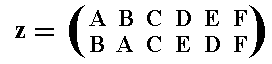
Depending upon whether the color permutation group PN is regular or not, we can distinguish two cases.
For a regular group PN every colored symmetry group is uniquely defined by the generating group G and its normal subgroup H of index N -- the symmetry subgroup of G* (but, as has just been said, also a subgroup of the group G). This results in the group/subgroup symbols of the colored symmetry groups G/H, and [G : H] = N. (JABLAN, 2002, p. 32)
For the irregular group  PN ,  in addition to G and H we must consider also the subgroup  H1  of the group G*, which maintains each individual color (or index representing it) unchanged (i.e. the group of stationariness of colors). In this case H is not a normal subgroup of G. The order of the group PN -- [Recall that the order of the group SN is always N !,  i.e. 1 x 2 x  . . . x N ] --  is  NN1 ,  where [G :H] = N,  [H : H1] = N1  and quotient group G/H1 isomorphic to PN .  To denote such colored symmetry groups, the symbol  G/H/H1  is used (JABLAN, 2002, p. 32).

Also in this case, i.e. in the case of colored symmetry groups involving more than two colors (which we simply call colored symmetry groups, as such distinguishing them from antisymmetry groups -- which involve only two colors), we have to do with displacements (translations, rotations, reflections, etc.) accompanied by a quality change, but now a change of some polyvalent quality. So indeed colored symmetry groups can model a wide variety of real structures.

We're now going to explain the above, by considering some concrete cases of colored symmetry groups.
We start with the case (first example) where the color permutation group PN is regular, and the symmetry group  G  is the cyclic group C4.

Figure 4. Realization of the cyclic symmetry group  G  with structure  C4 .
It consists of four elements :

p4 = E .
We now associate a color permutation group P4 with this symmetry group  G .  This color permutation group -- which itself is a subgroup of S4, the group of all permutations of a set of four symbols -- consists of four permutations of a set of four colors {1, 2, 3, 4} (colors here given by indexes) :

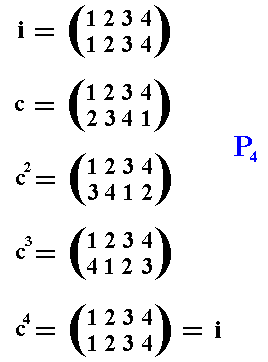
We can see that in this color permutation group there is no non-identity permutation that leaves one or more elements of the set {1, 2, 3, 4} unchanged, so this color permutation group  P4  is regular.

From the elements of this permutation group we choose the element  c ,  i.e. the color permutation

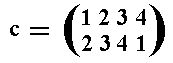
which in cycle notation is  (1234), implying that the period of  c  is 4, which means that  c4 = i ,  where  i  is the identity permutation.

Now we're going to replace the generator  p  by the color generator  cp ,  which means that  p  becomes  cp ,   p2  becomes  cpcp ,  which, because  c  commutes with every element of G, is equal to  c2p2 ,  and in the same way  p3  becomes  c3p3 .  The identity element E of group G can be written as  p4 ,  and applying the replacement to it will result in the following sequence of derivation :  E = p4 ,  which becomes  cpcpcpcp ,  and, again, because  c  commutes with every element of group G, we can write  c4p4 ,  which is equal to  c4E = iE , where  i  is the identity permutation, implying that our final result of applying the replacement to E is  E .  When all this is done we have created the colored symmetry group  G*  from the generating group of colored symmetry  G .  Both groups are isomorphic to  C4 .
To show that we have indeed created a colored symmetry group we must see that the transformation  c  commutes with every symmetry transformation of the (generating) group G.  And this is easily seen :  Whether we first perform the symmetry transformation on some group element and then provide it with the altered existing color of that element according to the permutation  c ,  or when we first perform the color change of the existing color of the element and then perform the symmetry transformation on that element, resulting in the new element having this new color, makes no difference. The same applies to the color changes according to  c2  and  c3 .
Let us see our concrete example. We will let the above permutations  c, c2  and  c3  be color permutations involving four colors indicated by the numbers 1, 2, 3, 4. See next Figure.

Figure 5.  Color change of the areas representing group elements of the group depicted in Figure 4 according to the permutations  c, c2  and  c3.
We will now expose exactly what happened to the generating group G (having the structure of C4 ). Thereby we must first note the following :
c  is the permutation (1234) (cycle notation). It changes the initial color 1 (the color of the identity element) to the color 2.
c2  is two times applying  c.  It thus changes the initial color 1 to the color 3.
c3  is three times applying  c.  It thus changes the initial color 1 to the color 4.

Starting with the identity element (whose color -- yellow -- remains unchanged), we rotate 900 anticlockwise about the center of the square and change color 1 (yellow) (as it is present in the area representing the identity element) to color 2 (red). So in all we have performed the color symmetry transformation  cp ,  and it is clear that this has the same effect, as when we had performed  pc ,  i.e. if we first changed color 1 to color 2, and then rotate 900 anticlockwise about the center of the square.

We rotate 1800, which is equivalent to two times performing  p  (to the identity element), and change color according to two times applying color permutation  c  to color 1, resulting in color 3 (1 ==> 2,  2 ==> 3). So we have performed the color symmetry transformation  c2p2 ,  which is equal to  p2c2.

We rotate 2700 anticlockwise, which is equivalent to applying  p  three times (to the identity element) and change color 1 according to three times applying the color permutation  c , resulting in the color 4 (1 ==> 2,  2 ==> 3,  3 ==> 4). So we have performed the color symmetry transformation  c3p3 ,  which is equal to  p3c3 .

We rotate 3600 anticlockwise, which is equivalent to applying  p  four times (to the identity element) and change color 1 according to four times applying the color permutation  c , resulting in the color 1 (1 ==> 2,  2 ==> 3,  3 ==> 4,  4 ==> 1). So we have performed the color symmetry transformation  c4p4 ,  which is equal to  p4c4 . And because  p4 = E  and  c4 = i  (where  i  the identity permutation), we have in effect not done anything to the initial element, i.e. we have got an element that we already had, namely the identity element.

So our colored symmetry group G*, derived from the group G, has the following group elements :  E,  cp,  c2p2,  c3p3.  These were obtained by replacing the symmetry generator  p  by the colored symmetry generator  cp .
To show that the resulted color symmetry group G* is isomorphic to the generating group G, which has the structure of C4 ,  we must determine the periods of its elements :

E  has of course period 1.

The element  cp .
(cp)4  = cpcpcpcp = c(pc)(pc)(pc)p, and because  c  commutes with every element of the generating group G, we can write  ccpcpcpp , which is equal to  cc(pc)(pc)pp, which is  cccpcppp, which is  ccc(pc)ppp, which is ccccpppp, which is  c4p4, which is  c4E, which is  c4, and, because  c4 is the identity permutation, our final result is  (cp)4 = E, which means that the period of the element  cp  is 4.

The element  c2p2 .
(c2p2)2  = c2p2c2p2 = c2c2p2p2 = c4p4 = E, so the period of the element  c2p2 is 2.

The element  c3p3 .
(c3p3)4  = c3p3c3p3c3p3c3p3 = c3(p3c3)(p3c3)(p3c3)p3 = c3(c3p3)(c3p3)(c3p3)p3 = c3c3p3c3p3c3p3p3 = c3c3(p3c3)(p3c3)p3p3 = c3c3(c3p3)(c3p3)p3p3 = c3c3c3p3c3p3p3p3 = c3c3c3(p3c3)p3p3p3 = c3c3c3(c3p3)p3p3p3 = c3c3c3c3p3p3p3p3 = c12p12 = (c4)3(p4)3 =
( i )3E3 = E (because  i  is the identity permutation). So our result is  (c3p3)4 = E, which implies that the period of the element  c3p3  is 4.

So our colored symmetry group G* contains one element of period 1 (identity element), one element of period 2, and two elements of period 4, and this is the finger print of a group with structure C4 .

The upshot of all the forgoing is the following :
If we look to the image of Figure 5 we see a structure that, if we take the colors into account, has no symmetry whatsoever, although it looks in some way more or less ordered (it reminds us of four-fold structure). Within the theory of symmetry groups we can do nothing with the observed quasi four-fold structure. And, of course, we should wish to account for that structure in order to distinguish it from any hopelessly irregular structure such as :

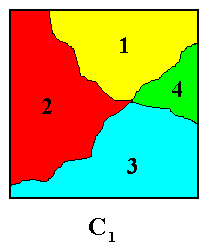
Figure 6.  Irregular structure with no symmetry at all, implying it to have the structure of  C1 .
And indeed the theory of colored symmetry comes to the rescue, because we find out that the structure depicted in Figure 5 can be derived from the group G (as depicted in Figure 4 and which has the structure of C4 ),  by replacing the generator  p  (of group G) by the color generator  cp  where  c  is a color permutation that, as a transformation, commutes with every element of the group G.
And because the resulting color symmetry group G* (being a junior color symmetry group) is isomorphic with the generating group G (as junior groups should be), it has the structure of C4 (instead of only that of C1 ). So with the aid of the theory of color symmetry we indeed have been able to account for the four-fold aspect of the structure depicted in Figure 5.

This color symmetry group with the structure of C4 ,  can be denoted by the symbol  C4 / C1 ,  where C4 refers to the generating group (generally G), while C1 refers to the subgroup  {E}  (generally H).

When we look to the group G, as depicted in Figure 4, we have the full C4 symmetry. The subgroup {E}, consisting of the identity element only, is a normal subgroup of G, because its left coset with respect to any element of the group is equal to its right coset (as such satisfying the definition of subgroup to be normal). The equality of those cosets follows from the relation  sE = Es  for every element of the group. So the element  p  is pE = Ep, and as such is a coset of the subgroup {E}. Also the element  p2 is p2E = Ep2, and as such is a coset of the subgroup {E}. In the same way  p3  is a coset of the subgroup {E}.
When we now look to case where colors are brought in, as in Figure 5, we see the normal subgroup {E} represented by color 1 (yellow), and its cosets represented by the colors 2, 3 and 4.  And as such this normal subgroup {E} represents -- together with its cosets -- a desymmetrization (symmetry-breaking) of the group G, having C4 structure, to the group G*, having C1 structure as long as we interpret this group as just a symmetry group (where the colors effect asymmetries) and not as a colored symmetry group. As has been said, this desymmetrization can be denoted by C4 / C1 .

Now we have the symmetry group  G = {E,  p,  p2,  p3}  with the structure  C4 ,  and we have the corresponding  c o l o r e d  symmetry group  G* = {E,  cp,  c2p2,  c3p3} ,  also with the structure  C4 .
What is the difference between these two groups? Well, although their algebraic structure is identical, they differ in their respective element content :  While the non-identity elements of G are just symmetry transformations, i.e. displacements, the (non-identity) elements of G* are color transformations (displacements followed by a color change).
Both groups, G and G*, thus are two different realizations of the abstract group  C4 ,  and this abstract group can be defined by the following (abstract) group table :

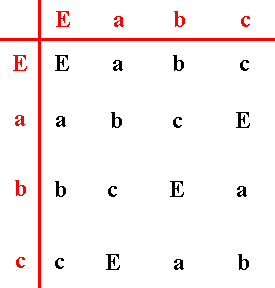
In this table the C4 structure is completely defined without any interpretation of the letters  E, a, b, c.  Only how they combine is given by the table, and that is enough to pin down the structure.
When we now interpret the letters  a, b, c  as the rotations  p,  p2,  p3 ,  where  p  is an anticlockwise rotation of 900, we get the group  G .
When, on the other hand, we interpret the letters  a, b, c  as the colored symmetry transformations  cp,  c2p2,  c3p3 ,  where  c  is the color permutation  (1234) ,  and  p  is again an anticlockwise rotation of 900 ,  we get the colored symmetry group  G* .  Thereby we know that we can interpret the color permutations as changes of any polyvalent quality, geometric or not. In crystals (while going over to three dimensions) we could think of 'going' from one individual atomic complex of species A to an individual of an atomic complex of species B in the same crystal lattice, i.e. we then talk about the transformation of one element into another in a permutation of a set of atomic complexes, for example going from an SiO4 complex to an OH complex.

We can thus describe many real structures by means of an extended symmetry theory.
Thereby we could ask ourselves what the reality status is of the groups that have been used for such a description. Is that status solely that of a description or is it more than that? If we think about such a group, like for instance the group C4 ,  as a description of the symmetry of an object, then we have, on the one hand, that symmetry present in the object, and, on the other, the mathematical description of it. But what then is that symmetry that has been described? When taken all by itself it cannot be a material entity, a thing, because it cannot materially exist as such. We could say that it is one of the properties of the structure of the given object. But that is too general and doesn't answer our question. What, in the present case, is the difference between the grouptheoretical description of the symmetry present in the object and that symmetry itself? The answer, in my opinion, is that there is no difference at all between the two, as soon as we do not consider the contingent and subjective aspects of that description, for example the fact that the description is thought (by a brain) or is written down on some medium, further, the use of certain conventional mathematical symbols, etc. Said in other words, if we eliminate from the grouptheoretic description all the contingent elements, we are left with the symmetry itself. The upshot is that the group (with specified group elements) IS the symmetry. Thus, with the group, we have found the immaterial structural aspect, representing (in the sense of actually being) the symmetry, of the given object (and have found that aspect) in all its details and ramifications. This immaterial aspect is realized in the given material object, in the sense of matter participating that immaterial 'idea'. This reception by (prime) matter of that immaterial idea must not be understood causally, but as a fact of metaphysical constitution of that given object. Causally the symmetry -- as symmetry of that object, and only when this symmetry is intrinsic to this object, i.e. not imposed from outside the object -- originates as the result of the workings of a certain dynamical system, thereby, in many cases, involving instabilities, effecting a shoving off to a certain definite and stable solution.
So the reality status of the group is not solely that of a description, but also that of an 'object' existing in some immaterial domain. So subjectively that group exists in the minds of mathematicians and other scientists, but objectively it exists in the just mentioned immaterial domain, waiting as it were, to be participated by prime matter, which then becomes the carrier of that group, and thus of that particular symmetry.
As a second example of colored symmetry, we consider the case where the color permutation group PN is (also) regular (i.e. not containing any permutation which keeps invariant one or more elements of the set of symbols {1, 2, 3, .  .  .  N}, except for the identity permutation.), and that as such will be taken for the case where the generating group G is the group  pmg ,  which can be realized as one of the seven frieze patterns. (A frieze pattern is a pattern of motifs, repeating regularly along a line. They will be discussed further down).
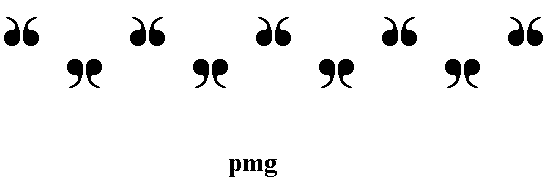
The line group  pmg  can be realized as (or represented by) the following frieze pattern :

Figure 7.  A possible realization of the group  pmg .
The pattern must be imagined to extend indefinitely to the right as well as to the left.

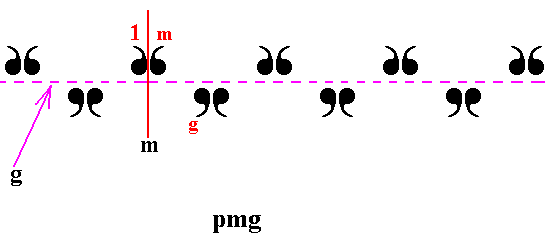
Figure 8.  The group  pmg  can be generated by a glide reflection  g  parallel to the frieze axis and a reflection  m  in a reflection line perpendicular to the frieze axis.

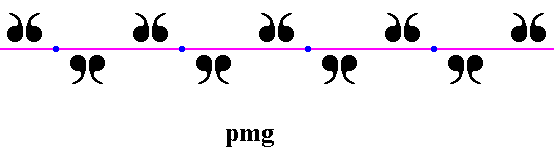
Figure 9.  The repetition of motifs is described by a one-dimensional point lattice (indicated by blue dots and connection lines). Each lattice node (lattice point) is associated with an equivalent area of the pattern (i.e. the surroundings of each node are identical). As such each lattice node is associated with four units (commas) of a motif s.str. ,  itself consisting of four motif units, commas). Each such motif unit (comma) can represent a group element.
On the basis of the point lattice determined above, we can depict the  motifs s.l.  of our  pmg  pattern. See next Figure.

Figure 10.  Motifs s.l.  (blue and red strips) of the  pmg  pattern under consideration. Each motif s.l.  is associated with a lattice node and consists of one motif s.str.  (itself consisting of four asymmetric units (commas)) PLUS corresponding back ground. Each motif s.l.  extends indefinitely upwards and downwards. The red and blue colors do not signify any asymmetry, but only serve to highlight the motifs s.l.  The dark blue dots represent lattice points. The figure illustrates the fact that the frieze is carried by the two-dimensional plane (E2).
When we now partition these motifs s.l.  properly, we obtain maximal areas (the fundamental region and its copies) that represent group elements :

Figure 11.  Partition of the motifs s.l.  such that the resulting areas (red, blue) represent group elements. Each such area contains one (asymmetric) unit (comma) of the motif s.str.  and extends indefinitely upwards and downwards.  The dark blue dots represent lattice points. The colors red and blue do not -- in the present context -- signify any asymmetry, but only serve to highlight the group elements.
The next Figure adds some markings to some areas in order to point to the identity element  1  and the generators  g  (glide reflection parallel to the frieze axis) and  m  (mirror reflection in the line  m  perpendicular to the frieze axis).

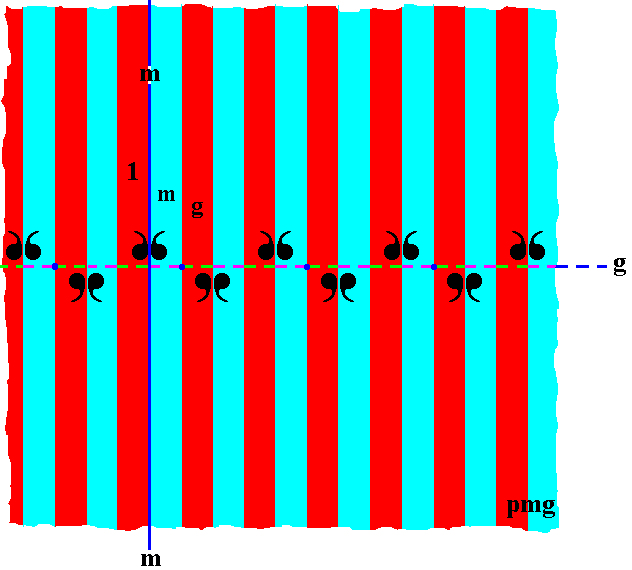
Figure 12.  Indication of the identity element, and of the two (possible) generators of the group  pmg . The mirror line  m  (solid vertical line) and the glide line  g  (dashed horizontal line) are indicated.
In the next Figure the rest of the areas (of the displayed part of the pattern) have been filled in with the proper symbols of the group elements (or we can say, we have generated the group from the initial element -- identity element -- by repeatedly applying the two generators  g  and  m ).

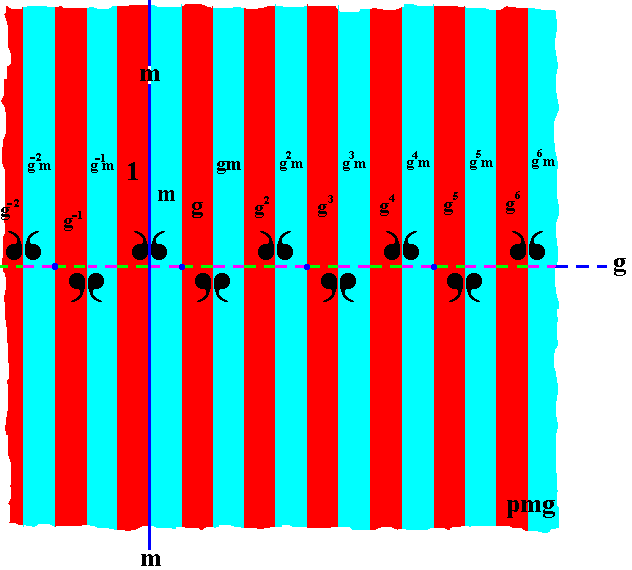
Figure 13.  Generation of the group  pmg .
Each vertical area of the displayed part of the pattern is provided with a mark that tells what group element is being represented by that area. The colors red and blue of the areas do not -- in the present case -- signify any asymmetry, they only serve to highlight the group elements.
In the above Figures the symmetries and asymmetries were indicated by the positions, mutual relations and orientations of the units (commas) of the motifs s.str. The colors of the areas were not supposed to express these symmetries, but only to highlight the fundamental region and its copies.
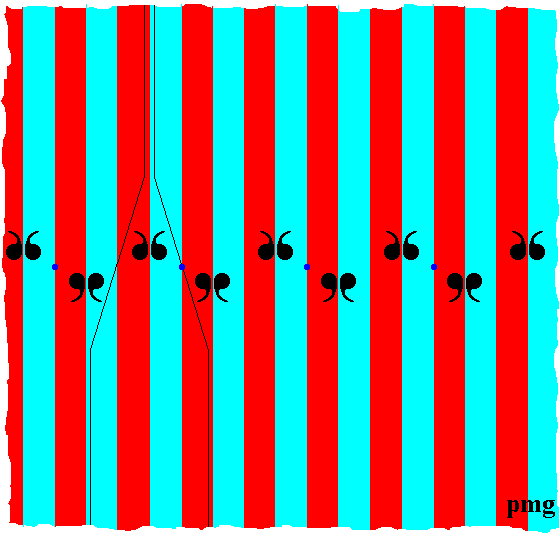
But now we are going to consider colored symmetry, where colors should express the structural features of the pattern. So we must dispose of the units (commas) of the motifs s.str.  and replace what they express,  by the shape of a newly chosen fundamental area and its copies, i.e. the shape, position and orientation of the newly chosen fundamental area and its copies (also representing group elements) should express all the symmetries present in the  pmg  pattern. And when we then bring in different coloring of those areas we will create a colored symmetry group which -- as a junior group -- is isomorphic to the generating group  pmg . See next Figures.

Figure 14.  First phase of construction of new fundamental areas accounting for all symmetries of the  pmg  pattern. The colors still do not signify symmetries or asymmetries of the pattern.

Figure 15.  Construction of the new fundamental region and its copies (red, blue). As before, each such region (area) contains one unit (comma) of the motif s.str. ,  and the colors still do not signify symmetry features, but only highlight the new fundamental region and its copies. We can clearly see that the shape, position and mutual relation of these new areas (representing group elements) express the glide reflections, mirror reflections and the (implied) 2-fold rotation axes. Each area extends indefinitely upwards as well as downwards, and the pattern extends indefinitely to the right as well as to the left. The lattice nodes are indicated by dark blue dots.
Because the function of the units (commas) of the motifs s.str.  has been taken over by the shape, position and mutual relation of the fundamental region and its copies, we can erase the commas :

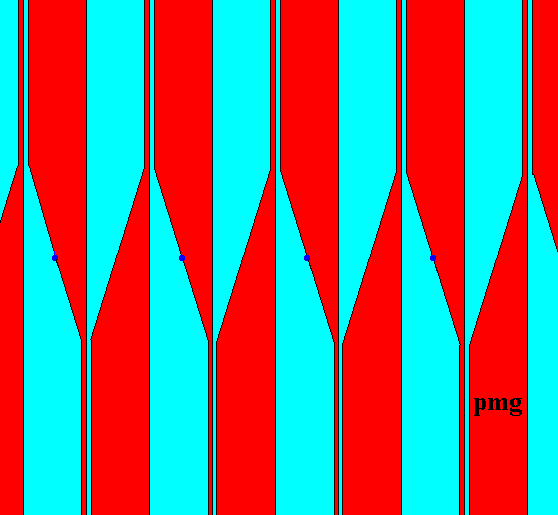
Figure 16.  Erasion of the commas. The pattern of fundamental regions now expresses all the symmetries of the group  pmg .  The dark blue dots represent lattice nodes.
The next Figure shows the group elements explicitly in the commaless pattern.

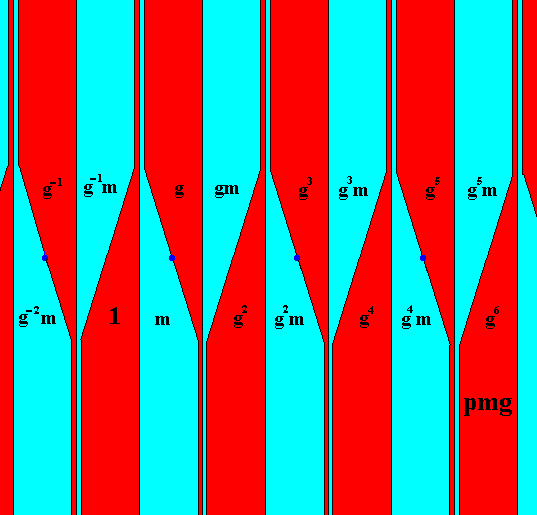
Figure 17.  Identification of the group elements, each represented by a fundamental area or one of its copies (red, blue). The colors red and blue still do not signify symmetry features of the  pmg  pattern.
Because now the shape, position and mutual relations of the areas represent the symmetry features of the  pmg  pattern we can erase the colors, i.e. we can use one and the same color for all the areas :

Figure 18.  The  pmg  pattern as plane tesselation by the orbit of the fundamental region, as established in the previous Figures. Each such area has the same color (yellow). The blue dots indicate the lattice nodes. Identities of the group elements are indicated.
The group  G = pmg ,  as depicted in the above Figure can now be seen as the  generating group of colored symmetry,  i.e. from this group we can derive several differnt color symmetry groups that are all isomorphic to this generating group. The example we choose, namely  pmg / p11 ,  will involve the regular permutation group of four colors,  P4 , and, taken from it, the system of colored generators  {c1g, c2m},  or, equivalently,  {c2m, c1c2h} ,  where  g  is a glide reflection parallel to the frieze axis,  m  a mirror reflection in a line perpendicular to the frieze axis,  h  a half-turn, and where  c1  is the color permutation

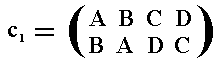
or, in cycle notation  (AB) (CD)

while  c2  is the permutation

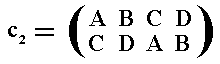
or, in cycle notation  (AC) (BD)

As can be seen, no elements remain invariant, by these permutations.
We can compute the permutation  c1c2  (first  c2 ,  then  c1 ), which is equal to  c2c1  (first  c1 ,  then  c2 ) :

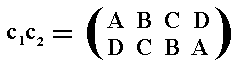
or, in cycle notation  (AD) (BC)

Also here no elements remain invariant.
The symbols  A, B, C, and D  will stand for different colors.
In addition to the identity color permutation (no colors at all changed) we have three elements,  c1, c2 and  c1c2  of period  2 ,  so these four color permutations form a group  P4  with structure D2 . And because no non-identity permutation of this group leaves an element unchanged, it is a regular permutation group.

We will now generate our colored symmetry group G* from the generating symmetry group G = pmg  by means of the generators  c1g  and  c2m ,  where  c1  and  c2  belong to the just mentioned regular permutation group  P4  (which is a subgroup of  S4 , i.e. the group of all permutations of four symbols (or colors)).

Our initial color, as being the color of all elements of the group  pmg ,  and being (and staying) the color of the identity element of that group, we denote as the color  A  (as it occurs in the permutations above). This initial color A will be changed by colored symmetry transformations, i.e. symmetry transformations of the given symmetry group (in our case the group  pmg) that are combined with a color permutation of the permutation group  P4 ,  which, in addition to the identity permutation, consists of the permutations  c1, c2  and  c1c2 ,  all of period 2.
We know that  c1c2 = c2c1 ,  and that  c12 = 1  (identity permutation),  c22 = 1 ,  and  (c1c2)2 = 1 ,  and we know further that the color permutations  c1, c2  and  c1c2  commute with all elements of the (generating) group  G ,  i.e. each color permutation commutes with all symmetry transformations of the group G.
We also know that the permutation  c1  means :
If the color is presently A, it becomes B.
If the color is presently B, it becomes A.
If the color is presently C, it becomes D.
If the color is presently D, it becomes C.
In the same way we must read the other two color permutations.

Let us now generate the elements of the colored symmetry group  G* (which is isomorphic to  pmg ).

By reflecting the identity element  1  (which has color A) of group G = pmg  in the reflection line  m  (see next Figure), we get the element  c2m ,  the first generator. Its meaning is :
First reflecting in the line  m  and then change color A into color C, according to the permutation  c2 ,  or vice versa.
By subjecting the identity element of group G = pmg  to a glide reflection along the glide line  g ,  we get the element  c1g ,  the second generator. Its meaning is :
First the glide reflection  g  and then change color A into color B, according to the permutation  c1 .
Combining these elements we get :

(c1g)2 = c1gc1g = gc1c1g = gc12g = gg = g2 .
(c1g)3 = c12c1g3 = c1g3 .
(c1g)4 = (c1g)2(c1g)2 = g2g2 = g4 .
(c1g)5 = (c1g)4c1g = g4c1g = c1g5 .
(c1g)6 = (c1g)4(c1g)2 = g4g2 = g6 .
c1gc2m = c1c2gm .
(c1g)2c2m = g2c2m = c2g2m .
(c1g)3c2m = c1g3c2m = c1c2g3m .
(c1g)4c2m = g4c2m = c2g4m .
(c1g)5c2m = c1g5c2m = c1c2g5m .

Because  g  must be replaced by  c1g  (and  m  by  c2m ),  g-1  must be replaced by  (c1g)-1 = g-1c1-1 = c1-1g-1 .  And because the element  c1 is of period 2, we have
c1c1 = 1 = c1c1-1 ,  thus  c1-1 = c1 .  So  g-1  must be replaced by  c1g-1 .

g-1m  must be replaced by  c1-1g-1c2m = c1-1c2g-1m = c1c2g-1m .
So  g-1m  must be replaced by  c1c2g-1m .

g-2 = g-1g-1 ,  and this must be replaced by  c1-1g-1c1-1g-1 = c1-2g-2 .
c1-2 = c1-1c1-1 = c1c1 = c12 .
It then follows that  c1-2g-2 = c12g-2 = g-2  (because c12 = 1),  so that
g-2  must be replaced by  g-2 .

g-2m = g-1g-1m ,  and this must be replaced by  c1-1g-1c1-1g-1c2m = c1-2c2g-2m =
c12c2g-2m = c2g-2m ,  so that
g-2m  must be replaced by  c2g-2m .

And because the generator  c1g  implies the element  c1g-1 ,  we have this very element, but then also :
c1g-1c1g-1 = c12g-1g-1 = g-2 .
c1g-1c2m = c1c2g-1m .
c1g-1c1g-1c2m = c2g-2m .

With respect to the identity element  1  we can say the following :
1 = mm = m2 . For the color symmetry group to be generated the generator  m  must be replaced by  c2m ,  implying that the identity element  1  becomes  c2mc2m ,  which is equal to  c22m2 = m2 = 1.  So the element  1  stays  1 .

On the basis of all these calculations we can fill in the pattern of areas representing group elements and marked as being elements of the generating group G, as we had them established in Figure 18, with the corresponding permutations that, combined with the existing symmetry transformations, form colored symmetry transformations, like
c1g,  (c1g)2 ( =  g2 ),  c1gc2m ( =  c1c2gm ),  etc.
The result is given in the next Figure. For clarity reasons we have placed the symbols indicating color permutations more or less apart from the symmetry transformations. We should however read them together, like for instance  c1c2 and  g3m ,  that must be read as  c1c2g3m .

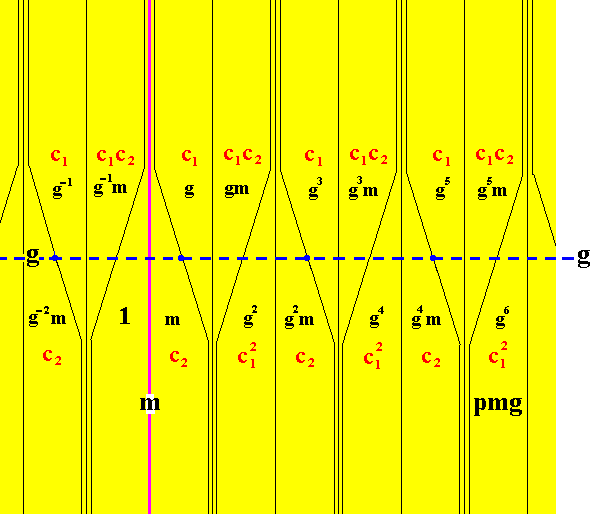
Figure 19.  Color symmetry group (colors not yet filled in)  G* ,  generated from the group  G  ( The group  pmg ), by means of the colored generators  c1g  and  c2m ,  where  c1  is the permutation  (AB) CD) ,  c2  is the permutation  (AC) (BD)  and  c1c2  is the permutation  (AD) (BC) ,  and where further  g  is a glide reflection along the frieze axis, and  m  a reflection in a mirror line  m ,  perpendicular to the frieze axis.
In the next Figure we're going to fill in the colors corresponding to the symbols  A, B, C, D,  according to the permutations of these symbols as just established.
For example, when the present color is A, and we have to do with the color transformation  c1c2gm ,  then we first perform  m ,  then  g ,  and then change color A according to the permutation  (AD) (BC) ,  which means for the present color A :

A ==> D

Recall that
c12 = 1 (identity permutation).
c22 = 1 (identity permutation).
(c1c2)2 = 1 (identity permutation).
c1c2 = c2c1 .
The permutations  c1,  c2  and  c1c2  commute with every element of the generating group  G = pmg ,  and form the regular permutation group  P4 ,  which is a subgroup of the group  S4 ,  the group of all permutations of four symbols (colors).

In terms of color change of the color (A) of the identity element the permutation

c1 means :  A ==> B .
c2 means :  A ==> C .
c1c2 means :  A ==> D .

Figure 20.  Colored symmetry group  G* ,  derived from the group  G = pmg ,  with colors added according to the permutations figuring in the color transformations.
The next Figure is the same as the previous one, but with the markings omitted.

Figure 21.  Colored symmetry group  G* ,  derived from the group  G = pmg .  Markings omitted.
If we inspect the above Figure, we see, that if we interpret the colors as structural features, but WITHOUT involving the theory of colored symmetry groups, we have a frieze pattern that has only translational symmetry, which implies that the frieze, so considered, is a representation of the group  p11 ,  and this is the lowest symmetry that can occur in friezes. Indeed we see that the following asymmetric unit was (in the above Figure) being repeated according to a translation :

Figure 21a.  Asymmetric pattern-unit that, when repeated according to a horizontal translation, yields the pattern of Figure 21.
This unit, although asymmetric, has -- as can be seen -- a certain definite structure. But this structure is not accounted for by the group  p11 .
If, on the other hand, we involve the theory of colored symmetry groups with respect to the pattern of Figure 21, then we have the colored symmetry group  G* ,  which is isomorphic to  pmg . So it is clear that  EXTRA STRUCTURE  (as was evident in the repeated units) is revealed (i.e. accounted for) that was concealed in a seemingly low symmetric pattern. Thus, what could not be accounted for by the theory of symmetry groups, could be accounted for by the theory of colored symmetry groups. Thereby it is interesting to note that the structure (i.e. the algebraic structure) of the group  p11  is  Cinfinite  (which means that it is isomorphic to the abstract group  Cinfinite ),  while the group  pmg  has  Dinfinite  structure.

The set of yellow elements of the group  G*  (one of which is the identity element) is the subgroup p11 ,  revealed by the desymmetrization of the pattern as we had it in Figure 18, and which resulted in the pattern as depicted in Figure 21. Because of this subgroup, the colored symmetry group is denoted by  pmg / p11,  or in short form,  mg / 11 . The just mentioned subgroup  p11  is normal in  pmg ,  as is the case whenever the permutation group  PN  is regular (i.e. no permutations in which one or more elements of the set {1, 2, .  .  .  N} remain unchanged) (JABLAN, 2002, p. 41). The elements of this subgroup, let us call it  H ,  are (See Figure 20) :

.  .  .  g-2,  1,  g2,  g4,  g6  .  .  . 

(yellow elements of Figure 20)

And because here the associated color permutations are all equal to  c12 ,  which in turn is equal to the identity permutation, this subgroup H is a subgroup of the symmetry group G as well as of the colored symmetry group G*. Here we shall concentrate on H as a subgroup of G.

The blue elements of Figure 20 form the right coset of the just mentioned subgroup  H  of G  by the element  m .
This coset  Hm  is equal to {.  .  .  g-2,  1,  g2,  g4,  g6  .  .  . }m  =
{.  .  .  g-2m,  m,  g2m,  g4m,  g6m  .  .  . },
and despite the fact that  g  and  m  do not commute, this right coset is equal to the corresponding left coset  mH  :
mH = m{ .  .  .  g-2,  1,  g2,  g4,  g6  .  .  . } =
{ .  .  .  mg-2,  m,  mg2,  mg4,  mg6  .  .  . }.
We can see, for instance, (See Figure 20) that although  mg2  is not equal to  g2m ,  it is equal to  g-2m  which is indeed an element of Hm.  This is the case with all the elements of Hm, so that mH = Hm.  And this -- as can be proved -- is not only the case with the element  m ,  but with all elements of G = pmg , which means that the subgroup H is normal in G.

The green elements of Figure 20 form the right and left coset of our subgroup H (yellow elements), by the element  g-1m  :
g-1mH = Hg-1m =
{ .  .  .  g-2,  1,  g2,  g4,  g6  .  .  . }g-1m =
{ .  .  .  g-2g-1m,  g-1m,  g2g-1m,  g4g-1m,  g6g-1m  .  .  . } =
{ .  .  .  g-3m,  g-1m,  gm,  g3m,  g5m  .  .  . }.

The red elements of Figure 20 form the right and left coset of our subgroup H (yellow elements), by the element  g-1  :
g-1H = Hg-1 =
{ .  .  .  g-2,  1,  g2,  g4,  g6  .  .  . }g-1 =
{ .  .  .  g-2g-1,  g-1,  g2g-1,  g4g-1,  g6g-1  .  .  . } =
{ .  .  .  g-3,  g-1,  g,  g3,  g5  .  .  . }.

So we see (Figure 20) that the subgroup H, together with its cosets, form the desymmetrization of the group  pmg , i.e. by the corresponding colorations of the subgroup H (yellow) and its cosets (blue, green, red), the symmetries of the group  pmg  are broken, except for the translation, resulting in the group  p11 .  The repeated unit in this group is : {yellow, blue, red, green} (Figure 21a), i.e. these four patches together form a motif that is being repeated according to a translation. And if we now consider these colors in the context of the theory of colored symmetry groups, then we see that this group, which we just established as being  p11  (and thus having Cinfinite structure),  is a colored symmetry group isomorphic to the group  pmg ,  which has Dinfinite structure.
The next two examples of colored symmetry groups are concerned with the case where the associated color permutation group  PN  is irregular, which means that this group contains at least one permutation (as one of its group elements) in which one or more elements of the set of symbols (colors) remains invariant under the permutation.

The first example concerns the generating group  D4 , as realized in the next Figure.

Figure 22.  Realization of the dihedral symmetry group  D4 .  Its group elements are expressed in terms of the two generators  m1 ,  which is a mirror reflection in the line  m1 ,  and  m2 ,  which is a mirror reflection in the line  m2 .
1  is the identity element (which can be expressed as  m12 ).
In order to identify the present group explicitly, we must determine the periods of its elements.
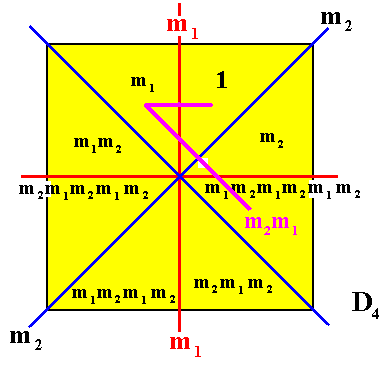
The identity element is, of course, always of period 1.
To determine the remaining periods it is important to know that the two generators  m1  and  m2  do not commute (See next Figures) :

Figure 23.  When, starting from the identity element, we first perform the transformation  m1 ,  and then, on the result, the transformation  m2 ,  (having thus performed the transformation  m2m1 ), we end up at the 4 o'clock octant of the square (as indicated), and see that  m2m1  is equivalent to  m1m2m1m2m1m2  [ = (m1m2)3 ] .
(m2m1  is a clockwise rotation of 900, while  (m1m2)3 is three times that rotation the other way around, amounting to the same rotation.)  [See next Figure].

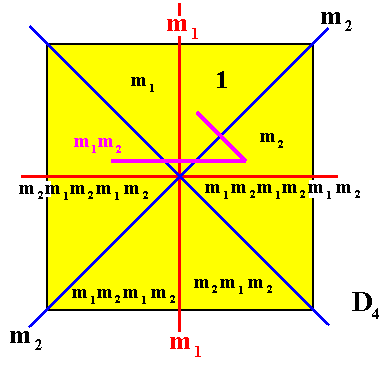
Figure 24.  When, starting from the identity element, we first perform the transformation  m2 ,  and then, on the result, the transformation  m1 ,  (having thus performed the transformation  m1m2 ), we end up at the 10 o'clock octant of the square (as indicated), which shows that  m2m1  is not equivalent to  m1m2 ,  i.e. the elements  m1  and  m2  do not commute.
In the mean time we have seen that the transformation  m2m1  is equivalent to an anticlockwise rotation of 2700 about the center of the square, and that the transformation  m1m2  is equivalent to an anticlockwise rotation of 900 about the center of the square.
Let's now determine the periods of the elements of the present group. So in total we have :

One element of period 1 (identity)
Two elements of period 4
Five elements of period 2

And this is indeed the fingerprint of a group with structure D4.

Now we're going to replace the symmetry generators  m1  and  m2  by the color symmetry generators  c1m1  and   c2m2  respectively. The color permutations  c1  and  c2  are respectively :

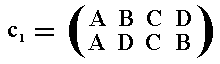
or, in cycle notation  (BD)

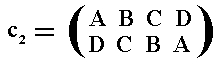
or, in cycle notation  (AD) (BC)

We see that in the permutation  c1  some elements of the set {A, B, C, D} remain unchanged, so the permutation group  P4  to which this permutation belongs, is irregular.
Further we see that both permutations  c1  and  c2  are of period 2 ,  which implies that  c12 = 1 (identity permutation),  and  c22 = 1 (identity permutation).

The identity element  1  of the generating group can be written as  m12 ,  so the above mentioned replacements result in :  1 = m1m1  ==> c1m1c1m1 = c1c1m12 = c121 = 1 (because c12 is the identity permutation). So 1 will remain 1.

The next table of group elements shows the elements that emerge when the symmetry generators are replaced by color symmetry generators, as specified above. In the first column we have placed the group elements of the generating group  G = D4  (See Figure 22).  In the second column we show the replacements. The third column, finally, shows a reshuffling of the constituent transformations, allowable because the color permutations  c1  and  c2  commute with every element of the generating group G.  As such we then get the elements of the colored symmetry group G* .

G replacement G*
1 1 1
m1 c1m1 c1m1
m1m2 c1m1c2m2 c1c2m1m2
m2m1m2m1m2 c2m2c1m1c2m2c1m1c2m2 c2c1c2c1c2m2m1m2m1m2
m1m2m1m2 c1m1c2m2c1m1c2m2 c1c2c1c2m1m2m1m2
m2m1m2 c2m2c1m1c2m2 c2c1c2m2m1m2
m1m2m1m2m1m2 c1m1c2m2c1m1c2m2c1m1c2m2 c1c2c1c2c1c2 m1m2m1m2m1m2
m2 c2m2 c2m2

So the elements of the generating group G are, in the resulting colored symmetry group G* associated with, respectively, the permutations :

c1
c1c2
c2c1c2c1c2
c1c2c1c2
c2c1c2
c1c2c1c2c1c2
c2

We will now determine the periods of these seven permutations.

So in total the periods of the permutations are distributed as follows :

Five permutations of period 2
Two of period 4

Together with the identity permutation they have the fingerprint of a group with structure D4.
So we can say that the permutation group  PN = P4 ,  involved in the color symmetry group, has the structure of  D4 .

We will now tabulate the elements of the generating group  G  (with structure D4 ), their periods (as determined earlier), the permutations associated with those elements and their periods, and the elements of the colored symmetry group  G*  and their periods. And this table will at the same time demonstrate that the colored symmetry group has the same structure as the generating symmetry group from which it is derived, i.e. that the two groups  G  and  G*  are isomorphic.

G per. permutation. per. G* per.
1 1 -- -- 1 1
m1 2 c1 2 c1m1 2
m1m2 4 c1c2 4 c1c2m1m2 4
m2m1m2m1m2 2 c2c1c2c1c2 2 c2c1c2c1c2m2m1m2m1m2 2
m1m2m1m2 2 c1c2c1c2 2 c1c2c1c2m1m2m1m2 2
m2m1m2 2 c2c1c2 2 c2c1c2m2m1m2 2
m1m2m1m2m1m2 4 c1c2c1c2c1c2 4 c1c2c1c2c1c2m1m2m1m2m1m2 4
m2 2 c2 2 c2m2 2

Each element of the colored symmetry group  G*  is a transformation of the following form :
First the corresponding symmetry transformation of the generating group G, followed by a color permutation. As can be seen in the table, the period of the symmetry transformation is, in all cases, equal to that of the corresponding color permutation, and that implies that the combined transformation -- the symmetry transformation followed by the corresponding color permutation -- has the same period as the symmetry transformation alone (and, consequently, also as the color permutation for that matter). And this means that the  colored symmetry group G*  has the structure of  D4 ,  just like that of the generating group G.

We can now depict this color symmetry group using the symbols A, B, C and D of the color permutations and interpreting them as colors. The color of the identity element (let us call this color A ) is changed according to the color transformations of the colored symmetry group  G* .  We must determine into exactly what colors it is changed. From the above we know that :

The permutation  c1  is (BD), and changes A into A.
The permutation  c2  is (AD) (BC), and changes A into D.
The permutation  c1c2  is (ABCD), and changes A into B.
The permutation  c2c1c2c1c2  is (AB) (CD), and changes A into B.
The permutation  c1c2c1c2  is (AC) (BD), and changes A into C.
The permutation  c2c1c2  is (AC), and changes A into C.
The permutation  c1c2c1c2c1c2  is (ADCB), and changes A into D.

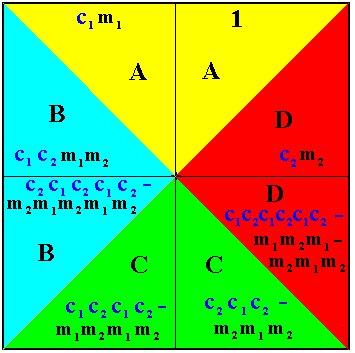
Figure 25.  Colored symmetry group  G* ,  derived from the group  G  (with structure D4 ) (Figure 22). Its eight elements are indicated in terms of the color permutations  c1  and  c2  and the symmetry generators  m1  and  m2 .  The colors are determined by the color permutations, and are indicated by the letters  A, B, C, D  and the corresponding colors themselves.
One of the significance of this case of colored symmetry (and of color symmetries in general) is the following :
If we look to Figure 25, and when we take the different colors into account, i.e. taking them as expressing certain correspondingly different features of the pattern depicted, and WITHOUT considering the theory of COLORED symmetry, we cannot detect any symmetry in the pattern, which means that it belongs to the symmetry group  C1 .
Nevertheless, we see, when looking to the pattern, one or another kind of regularity.
When we now involve the theory of colored symmetry, then we can indeed exactly specify the observed regularity :  The pattern belongs to the colored symmetry group  G*  with  D4  structure !
And all this can also be interpreted as follows :  The group G* is a desymmetrization of the group G (when we do not take the theory of colored symmetry into account).

The general symbol for a colored symmetry group involving an irregular permutation group -- as in our present case -- is G / H / H1 , where G is the generating group of colored symmetry.
And in our case H = {1, m1 }, which has the structure of  D1  (which is isomorphic to  C2 ). It is the subgroup that becomes highlighted in virtue of the color desymmetrization of the group G (As seen in Figure 22). The next Figure depicts this subgroup.

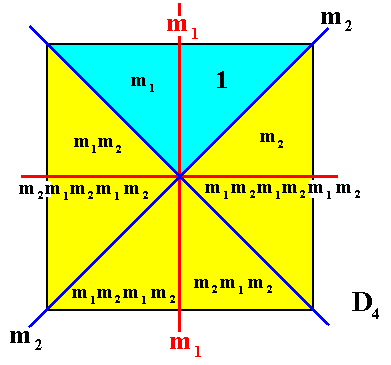
Figure 26.  The subgroup (blue)  H = { 1, m1 }  of the group  G .  It has  D1  structure.
H1 is in our case the subgroup {1}, i.e. the group consisting of the identity element only. We interpret it as the subgroup of G*. It is the subgroup which maintains each individual color unchanged.
So the symbol of our colored symmetry group is D4 / D1 / C1 .

And in this case the subgroup H emerging in virtue of the desymmetrization is not a normal subgroup of G, which can be checked as follows :
m2{1, m1 } is the left coset of H by the element  m2 ,  and is equal to  {m2, m2m1 }.
{1, m1 }m2 is the right coset of H by the element  m2 ,  and is equal to  {m2, m1m2 }.
And because (as we saw above)  m1  and  m2  do not commute, we have a case of the inequality of a right and left coset with respect to a certain group element, enough for knowing for certain that the subgroup is not normal (in G).
We will now expound a second example of a colored symmetry group with an irregular permutation group, but now involving a generating group which is infinite, namely the group  pmg ,  which is realized in certain friezes. In the foregoing, namely where we discussed this group with respect to its colored symmetry involving a regular permutation group, we already expounded some important features of it, so we can be concise.
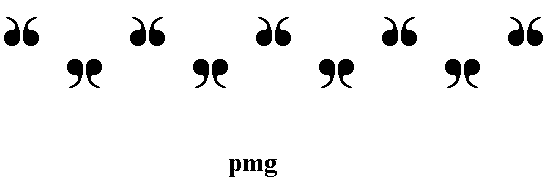
We first recapitulate some images depicting the group  pmg .

Figure 27.  A possible realization of the group  pmg .
The pattern must be imagined to extend indefinitely to the right as well as to the left.

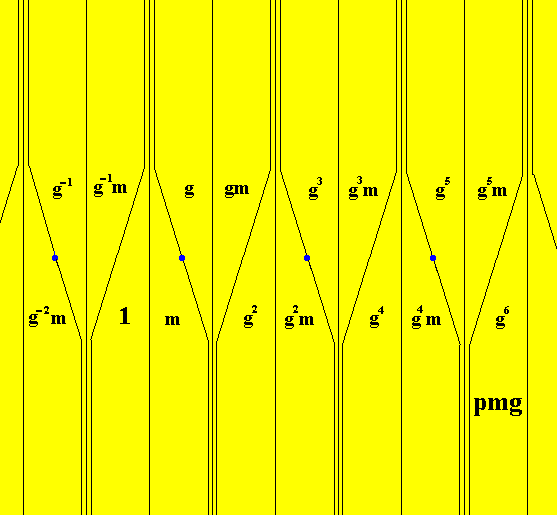
Figure 28.  The  pmg  pattern as plane tesselation by the orbit of the fundamental region, as established earlier. Each such area has the same color (yellow). The blue dots indicate the lattice nodes. Identities of the group elements are indicated.
The present case is a coloring with N = 3 colors, and the involvement of the irregular group  PN  and the subgroup H which is not a normal subgroup of the generating group  G = pmg . It demands the symbol  G / H / H1 . In this case also, besides the number N, the group of colored symmetry  G* ,  i.e. the corresponding color symmetry desymmetrization is uniquely defined by the generating group G, the stationary subgroup H of G*, which maintains every individual color unchanged and its symmetry subgroup  H1  which is the final result of the color symmetry desymmetrization. The index of the subgroup H in the group G is equal to N.
For the color desymmetrization of the group  pmg  we will use the system of colored generators {c1g, c2m}, i.e. we replace the generator  g  by the colored generator  c1g ,  and the generator  m  by the colored generator  c2m ,  where  g  is a glide reflection along the frieze axis, and  m  is a mirror reflection in a line perpendicular to the frieze axis (See Figure 28), and where  c1  is the permutation  (ABC), and  c2  is the permutation  (BC)  (both permutations in cycle notation).
We will now generate the corresponding colored symmetry group G* from the group G = pmg .  As some examples of the replacements to be performed, let us first perform the necessary replacements for the element  g2m.  The replacements result in the following :  c1gc1gc2m. And because the permutations commute with every element of the group G, we can write :  c12c2g2m .
Let us now take the element  g-1 .
g-1  must be replaced by  (c1g)-1 = g-1c1-1 = c1-1g-1 .
Further we see that
g-1m  must be replaced by  c1-1g-1c2m = c1-1c2g-1m ,  and
g-2m = g-1g-1m, which must be replaced by  c1-1g-1c1-1g-1c2m = c1-2c2g-2m .

With repect to the identity element  1  we can say the following :  1 = m2 ==> c2mc2m = c22m2 = c221 = 1 (because c22 is equal to the identity permutation). So, in applying the above specified replacements, 1 remains 1.

Figure 29.  Result of the replacement of symmetry generators by colored symmetry generators. The "c-part" and the "mg-part" (or "g-part") must be read together, so as to express a group element of the colored symmetry group  G* .
We will now look into the permutation group involved in the colored symmetry group. Let's list its elements (which are permutations of three colors, indicated by the letters A, B and C ).

So we have
One permutation of period 1 (identity element).
Two permutations of period 3.
Three permutations of period 2.
And this is the fingerprint of the group D3 ,  so the involved permutation group PN is  P3  with structure  D3 . And, as we can see, it contains permutations -- such as (AB) -- where an element remains unchanged, so the involved permutation group P3 is irregular.
Let's summarize these six color permutations :

c1 = (ABC)
c2 = (BC)
c12 = (ACB)
c22 = 1
c2c1 = (AC)
c1c2 = (AB)

From this we can determine that  c13 implies

A ==> B ==> C ==> A
B ==> C ==> A ==> B
C ==> A ==> B ==> C

and this is the identity permutation, so c13 = 1.

Further, c14 = c1, because the period of  is 3.

And, c15 = c12 .

Finally, c16 = 1.

The generator  g  will be replaced by  c1g  (and  m  by  c2m). So the transformation  g-1  must be replaced by  (c1g)-1 ,  which is equal to  g-1c1-1 = c1-1g-1 .
c1-1 is the inverse of  c1 ,  and this  c1  is the permutation (ABC) (cycle notation). So  c1-1  is the permutation (CBA), which is equal to (ACB), which is the permutation  c12 .
So  c1-1 = c12 , and  g-1  will be replaced by  c12g-1.

g-1m  must be replaced by  c1-1c2g-1m ,  which will now become  c12c2g-1m .

g-2 = g-1g-1 ,  and this will be replaced by  c12g-1c12g-1 = c12(g-1c12)g-1 = c12(c12g-1)g-1 = (c12)2g-2 = (c1)4g-2 = c1g-2 .
So  g-2  will be replaced by  c1g-2 .

g-2m = g-1g-1m  will be replaced by  c1-1g-1c1-1g-1c2m = c1-2c2g-2m .
Now c1-2 = c1-1c1-1 = c12c12 = (c1)4 = c1 .
So  g-2m  must be replaced by  c1c2g-2m .

On the basis of all this we can simplify the permutations as they were given in Figure 29 :

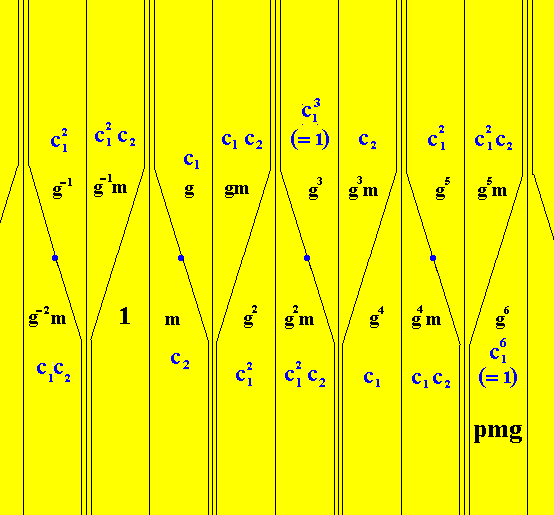
Figure 30.  The  pmg  pattern as given by the shape, position and orientation of the fundamental regions (i.e. the fundamental region and its copies).
In it the permutations are given, such that they effect the emergence of a color symmetry group (isomorph to the original group). The elements of the color symmetry group must be read as specified in Figure 29.
On the basis of these permutations (see the summary just made above), we can now determine the letters (representing colors), belonging to each region, starting from the letter  A  -- going to represent the color yellow -- which will be assigned to the region corresponding to the identity element  1 .
The permutations signify the color change from A into one of the other two colors (B or C), or into A :

c1 = (ABC) and implies A ==> B
c2 = (BC) and implies A ==> A
c12 = (ACB) and implies A ==> C
c22 = 1 and implies A ==> A
c2c1 = (AC) and impliees A ==> C
c1c2 = (AB) and implies A ==> B
c12c2 means
A ==> A ==> C
C ==> B ==> A
implying (AC), which is the permutation  c2c1, where
A ==> C.

See next Figure.

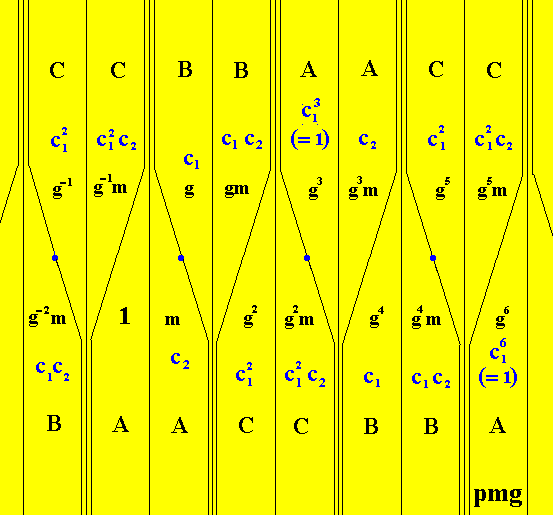
Figure 31.  Determination of the letters  A, B, C ,  representing colors, according to the color permutations.
We can now fill in the colors according to the letters in the previous Figure :

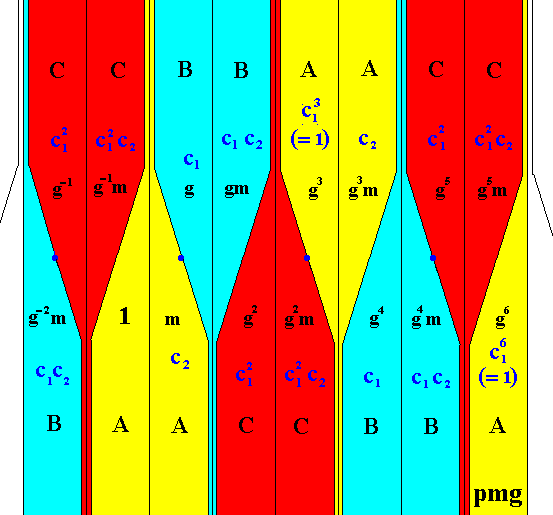
Figure 32.  Colored symmetry group  G*  derived from the group  G = pmg  by the color permutations  c1 = (ABC)  and  c2 = (BC) .
The colors are according to the letters, and these are according to the permutations involved.
The next Figure is the same as the previous one, but now with the markings omitted.

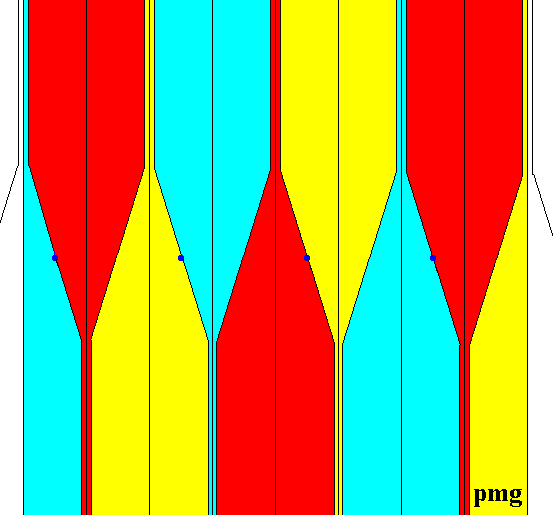
Figure 33.  Pattern representing the colored symmetry group  G*  as depicted in the previous Figure, but now with the markings omitted.
The stationary (no colors changed) subgroup H = { .  .  .  1,  c2m,  g3,  c2g3m,  g6  .  .  . } is represented by the yellow areas :

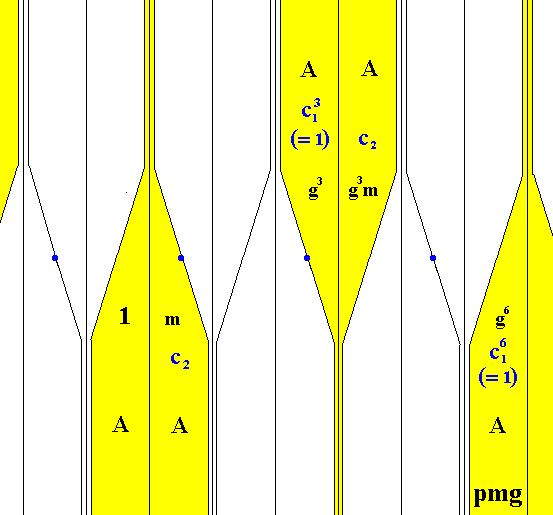
Figure 34.  The stationary subgroup H of the colored symmetry group  G* .
As can be seen in the above Figure, this subgroup H is isomorphic to the group  pmg  itself.

The symmetry subgroup H1  of G*, which is the final result of the color-symmetry desymmetrization, is {  .  .  .  c12g-1 ,  1,  c1g ,  c12g2 ,  g3 ,  c1g4 ,  c12g5 ,  g6 .  .  . }. See for it next Figure.

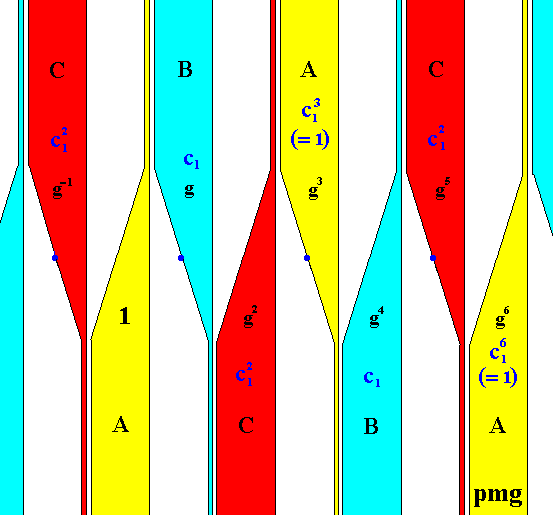
Figure 35.  The symmetry subgroup  H1  of the colored symmetry group  G* .
As can be seen from the above Figure, the subgroup H1 is isomorphic to the group  p1g ,  which is a frieze pattern generated by a glide reflection (See for this frieze, and all the others, the next document).
This concludes our exposition of the theory of antisymmetry groups and of colored symmetry groups (In the sequel we will make use of these theories).
Notation of symmetry groups

For friezes and ornaments we will use (and have already used) the international symbols (while for categories of groups we use the Bohm symbols explained above). These symbols consist of several parts.
The first part denotes the translational subgroup  p  (primitive lattice), or  c  (centered lattice) [ For two-dimensional lattices, see the first document of the Subseries on The Internal Structure of Crystals, namely the document The Five Fundamental 2-D Lattice Types, which you can find in the last Series of documents of the First Part of Website, accessible by  back to homepage ]
The other parts of such a symbol (coming after the first part) denote rotations, indicated by their highest period (for instance the symbol-part  4 ,  which denotes rotations of 900), and with their axes perpendicular to the plane of the frieze or ornament, and, further, mirror reflections  m  and glide reflections  g , perpendicular to those rotation axes, i.e. lying in the plane of the frieze or ornament.
While one usually uses small letters for the  p  c  (the translational subgroups) for friezes as well as for ornaments, we here will use capital letters when the group belongs to the ornaments (i.e. when it is one of the 17 Plane Groups), and small letters when the group is one of the 7 discrete line groups (which can be realized as friezes).
For example the group  P4gm  can be realized as a two-dimensional ornament (or can be interpreted as representing the total symmetry of a 2-dimensional crystal). As such it is a group of isometries in  E2  and belongs to the category  G2 ,  the symmetry group of ornaments (no invariant subspaces). The translational subgroup is based on a lattice that is primitive (i.e. the center of a unit mesh is not equivalent to its four corners). So this subgroup is denoted by  P  in the international symbol. Perpendicular to the plane of the ornament we find 4-fold rotation axes, denoted by the symbol  4 .  Further we find glide lines perpendicular to those rotation axes (and thus lying in the plane of the ornament), denoted by the symbol  g .  And, finally, we find reflection lines also lying in the plane of the ornament, denoted by the symbol  m .  So the total group symbol for this ornament is indeed  P4gm .
Analogously we can interpret the symbol  P4mm ,  relating to another symmetry type of ornament. A symbol like this is often presented in an abbreviated form, in this case as  P4m  (in fact as  p4m ). These abbreviated symbols omit symmetry elements that are implied by the others.
In the next document we will investigate the seven frieze patterns (Later they will figure as subgroups of the two-dimensional periodic patterns or ornaments).

e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology)

back to homepage

Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology

Back to subpatterns and subgroups (introduction)