The Symmetry of Two-dimensional Patterns

As prelude to the symmetry of three-dimensional crystals and organisms

Subpatterns and Subgroups Part I (Introduction)
e-mail : 

Overall Contents
1.  Subpatterns and Subgroups. Part I, Introduction.
2.  Subpatterns and Subgroups. Part II, Antisymmetry Groups, 
     Color Symmetry Groups.
3.  Subpatterns and Subgroups. Part III, Friezes. p11, p1g, pm1, p12
4.  Subpatterns and Subgroups. Part IV, Friezes. pmg, p1m, pmm
5.  Subpatterns and Subgroups. Part V, Friezes, ontology and
     significance.  Antisymmetry in friezes.  p11/p11, p12/p12, p12/p11, p1m/p1m, p1m/p11, p1m/p1g, pm1/pm1, pm1/p11, pmg/pm1.
6.  Subpatterns and Subgroups. Part VI,  Antisymmetry in Friezes.  pmg/p1g, pmg/p12, pmm/pmm, pmm/pm1, pmm/pmg.
7.  Subpatterns and Subgroups. Part VII,  Interpretation of
     motifs s.str. in plane group patterns.
     Difference between P31m and P3m1.
8.  Subpatterns and Subgroups. Part VIII,  Interpretation of
     motifs s.str. in plane group patterns (Sequel).
P1, P2, Pm, Pg, P2mm, P2mg, P2gg.
9.  Subpatterns and Subgroups. Part IX,  Interpretation of
     motifs s.str. in plane group patterns (Sequel).
Cm, C2mm, P4, P4mm, P4gm.
10.  Subpatterns and Subgroups. Part X,  Interpretation of
     motifs s.str. in plane group patterns (Sequel).
P3, P31m, P3m1, P6, P6mm.
11.  Subpatterns and Subgroups. Part XI,  Antisymmetry in
     Ornaments.  P1, P2
12.  Subpatterns and Subgroups. Part XII,  Antisymmetry in
     Ornaments.  Pm
13.  Subpatterns and Subgroups. Part XIII,  Antisymmetry in
     Ornaments.  Pm,  Ontology of Symmetry Groups.
14.  Subpatterns and Subgroups. Part XIV,  Antisymmetry in
     Ornaments.  Pg, P2mm.
15.  Subpatterns and Subgroups. Part XV,  Antisymmetry in
     Ornaments.  P2mm.
16.  Subpatterns and Subgroups. Part XVI,  Antisymmetry in
     Ornaments.  P2mm, P2mg.
17.  Subpatterns and Subgroups. Part XVII,  Antisymmetry in
     Ornaments.  P2mg, P2gg.
18.  Subpatterns and Subgroups. Part XVIII,  Antisymmetry in
     Ornaments.  P2gg.
19.  Subpatterns and Subgroups. Part XIX,  Antisymmetry in
     Ornaments.  P2gg.
20.  Subpatterns and Subgroups. Part XX,  Antisymmetry in
     Ornaments.  P2gg.
21.  Subpatterns and Subgroups. Part XXI,  Antisymmetry in
     Ornaments.  Cm.
22.  Subpatterns and Subgroups. Part XXII,  Antisymmetry in
     Ornaments.  Cm.
23.  Subpatterns and Subgroups. Part XXIII,  Antisymmetry in
     Ornaments.  C2mm.
24.  Subpatterns and Subgroups. Part XXIV,  Antisymmetry in
     Ornaments.  C2mm.
25.  Subpatterns and Subgroups. Part XXV,  Antisymmetry in
     Ornaments.  C2mm.
26.  Subpatterns and Subgroups. Part XXVI,  Antisymmetry in
     Ornaments.  C2mm.
27.  Subpatterns and Subgroups. Part XXVII,  Antisymmetry in
     Ornaments.  C2mm.
1aa.  Group Theory :  Sequel to Antisymmetry of Ornaments. (Subpatterns and Subgroups) ( In Sequel to Contents : LINK to Part XXVIII )
Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first  q, then  p, and then  a.
Sequel to Infinite two-dimensional periodic patterns
The present document, and the ones that follow, will go on with Group Theory, but with special emphasis on its application to the symmetries of two-dimensional patterns. As has been said, these patterns, especially the periodic ones, are instructive for an understanding of the total symmetry of real three-dimensional crystals, which are more complicated than such two-dimensional patterns. But, because we, on this website, also consider extensively the symmetries as they occur in organisms [To consult that, click HERE and then go to the documents concerning The Promorphological System, that come after those on Group Theory and those on (organic) Tectology], also other symmetries than those that occur in crystals must be considered.
The symmetries of crystals and their two-dimensional counterparts are so-called isometric symmetries, i.e. transformations that preserve distances. But in addition to such isometric symmetries, in organisms we also find similarity symmetries, in which distances are not preserved, but only angles and shapes,  and, so-called conformal symmetries, in which circles are preserved. These extra symmetries can help us refining our Promorphological Categories, i.e. refining our understanding of the symmetries as we find them in organisms. As a corollary, our group theoretic approach to two-dimensional patterns will give some insight in certain ornamental works of art in modern as well as in ancient times (Remember that art is often inspired by natural examples, and it is after all generated by organisms, namely humans).
After this treatment of two-dimensional patterns (periodic and non-periodic), we will concern ourselves with the symmetry theory of three-dimensional crystals, their point groups, lattices, and space groups.
And when all this has been done, we can then go (by means of a link) to the conclusion of our treatment of three-dimensional crystals (chemical lattice types, twins, and thermodynamics) and from there to the Tectology documents (concerning the general structure of organisms), and, finally, to the Promorphology documents (concerning the symmetries of organisms), via the Back to 3-dimensional crystals (conclusion), Organic Tectology, Promorphology link at the lower end of the left frame (A link that you can also find at the end of the present document).
Sub-patterns and subgroups

In the foregoing documents on Group Theory (See Group Theory (Parts I -- XXIV ) we considered the possibility to generate the group of an infinite periodic two-dimensional pattern by augmented motif units, instead of producing it by generator elements, i.e. by certain basic motif units. During the course of that we discovered several subpatterns that turned out to be either subgroups or their cosets. We saw this in the groups  P6mm,  P3m1  and  P31m.  It is perhaps instructive to elaborate a little further on this subject of subpatterns.

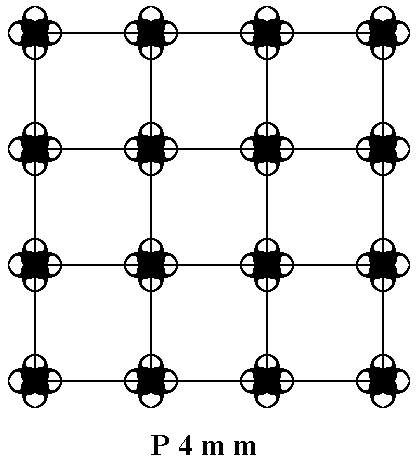
Let's consider a pattern representing Plane Group P4mm (Which is treated in Part XX of Group Theory) :

Figure 1.  Placing 2-dimensional motifs with point symmetry 4mm into a square 2-dimensional point lattice yields a pattern that represents the Plane Group P4mm. The pattern must be conceived as extending indefinitely in two-dimensional space ( E2 ).
Each (composed) motif of the pattern, as depicted in the above Figure, consists of eight motif units, which are commas. Such a comma looks like this :

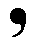
These eight commas together (and partly overlapping) form a composed motif having a 4mm symmetry. This symmetry, i.e. the symmetry of a single composed motif, can be described by (i.e. has the structure of) the group D4 .
Each motif unit (comma) represents a group element (of the group P4mm).
If we want to generate the pattern from a motif unit (comma), it can be done by selecting a set of possible generator elements. And this can be done in several ways, i.e. by several chosen sets of generators. For example the  P4mm  pattern can be generated by four generator elements :

An element  a  resulting from reflecting the initial motif unit in a mirror line  a .
An element  b  resulting from reflecting the initial motif unit in a mirror line  b  perpendicular to the line  a .
An element  g  resulting from subjecting the initial motif unit to a glide line (glide reflection) in a glide reflection line  g  at 450 to the line  a .
An element  t  resulting from the initial motif unit by a horizontal translation  t .

The pattern can also be generated by applying two translations to the composed motif, i.e. the full motif

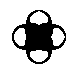
Had one taken, instead of the composed motif, consisting of eight commas, that part of it that consists only of two commas :

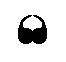
we could have generated the P4mm pattern by just a half-turn and a quarter-turn, situated as follows :

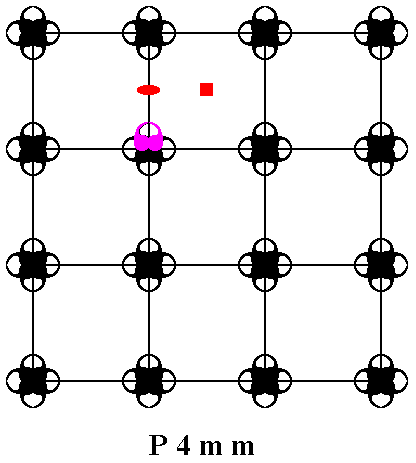
Figure 2.  By using a half-turn (indicated as a small ellipse) and a quarter-turn (indicated as a small square) at the positions indicated, the  P4mm  pattern can be generated from the initial motif unit (purple).
Larger motifs, such as

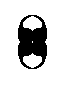
or

might also have been selected to generate the P4mm pattern.
Now the selection of a larger motif will always correspond to a subgroup of the full group of symmetries of the pattern, provided the symmetries of such a basic unit (i.e. the selected larger motif, consisting of more than one motif units) are symmetries of the pattern as a whole :
For example in Figure 1, each motif of the form

has D4 symmetry, and the pattern is the same, in effect, as a pattern of square motifs, i.e. motifs of the form

arranged with their centers forming a square lattice (as we see such a lattice in Figure 1). Now if these motifs were all given a rotation through 450, we should still have  P4mm ,  but if they were rotated through, say, 300, we should merely have  P4  :  Each motif would still possess its individual D4 symmetry, but of these symmetries only the half-turns, quarter-turns and three-quarter-turns would belong to the symmetries of the whole pattern so obtained. And because the other symmetries (namely the mirror lines) of the D4 symmetries do not belong to the full group (so obtained), these D4 symmetries cannot form a subgroup of the full group, which is now the group P4.

The next Figure shows such a square lattice provided with 300 rotated square motifs.

Figure 3.  A square point lattice (indicated by auxiliary lines, such that the lattice points coincide with the intersection points of those lines). Each point of the lattice is provided with a square motif that is rotated 300 with respect to the lattice lines. Because of the insertion of these rotated square motifs in the square net, the latter looses all its mirror lines. Only the rotations ( 900, 1800 and 2700 ) of the square motifs belong to the whole pattern. Consequently those square motifs do not represent D4 subgroups (or, more exactly, a D4 subgroup and its cosets) of the whole pattern. In virtue of all this the latter is a  P4  pattern.
So, provided the symmetries of the chosen larger motif (i.e. a motif consisting of more than one motif unit) with which we generate the P4mm pattern, are symmetries of the pattern as a whole, such a larger motif corresponds to a subgroup of the full group of symmetries of the pattern. For example the subgroup D1 ( =  C2 ) {1, at} :

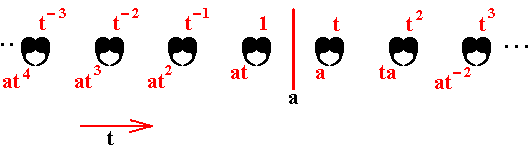
Figure 4.  Generating the  P4mm  pattern. Addition of yet another (horizontal) mirror line and a glide line (at 450) will generate the whole pattern.
with the table :

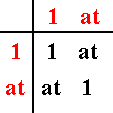
corresponds to the choice of

which can be used as augmented motif unit to generate the  P4mm  pattern.
The choice of the subgroup {1, a, b, ab} corresponds to

The next Figure explains this by taking a part of Figure 4.

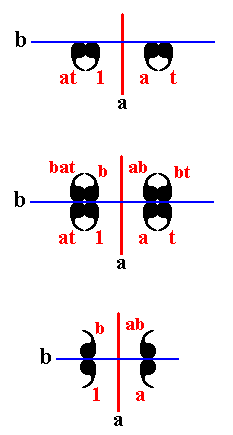
Figure 5.  Addition of the mirror line  b  in order to generate the  P4mm  pattern.
The resulting augmented motif unit, as depicted in the bottom image of Figure 5, indeed represents the subgroup {1, a, b, ab} with symmetry group D2 . And, qua symmetry this motif unit is equivalent to

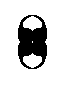
which also can be found in the P4mm pattern (See Figure 1), and which also has the structure of the symmetry group D2 . Here  a  and  b  correspond to two mirror lines perpendicular to each other, which indeed are to be found as symmetries of the whole  P4mm  pattern. The symmetries are situated as follows :

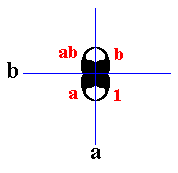
In addition to these mirror lines, both versions of augmented motif unit possess an implied 2-fold rotation axis in their center. Also this symmetry is present in the P4mm pattern, and is equivalent to the transformation  ab (= ba).

And, of course, the choice of the subgroup {1, p, p2, p3, m, pm, p2m, p3m} corresponds to

where the elements are situated as follows :

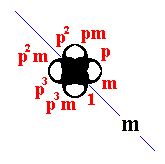
and where the symmetries  p  (anticlockwise rotation of 900) and  m  (reflection in the mirror line  m ) are indeed symmetries of the whole  P4mm  pattern.
Let's now investigate a pattern according to the plane group  P2mm .

Figure 6.  Two-dimensional periodic pattern according to the plane group  P2mm .
The pattern must be imagined to extend indefinitely in two-dimensional space ( E2 ).
As generators we can choose four mirror lines  a, b, c,  and  d :

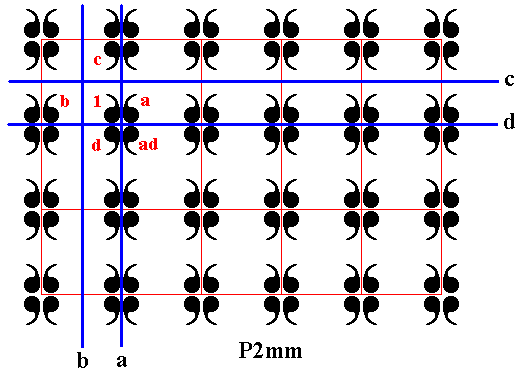
Figure 7.  The  P2mm  pattern. Four generators, the reflections  a, b, c, d ,  indicated. The elements  1, a, d, ad  -- and the corresponding motif, consisting of 4 commas -- form the subgroup  {1, a, d, ad}  with structure  D2 .
That two parallel mirror lines effect a translation is shown by the next Figure.

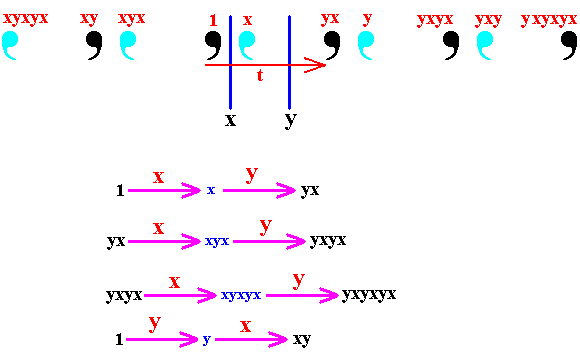
Figure 8.  Two parallel reflections result in a multiplication of a motif in a direction perpendicular to the reflection lines :  When we reflect a motif in one such mirror line and reflect it immediately in the second mirror line, the final image is then related to the very first motif as its translation perpendicular to the mirror lines.
And because (Figure 7) we had as generators a set of two parallel mirror lines, and another such set perpendicular to it, we have in fact two translations perpendicular to each other. And when these mirror lines are properly placed, as in Figure 7, we can indeed generate the whole pattern by means of these four reflections.

The  D2  structure of the subgroup  {1, a, d, ad}  (Figure 7) and of the corresponding motif

can be made explicit by its group table :

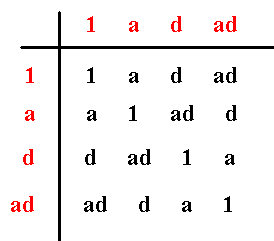
Figure 9.  Group Table of  D2 .
When we now subject this  D2  motif to two translations perpendicular to each other, we generate the whole  P2mm  pattern.

Now it is quite possible to generate a plane pattern by an 'infinite motif', i.e. to have a sub-pattern containing an infinite number of commas, and such a sub-pattern would correspond to an infinite subgroup. For example, in  P2mm ,  the subgroup generated by a vertical and a horizontal translation,  ab  and  cd ,  is as such a  P1  pattern. See next two Figures.

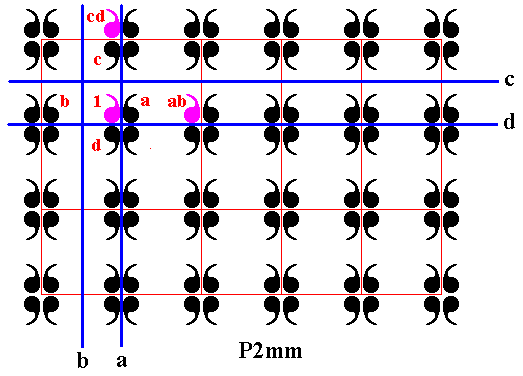
Figure 10.  In the  P2mm  pattern of Figure 6 the element  ab  (reflection  b  followed by reflection  a ),  which (combined transformation) is equivalent to a horizontal translation, is indicated. Also the element  cd  (reflection  d  followed by reflection  c ),  which (combined transformation) is equivalent to a vertical translation, is indicated. These two translations, when -- beginning with element  1 -- repeatedly applied, generate the subgroup  P1 . See next Figure.

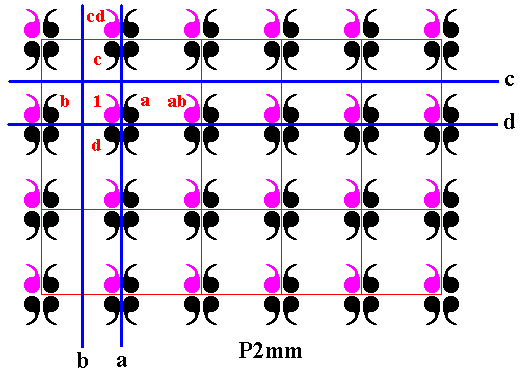
Figure 11.  The subgroup  P1  (purple) (of the group P2mm) generated by the translations  ab  and  cd  (and their inverses  (ab)-1  and  (cd)-1 ).
Indeed, an asymmetric motif, repeated by applying two differently directed translations, i.e. two translations making an angle smaller than 1800, results in a  P1  pattern.

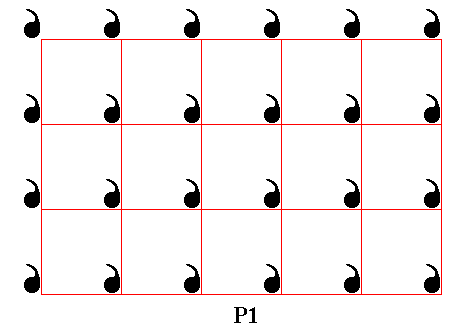
Figure 12.  The subgroup  P1  isolated.
From this  P1  'motif' -- i.e. from the whole  P1  pattern considered as one motif, one infinite motif -- we can generate the whole group  P2mm by means of two reflections perpendicular to each other and their axes correctly placed.

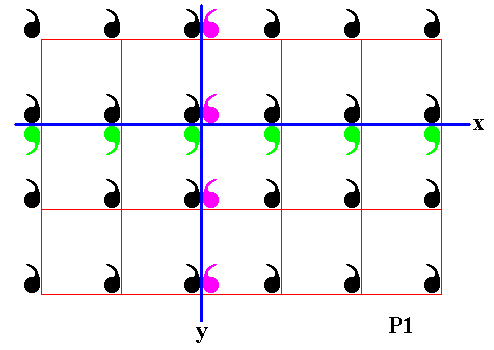
Figure 13.  The subgroup  P1  -- as ' infinite motif ' -- is subjected to two mirror lines,  x  and  y . In order to highlight these mirror lines, some of their images are indicated, i.e. a partial image of the subgroup under these reflections, is shown. See next Figures.
So our  P1  pattern can be seen as an infinite motif, and as such, as the initial motif for generating the  P2mm  pattern. This time the generating symmetry elements -- two mirror lines,  x  and  y ,  perpendicular to each other -- run right through the motif. The next Figures show the subjecting of this infinite motif to the mirror reflection  y .

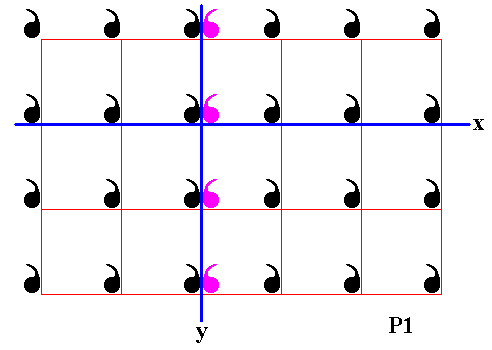
Figure 14.  Third column of displayed part of (infinite)  P1  pattern is reflected in the mirror line  y .

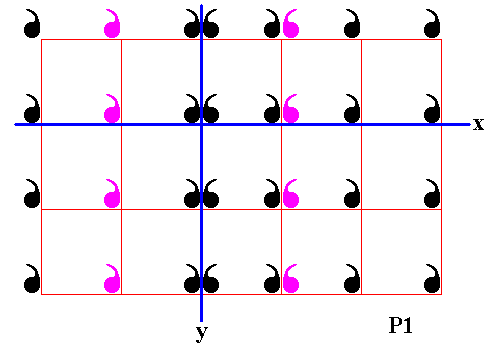
Figure 15.  Second column of displayed part of (infinite)  P1  pattern is reflected in the mirror line  y .

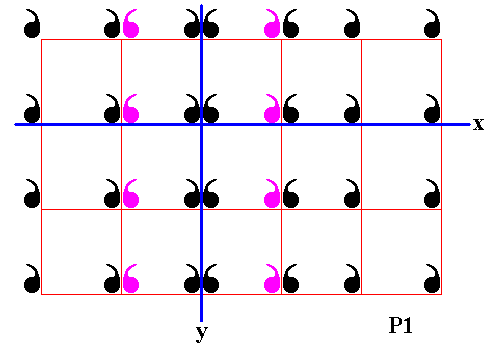
Figure 16.  Fourth column of displayed part of (infinite)  P1  pattern is reflected in the mirror line  y .

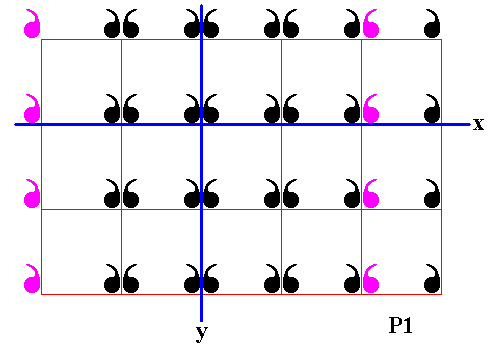
Figure 17.  First column of displayed part of (infinite)  P1  pattern is reflected in the mirror line  y .

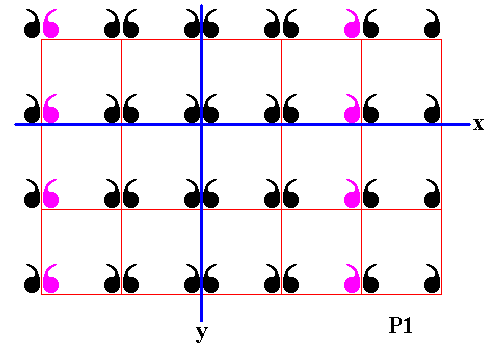
Figure 18.  Fifth column of displayed part of (infinite)  P1  pattern is reflected in the mirror line  y .
In this way the action of the mirror line  y  leads to the generation of more and more columns from existing columns (only part of which was displayed) :

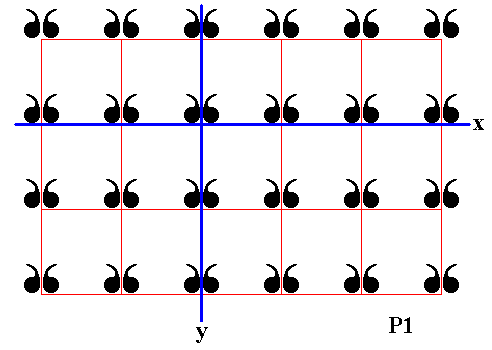
Figure 19.  Final result of the reflection of the displayed part of the  P1  pattern in the mirror line  y .
This result will now be reflected in the mirror line  x .  See next Figures.

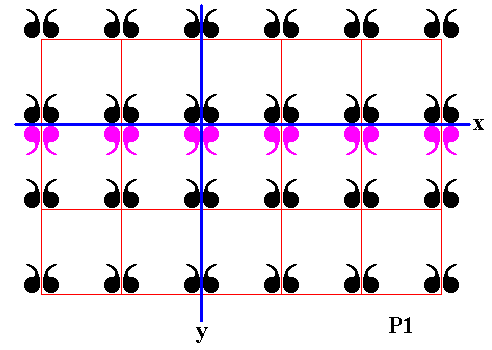
Figure 20.  Second row of displayed part of (infinite)  P1  pattern is reflected in the mirror line  x .

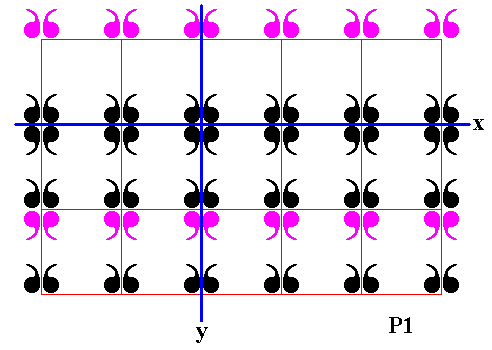
Figure 21.  First row of displayed part of (infinite)  P1  pattern is reflected in the mirror line  x .

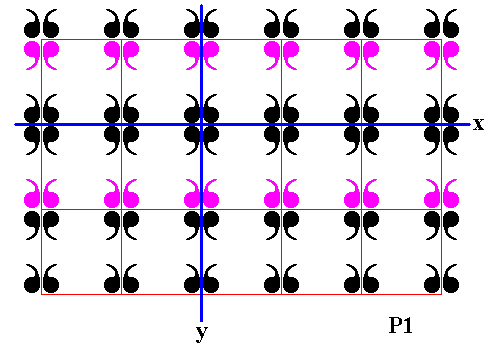
Figure 22.  Third row of displayed part of (infinite)  P1  pattern is reflected in the mirror line  x .
In this way all existing rows will be reflected in the mirror line  x :

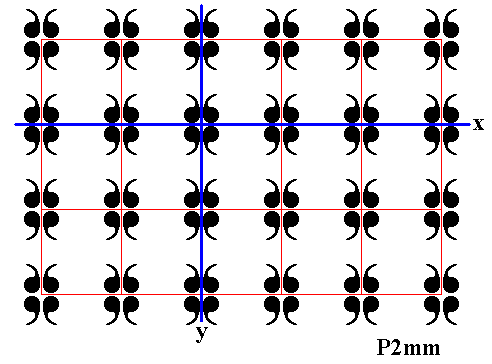
Figure 23.  Final result of the reflection of the displayed part of (infinite)  P1  pattern in the mirror lines  x  and  y ,  resulting in a pattern according to the plane group  P2mm .
So we have now generated the whole  P2mm  pattern by subjecting the infinite motif  P1  (which is a subgroup of P2mm) to the reflections  x  and  y .
In the next document we will continue our study of subpatterns and subgroups of two-dimensional periodic patterns. An important type of infinite subgroup (and corresponding subpattern) is represented by the friezes (rim ornaments, border ornaments, strip patterns), i.e. the one-dimensional counterparts of two-dimensional periodic patterns (plane ornaments, wall-paper patterns).
Generally, the study of subgroups and subpatterns is instructive for the phenomenon of symmetry-breaking or desymmetrization, which occurs in (the course of) some natural processes.

e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography), and the basic symmetry in organisms (promorphology).

back to homepage

back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology