2-D patterns XXV

The Symmetry of Two-dimensional Patterns

As prelude to the symmetry of three-dimensional crystals and organisms

Subpatterns and Subgroups Part XXV (Subgroups and Antisymmetry in Ornaments)

e-mail :

Sequel to Group Theory

As always, we start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.

Infinite two-dimensional periodic patterns, or Ornaments (sequel)

In the previous documents we investigated antisymmetry, subpatterns and subgroups of the plane group C2mm. Here we will give some examples of antisymmetry patterns, derivable from C2mm patterns, and present in Neolithic ornamental art.

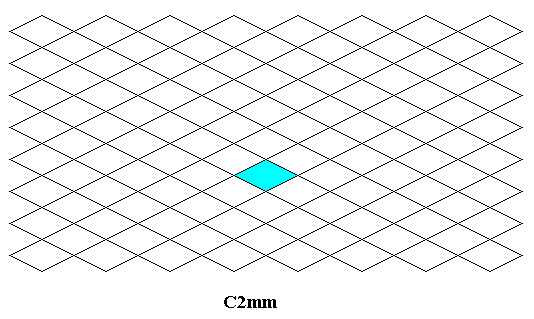
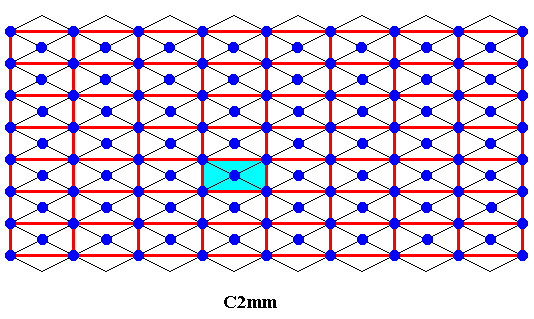
Figure 1. Generating C2mm pattern, from which an antisymmetry pattern (C2mm / P2mm, Figure 26 ) can be derived that is found in Neolithic art. The lines are the motifs of the pattern and at the same time indicate its rhombic point lattice. A unit mesh is indicated.

Let's first analyse this pattern.

NOTE :
In the following ( Figures 2--25 ) we analyse the C2mm pattern of Figure 1. We show the two different unit meshes associated with the two possible point lattices for any C2mm pattern, namely the rhombic lattice (with rhombic unit meshes) and the centered rectangular lattice (with rectangular unit meshes). We give two alternative ways of generating our C2mm pattern (which consists of oblique lines only), in order to enhance insight in the (algebraic) structure of C2mm patterns in general.
Because patterns representing the plane group C2mm are already investigated on many earlier occasions within this website, the reader might wish to skip the following analysis, to directly proceed further with the study of antisymmetry patterns. (Here the examples of such patterns derivable from C2mm patterns and present in Neolithic art). If he or she indeed wishes to do so, please click HERE .

As we have seen in the previous Figure, the repetition of the motifs of the pattern (which are its lines) can be described by a rhombic lattice. And because the motifs have a symmetry according to two perpendicular reflection lines which are also reflection lines of the whole pattern, the symmetry of the latter is indeed according to the plane group C2mm .
The repetition of the motifs can also be described by a centered rectangular lattice which is equivalent to the rhombic lattice :

Figure 2. Centered rectangular point lattice (indicated by the set of blue dots) of the above given generating C2mm pattern. A unit mesh is indicared.

Each mesh of the rhombic lattice consists of four group elements, as the next Figure shows.

Figure 3. Each unit mesh of the rhombic lattice consists of four group elements, because the content of such a unit mesh can be divided into four asymmetric units.

Each mesh of the centered rectangular lattice consists of eight group elements :

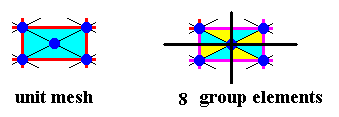
Figure 4. Each unit mesh of the centered rectangular lattice consists of eight group elements, because the content of such a unit mesh can be divided into eight asymmetric units. As one can see, these are the same units as occur in the rhombic meshes.

Let us generate the above C2mm pattern by first generating the content of a unit mesh of the centered rectangular lattice, and then generate more elements by (again) applying the generating half-turn, then using the generating reflections again, etc. Recall that our C2mm pattern under investigation only consists of oblique lines and no other features. See Figure 1.

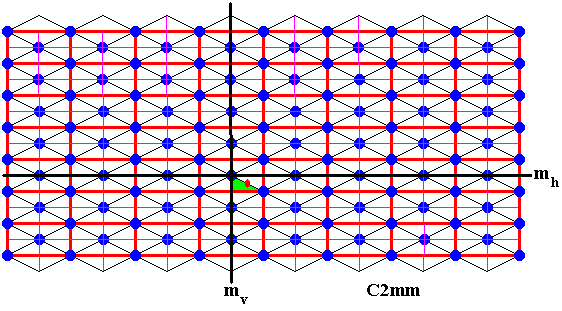
Figure 5. The identity element (green) and three generators for the above C2mm pattern are given. These generators are :

A half-turn about the point indicated by a small solid red ellipse. We will call it the generating half-turn.

A horizontal reflection in the line m_h .
A vertical reflection in the line m_v .

Strong red lines and blue dots indicate the centered rectangular point lattice (It doesn't belong to the pattern, but only describes the repetition of motifs).
Black thin oblique line segments are the motifs of the pattern.
These black thin oblique line segments, together with the thin purple line segments and the lattice lines (red), are boundaries of the areas (right-angled triangles) representing group elements.

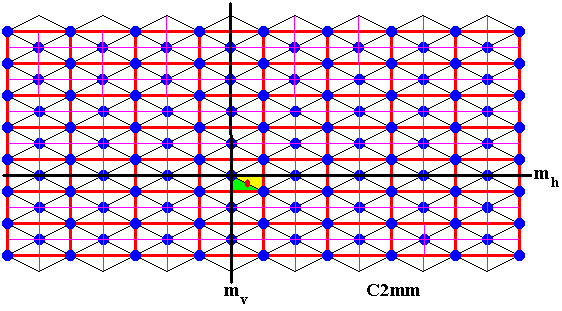
Figure 6. The generating half-turn creates a new element (yellow).

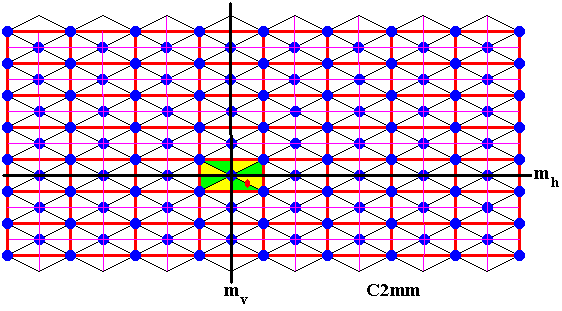
Figure 7. The rest of the elements of the unit mesh are generated by the horizontal and vertical reflections m_h and m_v .

Figure 8. Two more elements are generated by the generating half-turn.

Figure 9. Again two more elements are generated by the generating half-turn.

Figure 10. Yet again two more elements are generated by the generating half-turn.

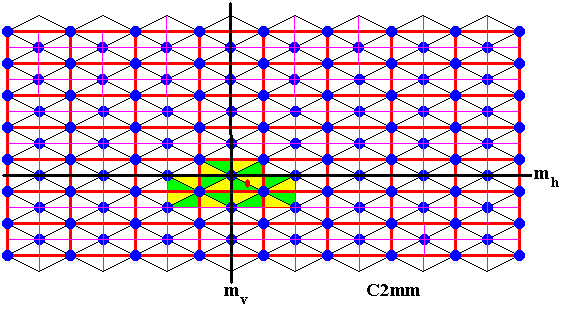
Figure 11. More elements are generated by reflection in the line m_v .

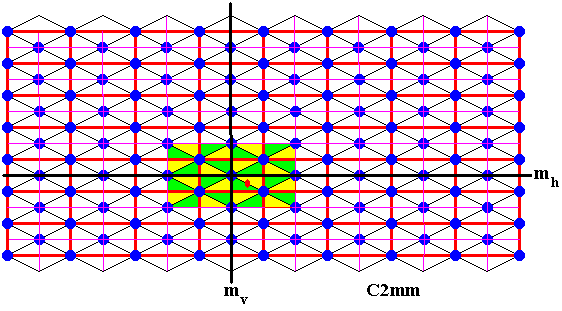
Figure 12. Still more elements are generated by reflection in the line m_h .

Figure 13. Two more elements are generated by the generating half-turn.

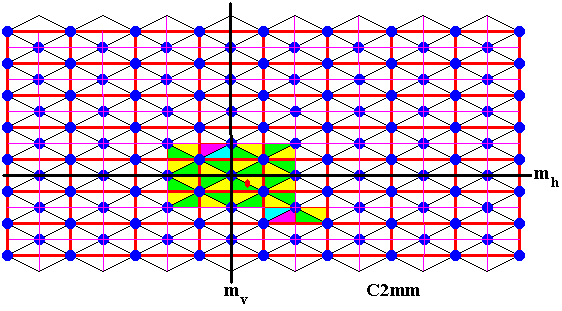
Figure 14. Again two more elements are generated by the generating half-turn.

Figure 15. Yet again two more elements are generated by the generating half-turn.

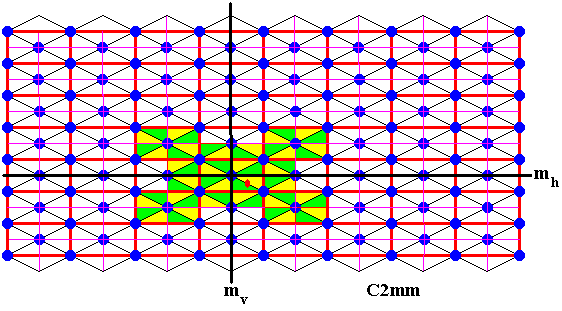
Figure 16. Still more elements are generated by the horizontal and vertical reflections in the lines m_h and m_v .

It is clear that continuing in this way the whole C2mm pattern can be generated (although the group is infinite).

As the pattern is generated with the three mentioned generators, viz. reflection in the line m_h , reflection in the line m_v and a half-turn in the point indicated in the above Figures by a small red solid ellipse, we can see that more symmetries are now implied. See next Figures.

Figure 17. Apart from the horizontal reflection line m_h another one is implied : m_hh . Indeed many more such lines are implied (in fact an infinity of them).

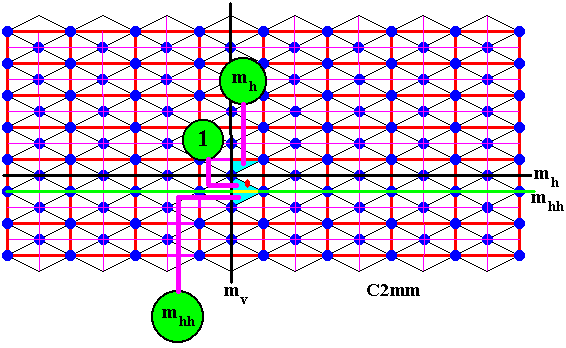
Figure 18. The areas representing the group elements 1, m_h and m_hh , i.e. the identity element, the horizontal reflection in the line m_h and the implied reflection in the line m_hh , are indicated.

Also a SE translation is implied in our C2mm pattern :

Figure 19. Implied SE translation in the C2mm pattern of Figure 1. If we take the area representing the identity element to be the green area, then the area representing the SE translation is the purple area (i.e. the area indicated by purple coloring). The other coloring only serves to highlight this SE translation, as it is implied in the pattern.

We will now (again) generate our C2mm pattern, in an alternative way, by means of the generators m_v , m_hh and t_se , i.e. the reflection in the vertical line m_v , the reflection in the horizontal line m_hh and the South-East translation. We will first generate the content of the unit mesh of the rhombic lattice (which, like the centered rectangular lattice, describes the repetition of motifs of our C2mm pattern [Figure 1 ] ), and then apply the SE translation, followed by reflection and again the SE translation.

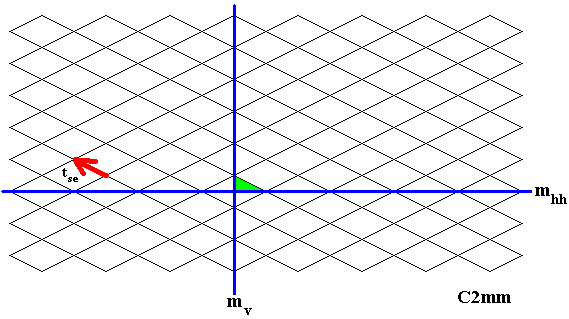
Figure 20. Alternative generation of the C2mm pattern of Figure 1.
The identity element (green), the reflection line m_v , the reflection line m_hh and the SE translation are given. See next Figures.

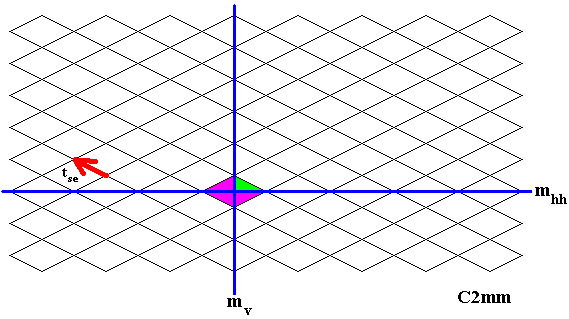
Figure 21. Alternative generation of the C2mm pattern of Figure 1.
The remaining group elements of the unit mesh are generated by the horizontal and vertical reflections m_hh and m_v .

Figure 22. Alternative generation of the C2mm pattern of Figure 1.
The elements of the unit mesh are subjected repeatedly to the SE translation, yielding many more new elements.

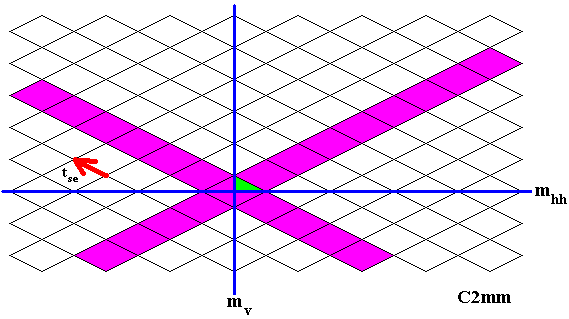
Figure 23. Alternative generation of the C2mm pattern of Figure 1.
Reflection in the line m_v of the elements already present, yields more elements.

Figure 24. Final stage in the alternative generation of the C2mm pattern of Figure 1.
Applying the SE translation repeatedly to the elements already present, completes the whole pattern.

Apart from the generating symmetry transformations used above to generate the C2mm pattern, some other symmetry transformations are automatically implied, among which the NE translation :

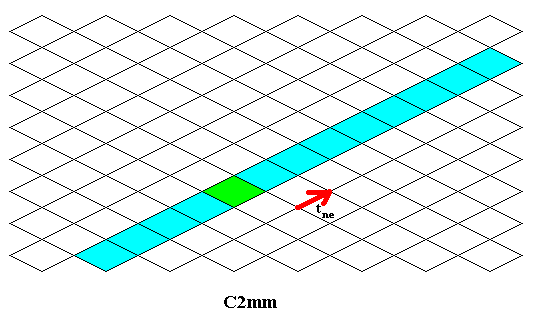
Figure 25. The implied NE translation of the C2mm pattern is indicated.

After having thus analysed the generating C2mm pattern of Figure 1, we now will derive from it the antisymmetry pattern as it is found in Neolithic art.
The neolithic antisymmetry ornament to be derived from the mentioned generating C2mm pattern can be obtained by replacing both the generating SE translation and the implied NE translation by their corresponding antisymmetry translations, where the antiidentity transformation e₁ will be interpreted as the color permutation (White Black) (cycle notation) with respect to the color of the interior of the rhombi of the pattern. The initial color is set to be white, as in Figure 1.
Because the generating reflections m_hh and m_v are not antisymmetry transformations, they will not involve color change. So the the identity element and the three other elements generated by these reflections, and together making up the content of a rhombus, will all be white. When we now apply the two antisymmetry translations (SE and NE) repeatedly to that (white) rhombus, we obtain color alternations (black--white), resulting in our neolithic antisymmetry ornament :

Figure 26. Antisymmetry pattern, as found in Neolithic art, derived from the generating C2mm pattern of Figure 1 , by replacing the SE and NE translations by their corresponding antisymmetry translations, where the antiidentity transformation e₁ is a color change as defined above. Identity element ( 1 ) and horizontal and vertical translations (arrows) indicated. These latter translations are ordinary symmetry transformations of the antisymmetry pattern. They are not a n t i s y m m e t r y translations, and do therefore not involve color changes.
(Adapted from JABLAN, 2002)

In order to correctly identify our just derived antisymmetry pattern, we isolate the set of white elements (including the identity element), and assess its symmetry.

Figure 27. Isolated subpattern (white elements, here highlighted by coloring them blue) of the above derived antisymmetry pattern.

The next Figure indicates the point lattice of the subpattern of the above derived antisymmetry ornament -- the set of white elements of the latter, now colored blue.

Figure 28. Point lattice (indicated by strong red connection lines) of the subpattern obtained from the above derived antisymmetry ornament (Figure 26 ). A unit mesh is indicated by alternative colors. The horizontal and vertical translations are shown by arrows. The lattice is a primitive rectangular net.

In the above Figure one can see that the subpattern consists of a D₂ motif (a rhombus) that is repeated according to two independent translations perpendicular to each other ( They are paralell to, and of the same length as, the sides of a lattice mesh). This demonstrates that the symmetry of the subpattern is according to the plane group P2mm .

We can see that the mentioned translations, inherent in the subpattern, are also symmetry transformations of the full group -- the generating C2mm group -- as well as of the antisymmetry group derived from it.

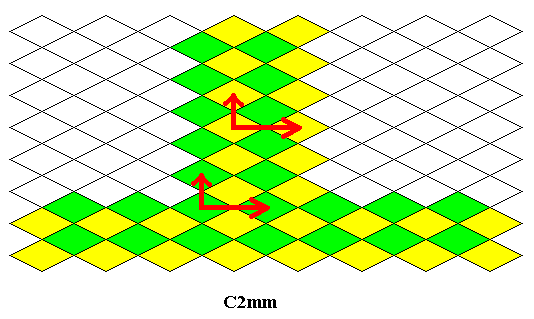
Figure 29. The generating C2mm pattern (full group of the subpattern).
Its vertical and horizontal translations indicated by two sets of vectors.

From the above Figure one can see that the vertical and horizontal translations of the subpattern (Figure 28 ) are also symmetry transformations of the generating C2mm pattern (Figure 29), and also of the antisymmetry pattern derived from it (Figure 26 ). Moreover the identity element is the same in all three groups. It is represented by a quarter of a rhombus.
All this demonstrates that the P2mm subpattern is a s u b g r o u p of the C2mm group representing the generating pattern, as well as of the antisymmetry group representing the neolithic antisymmetry ornament. Therefore the symbol of the latter must read C2mm / P2mm .

In the next document we will give some more examples of antisymmetry patterns, present in Neolithic art, and derivable from C2mm patterns.

e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology).

back to homepage

Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology

Back to subpatterns and subgroups (introduction)

Back to subpatterns and subgroups Part II

Back to subpatterns and subgroups Part III

Back to subpatterns and subgroups Part IV

Back to subpatterns and subgroups Part V

Back to subpatterns and subgroups Part VI

Back to subpatterns and subgroups Part VII

Back to subpatterns and subgroups Part VIII

Back to subpatterns and subgroups Part IX

Back to subpatterns and subgroups Part X