2-D patterns XXI

The Symmetry of Two-dimensional Patterns

As prelude to the symmetry of three-dimensional crystals and organisms

Subpatterns and Subgroups Part XXI (Subgroups and Antisymmetry in Ornaments)

e-mail :

Sequel to Group Theory

As always, we start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.

Infinite two-dimensional periodic patterns, or Ornaments (sequel)

In the previous documents we have investigated antisymmetry patterns, subpatterns representing-, and subpatterns not representing subgroups, all derivable from P2gg patterns.
In the present document we will investigate the Plane Group Cm in these respects.

Figure 1 shows the rhombic lattice, with a D₁ motif placed in each mesh, and as such representing the plane group Cm .

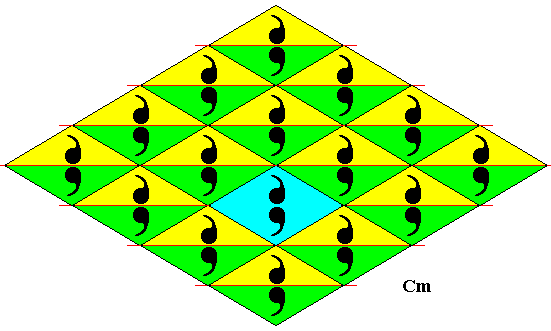
Figure 1. Pattern representing plane group Cm . The motifs s.str. are (chosen to be) a set of two commas, and as such placed inside the lattice meshes. The commas in a mesh are related to each other by a horizontal reflection line. Half of a rhombic lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit (comma) of the motif s.str. . A lattice mesh is indicated (blue). The pattern must be imagined to extend indefinitely over the plane.

We will derive antisymmetry patterns from the generating Cm symmetry pattern, where the antiidentity transformation e₁ will again be interpreted as the color permutation (Blue Red) (cycle notation) with respect to the background color of the pattern. We set the initial background color to be blue :

Figure 2. The Cm pattern of Figure 1, with the initial (background) color set to blue.

Figure 3. The Cm pattern of Figure 1, with the initial (background) color set to blue. The generating m i r r o r l i n e m is indicated (strong dark blue line). The area chosen to represent the identity element is indicated by the symbol 1 .

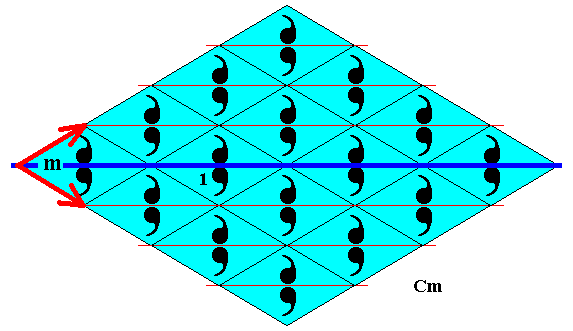
Figure 4. The Cm pattern of Figure 1, with the initial (background) color set to blue. The two generating t r a n s l a t i o n s are indicated by the corresponding vectors (red arrows).

The first antisymmetry pattern to be derived from the above generating Cm pattern can be obtained by replacing the generating mirror reflection in the line m by the corresponding antisymmetry transformation (antisymmetry reflection).

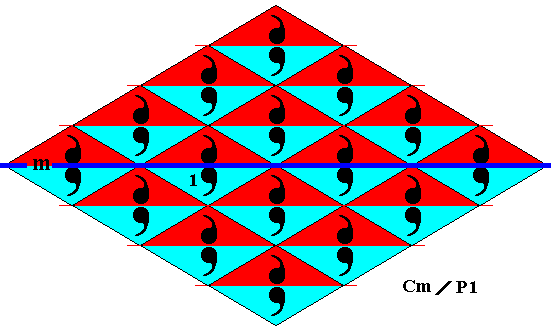
Figure 5. Antisymmetry pattern derived from the generating Cm pattern depicted in the previous Figures, by replacing the generating mirror reflection by its corresponding antisymmetry transformation.

If we look to the set of blue elements we see that it is a pattern consisting of an asymmetric motif that is translated along two independent directions, indicating that it is a P1 pattern. And because the translations involved are identical to those of the generating pattern it represents a subgroup of the latter. So the symbol of the antisymmetry pattern must read Cm / P1 .

The next Figures give the point lattice of the generating Cm pattern and that of the above derived antisymmetry pattern.

Figure 6. Point lattice (indicated by connection lines) of the generating Cm pattern.

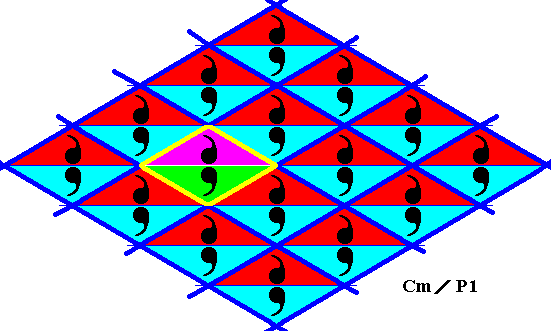
Figure 7. Point lattice (indicated by strong dark blue connection lines) of the above derived antisymmetry pattern. A unit mesh is indicated by yellow outline and alternative colors.

The next antisymmetry pattern can be derived from the generating Cm pattern by replacing one generating translation by its corresponding antisymmetry transformation, where the antiidentity transformation e₁ is still interpreted as the color permutation (Blue Red) (cycle notation) with respect to the background color. The next Figure gives the result.

Figure 8. Antisymmetry pattern derived from the generating Cm pattern depicted in Figure 2, by replacing one of the translations (indicated by a red arrow) by its corresponding antisymmetry transformation.

The next Figure isolates the blue elements of the just derived antisymmetry pattern.

Figure 9. Isolated subgroup (blue elements) of the above derived antisymmetry pattern (Figure 8). We can see that the mirror lines are no longer present, i.e. the pattern does not possess mirror symmetry, despite the fact that the motifs still have mirror symmetry. The only symmetry the pattern of blue elements possesses are two translations as indicated. These translations are also elements of the full group, i.e. the generating Cm pattern. Therefore the blue elements indeed form a subgroup of that pattern. The symmetry represented by this subgroup cannot be anything else than that of the plane group P1 .

The next Figure shows the point lattice of the just isolated subpattern.

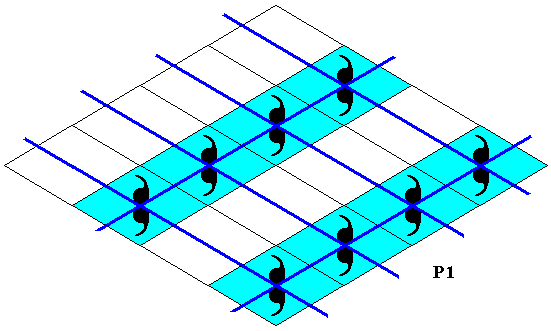
Figure 10. Point lattice (indicated by strong dark blue connection lines) of the just derived subpattern of blue elements. This lattice is an oblique net. The mirror symmetry (which is a non-translational symmetry) of the motifs does not have any relation with the symmetry of the whole pattern (which has no true non-translational symmetry at all).

Because the set of blue elements is a subgroup having P1 symmetry, the symbol representing the corresponding antisymmetry group (as was derived above) must read Cm / P1 .

The next Figures give the point lattice of the above derived antisymmetry pattern.

Figure 11. Point lattice (indicated by strong black connection lines) of the above derived antisymmetry pattern (Figure 8 ). Compare with the point lattice of the generating Cm pattern depicted in Figure 6.

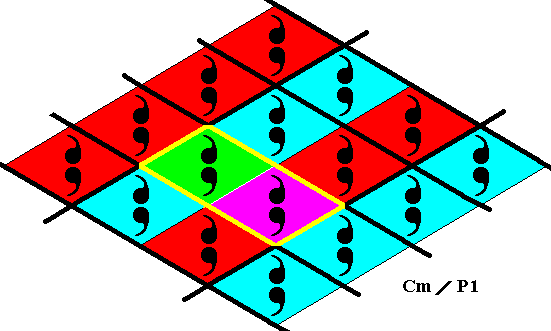
Figure 12. Point lattice (indicated by strong black connection lines) of the above derived antisymmetry pattern (Figure 8 ). A unit mesh is indicated by yellow outline and alternative colors.

The next antisymmetry pattern can be derived from the generating Cm pattern (Figure 2) by replacing one generating translation (indicated by an arrow in the next Figure) by its corresponding antisymmetry transformation and the generating reflection by its corresponding antisymmetry transformation :

Figure 13. Antisymmetry pattern derived from the generating Cm pattern by replacing one generating translation (red arrow) by its corresponding antisymmetry transformation and the generating reflection (in the line m ) by its corresponding antisymmetry transformation.

The next Figure isolates the subpattern consisting of the blue elements of the just derived antisymmetry pattern.

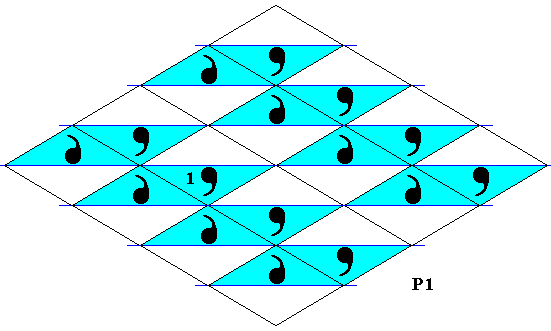
Figure 14. The set of blue elements of the above antisymmetry pattern isolated.

From the above Figure we can see that the subpattern of blue elements has P1 symmetry, but it is not a subgroup of either the antisymmetry pattern or the generating Cm pattern, because the area marked "1", which represents the identity element of the antisymmetry pattern as well as of the generating Cm pattern, is not an element of the alledged subgroup : From it we cannot generate the motif at the left of it. The pattern represents the plane group P1 of which the identity element must consist of both motifs taken together :

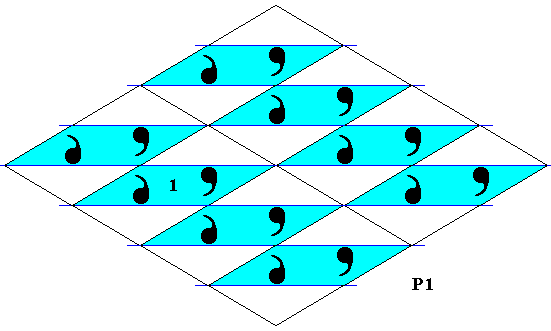
Figure 15. The set of blue elements of the above antisymmetry pattern has P1 symmetry but is not a subgroup of the antisymmetry pattern nor of the generating Cm pattern. Its proper identity element is indicated by the symbol 1 .

The next Figure gives this same P1 subpattern without superfluous lines, in order to let better stand out its symmetry.

Figure 16. The P1 subpattern of the above derived antisymmetry pattern, without superfluous lines.

The point lattice of this subpattern is indicated in the next Figure.

Figure 17. Possible point lattice (indicated by strong red connection lines) of the P1 subpattern of the above derived antisymmetry pattern Cm / *P1 (Figure 13 ). The true identity element (within the present choice of lattice) of the group, this pattern represents, is indicated by the symbol 1 (It is represented by the whole content of that unit cell).

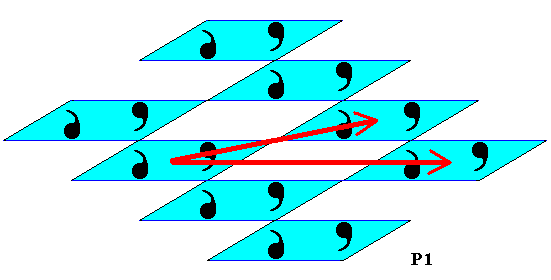
Figure 18. Alternative choice of generating translations of the P1 subpattern under discussion.

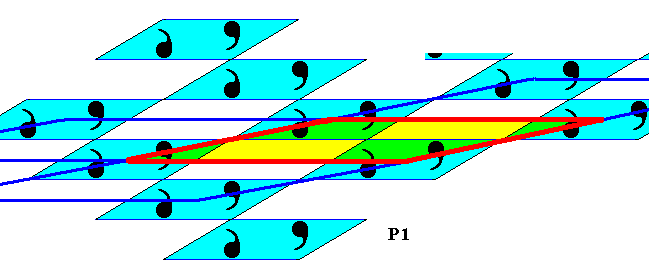
Figure 19. Unit mesh (indicated by strong red lines and alternative colors) of the above (Figure 18) given alternative choice of generating translations of the P1 subpattern under discussion. In a way, this choice of generating translations is more natural because within the motif of a mesh we don't see some parts of the motif related to each other by a symmetry transformation (and thus making the motif in all respects asymmetric, and as such now indicating a fundamental region), while in the first choice (Figure 17 ) that motif has parts related to each other by a translation. The whole content of this particular unit mesh (in the present Figure) can represent the identity element of the group P1 . The present choice of generating translations results in the smallest possible unit mesh (it is smaller than that resulting from the first choice).

Because the subpattern associated with the above derived antisymmetry pattern has P1 symmetry, and because it is not a subgroup of the antisymmetry pattern nor of the generating Cm pattern, the symbol for the antisymmetry group representing the derived antisymmetry pattern must read Cm / *P1 .

The next Figures show the point lattice of the above derived antisymmetry pattern.

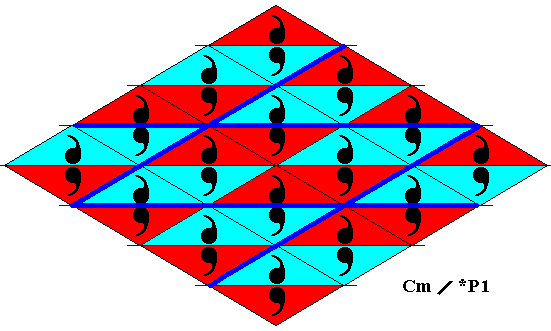
Figure 20. Point lattice (indicated by strong dark blue connection lines) of the above derived antisymmetry pattern (Figure 13 ).

Figure 21. Point lattice (indicated by strong dark blue connection lines) of the above derived antisymmetry pattern (Figure 13 ). A unit mesh is indicated by yellow outline and alternative colors.

The next three Figures indicate an alternative point lattice of the above derived antisymmetry pattern. It is preferable because its meshes are smaller.

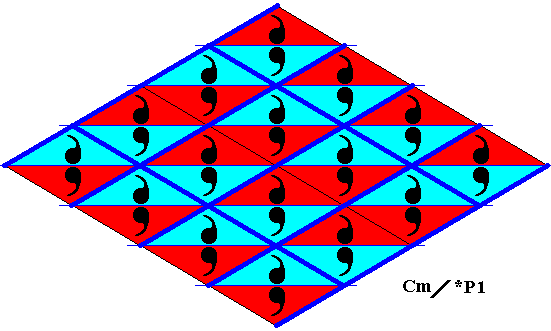
Figure 21a. Alternative and preferable point lattice (indicated by strong dark blue connection lines) of the above derived antisymmetry pattern. Its meshes are smaller than in the above Figures.

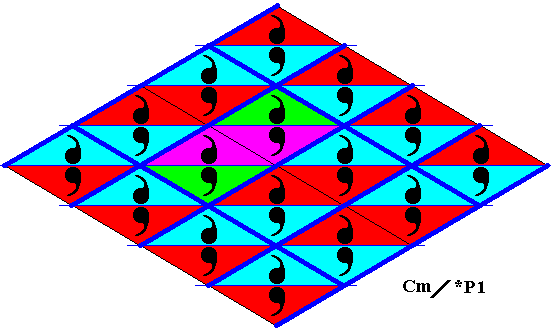
Figure 21b. Alternative and preferable point lattice (indicated by strong dark blue connection lines) of the above derived antisymmetry pattern. A unit mesh is indicated by alternative colors. It contains four motif units (commas), whereas the unit mesh of the other point lattice (Figure 21 ) contains eight motif units (commas).

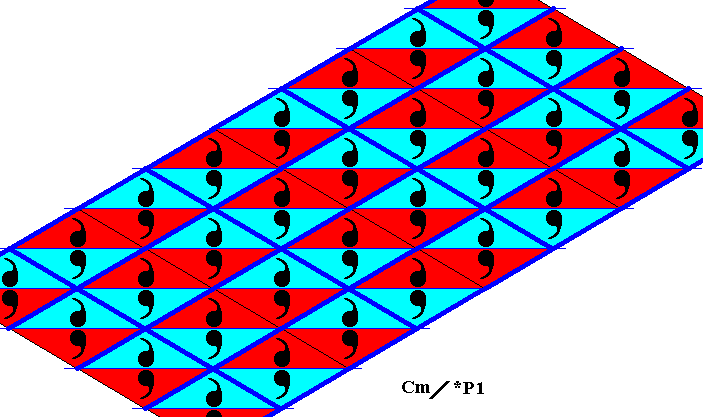
Figure 21c. Alternative lattice as in the two previous Figures. Pattern extended, in order to clearly see the periodic repetition of the unit mesh.

The next antisymmetry pattern to be derived from the generating Cm pattern (Figure 2 ) can be obtained by replacing both generating translations (See Figure 4 ) by their corresponding antisymmetry transformations, and the antiidentity transformation e₁ again signifying the color permutation (Blue Red) (cycle notation) with respect to the background color (which is initially set as blue).

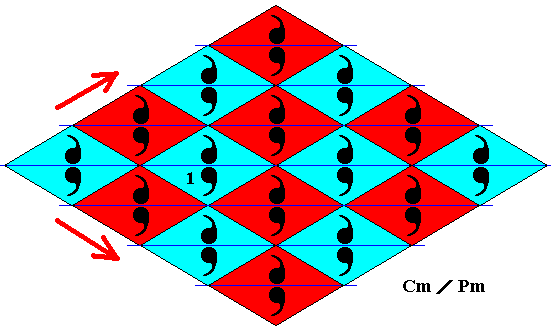
Figure 22. Antisymmetry pattern derived from the generating Cm pattern by replacing both generating translations (indicated by red arrows) by their corresponding antisymmetry transformations.

The next Figure isolates the subpattern consisting of the blue areas of the just derived antisymmetry pattern.

Figure 23. Subpattern, consisting of the blue elements of the just derived antisymmetry pattern, isolated.

Without superfluous lines the above subpattern looks like this :

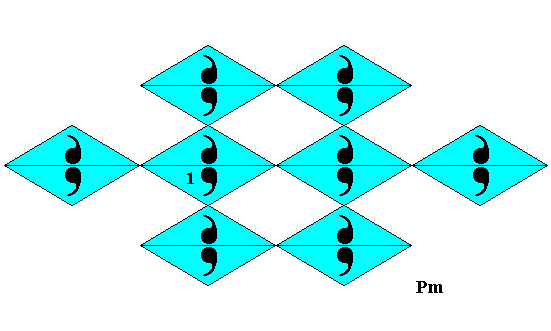
Figure 24. Subpattern, consisting of the blue elements of the just derived antisymmetry pattern, without superfluous lines.

The next Figure depicts the point lattice of the subpattern of blue elements.

Figure 25. Point lattice (indicated by strong red connection lines) of the subpattern consisting of the blue elements of the just derived antisymmetry pattern. It is a primitive rectangular lattice (where "primitive" means : lattice points only at the corners of the meshes). The two generating translations of the pattern are perpendicular to each other and can be represented by the sides of a rectangular mesh, or, equivalently, by the horizontal and vertical distances between the motifs (purple arrows).

The above Figure shows that the subpattern of blue areas is periodic. It further shows that we can generate the whole subpattern by first subjecting the area representing the identity element (1) to the horizontal generating reflection m . We have now two areas. If we subject these two areas repeatedly to the horizontal and vertical translations (as indicated by the sides of the lattice meshes) we obtain the whole pattern. Apart from horizontal reflections and the two translations perpendicular to each other, the pattern does not possess other symmetry transformations, indicating that its symmetry is that of the plane group Pm . And because the mentioned symmetry transformations are also symmetry transformations of the corresponding full groups (the antisymmetry group derived above and the generating Cm group, see next Figure), the subpattern of blue areas represents a subgroup of those full groups. Consequently the symbol for our above derived antisymmetry pattern must read Cm / Pm .

The next Figures show that the symmetry transformations of the subpattern of blue areas (two translations perpendicular to each other and horizontal reflections) are also symmetry transformations of the corresponding full groups (generating Cm pattern and Cm / Pm antisymmetry pattern).

Figure 26. The rhombic lattice of the generating Cm pattern (Figure 6 ) can be replaced by the (equivalent) centered rectangular lattice. In the present Figure this lattice is indicated by yellow dots (lattice points) and some auxiliary lines (red). And then we can see that the pattern has the two perpendicular translations found in the subpattern of blue areas (Figure 25 ). In both cases they are horizontal and vertical, while their length is equal to the distance between the centers of the motifs (double comma). In the generating Cm pattern (present Figure) we also see the horizontal reflection lines (one of them indicated by m ) which are also found to be present in the subpattern of blue elements (Pm) (Figure 25, one of them indicated by m ).

So the subpattern of blue elements -- itself having Pm symmetry -- is a subgroup of the generating Cm pattern.

The next Figures illustrate that the symmetry transformations of the subpattern of blue elements are also present in the full antisymmetry pattern, proving that it is a subgroup of the latter.

Figure 27. In the antisymmetry pattern as derived above we can detect two translations, vertical and horizontal. These translations are also symmetry transformations of the subpattern of blue elements (See Figure 25 ). Moreover in the antisymmetry pattern we can detect horizontal reflection lines also present in the sub-pattern of blue elements. These symmetry transformations (the mentioned translations [or equivalent choices of them] and the reflection lines) are the only symmetry transformations of the subpattern of blue elements. All this proves that the latter pattern is a subgroup of the group represented by the antisymmetry pattern.

The next Figure shows the point lattice of the above derived antisymmetry pattern as a result of the choice of generating translations in the previous Figure.

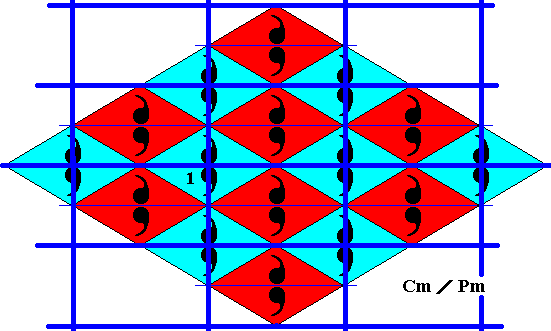
Figure 28. Point lattice (indicated by strong dark blue connection lines) of the above derived antisymmetry pattern, based on the choice of generating translations (Figure 27). The lattice is a rectangular net. It is not a centered rectangular net but a p r i m i t i v e rectangular net, because the central motif (present in each rectangular mesh) is not equivalent to the motifs at the four corners of the mesh, which means that the corresponding p o i n t s are not equivalent. So as a result of the present antisymmetry desymmetrization the c e n t e r e d rectangular lattice of the generating Cm symmetry pattern (Figure 26 ) has become a p r i m i t i v e rectangular lattice (present Figure).

The next two Figures show an alternative but equivalent lattice, an oblique lattice, of the above derived antisymmetry pattern (This lattice is also primitive).

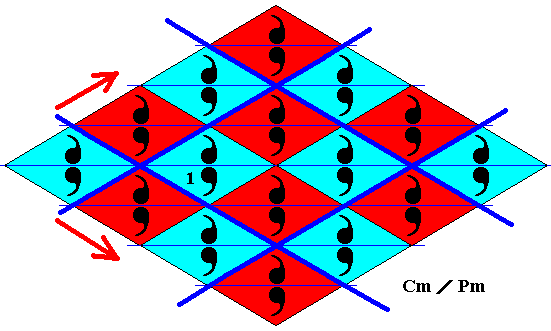
Figure 29. Alternative but equivalent point lattice (indicated by strong dark blue connection lines) of the above derived antisymmetry pattern, based on an oblique net. Both choices involve a mirror symmetric motif in each mesh. The primitive rectangular lattice of the previous Figure is more "natural" because it is smaller : each mesh contains 4 x 1/2 + 2 = 4 commas, while each mesh of the lattice in the present Figure contains 8 commas.

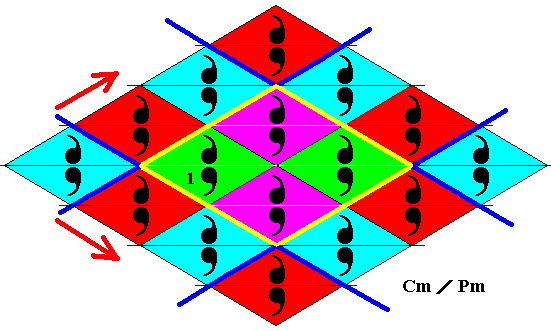
Figure 30. A unit mesh (indicated by yellow outline and alternative colors) of the lattice of Figure 29.

Subgroups

We will now show some patterns that represent subgroups of the plane group Cm not necessarily bound up with antisymmetry desymmetrizations (All periodic patterns must be imagined as extending indefinitely over 2-D space).
But before we do so we first consider the g e n e r a t i o n of the pattern representing the full group, i.e. the group Cm (Figure 6 ). We will generate it in several stages (Figures 31-34) by three generators :
Translation in the NE (north-east) direction.
Translation in the SE (south-east) direction.
Reflection in the horizontal line m .

Figure 31. Generation of the element m (purple) by reflection of the identity element (green, and indicated by 1 ) in the line m . This element m is itself a generator (a generator of itself as well as of other elements of the group). The two red arrows indicate the generating translations. Every comma (and its triangular background area) represents a group element.

Figure 32. Generation of some more elements by subjecting the elements already present by repeatedly applying the two generating translations.

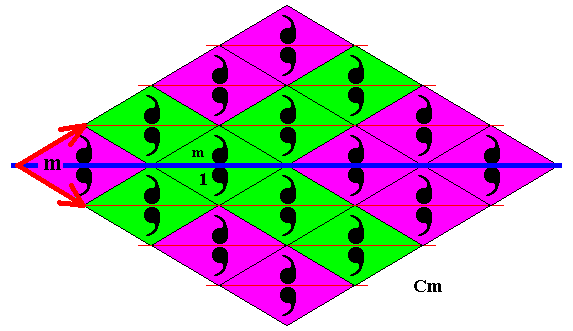
Figure 33. Generation of the rest of the (displayed) elements of the group Cm by applying the generating translations to the elements already present.

The above Cm pattern has as symmetry transformations :
The NE translations . . . t_ne^-1 , t_ne , t_ne² , t_ne³ . . .
The SE translations . . . t_se^-1 , t_se , t_se² , t_se³ . . .
Reflections in the horizontal lines as indicated in Figure 31.
Among these t_ne , t_se and the reflection in the line m are g e n e r a t o r s of the group Cm.
But all these elements are not the only elements : Two translations, one horizontal and one vertical, and their repetitions, are i m p l i e d , as shown in the next Figure.

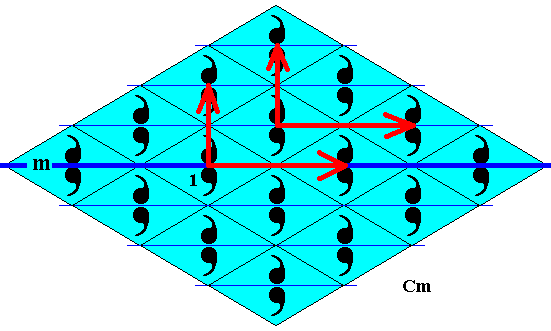
Figure 34. Two implied translations (indicated by red arrows) can be detected in the Cm pattern. One translation is vertical, the other horizontal.

The next Figure shows how one can generate the Cm pattern if one wants to use the horizontal and vertical translations (instead of the NE and SE translations) indicated in the previous Figure. It is then necessary to delineate the areas representing group elements differently.

Figure 34a. Generation of the Cm pattern (with centered rectangular lattice shown), using the horizontal and vertical translations (which are determined by the sides of the meshes of the centered rectangular net). Area representing the identity element is indicated (yellow). The line m (red) is chosen to represent the generating reflection. When we reflect the (area representing the) identity element in the line m we have two elements (1, m) . If we now subject these two elements to the horizontal and vertical translations, we get the whole Cm pattern.

We will now consider some subgroups of our plane group Cm.

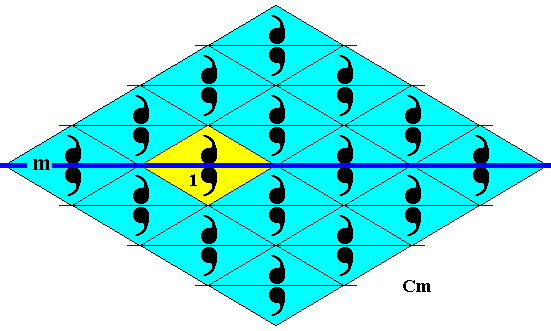
Figure 35. Subgroup (yellow) of the plane group Cm generated by reflection (of the identity element) in the line m . The symmetry of this subgroup is that of D₁ .

Figure 36. Subgroup (yellow) of the plane group Cm generated by the (implied) horizontal translation (of the identity element). The symmetry of this subgroup is that of the line group p11 . It is a frieze pattern. The (implied) horizontal an vertical translations of the parent group (full group) Cm are indicated at the bottom left (See also Figure 26 ).

Figure 37. Subgroup (yellow) of the plane group Cm generated by the implied horizontal translation and the generating horizontal reflection. It is a frieze pattern, and its symmetry is according to the line group p1m .

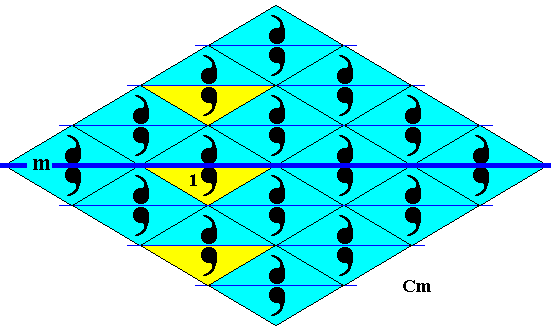
Figure 38. Subgroup (yellow) of the plane group Cm generated by the implied vertical translation. It is a frieze pattern, and its symmetry is according to the line group p11 .

Figure 39. Subgroup (yellow) of the plane group Cm generated by the implied horizontal and vertical translations. It is a plane pattern, and its symmetry is according to the plane group P1 (i.e. an asymmetric motif repeated by two independent translations). The identity of the (displayed) group elements is indicated, where t_v is the implied vertical translation, and t_h the implied horizontal translation, and where t_ht_h = t_h² , and t_h^-1 is t_h in the opposite direction (i.e. to the left).

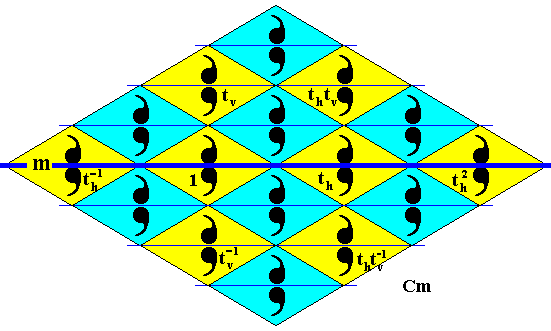
Figure 40. Subgroup (yellow) of the plane group Cm generated by the two implied translations (horizontal and vertical) and the generating mirror reflection in the horizontal line m . It is a plane pattern, and its symmetry is according to the plane group Pm .

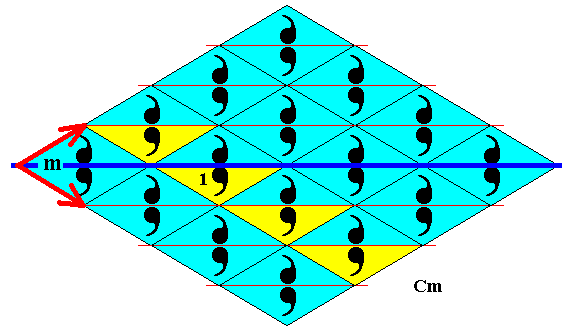
Figure 41. Subgroup (yellow) of the plane group Cm generated by the SE generating translation. It is a frieze pattern. Its symmetry is according to the line group p11 . The NE and SE (north-east and south-east) generating translations are indicated by red arrows.

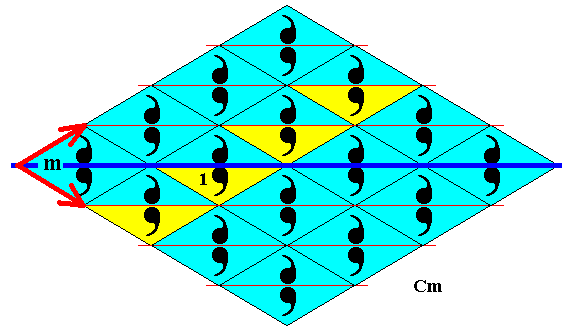
Figure 42. Subgroup (yellow) of the plane group Cm generated by the NE generating translation. It is a frieze pattern. Its symmetry is according to the line group p11 . The NE and SE generating translations are indicated by red arrows.

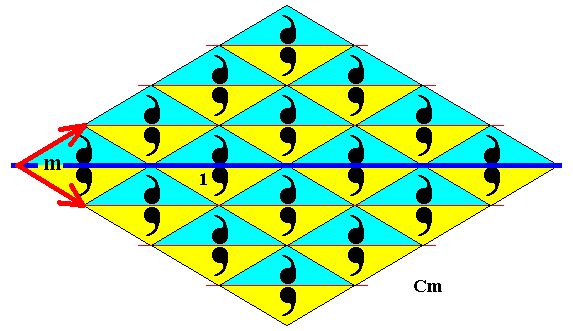
Figure 43. Subgroup (yellow) of the plane group Cm generated by the NE and SE generating translations. It is a plane pattern. Its symmetry is according to the plane group P1 . The NE and SE generating translations are indicated by red arrows.

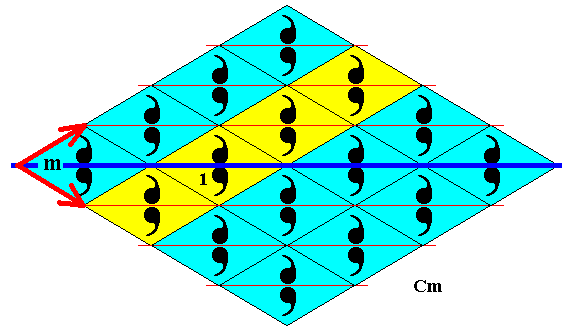
Figure 44. Subgroup (yellow) of the plane group Cm generated by the NE generating translation and the generating reflection in the horizontal line m . It is a frieze pattern. Its symmetry is according to the line group p11 . Although the motifs are mirror symmetric with respect to horizontal lines, these reflections are not symmetry transformations of the whole (sub)group, i.e. they are not elements of the group p11 . One can easily see that the frieze pattern (yellow)( which should be imagined to extend indefinitely in both directions) is not mirror symmetric in any one horizontal line. The NE and SE generating translations are indicated by red arrows.

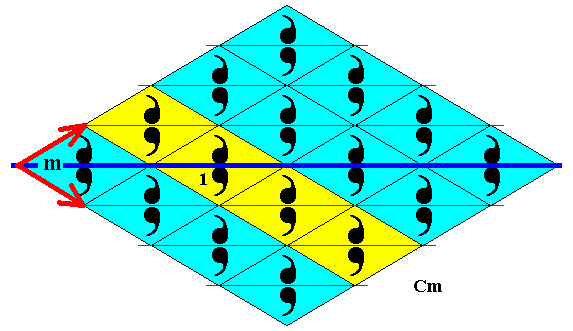
Figure 45. Subgroup (yellow) of the plane group Cm generated by the SE generating translation and the generating reflection in the horizontal line m . It is a frieze pattern. Its symmetry is according to the line group p11 . Again, although the motifs are mirror symmetric with respect to horizontal lines, these reflections are not symmetry transformations of the whole (sub)group, i.e. they are not elements of the group p11 . The NE and SE generating translations are indicated by red arrows.

In the next document we will give an example of an antisymmetry ornament derived from a Cm pattern in Neolithic art, and continue our study of antisymmetry, subpatterns and subgroups in ornaments, where we will begin with the plane group C2mm.

e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology).

back to homepage

Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology

Back to subpatterns and subgroups (introduction)

Back to subpatterns and subgroups Part II

Back to subpatterns and subgroups Part III

Back to subpatterns and subgroups Part IV

Back to subpatterns and subgroups Part V

Back to subpatterns and subgroups Part VI

Back to subpatterns and subgroups Part VII

Back to subpatterns and subgroups Part VIII

Back to subpatterns and subgroups Part IX

Back to subpatterns and subgroups Part X