
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite two-dimensional periodic patterns, or Ornaments (sequel)
We will now illustrate all the 17 plane group patterns with their motifs. s.str. as seen (i.e. as interpreted) with their centra located inside the lattice meshes (With respect to the plane group P1 we have always done so, but in order to be complete we give it anyway). Also choices of fundamental regions are shown. Such a fundamental region tesselates the plane and contains an asymmetric figure as its motif s.str. Therefore each such region can represent a group element [ This is shown in more detail on the Third Part of the website, accessible by a HOLISTIC Philosophy as an alternative world view , and then see there at Crystals and the Implicate Order (Part I -- XIX)].
The first Figure illustrates the plane group P1 .

Figure 1. Pattern representing plane group P1 . The motifs s.str. are (chosen to be) commas, placed inside the lattice meshes. Such a lattice mesh can at the same time represent a fundamental region (containing an asymmetric motif s.str. ).
When it comes to the plane group P2 we note that we see -- with respect to symmetry -- the same motif s.str., whether we see it from a lattice point (i.e. with its center coinciding with a lattice point) or whether we see it from the mid-point of a lattice mesh. In both cases we see a motif s.str. with the symmetry of the group C2 , consisting of two commas related to each other by a half-turn. See next Figure.

Figure 1a. Pattern representing te plane group P2 . A motif s.str. with C2 symmetry can be seen at each lattice point as well as at the center of each lattice mesh.
The next Figure illustrates the plane group P2 with the motifs s.str. viewed as having their center located at the middle of a lattice mesh.

Figure 2. Pattern representing plane group P2 . The motifs s.str. are (chosen to be) dual-commas, placed inside the lattice meshes (as the circle indicates). Half a lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit of the motif s.str. . A lattice mesh is indicated (blue).
The next Figure gives another choice of the fundamental region of the same pattern.

Figure 3. Alternative choice of fundamental region of the pattern of the previous Figure. Also here each such region contains an asymmetric figure as its motif s.str.
A lattice mesh is indicated (blue).
Let's now consider the plane group Pm . Normally we viewed the motifs s.str. as having their centers coinciding with the lattice nodes, as the next Figure shows.
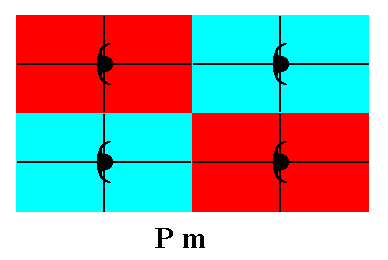
Figure 4. Unit mesh and motifs of a Pm pattern. The motif s.str. is considered to have its center coincide with a lattice point. So in this interpretation we have four motifs s.str. , each one having its center at a different lattice node. The symmetry of such a motif is D1 .
Alternatively, however, we can view the same configuration, as depicted in the above Figure, differently. The parts of the motifs s.str. that belong to the mesh of the lattice (i.e. are inside that mesh) together can be seen as one motif s.str. having its center in the middle of the mesh. See next Figure.
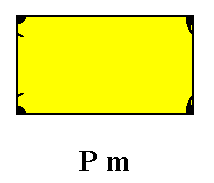
Figure 5. Unit mesh of the same pattern as in the previous Figure. The motif s.str. is now seen as having its center in the middle of the mesh. The symmetry of this motif, so conceived, is again that of D1 .
Because the motif s.str. as seen in the above Figure has the same symmetry as it had when conceived as a motif having its center coincide with a lattice point (Figure 4), we can simply replace the motif as it is in Figure 5, by any D1 motif placed in the middle of the mesh (i.e. with its center coinciding with the mid-point of the mesh). See next Figure.

Figure 6. Motif s.str. chosen to figure in a pm pattern.
The next Figure illustrates the plane group Pm with the motifs s.str. as they are conceived in the previous Figure.
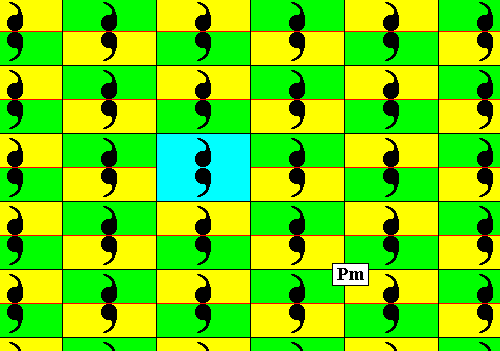
Figure 7. Pattern representing plane group Pm . The motifs s.str. are (chosen to be) dual-commas, placed inside the lattice meshes. Half a lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit of the motif s.str. . A lattice mesh is indicated (blue).
The next Figure illustrates the plane group Pg along the same lines.

Figure 8. Pattern representing plane group Pg . The motifs s.str. are (chosen to be) dual-commas, placed inside the lattice meshes. Half a lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit of the motif s.str. . A lattice mesh is indicated (blue).
The next Figure gives this same Pg pattern, but with another choice of fundamental region.

Figure 9. Another choice of fundamental region for the pattern of the previous Figure. (Generally several choices of unit mesh are possible. Here two are shown).
As in the case of the group Pm we see that in the group P2mm the symmetry at a lattice point is the same as at the mid-point of a lattice mesh (both D2 symmetry) :
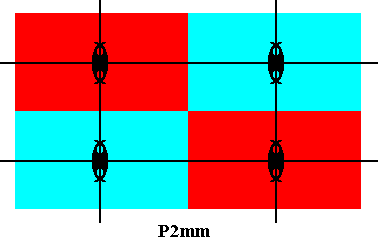
Figure 10. Lattice mesh of a P2mm pattern. A motif s.str. has the same symmetry, whether it is viewed as having its center at a lattice node, or whether it is viewed as having its center at the middle of a lattice mesh.
So in virtue of the above, we can, in building a P2mm pattern, simply place a motif with symmetry D2 in the center of each lattice mesh, as the next Figure shows.

Figure 11. Pattern representing plane group P2mm . The motifs s.str. are (chosen to be) a set of four commas, and as such placed inside the lattice meshes. A quarter of a lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit (comma) of the motif s.str. . A lattice mesh is indicated (blue).
In the plane group P2mg we see that the symmetry at a lattice node is the same as at the center of a mesh. See next Figure.
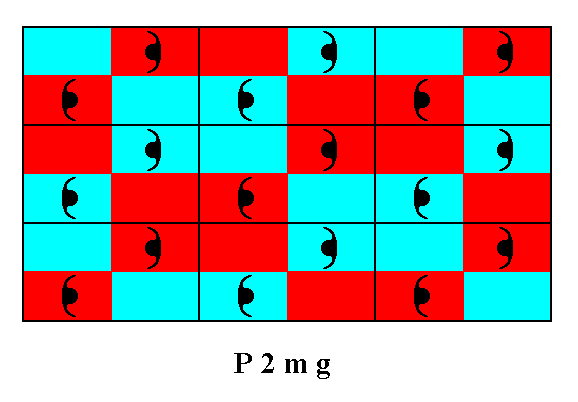
Figure 12. Pattern representing the plane group P2mg . The symmetry at a lattice point is the same as at the center of a mesh.
Because of what we see in the above Figure, we can simply place in the center of each lattice mesh a motif s.str. consisting of two units, each having D1 symmetry, that are related to each other by a glide reflection along a vertical line. And so, in fact, can the above Figure (also) be interpreted. The next Figure shows this yet again (for smaller meshes).
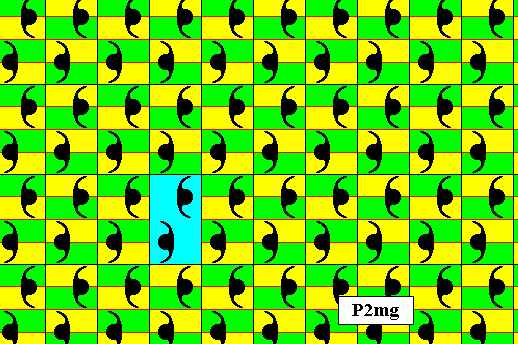
Figure 13. Pattern representing plane group P2mg . The motifs s.str. are (chosen to be) a set of four commas (two by two partly overlapping), and as such placed inside the lattice meshes. A quarter of a lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit of the motif s.str. . A lattice mesh is indicated (blue).
The next plane group we will consider in this respect is the group P2gg .
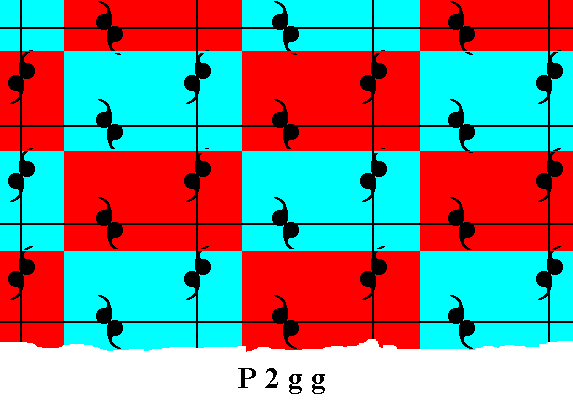
Figure 14. Pattern representing the plane group P2gg .
If we isolate a lattice mesh, we can see what motif s.str. is inside it. In this we consider the mid-point of the mesh as the center of this motif s.str. See next Figure.
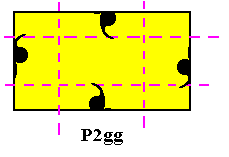
Figure 15. Motif s.str. of the P2gg pattern of Figure 14. Glide lines are indicated by dashed lines.
In the above Figure we can see that the motif s.str. consists of four units that are related to each other by the glide lines indicated. So we now know that we can simply replace this motif by another, in such a way that the replacing motif consists of four asymmetric units close together and related to each other by two plus two glide lines perpendicular to each other. See next Figure.

Figure 16. Pattern representing plane group P2gg . The motifs s.str. are (chosen to be) a set of four commas, and as such placed inside the lattice meshes. The commas in a mesh are related to each other by four glide lines. A quarter of a lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit (comma) of the motif s.str. . A lattice mesh is indicated (blue).
The next Figure shows the glide lines of our P2gg pattern.
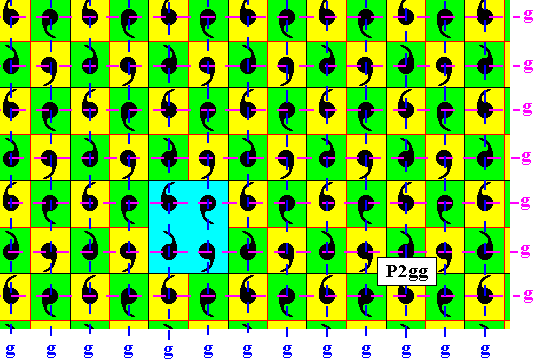
Figure 17. The P2gg pattern of the previous Figure, with its glide lines indicated (dashed lines).
In the next document we will continue our investigation of the plane group patterns with respect to the interpretation of the center of the motif s.str.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology)
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV
Back to subpatterns and subgroups Part V
Back to subpatterns and subgroups Part VI
Back to subpatterns and subgroups Part VII