e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite two-dimensional periodic patterns, or Ornaments
Introduction
Here, and in the next three documents, we'll prepare to discuss antisymmetry groups, some subgroups, and one or more colored symmetry groups, derivable from the 17 infinite two-dimensional patterns. The reason that we call them two-dimensional is the fact that the (2-dimensional) motifs are repeated along two independent translation directions (instead of only one such direction as is the case in friezes). Because of these two translation directions there are no invariant subspaces in such patterns (points are shifted, but also lines are shifted). As in friezes, their symmetries are isometries. So their common BOHM symbol is G2 (Isometries, two-dimensional motifs, no invariant subspaces), the symmetry groups of Ornaments (i.e. ornaments s.str.). There are exactly 17 discrete symmetry types of ornaments, described by seventeen Plane Groups. With "discrete" we mean that there is no symmetry transformation that involves a displacement (of a point) that is infinitely small (as can be the case in continuous ornaments).
The discrete ornaments have already figured a number of times on this website. We can refer the reader to the following places where they were introduced and described (geared to certain different objectives) :
Alternative centers of the motifs s.str. in the 17 Plane Group patterns (ornaments).
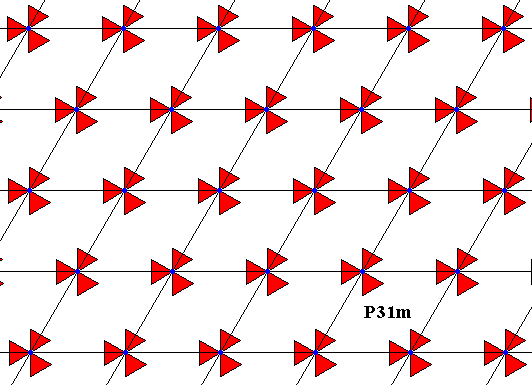
A periodic two-dimensional pattern (ornament, G2 ) consists of motifs s.str. and corresponding background. But such a motif can be differently conceived depending upon which point is considered to be the center of such a motif. We can explain this by considering an ornament according to the Plane Group P31m . See next Figure.

Figure 1. Pattern according to the plane group P31m . The two-dimensional point lattice is indicated : blue dots with black connection lines. Each motif s.str. is a dihedral figure, having the structure of the group D3 , provided its center is represented by a lattice node.
The next Figure illustrates the motifs s.str. as having their centers coincide with lattice nodes.
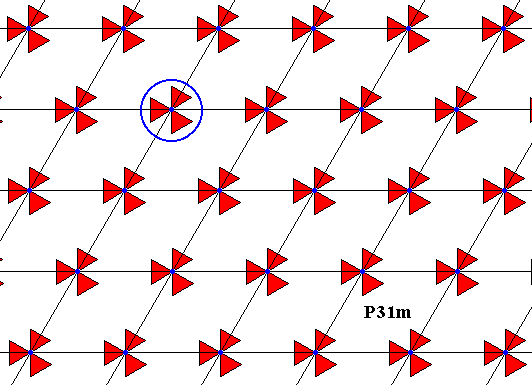
Figure 2. Motif s.str. considered as having its center coinciding with a latice node. As such it has D3 symmetry.
But in the same pattern we can conceive the motifs s.str. otherwise, namely as having their centers coinciding with the center of a triangle (which is half a rhombic unit mesh) :
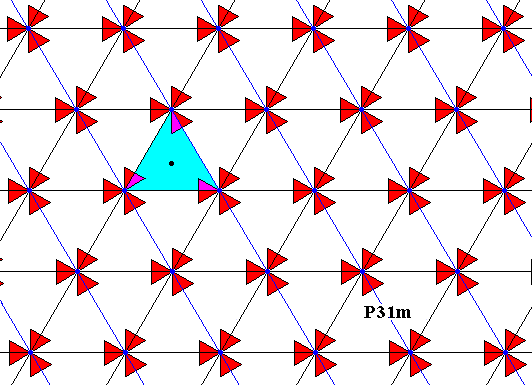
Figure 3. The same pattern as above, but now with the motif s.str. considered as having its center in the middle of a triangle (which makes up half a rhombic unit mesh). As such this motif now has C3 symmetry (instead of D3 symmetry).
The next Figure isolates this motif in order to show its C3 symmetry.
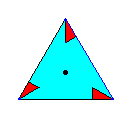
Figure 4. Isolated motif s.str. of the pattern of the previous Figure. This motif clearly has C3 symmetry.
When we now consider a pattern according to the plane group P3m1 we see that also there the motifs s.str. have the structure of D3 if we conceive them as having their centra coinciding with lattice nodes, and if we consider them as having their centra coincide with the mid-points of the triangles (each of which is half a rhombic unit mesh), then such motifs, so conceived, still possess the structure of D3 . See next Figure.
Figure 5. Pattern representing the plane group P3m1 .
The motif s.str. , whether conceived as having its center coinciding with a lattice point, or as having its center coinciding with the middle of a triangle (which is half a rhombic unit mesh) has D3 symmetry. This is especially evident when considering the upper triangle (blue) of the lattice mesh (unit mesh). Like the periodic patterns above, this pattern must be imagined to be extended indefinitely over the plane.
With all this we have found an easy and convenient visual way to discriminate between the groups P31m and P3m1 . We can do this by placing appropriate motifs s.str. not at the lattice points, but at the centers of the triangles of the hexagonal point lattice. See next Figures.
Figure 6. Pattern according to the plane group P31m .
Each rhombic mesh of the hexagonal point lattice contains two motifs with rotational symmetry C3 . These two motifs are mirror symmetric with respect to each other, i.e. they are reflections of each other in the shorter diagonal of the rhombic mesh. Indeed it is this reflection line which demands an enantiomorphic counterpart of the motif s.str. to be present. So if we replace the existing motifs-s.str.-at-the-lattice-points by motifs-s.str.-inside-the-rhombic-mesh, then both triangles of a rhombic mesh must be supplied with such a motif, in such a way that each rhombic mesh contains both enantiomorphic forms of the motif, i.e. a right-handed and a left-handed version of it, which are mirror symmetric images of each other.
The next Figure shows that the motif s.str. conceived as having its center coinciding with a lattice node has D3 symmetry.
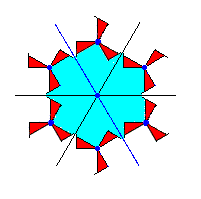
Figure 7. Motif s.str. of the P31m pattern of the previous Figure, conceived as having its center at a lattice point. It has D3 structure.
In the same way we can obtain the alternative pattern, now with respect to the group P3m1 , i.e. a pattern obtained by replacing the existing motifs-s.str.-at-the-lattice-points by appropriate motifs inside the rhombic lattice meshes. Placing one such motif in each of the two triangles of the rhombic mesh, yields the following P3m1 pattern :
Figure 8. Pattern representing the plane group P3m1 . Each rhombic unit mesh of the hexagonal lattice contains two motifs s.str. each with D3 symmetry.
So the Figures 6 and 8 clearly show the difference between the plane groups P31m and P3m1 .
The next Figure shows that the pattern, as obtained in Figure 8 has no 6-fold rotation axes (as might seem so at first sight).
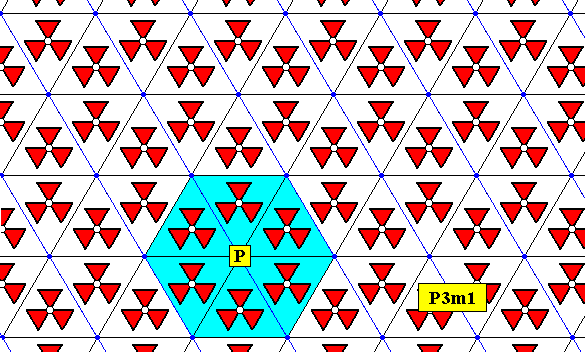
Figure 8.1. The point P (and consequently all lattice points) is not the seat of a 6-fold rotation axis : The six 3-fold motifs all have the same orientation. So they can only be images of a rotation of 00, 1200 or 2400, and so not of 600.
Because the motifs of the P3m1 pattern (as in Figure 8) have themselves indirect symmetries (namely reflections) -- they have D3 structure -- there do not exist enantiomorphic forms of them, which means that the presence of mirror symmetries as group elements in the group P3m1 do not demand both enantiomorphic counterparts to be present, because there aren't such counterparts (Of a D3 structure, like an equilateral triangle, we cannot have a left-hand version and a right-hand version which are different from each other). Because of this, it is so that if we -- when carrying out the mentioned replacements of motifs s.str. -- supply only one of the triangles of the rhombic meshes with a D3 motif, the D3 symmetry of the other triangle is automatically implied. See next three Figures.
Figure 8a. Pattern representing the plane group P3m1 , obtained by replacing the motifs-s.str.-at-the-lattice-points by one motif-s.str.-inside-the-lattice-mesh, i.e. filling in one of the two triangles of the rhombic meshes with a motif s.str.
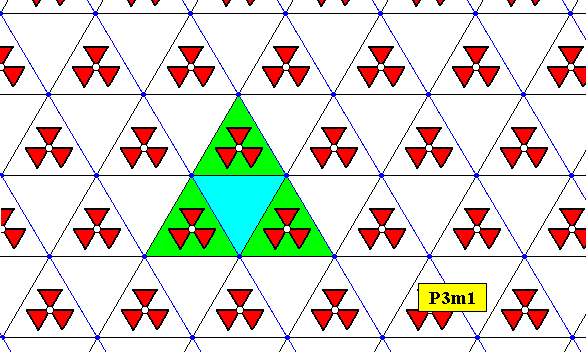
Figure 8aa. The empty triangle (and its surroundings) in the pattern of the previous Figure automatically represents D3 symmetry : There are three mirror lines that intersect in the center of the triangle and which center represents a 3-fold rotation axis.
The next Figure shows that the pattern so obtained is indeed identical to the original pattern.
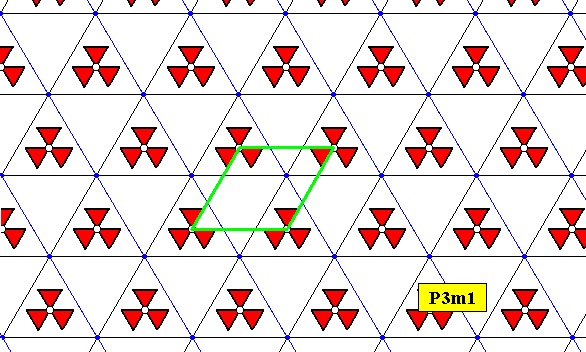
Figure 8b. The obtained P3m1 pattern is the same as the original pattern of Figure 5.
The next Figures consider the fundamental region of the two patterns.
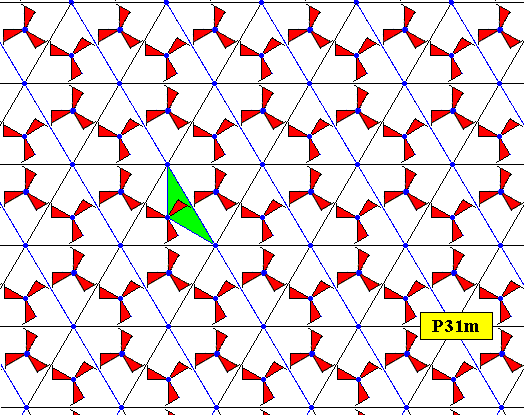
Figure 9. Fundamental region (green) of the P31m pattern of Figure 6.
The next Figure shows the orbit of this fundamental region, resulting in copies that tesselate the plane completely.

Figure 10. Tiling of the plane by the fundamental region and its copies of the P31m pattern of the previous Figure. The colors only serve to indicate all these fundamental regions. Each fundamental region contains exactly one asymmetric unit of the motif s.str. , therefore each such region can represent a group element.
In order to let come out the structure of our P31m pattern clearly (and to compare it with a pattern representing plane group P3m1 ), we emphasize the triangular nature of the pattern :
Figure 10a. Triangular aspect of the P31m .
The fundamental region of the pattern representing plane group P3m1 , as depicted in Figure 8, is (necessary) of the form of an equiangular triangle, the sides of which are mirror lines of the pattern. The next Figure depicts this region.
Figure 11. Fundamental region (green) of the P3m1 pattern of Figure 8.
The next Figure isolates this fundamental region in order to show that it (as was also the case in the P31m pattern) contains an asymmetric figure, which is part of (in this case two) motif s.str.

Figure 12. Fundamental region of the P3m1 pattern of the previous Figure. It contains an asymmetric motif.
The next figure shows that the orbit of this fundamental region tesselates the plane completely.

Figure 13. Tesselation (tiling) of the plane by the fundamental region of the P3m1 pattern of Figure 11. Each fundamental region contains an asymmetric figure. Therefore they can represent group elements.
When we use only two colors to indicate the fundamental region and its copies, we get the following :
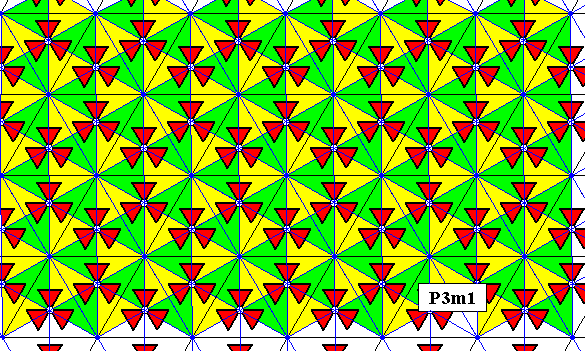
Figure 14. The same as previous Figure, but now only two colors used to designate the fundamental region and its copies (resulting from its orbit).
The next Figure shows the triangular nature of also the P3m1 pattern :
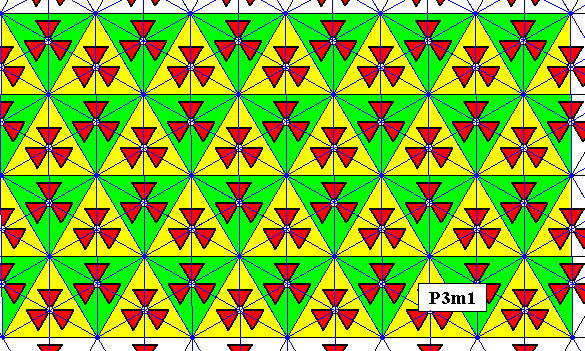
Figure 15. Triangular nature of the P3m1 pattern. Compare with Figure 10a.
The difference between the two plane groups now clearly stands out :
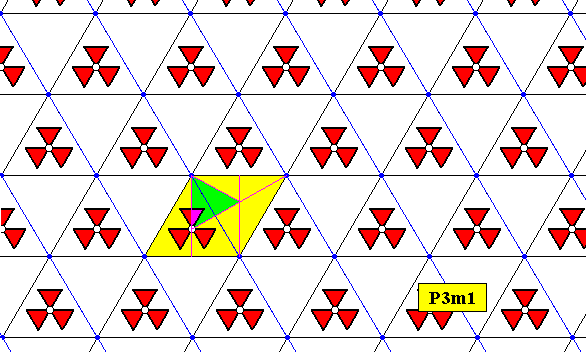
Figure 16. Fundamental region (green) of the P3m1 pattern as (this version of the pattern) was obtained earlier (Figure 8a) by replacing the motifs-s.str.-at-the-lattice-points by one motif-s.str.-inside-the-rhombic-meshes. The fundamental region contains one asymmetric unit of the motif s.str. Compare with Figure 11.
We will now draw the tesselation that results from the orbit of this fundamental region, i.e. we will draw all its copies, which as such represent group elements.
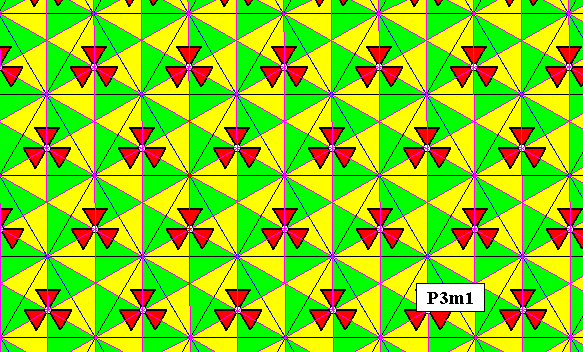
Figure 17. Fundamental region and its copies (yellow and green) of the P3m1 pattern of Figure 16. Each such region contains one asymmetric unit of the motif s.str. . Therefore it can represent a group element.
The next Figure shows this same pattern, but now with the rhombic lattice mesh indicated.
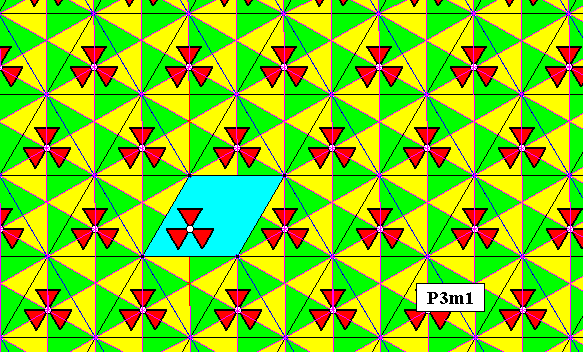
Figure 18. The P3m1 pattern of Figure 17, with rhombic lattice mesh emphasized (blue).
While in the present document having said something about the difference between the two above mentioned plane groups, which came out clearly when viewing the motifs s.str. as having their centers inside the rhombic unit mesh of the hexagonal two-dimensional point lattice (instead of viewing those same motifs as having their centers coinciding with the lattice points), in the next document we will do so for all the 17 plane groups, and indicate (a choice of) the fundamental region, which, together with its copies, can represent group elements. Further we will use for the plane groups Cm and C2mm a rhombic lattice, instead of a centered rectangular lattice (both lattices are, however, equivalent).
All this is done with the sole purpose of clarifying still further the plane group patterns (ornaments s.str.). When we later are going to discuss the antisymmetry groups (and some examples of colored symmetry groups) derived from those patterns, we can choose between the two methods for viewing (i.e. for interpreting) the motifs s.str. with respect to their centers.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology)
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV
Back to subpatterns and subgroups Part V
Back to subpatterns and subgroups Part VI