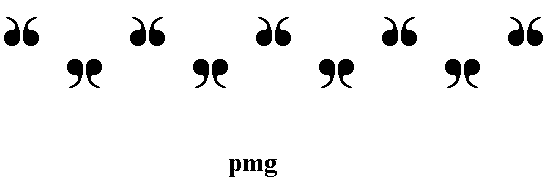
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite one-dimensional periodic patterns, or friezes (sequel)
We continue our study of friezes (line groups) with the group pmg .
Presentation and structure :
pmg
{g, m} m2 = (mg)2 = 1 or,
{m, h} m2 = h2 = 1 (h = mg)
Structure Dinfinite .
Where m is a reflection in a line perpendicular to the frieze axis, g a glide reflection along the frieze axis, and h is a half-turn (about a certain point).
The line group pmg can be realized as (or represented by) the following frieze pattern (We have discussed this group earlier, in Part II, in connection with expounding the theories of antisymmetry and colored symmetry) :
Figure 1. A possible realization of the group pmg .
The pattern must be imagined to extend indefinitely to the right as well as to the left.
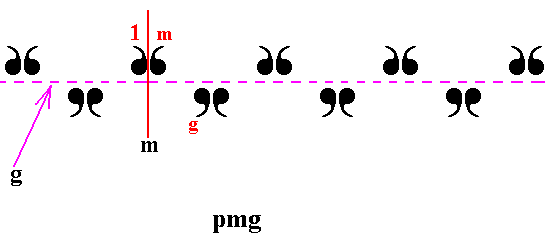
Figure 2. The group pmg can be generated by a glide reflection g parallel to the frieze axis and a reflection m in a reflection line perpendicular to the frieze axis.
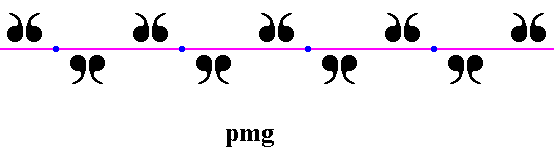
Figure 3. The repetition of motifs is described by a one-dimensional point lattice (indicated by blue dots and connection lines). Each lattice node (lattice point) is associated with an equivalent area of the pattern (i.e. the surroundings of each node are identical). As such each lattice node is associated with four units (commas) of a motif s.str. , itself consisting of four motif units, commas). Each such motif unit (comma) can represent a group element.
On the basis of the point lattice determined above, we can depict the motifs s.l. of our pmg pattern. See next Figure.

Figure 4. Motifs s.l. (blue and red strips) of the pmg pattern under consideration. Each motif s.l. is associated with a lattice node and consists of one motif s.str. (itself consisting of four asymmetric units (commas)) PLUS corresponding back ground. Each motif s.l. extends indefinitely upwards and downwards. The red and blue colors do not signify any asymmetry, but only serve to highlight the motifs s.l. The dark blue dots represent lattice points. The figure illustrates the fact that the frieze is carried by the two-dimensional plane (E2).
When we now partition these motifs s.l. properly, we obtain maximal areas (a fundamental region and its copies) that represent group elements :

Figure 5. Partition of the motifs s.l. such that the resulting areas (red, blue) represent group elements. Each such area contains one (asymmetric) unit (comma) of the motif s.str. and extends indefinitely upwards and downwards. The dark blue dots represent lattice points. The colors red and blue do not -- in the present context -- signify any asymmetry, but only serve to highlight the group elements.
The next Figure adds some markings to some areas in order to point to the identity element 1 and the generators g (glide reflection parallel to the frieze axis) and m (mirror reflection in the line m perpendicular to the frieze axis).
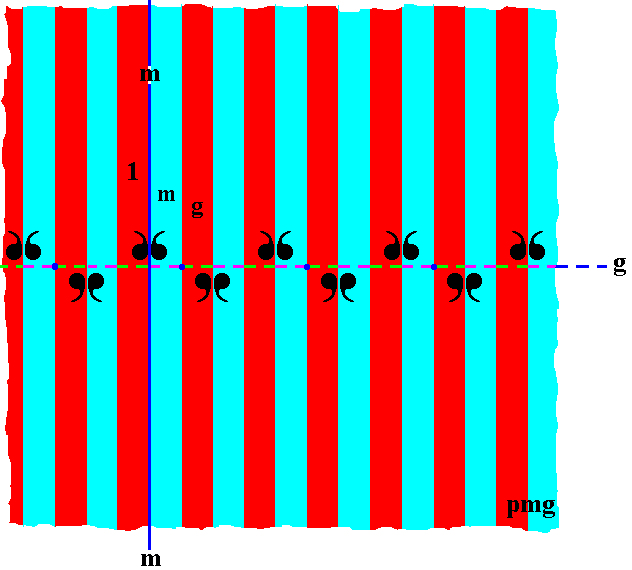
Figure 6. Indication of the identity element, and of the two (possible) generators of the group pmg . The mirror line m (solid vertical line) and the glide line g (dashed horizontal line) are indicated.
In the next Figure the rest of the areas (of the displayed part of the pattern) have been filled in with the proper symbols of the group elements (or we can say, we have generated the group from the initial element -- identity element -- by repeatedly applying the two generators g and m ).
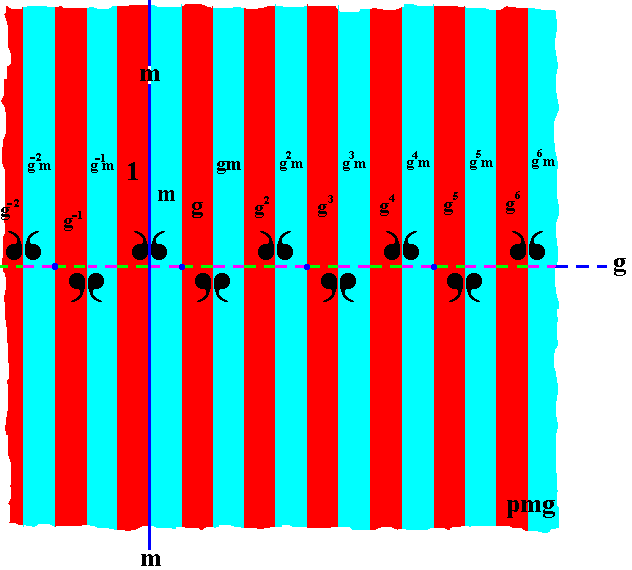
Figure 7. Generation of the group pmg .
Each vertical area of the displayed part of the pattern is provided with a mark that tells what group element is being represented by that area. The colors red and blue of the areas do not -- in the present case -- signify any asymmetry, they only serve to highlight the group elements.
In the above Figures the symmetries and asymmetries were indicated by the positions, mutual relations and orientations of the units (commas) of the motifs s.str. The colors of the areas were not supposed to express these symmetries, but only to highlight the fundamental region and its copies.
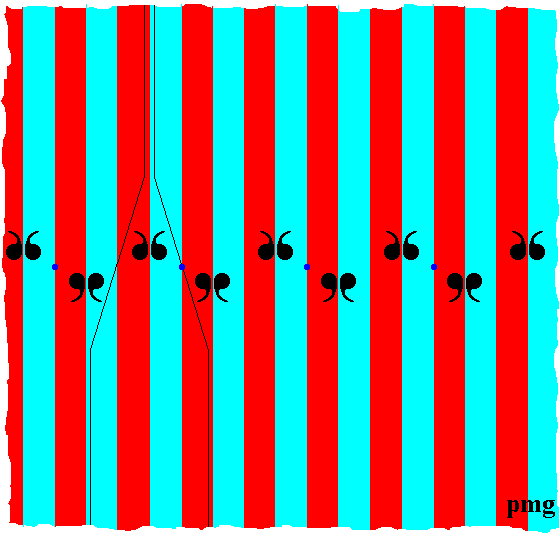
Figure 8. First phase of construction of new fundamental areas accounting for all symmetries of the pmg pattern. The colors do not signify symmetries or asymmetries of the pattern.

Figure 9. Construction of the new fundamental region and its copies (red, blue). As before, each such region (area) contains one unit (comma) of the motif s.str. , and the colors do not signify symmetry features, but only highlight the new fundamental region and its copies. We can clearly see that the shape, position and mutual relation of these new areas (representing group elements) express the glide reflections, mirror reflections and the (implied) 2-fold rotation axes. Each area extends indefinitely upwards as well as downwards, and the pattern extends indefinitely to the right as well as to the left. The lattice nodes are indicated by dark blue dots.
Because the function of the units (commas) of the motifs s.str. has been taken over by the shape, position and mutual relation of the fundamental region and its copies, we can erase the commas :
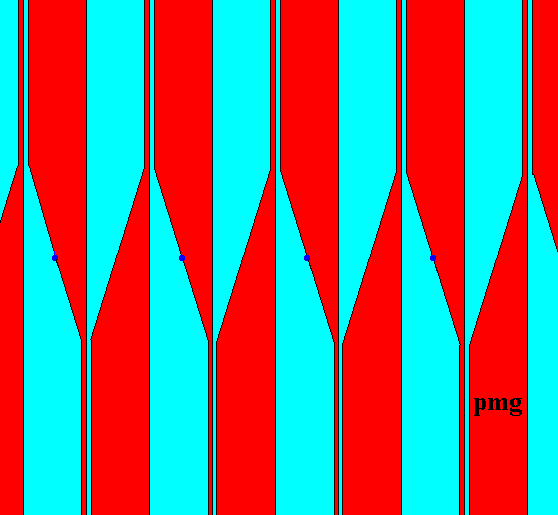
Figure 10. Erasion of the commas. The pattern of fundamental regions now expresses all the symmetries of the group pmg . The dark blue dots represent lattice nodes.
The next Figure shows the group elements explicitly in this commaless pattern.
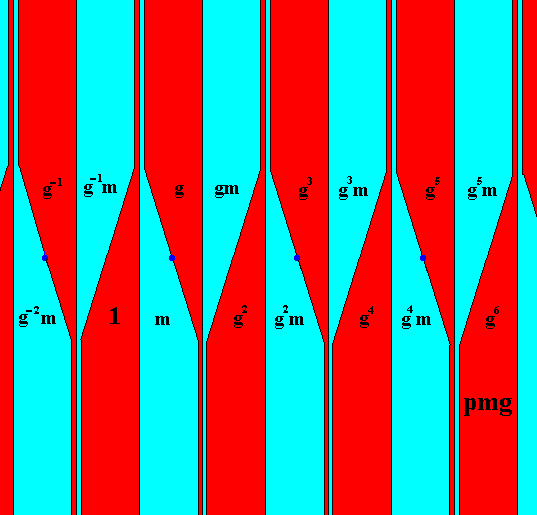
Figure 11. Identification of the group elements, each represented by a fundamental area or one of its copies (red, blue). The colors red and blue do not signify symmetry features of the pmg pattern, only the geometry does so.
Presentation and structure :
p1m
{t, m} m2 = 1 mt = tm
Structure Cinfinite x D1 .
Where t is a translation along the frieze axis, and m is a reflection in the frieze axis.
The next Figure shows a possible realization of the line group p1m .
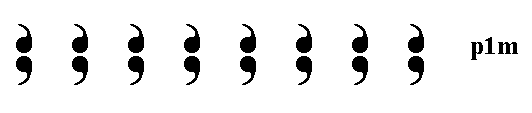
Figure 12. A frieze pattern representing the line group p1m .
The next Figure indicates the underlying one-dimensional point lattice, that describes the repetition of pattern units.
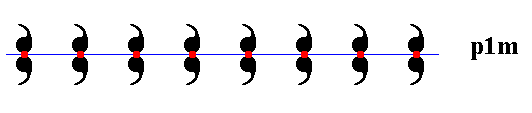
Figure 13. Frieze pattern according to the line group p1m with the one-dimensional lattice indicated. The lattice points (lattice nodes) are shown by red dots. Each lattice node is associated with a motif s.str. which consists of two symmetrically related units (commas). The lattice nodes indicate equivalent areas of the pattern.
We're now going to determine the motifs s.l. of our p1m pattern. See next Figures.

Figure 14. Motifs s.l. (red, blue) of the p1m pattern depicted above. Each motif s.l. extends across the lattice connection line, and so is a vertical strip, upwards and downwards unbounded, and consisting of one motif s.str. , itself consisting of two symmetrically related units (commas), PLUS corresponding background. The red and blue colors do not signify any asymmetry, but only serves to highlight the motifs s.l. The lattice nodes are indicated by yellow dots, and are each associated with one motif s.l.
In the present case it is possible to express the symmetry of the motif s.str. (and also the asymmetry of its units (commas)) fully by the shape, orientation and mutual relationship of plane-tesselating areas representing the motifs s.l . See next Figure.

Figure 15. Motifs s.l. (blue, red) of the p1m pattern. These motifs s.l. fully express with their geometry (i.e. the shape and orientation of the areas representing these motifs) the symmetry of the motifs s.str. Each motif s.l. is a chevron-shaped area, containing one motif s.str. itself consisting of two symmetrically related units (commas). The red and blue colors do not signify any asymmetry.
These motifs s.l. must be partitioned in such a way that each resulting area represents a group element, and is associated with one (asymmetric) unit (comma) of the motif s.str. . See next Figure.

Figure 16. Partitioning of each chevron-shaped motif s.l. into its symmetrical halves, resulting in plane-tesselating areas that can represent group elements. Each such area is an oblique strip, containing one unit (comma) of the motif s.str. itself consisting of two such units. The red and blue colors do not signify any asymmetry.
The next Figure shows one of these areas to represent the identity element 1 and two others to be the generators t (translation along the frieze axis) and m (reflection in the frieze axis).

Figure 17. Areas (red, blue) representing group elements. Some of these are marked as being the identity element 1 and the two generators t (translation) and m (reflection).
We can now fill in the remaining elements :
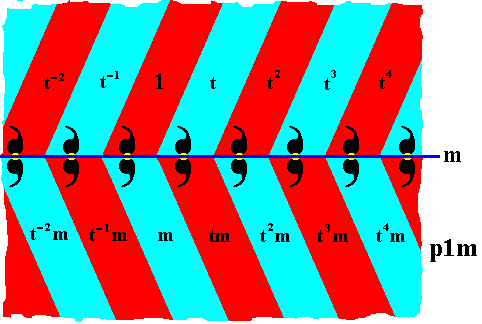
Figure 18. Areas representing group elements of the group p1m , marked with the identity of the group elements.
Because the function of the units (commas) of the motifs s.str. is fully taken over by the shape, orientation and mutual relationship of the areas representing group elements, we can dispose of those commas. See next Figure.
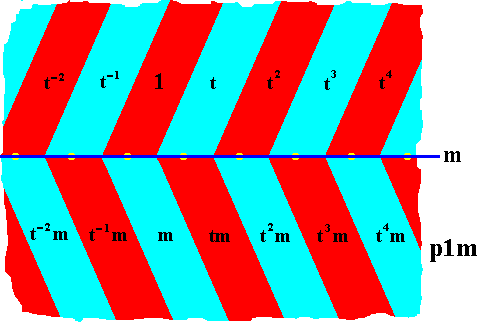
Figure 19. Tesselation of the plane by areas representing group elements of the line group p1m . These areas geometrically fully represent the asymmetry of the comma. The latter is therefore erased.
Presentation and structure :
pmm
{t, m, m1} m2 = m12 = (m1t)2 = 1 mt = tm mm1 = m1m or,
{m, m1, m2} m2 = m12 = m22 = 1 mm1 = m1m mm2 = m2m (m2 = m1t)
Structure Dinfinite x D1 .
Where t is a translation along the frieze axis, m a reflection in the frieze axis, and m1 and m2 are reflections in lines perpendicular to the frieze axis.
The next Figure gives a possible realization of the line group pmm .
Figure 20. A periodic pattern according to the line group pmm .
The repetition of motifs of this pattern is based on a one-dimensional point lattice, as the next Figure shows.

Figure 21. One-dimensional point lattice describing the repetition of motifs of the pmm pattern. Each lattice node (red dot) is associated with a motif s.str. itself consisting of four units (commas). These four units are arranged according to the (sub)group D2 . Each lattice node is associated with an equivalent area of the pattern.
On the basis of the one-dimensional point lattice we can determine the motifs s.l. of our pmm pattern :

Figure 22. Motifs s.l. (red, blue) of the pmm pattern. Each motif s.l. extends across the lattice connection line, and is therefore a vertical strip. Each motif s.l. consists of one motif s.str. (itself consisting of four units (commas)) PLUS corresponding background, and is associated with a lattice point (indicated by a yellow dot). Upwards and downwards such a motif is unbounded. The colors red and blue do not signify any asymmetry, they only serve to highlight the motifs s.l.
The next Figure shows a partition of the motifs s.l. into tesselating areas in such a way that these resulting areas represent group elements of the group pmm .

Figure 23. Areas (blue, red) representing group elements of the line group pmm . Each such area is unbounded either downwards or upwards, and contains one unit (comma) of the motif s.str. The lattice nodes are indicated by yellow dots. The colors red and blue do not signify any asymmetry, but only serve to highlight the areas representing group elements.
We will now indicate one such area as being the identity element 1 and three others as the generators t (translation along the frieze axis), m (reflection in the frieze axis) and m1 (reflection in a line m1 perpendicular to the frieze axis). See next Figure.
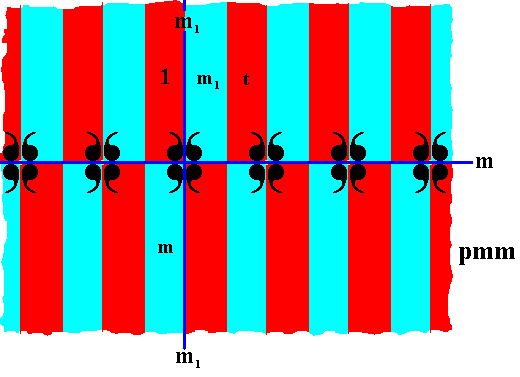
Figure 24. The pmm pattern.
Indication of the identity element 1 and the generators t (translation), m (reflection in the frieze axis) and m1 (reflection in the line m1 perpendicular to the frieze axis).
The red and blue colors do not signify any asymmetry, but only serve to higlight the areas representing group elements.
Now we can fill in the rest of the group elements of the displayed part of the pattern :
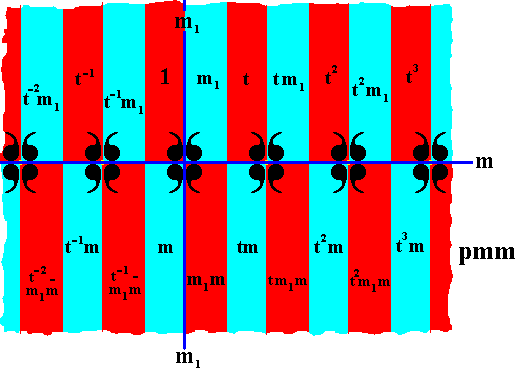
Figure 25. Marking the areas representing group elements in terms of the generators t, m, m1 . The red and blue colors do not signify any asymmetry, but only serve to higlight the areas representing group elements.
Friezes are patterns that repeat along one line, i.e. in one direction (and its opposite counterpart) only. They (in principle) indefinitely extend in the directions opposite to the repeat axis (frieze axis), but do not indefinitely repeat in those directions. In this sense they are one-dimensional periodic patterns.

Figure 26. An inserted comma destroys the pmm-symmetry of the depicted frieze completely and turns it into a rosette, the symmetry group of which is isomorphic to the group C1.
If two mirror-symmetrically related commas are inserted in such a way that their reflection line coincides with one or another reflection line of the frieze pattern, then the frieze will turn into a rosette with symmetry group D1 (which is isomorphic to C2 ). See next Figure.

Figure 27. Insertion of two commas, that are mirror images of each other, into an initial frieze pattern in such a way that the mirror line relating the two commas coincides with a mirror line of the frieze pattern, results in a pattern that has as its only symmetry element a mirror line, implying that its set of symmetry transformations consists of the identity and a reflection transformation only, and so forms a group of D1 structure (despite the fact that the pattern is still infinite). The two inserted commas cause a cessation of periodicity in whatever direction, and that's why the frieze changes into a rosette.
If we insert two structural units symmetrically related to each other by a half-turn, in such a way that the center of the halt-turn coincides with one or another 2-fold rotation center of the frieze pattern, the frieze will become a rosette with symmetry group C2 (which is isomorphic to D1 ), because then the only symmetry element is one 2-fold rotation axis (resulting in two group elements, the identity and a half-turn). See next Figure.

Figure 28. Insertion of one 2-fold motif (two black rectangles) into a frieze pattern, in such a way that the rotation axis of this motif coincides with a 2-fold rotation axis of the frieze pattern, results in a rosette with symmetry group C2 . The coinciding 2-fold rotation axes are indicated by a red dot.
And if the (frieze) pattern becomes finite in the repeat direction, it also turns into a rosette. See next Figure.
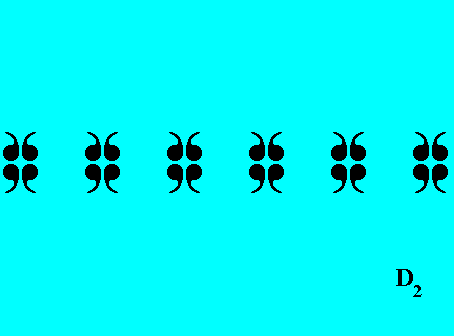
Figure 29. When a frieze pattern becomes finite at least in the direction of the frieze axis (which is the direction of repetition of units), it changes into a rosette. In the present case we have obtained a rosette with symmetry group D2 (It has two mirror lines perpendicular to each other, and a 2-fold rotation axis going through their intersection point, while it is perpendicular to the plane determined by those two mirror lines).
When a 'frieze' is finite in the direction of the frieze axis, but in such a way that the (finite) number of repetitions is still quite large, we can describe it as a pattern with approximate frieze symmetry. For patterns with two independent directions of repetitions this is mutatis mutandis the case in crystals. There the number of repetitions is very large indeed, in fact so large that this number can savely be considered to be infinite. That's why crystal structure is described by plane groups, which are the two-dimensional counterparts of friezes. But in fact the structure of crystals displays approximate plane group symmetry.
This concludes our general treatment of the seven friezes G21 (which can figure as subgroups of ornaments G2 ).
The next document will consider antisymmetry groups that can be derived from the friezes, and subgroups not related to antisymmetry (or colored symmetry). All this will be preceded by a consideration about the reality status of symmetry groups s.l.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology)
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III