e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite one-dimensional periodic patterns, or friezes (sequel)
We continue our study of antisymmetry groups of friezes.
Let us derive the antisymmetry group pmg / p1g from the generating symmetry group pmg . We can do this by replacing the reflection transformation m (in the line m perpendicular to the frieze axis) by the antisymmetry transformation e1m . We let the antiidentity transformation e1 be the color permutation (Red Blue) (cycle notation). Which means that, for example, e1m is the following transformation : reflection in the line m followed by a color change between the colors red and blue.
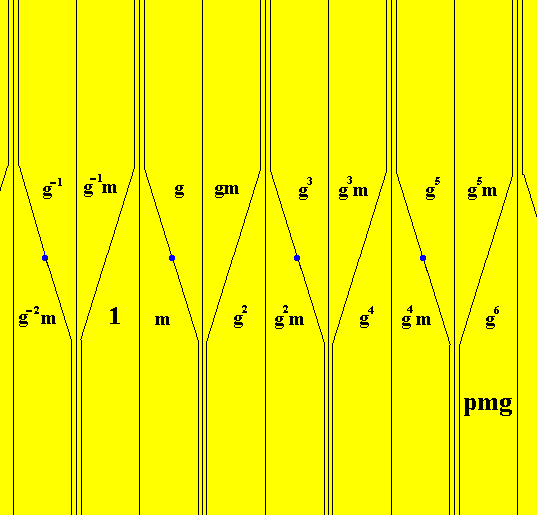
First we depict a frieze pattern according to the generating group pmg :

Figure 1. A frieze pattern according to the line group pmg . The areas representing group elements are indicated (by lines), and the blue dots represent the lattice nodes. The identities of the group elements in terms of the generators g and m are given. The pattern must be imagined to be extended indefinitely to the right as well as to the left.
The next Figure shows the result of the performed replacements.
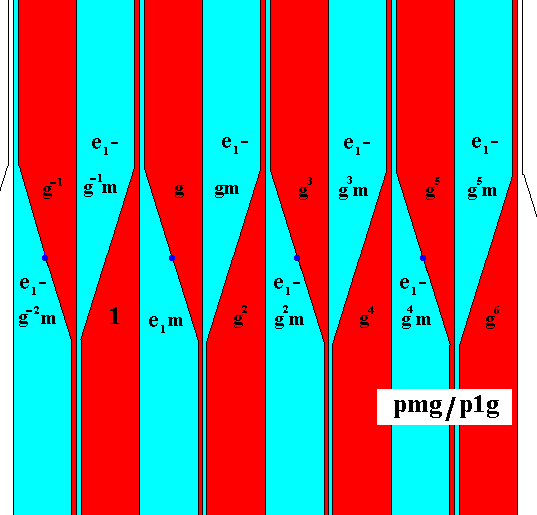
Figure 2. Pattern representing the antisymmetry group pmg / p1g , derived from the above depicted pattern representing the generating symmetry group pmg . Initial color (i.e. the color of the (area representing the) identity element) is set to be red. The antiidentity transformation e1 effects a color change from red to blue.
The set of red elements of the above Figure (containing the identity element) forms a subgroup with the symmetry of the frieze p1g . Therefore the symbol for the antisymmetry group associated with this subgroup is pmg / p1g .
The next Figure shows an example of the antisymmetry group pmg / p1g from ancient ornamental art.
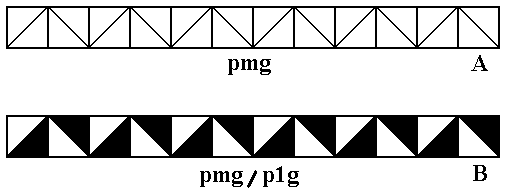
Figure 3.
Top image (A) : Pattern representing the generating symmetry group pmg .
Bottom image (B) : Antisymmetry frieze pmg / p1g in Neolithic ornamental art, Near East, around 5000 B.C. (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry group from A.
The next antisymmetry group to be derived from the line group pmg is the group pmg / p12 . It can be so derived by replacing the generator g by the antisymmetry transformation e1g , and the generator m by the antisymmetry transformation e1m . When we perform these replacements we get :
m ==> e1m .
g ==> e1g .
g2 ==> (e1g)2 = e1ge1g = e12g2 = g2 .
g3 = gg2 ==> e1gg2 = e1g3 .
etc.
g-1 ==> (e1g)-1 = g-1e1-1 = g-1e1 = e1g-1 .
g-2 = g-1g-1 ==> e1g-1e1g-1 = e12g-2 = g-2 .
etc.
Where m occurs in the symbol of a group element of the new group, the color will (again) be changed according to the permutation (Red Blue) . So we must count the color changes dictated by the g- and m-units of such elements and can then determine the color that finally results. For example the element g3m of the generating group (pmg) will become the element e1ge1ge1ge1m = e14g3m = g3m , while g2m becomes e1ge1ge1m = e1g2m .
The result of these replacements is given in the next Figure.
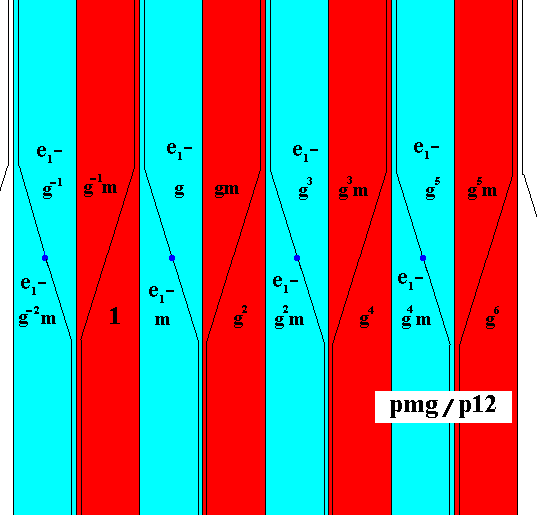
Figure 4. Pattern according to the antisymmetry group pmg / p12 derived from the generating symmetry group pmg as given in the previous Figure.
The antiidentity transformation e1 effects a color change from red to blue.
The "e1-part" must be read together with the "gm-part" or the "g-part".
When we look to the above Figure we see that the set of red elements (which contains the identity element) is a subgroup which represents the frieze p12 . Therefore the symbol of the antisymmetry group associated with this subgroup is pmg / p12 .
The next Figure shows an example of the antisymmetry group pmg / p12 in ancient ornamental art.
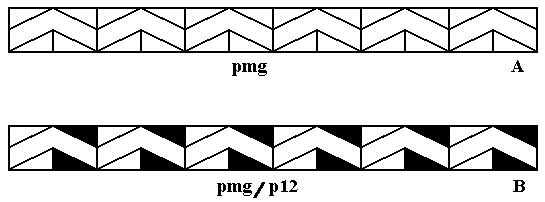
Figure 5.
Top image (A) : Pattern according to the generating symmetry group pmg .
Bottom image (B) : Antisymmetry frieze pmg / p12 in Neolithic ornamental art, Anadolia (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry group from A.
In the line group pmg we can also recognize two subgroups not associated with antisymmetry. See next Figures
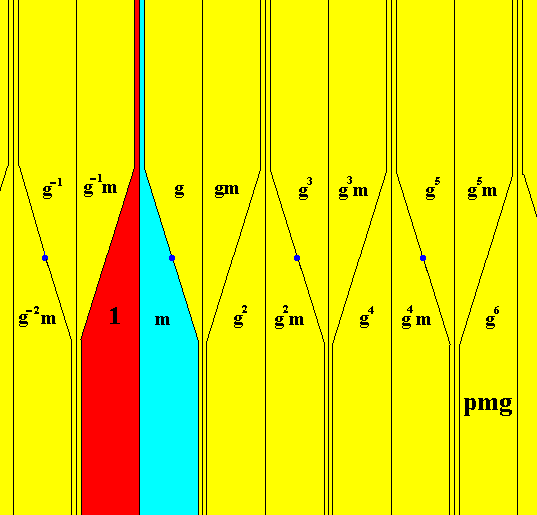
Figure 6. Subgroup {1, m} of the line group pmg . The two elements of this subgroup, related to each other by a reflection, are indicated by the red and blue colors of the areas representing these elements. The colors red and blue do not signify an asymmetry. The structure of this subgroup is D1 (isomorphic to C2 ).
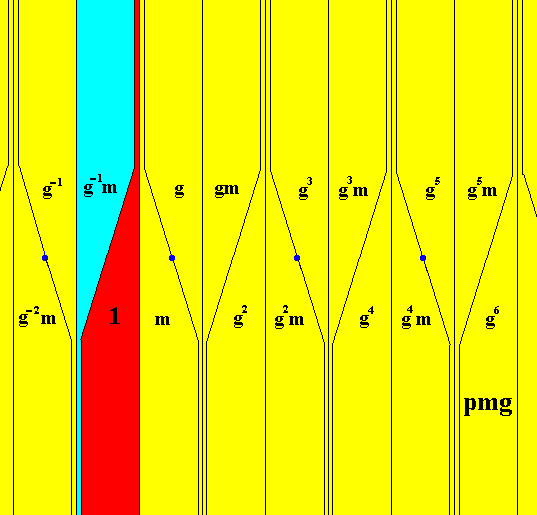
Figure 7. Subgroup {1, g-1m} of the line group pmg . The two elements of this subgroup, related to each other by a half-turn, are indicated by the red and blue colors of the areas representing these elements. The colors red and blue do not signify an asymmetry. The structure of this subgroup is C2 .
In Part II of this series we have also derived a colored symmetry group from the group pmg . See this LINK.
The next (and last) line group from which we will derive antisymmetry groups is the group pmm .
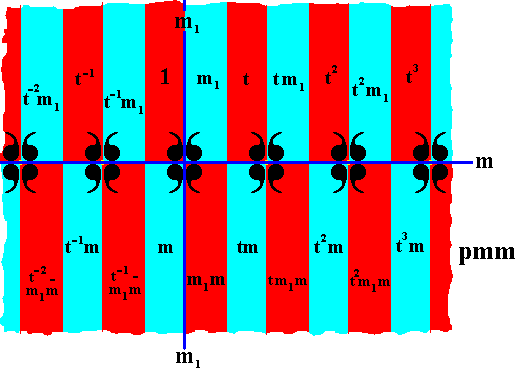
Figure 8. Frieze pattern representing the line group pmm . The areas representing group elements are marked in terms of the generators t, m, m1 . The red and blue colors do not signify any asymmetry, but only serve to higlight the areas representing group elements.
The next Figure is the same as the one above, but now with all the group element areas having the same color to express the pattern as it was before the derivation of the antisymmetry group has taken place. For this derivation , however, we'll set the initial color to be the color red.
Figure 9. Pattern representing the line group pmm . Areas representing group elements with the same color.
In the derivations below we will let the (black) commas only play a role as an aid in visualizing the symmetry of the group elements. The color changes to be made will only concern the background of those commas.
Let's now derive the antisymmetry group pmm / pmm by replacing the element t (translation) by the antisymmetry transformation e1t , and the element m1 (reflection in a line perpendicular to the frieze axis) by the antisymmetry transformation e1m1 , where we set the antiidentity transformation e1 to be the color permutation (Red Blue) (cycle notation).
In order to determine the final color of the group elements of the antisymmetry group, we count the number of e1's that will enter a group element on the basis of the just mentioned replacements. When the number is odd, one e1 is left, implying a color change. When the number is even, the e1's will cancel each other (e12 = 1 [ = no color change] ), so no color change will take place.
The next Figure shows the result of these replacements and thus gives a pattern according to the antisymmetry group pmm / pmm .
Figure 10. Pattern representing the antisymmetry group pmm / pmm , derived from the pmm pattern of the previous Figure. The antiidentity transformation effects a color change from the initial color red to the color blue.
The "e1-part" must be read together with the "tm-part" (or with the "t-part", or with the "m1-part", or with the "tm1-part", or with the "tm1m-part" or with the "m1m-part").
If we inspect the above Figure we see that the set of red elements (including the identity element) forms a subgroup that represents the frieze pmm . Therefore the symbol of the antisymmetry group associated with this subgroup is pmm / pmm .
The next Figure gives an example of the antisymmetry group pmm / pmm in ancient ornamental art.
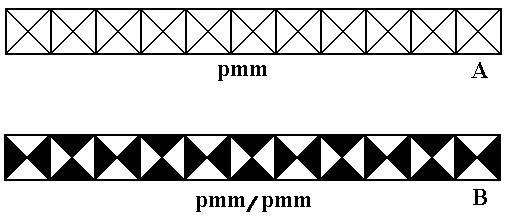
Figure 11.
Top image (A) : Pattern representing the generating symmetry group pmm .
Bottom image (B) : Antisymmetry frieze in Neolithic ornamental art, Tell el Hallaf, around 4900-4500 B.C. (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry group from A.
The next Figures explain the Neolithic frieze depicted in the above Figure.
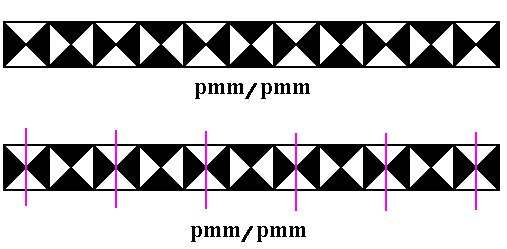
Figure 12. The lower image indicates the repeating unit of the pattern. This unit has D2 symmetry as the next Figure shows.
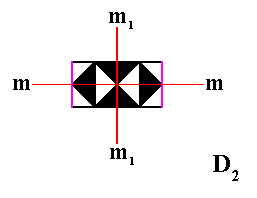
Figure 13. The repeating unit of the above depicted Neolithic frieze has D2 symmetry : It has two mirror lines, and one 2-fold rotation axis perpendicular to the plane of the pattern and passing through the intersection point of the two mirror lines.
The above Neolithic frieze pattern is a regular repetition of this D2 unit. The difference with the original generating group is that this D2 repeating unit had to be taken twice as long because of the applied antisymmetries. So the resulting antisymmetry group is still pmm and no desymmetrization has in fact occurred except for the fact that we now must take a larger symmetrical unit repeating regularly along the frieze axis.

Figure 14. Subgroup (red), having pmm symmetry, of the antisymmetry group pmm / pmm as was depicted above. Each red triangle represents two group elements, and one of these triangles consists of the identity element and the element t-1m1 . Compare with Figure10 , and see next Figure.
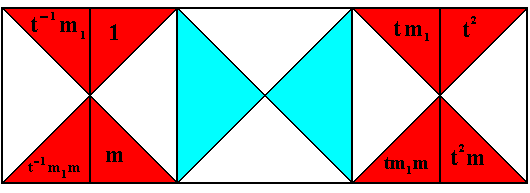
Figure 15. Eight group elements of the subgroup pmm of the antisymmetry group pmm / pmm .
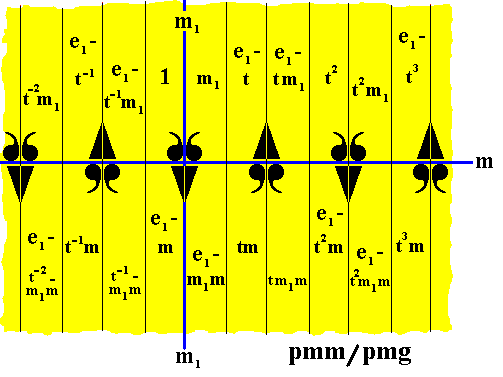
The next antisymmetry group to be derived from the symmetry group pmm is the group pmm / pm1 . It can be accomplished by replacing the element m by the antisymmetry transformation e1m . The next Figure shows the result.
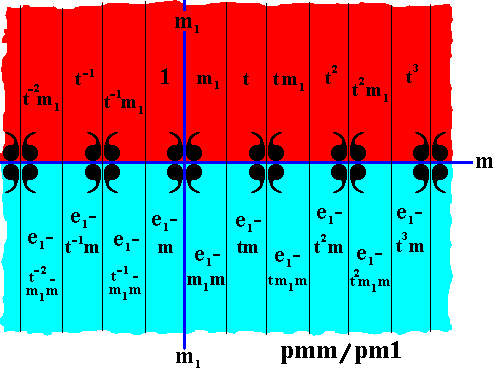
Figure 16. Pattern representing the antisymmetry group pmm / pm1 , derived from the symmetry group pmm . The initial color is set to be the color red. The antiidentity transformation e1 effects a change from red to blue. The reading of the group elements should be done as indicated in the foregoing.
As can be seen in the above Figure, the set of red elements (containing the identity transformation) represents the frieze pm1 . Therefore the symbol of the antisymmetry group associated with this subgroup is pmm / pm1 .
As an example of the antisymmetry group pmm / pm1 in Neolithic ornamental art, see next Figure.
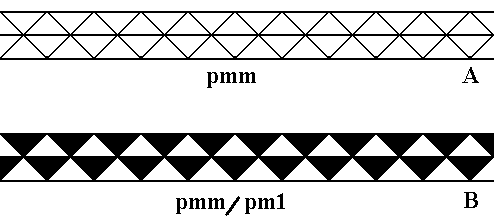
Figure 17.
Top image (A) : Pattern representing the generating symmetry group pmm .
Bottom image (B) : Antisymmetry frieze pmm / pm1 in Neolithic ornamental art, Hacilar, about 5500-5200 B.C. (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry group from A.
The just depicted Neolithic frieze needs some explanation.
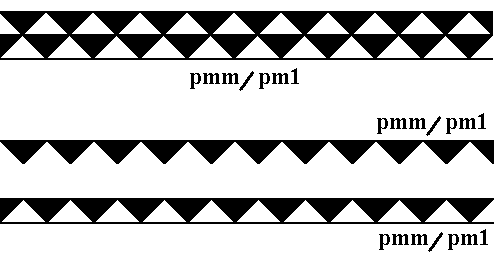
Figure 18. The Neolithic frieze depicted above consists of two layers, each representing the antisymmetry group pmm / pm1 .
Although there is a repetition of a basic frieze in this Neolitic frieze, in the direction perpendicular to the frieze axis, this is only a matter of two layers. So there is no indefinite repetition in that direction. There is thus only one direction in which indefinite repetition takes place, and so our pattern is still a frieze.
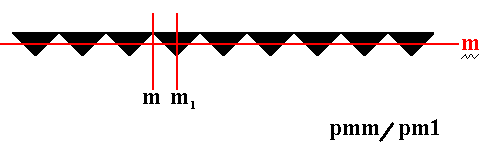
Figure 19. A layer of the Neolithic frieze depicted above.
It has two mirror lines perpendicular to the frieze axis. Because of the color change the mirror line m coinciding with the frieze axis has disappeared, transforming the pattern into a pm1 frieze. But when interpreted as antisymmetry group the 'flip-flop' character -- typical for a period 2 group element like a reflection -- is restored, resulting in the pattern to be a pmm frieze again (but not the same as the generating group, because the flip-flop is now provided by another transformation).
The next antisymmetry group to be derived from the generating symmetry group pmm is the group pmm / pmg . It can be accomplished by replacing the element m (reflection in the frieze axis) by the antisymmetry transformation e1m , and of the element t (translation) by the antisymmetry transformation e1t . The antiidentity transformation e1 is again the permutation (Red Blue) (cycle notation). The result of the displacement can be seen in the next Figure.
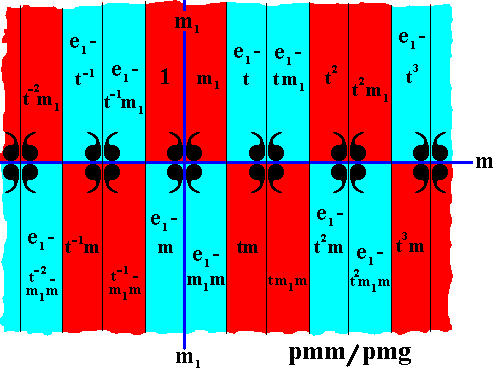
Figure 20. Pattern representing the antisymmetry group pmm / pmg , derived from the pmm pattern of Figure 9. The initial color is set to be the color red. The antiidentity transformation e1 changes this color into blue. The group element symbols must be read as was indicated in the foregoing.
As can be seen in the above Figure, the set of red elements (containing the identity element) forms a subgroup representing the frieze pmg . Therefore the symbol for the antisymmetry group associated with this subgroup is pmm / pmg .
In our pattern of the line group pmm we can detect three subgroups not associated with antisymmetry. Two of them have the structure of D1 (which is isomorphic to C2 ), and one has the structure of D2 . See next three Figures.
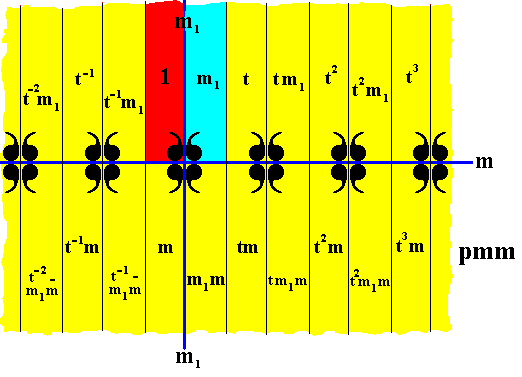
Figure 21. Subgroup {1, m1} of the group pmm , with D1 structure. The colors red and blue do not signify asymmetry but only serve to indicate the two group elements of the subgroup.
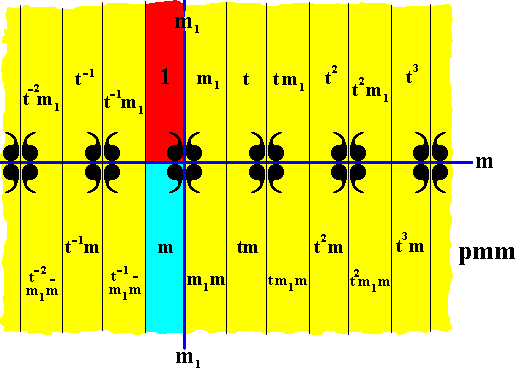
Figure 22. Subgroup {1, m} of the group pmm , with D1 structure. The colors red and blue do not signify asymmetry but only serve to indicate the two group elements of the subgroup.
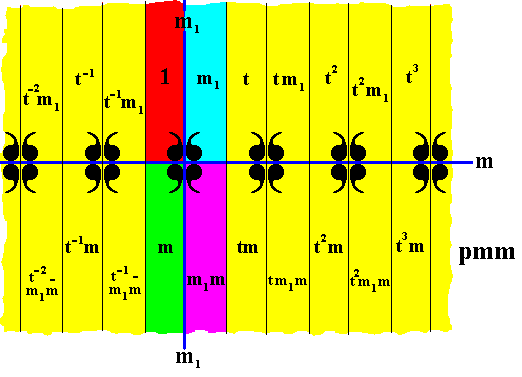
Figure 23. Subgroup {1, m1, m, m1m} of the group pmm , with D2 structure. The colors red, green, purple and blue do not signify asymmetry but only serve to indicate the four group elements of the subgroup.
Discussion of antisymmetry friezes
It is interesting to dwell a little longer on the last antisymmetry group pmm / pmg , depicted in Figure 20. For convenience we give it again :
Figure 24. ( = Figure 20) Pattern representing the antisymmetry group pmm / pmg , derived from the pmm pattern of Figure 9. The initial color is set to be the color red. The antiidentity transformation e1 changes this color into blue. The group element symbols must be read as was indicated in the foregoing.
In all the above discussions the antiidentity transformation e1 was interpreted as the color permutation (Red Blue) . But recall that this transformation can be interpreted as standing for any bivalent quality, geometric or not. Let us think of the pmm pattern as a (projection of a) row of chemical units as part of a real crystal. And let us then think of the bivalent quality "being atomic complex A or being atomic complex B " [An atomic complex is a chemical unit consisting of several atoms chemically bonded to each other]. We can then interpret the antiidentity transformation e1 as a change from A to B, i.e. the replacement of atomic complex A by the atomic complex B, but only there where e1 is actually applied. This means that the blue areas in the above Figure (Figure 24) now express the fact that there the atomic complex, represented by the red areas -- the atomic complex A -- is replaced by the atomic complex B. Let's show these (fictitious) atomic complexes A and B :

Complex A as well as complex B consists of two units mirror symmetric with respect to each other. Such a unit is a comma in the original case, while it is a rectangular triangle in the derived case.
We will now replace the color change red ==> blue by a change from atomic complex A to atomic complex B , i.e. the meaning of the antiidentity transformation e1 now becomes this latter change, which in turn means that we now have to do with the chemical permutation (A B) (cycle notation). This chemical permutation must, however, be specified a little further : Each original atomic complex consists of two halves (commas) that are mirror symmetric with respect to each other, and each half will be replaced by an asymmetric rectangular triangle in the following way, that is to say we now specify exactly the just mentioned chemical replacement (i.e. the new interpretation of e1 ) :
If the new group element (i.e. the group element of the resulting antisymmetry group) contains a e1 , then the corresponding comma expressing the original group element (and which is one half of the original atomic complex) must be replaced by a (specified) rectangular (black) triangle (representing one half of the atomic complex B). The orientation of the rectangular triangle in the following way depends on the orientation of the original comma :
If the orientation of the comma is this :
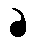
then it must be replaced by
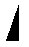
But if the orientation of the comma is this :
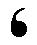
then it must be replaced by
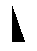
If, on the other hand, the orientation of the comma is this :
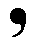
then it must be replaced by
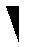
And, if, finally, the orientation of the comma is this :
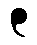
then it must be replaced by
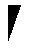
All this can now stand for the chemical permutation (A B) .
The result is given in the next Figure.
Figure 25. Re-interpretation of the antiidentity transformation e1 , from the color permutation (Red Blue) (cycle notation) to the chemical permutation (A B) (cycle notation), applied to the pmm / pmg pattern of Figure 24.
Now we can say the following : We initially have a pattern, according to the group pmm , which is isomorphic to the abstract group Dinfinity x D1 . And this pattern consists of atomic complexes A only :
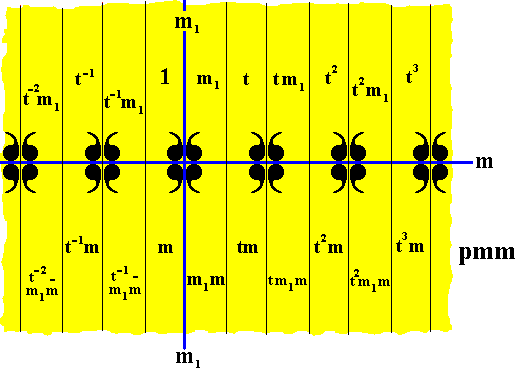
Figure 26. Pattern, consisting of atomic complexes A, according to the line group pmm .
Then we simply alternately replace -- not yet involving antisymmetry transformations -- atomic complex A by atomic complex B , resulting in a pattern according to the group pmg , which is isomorphic to the abstract group Dinfinity , and clearly is a case of symmetry-breaking :
Figure 27. Symmetry-breaking of the above pmm pattern, to a pattern according to the line group pmg .
This pattern is isomorphic to the subgroup pmg of the group pmm as the next Figure shows.
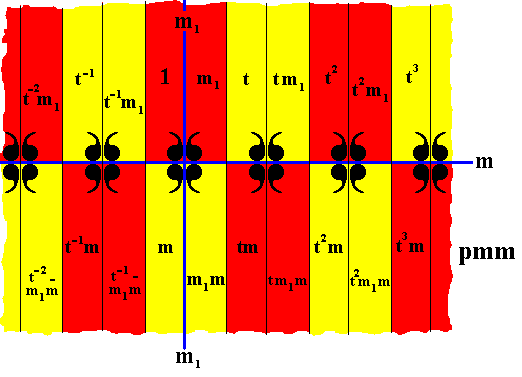
Figure 28. The subgroup pmg (red) of the group pmm . This subgroup is isomorphic to the pattern of Figure 27.
But when we now interpret the pattern of Figure 27, with its alternation of atomic complexes, as an antisymmetry group, derived from the group pmm , where the identity transformation e1 stands for a replacement of atomic complex A by atomic complex B , as specified above, we get the (antisymmetry) group pmm / pmg , which is isomorphic to the group pmm , and thus isomorphic to the abstract group Dinfinitu x D1 again :
which was already shown in Figure 25.
So in the context of ordinary symmetry, an alternate replacement of atomic complex A by atomic complex B results in the symmetry-breaking :
Dinfinity x D1 ==> Dinfinity . But when this symmetry-breaking result is interpreted as the antisymmetry group pmm / pmg we have not a case of genuine symmetry-breaking anymore.
So the theory of antisymmetry in this case, i.e. in the case of patterns according to the line group pmm , shows that the alternating replacements of a mirror-symmetric atomic complex by another mirror-symmetric atomic complex, does not result in a change of the basic symmetry structure. Of course there has been changed something (as a result of the mentioned replacements -- chemical substitutions ), and this is expressed by the transition from the original group pmm to the antisymmetry group pmm / pmg , i.e. by a transition from a symmetry group to an antisymmetry group. So the antisymmetry theory in this case shows a very close symmetry kinship between the homogeneous chemical sequence of atomic complexes A, and the alternating chemical sequence of atomic complex A and B. Similar considerations can be applied to the other antisymmetry friezes.
The next table summarizes all the possible antisymmetry groups derivable from the seven frieze types.
| Frieze | Antisymmetry frieze |
| p11 | p11 / p11 |
| p1g | p1g / p11 |
| p12 | p12 / p12, p12 / p11 |
| pm1 | pm1 / pm1, pm1 / p11 |
| p1m | p1m / p1m, p1m / p1g, p1m / p11 |
| pmg | pmg / pm1, pmg / p12, pmg / p1g |
| pmm | pmm / pmm, pmm / pmg, pmm / p1m, pmm / pm1, pmm / p12 |
This concludes our exposition of Friezes and of the antisymmetry groups that can be derived from them.
The next document will start our study of antisymmetry groups derived from ornaments G2 , i.e. derived from the 17 Plane Groups.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology)
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV
Back to subpatterns and subgroups Part V