e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite two-dimensional periodic patterns, or Ornaments (sequel)
The next plane group to be discussed with respect to the interpretation of the center of the motif s.str. is the group Cm .

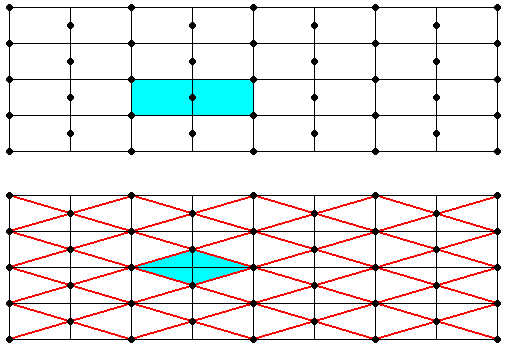
Figure 1. A centered rectangular lattice (top image) is equivalent to a (primitive) rhombic lattice (diamond net) (bottom image, red lines). In both images a unit mesh is indicated (blue).
The next Figure shows these same lattices, but now with most auxiliary lines removed, so that these lattices come out clearly.
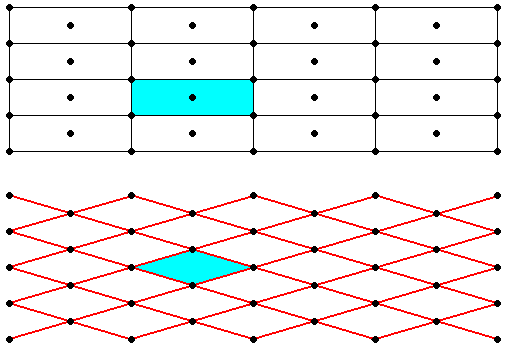
Figure 1a. Centered rectangular point lattice (top image), and (primitive) rhombic point lattice. Both lattices are equivalent.
First the group Cm can be represented by the following pattern :
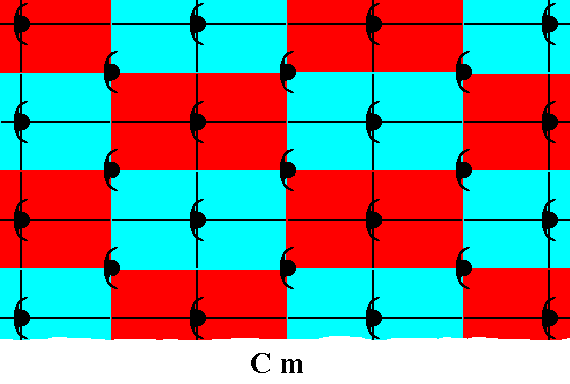
Figure 2. A pattern according to the plane group Cm .
The centered rectangular point lattice is indicated. A motif s.str. with symmetry D1 is present at each lattice point (which here means at the corners of the lattice mesh as well as at the center of the mesh).
The next Figure shows the possible rhombic lattice underlying the Cm pattern of the above Figure.
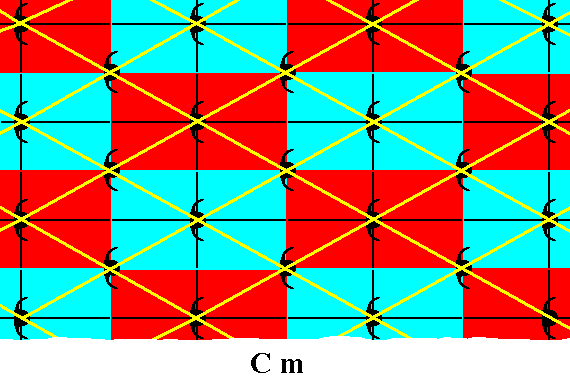
Figure 3. Rhombic point lattice of the Cm pattern of the previous Figure.
Isolating a rhombic mesh from the above Cm pattern reveals that the content of such a rhombus contains units of the motifs s.str. together having D1 symmetry (one horizontal mirror line as its only symmetry element). And this means that we can depict the Cm pattern by simply putting a figure with D1 symmetry in the center of each rhombic mesh. See next Figure.
Figure 4. The content of each rhombic lattice mesh of the above Cm pattern has D1 symmetry.
The next Figure shows the rhombic lattice, with a D1 motif placed in each mesh, and as such representing the plane group Cm .
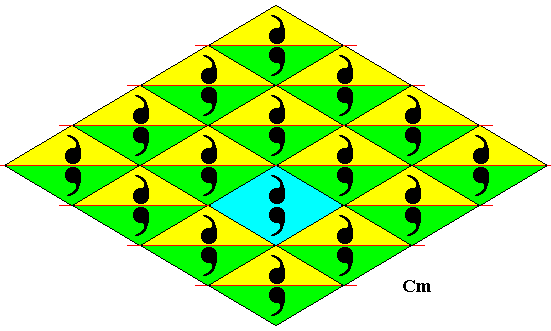
Figure 5. Pattern representing plane group Cm . The motifs s.str. are (chosen to be) a set of two commas, and as such placed inside the lattice meshes. The commas in a mesh are related to each other by a horizontal reflection line. Half of a rhombic lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit (comma) of the motif s.str. . A lattice mesh is indicated (blue). The pattern must be imagined to extend indefinitely over the plane.
The next plane group to be investigated is the group C2mm .
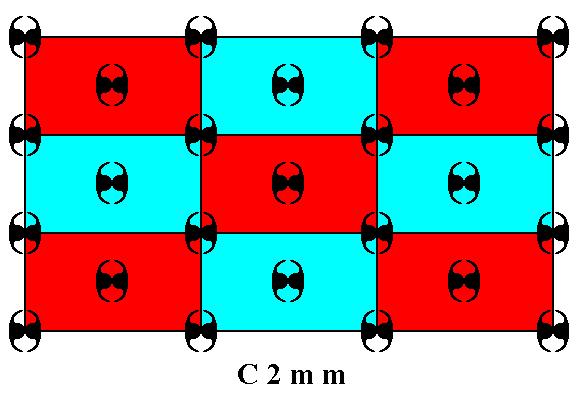
Figure 6. A pattern representing the plane group C2mm .
The centered rectangular lattice is indicated. Each lattice node holds a rosette of the symmetry group D2 , which is considered to be the motif s.str. of the pattern.
When we view -- in the above Figure -- the motifs s.str. as having their centers at the mid-points of the lattice meshes, i.e. if we look to the symmetry of the contents of a lattice mesh, we see a D2 symmetry, as the next Figure illustrates.

Figure 6a. Isolated unit mesh of the C2mm pattern of Figure 6. Its contents has D2 symmetry.
If we isolate a rhombic mesh, we see that the content also has D2 symmetry, i.e. it has two mirror lines perpendicular to each other (and a 2-fold rotation axis going through their intersection point). See next Figure.
Figure 7. The content of a rhombic lattice mesh of the C2mm pattern depicted above, has D2 symmetry.
Knowing that the content of a rhombic lattice mesh has D2 symmetry, we can, in order to depict the C2mm pattern, simply put a motif with D2 symmetry in the mid-point of each rhombic lattice mesh. See next Figure.
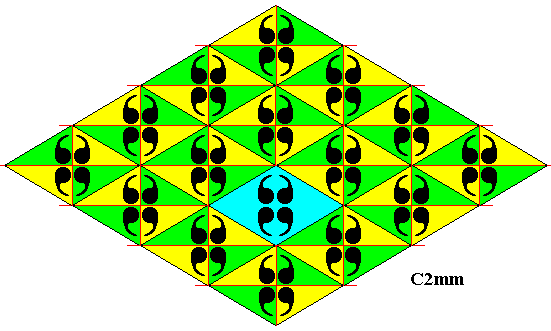
Figure 8. Pattern representing plane group C2mm . The motifs s.str. are (chosen to be) a set of four commas, and as such placed inside the (rhombic) lattice meshes. The commas in a mesh are related to each other by horizontal and vertical reflection lines. A quarter of a rhombic lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit (comma) of the motif s.str. . A lattice mesh is indicated (blue). The pattern must be imagined to extend indefinitely over the plane.
The next plane group to be considered is the group P4 . It is based on a square lattice. Usually we have considered 4-fold motifs s.str. as consisting of four (partly overlapping) commas. The centra of these motifs were viewed as coinciding with lattice points :
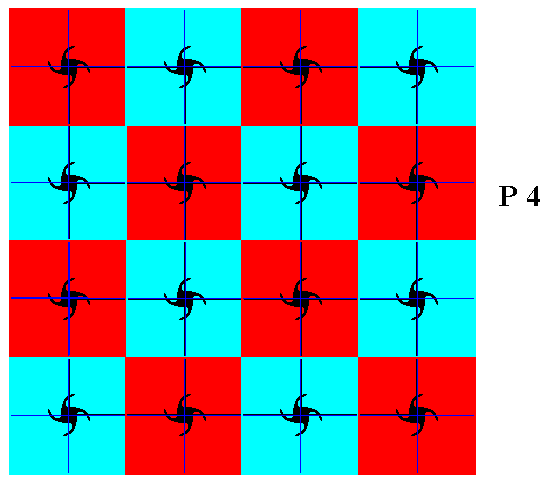
Figure 9. A pattern representing the plane group P4 . Four-fold rosettes are placed at the lattice points of the square lattice.
When we isolate a (square) lattice mesh, we get the following :

Figure 10. A lattice mesh isolated from the above P4 pattern.
As we can see in the above Figure, the content of a lattice mesh has C4 symmetry, with the 4-fold rotation axis going through the center of the mesh. So in setting up the P4 pattern we can just as well place a C4 motif in the center of each lattice mesh. See next Figure.
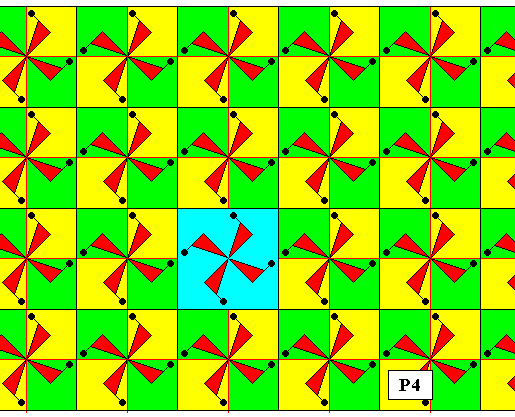
Figure 11. Pattern representing plane group P4 . The motifs s.str. are (chosen to be) a set of four vanes, and as such placed inside the (square) lattice meshes. The vanes in a mesh are related to each other by a 4-fold rotation axis. A quarter of a square lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit (vane) of the motif s.str. . A lattice mesh is indicated (blue). The pattern must be imagined to extend indefinitely over the plane.
The next plane group to be considered is the group P4mm . Patterns representing this group are also based on a square lattice. Usually we have considered the D4 motifs s.str. as consisting of eight (partly overlapping) commas. The centra of these motifs were viewed as coinciding with lattice points :
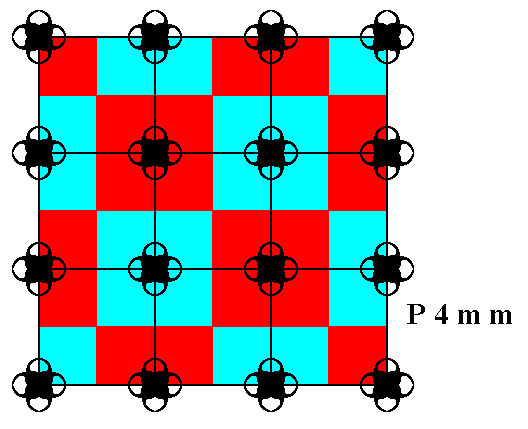
Figure 12. A pattern representing the plane group P4mm . D4 rosettes are placed at the lattice points of the square lattice. The colors red and blue do not signify symmetry features, but serve to highlight the motifs s.l.
When we isolate a (square) lattice mesh, we get the following :
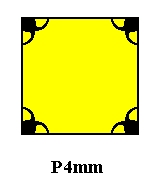
Figure 13. A lattice mesh isolated from the above P4mm pattern.
As can be seen from the above Figure, the content of the lattice mesh of the P4mm pattern has D4 symmetry. So in setting up a P4mm pattern we can just as well place a D4 motif in the center of each lattice mesh. See next Figure.

Figure 14. Pattern representing plane group P4mm . The motifs s.str. are (chosen to be) a set of eight units, and as such placed inside the (square) lattice meshes. The units in a mesh are related to each other by a 4-fold rotation axis and two pairs of mirror lines. One eighth of a square lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit of the motif s.str. . A lattice mesh is indicated (blue). The pattern must be imagined to extend indefinitely over the plane.
The next plane group to be discussed is the plane group P4gm . Its patterns are also based on a square lattice. Usually we have depicted such a pattern as follows :
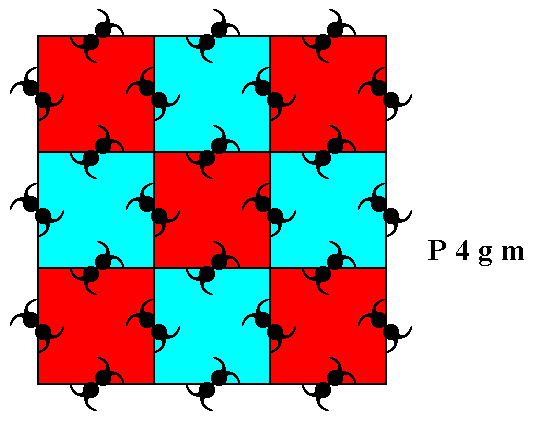
Figure 15. Pattern representing plane group P4gm . At the mid-point of each side of a lattice mesh there is a motif s.str. with D2 symmetry, i.e. a figure having two mirror lines perpendicular to each other and a 2-fold rotation axis through their point of intersection.
The next Figure shows a (square) lattice mesh and its contents.

Figure 16. Isolated lattice mesh of the P4gm pattern of the previous Figure.
In the above Figure we see four units of motifs s.str. related to each other by a 4-fold rotation with the rotation axis going through the center of the mesh. But these units are not asymmetric figures. Each one of them is mirror symmetric, in such a way that the mirror lines are parallel to (but not incident with) the diagonals of the lattice mesh. Further they are related to each other by glide lines that are parallel to (but not incident with) the sides of the lattice mesh. The next Figure illustrates this.
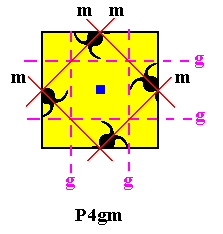
Figure 17. Symmetry of the content of a lattice mesh of the P4gm pattern depicted above. Mirror lines are indicated by solid red lines, glide lines by purple dashed lines, and the 4-fold rotation axis by a small blue square.
At the corners of the lattice mesh there are also 4-fold rotation axes (not indicated). Further there are half-turns at the mid-points of the sides of the lattice mesh.
The next Figure depicts a P4gm pattern with the appropriate motif s.str. inside each lattice mesh.
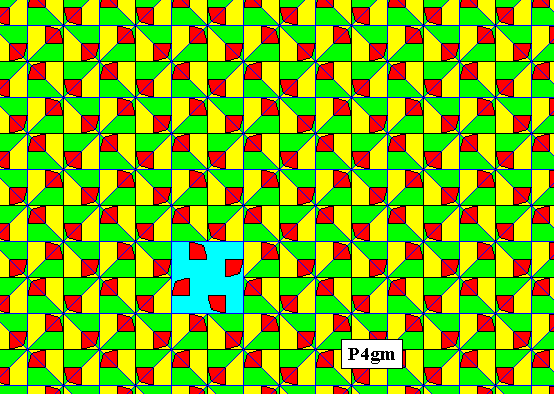
Figure 18. Pattern representing plane group P4gm . The motifs s.str. are (chosen to be) a set of four units, and as such placed inside the (square) lattice meshes. The units in a mesh are related to each other by a 4-fold rotation axis and two pairs of glide lines and two pairs of mirror lines. One eighth of a square lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit of the motif s.str. . A lattice mesh is indicated (blue). The pattern must be imagined to extend indefinitely over the plane.
The next two Figures show some of the mirror lines and some of the glide lines of the P4gm pattern.
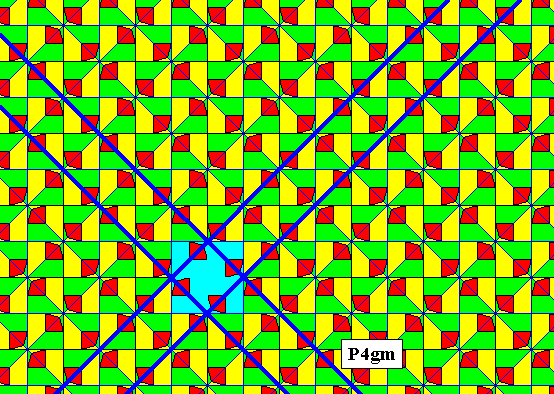
Figure 19. Some reflection lines are indicated in the P4gm pattern of Figure 18.
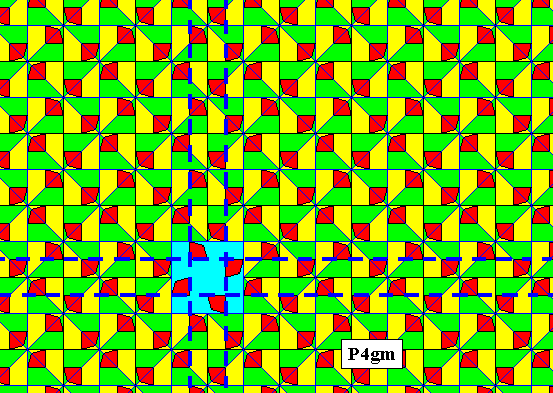
Figure 20. Some glide lines are indicated in the P4gm pattern of Figure 18.

Figure 21. Some half-turns (small solid ellipses) and one 4-fold rotation axis (small solid square) are indicated in the P4gm pattern of Figure 18.
The next Figure, finally, shows the presence of 4-fold rotations at the corners of a mesh (i.e. at every lattice node), and one such axis at its center.
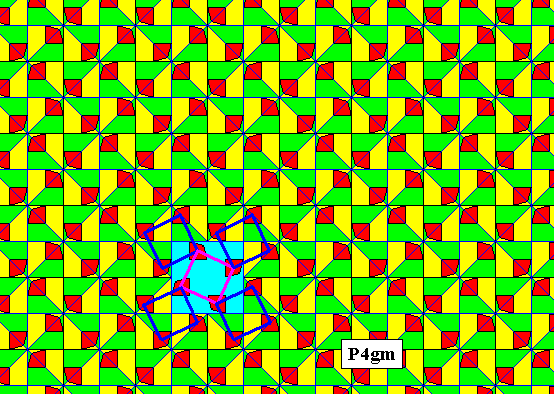
Figure 22. At each lattice point of our P4gm pattern there is a 4-fold rotation axis as well as at the center of each (square) lattice mesh.
All the above shows that our pattern is indeed a genuine P4gm pattern.
In the next document we will continue our investigation into the interpretation of the motifs s.str. in the plane group patterns.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology)
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV
Back to subpatterns and subgroups Part V
Back to subpatterns and subgroups Part VI
Back to subpatterns and subgroups Part VII
Back to subpatterns and subgroups Part VIII