
e-mail :

Sequel to Group Theory
As always, we start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite two-dimensional periodic patterns, or Ornaments (sequel)
In the previous document we have investigated antisymmetry patterns, and subpatterns representing-, and subpatterns-not-representing subgroups, all derivable from Cm patterns.
Antisymmetry ornament derivable from a Cm pattern in Neolithic art.
We first give and analyse the Cm pattern from which the neolithic antisymmetry ornament may be derived.
Figure 1. Generating Cm symmetry pattern from which may be derived an antisymmetry pattern present in Neolithic art.
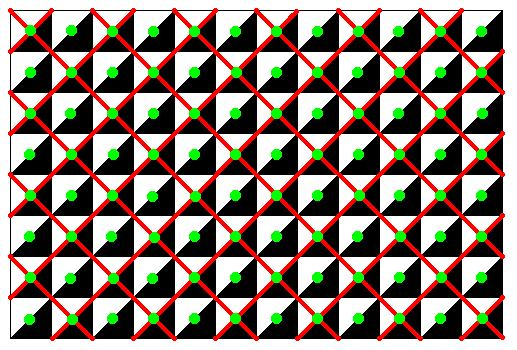
Figure 2. Point lattice (indicated by the green points and red connection lines) of the generating Cm symmetry pattern. It is a centered rectangular lattice (lattice points at the corners as well as in the center of each mesh) : It is not a quadratic lattice (despite the fact that the shape of a mesh is a square) because the motifs associated with the lattice points have only D1 symmetry, and not D4 or C4 symmetry (and also not D2 for that matter). And a D1 motif is not compatible with a square lattice. See next Figures.

Figure 3. Generating Cm pattern and its lattice (as in previous Figure). Five motifs highlighted to show the equivalence of the lattice points.

Figure 4. The five motifs highlighted in the previous Figure isolated to show the lattice structure (centered rectangular lattice) and lattice point equivalence ( The central point is seen to be equivalent to the four corner points, i.e. they have identical surroundings).
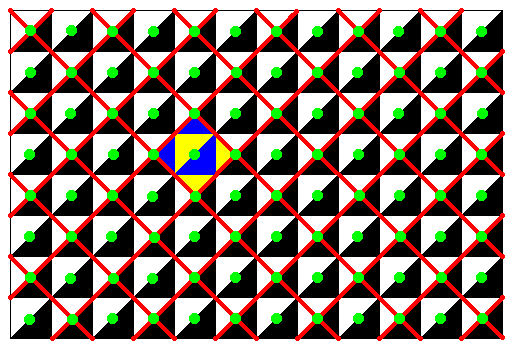
Figure 5. Generating Cm pattern and its lattice. A unit mesh is indicated (See also next Figure).

Figure 6. Unit mesh of the generating Cm pattern, as indicated in the previous Figure, isolated. Its five lattice points are indicated by the color green (A point at each corner and a point in the center).
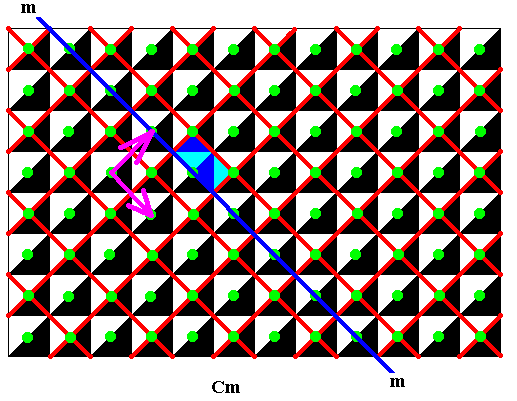
Figure 7. Generating Cm pattern and its lattice (centered rectangular lattice, as in previous Figure). One group element is highlighted. It is represented by a rectangular asymmetric motif. When we set this group element to be the identity element, we can generate the whole group (Cm) by first reflecting the (area representing the) identity element in the line m (which we have chosen to represent the generating reflection). We have now two group elements. If we subject both group elements to the two generating translations (indicated by purple arrows) we get the whole pattern.
The same Cm pattern can also shown to be based on a rhombic lattice , as the next Figure shows.

Figure 8. Generating Cm pattern equivalently based on a r h o m b i c lattice. (indicated by red connection lines). It is not a square lattice -- despite the meshes having the outline of a square -- (and even not a primitive rectangular lattice), because the D1 motifs are not compatible with a square lattice (nor, because of the way they are repeated here, with a p r i m i t i v e rectangular lattice [ They are, as we have seen, compatible with a c e n t e r e d rectangular lattice.]). A unit mesh is indicated.
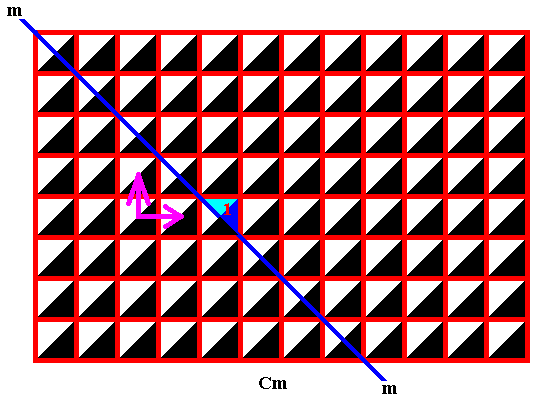
Figure 9. Generators associated with the rhombic lattice of the above Cm pattern :
m .
If we reflect the identity element 1 (the area representing it being indicated) in the line m we get two elements in all. When we subject these to the translations indicated by the purple arrows, we obtain the whole Cm pattern.
Now we're going to derive from the above Cm pattern an antisymmetry pattern that is found in Neolithic art.
NOTE :
In what follows we will try to derive this antisymmetry pattern. It is depicted in Figure 16, and is claimed by JABLAN, 2002, Symmetry, Ornament and Modularity, p. 144, fig. 2.107 (j), to represent the antisymmetry group Cm / Pm . However, as we will see, the Neolithic ornament, although representing a group, namely the plane group P1 , does not represent an antisymmetry group at all. The ornament does not possess any reflections nor any antisymmetry reflections. With respect to the generating Cm pattern it has lost all reflections, without them being replaced by antisymmetry transformations. The translations are replaced by their corresponding antisymmetry translations, where the antiidentity transformation e1 must be interpreted as a permutation between two configurations, Solid - Striped (See below). This results in a horizontal and vertical alternation of the mentioned configurations.
If we want to generate the alleged antisymmetry pattern, starting with the (area representing the) identity element of the generating symmetry patttern as well as of the alleged antisymmetry pattern, we only have the horizontal and vertical antisymmetry translations, and with them we cannot generate the whole pattern, but only a part of it. This means that the neolithic ornament is not representing an antisymmetry group, but just a symmetry group, namely -- as has been said -- the plane group P1.
Nevertheless it will be worth trying to derive the neolithic ornament as an antisymmetry pattern from an initial Cm pattern. It is worth trying, because it is very instructive, as to realize what antisymmetry patterns are and what they are not.
Having said this, we will now continue the derivation.
The antiidentity transformation e1 will be interpreted as the permutation of two configurations :
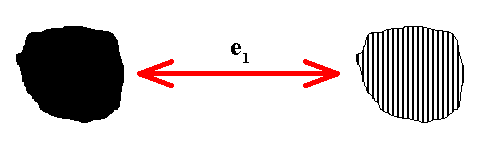
Figure 10. Interpretation of the antiidentity transformation e1 as the permutation (Solid, Striped) (cycle notation) with respect to the color black (as present in the above generating Cm pattern (Figure 1 )).
In order to derive the (alleged) antisymmetry pattern from the Cm pattern of Figure 1 we replace both translations -- as they are indicated in Figure 9 -- by their corresponding antisymmetry transformations. Such an antisymmetry translation goes as follows : Take a group element (as indicated in Figure 9 ), translate it, and then change solid black into vertical stripes, or vertical stripes into solid black :
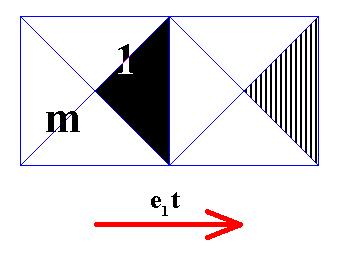
Figure 11. Effect of the antisymmetry translation e1t when applied to the (area representing the) identity element (1) of the above given generating Cm symmetry pattern. The element m is indicated, coloring omitted.
The next Figure depicts the same as the previous Figure did, but with emphasis on the (areas representing the) group elements involved.
Figure 12. Effect of the antisymmetry translation e1t when applied to the (area representing the) identity element (1) of the above given generating Cm symmetry pattern. In this Figure the boundaries of the two group elements involved ( 1 and e1t ) are precisely delineated. Both areas representing these group elements have a triangular shape (with its right angle at its upper-right corner) and consist either of a black part and a white part -- blue in the Figure -- (As such, with respect to the color configuration mentioned : all elements of the generating symmetry pattern), or of a black-or-of-a-striped part and a white part -- blue in the Figure -- (As such, with respect to the color configurations mentioned : elements of the antisymmetry pattern).
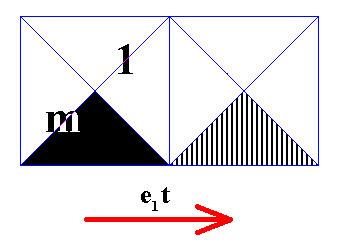
Figure 13. Effect of the antisymmetry translation e1t when applied to the (area representing the) element m of the above given generating Cm symmetry pattern. The element 1 (identity element) is indicated, coloring omitted.
The element m was obtained by reflecting the identity element in the south-east diagonal of the square (which diagonal is the generating reflection line of the initial Cm pattern). But this line is no longer a reflection line of the whole resulting (alleged) antisymmetry pattern, which means that we cannot generate the element m as a stage in the generation of the alleged antisymmetry pattern.
The next Figure depicts the same as the previous Figure did, but with emphasis on the (areas representing the) group elements involved.
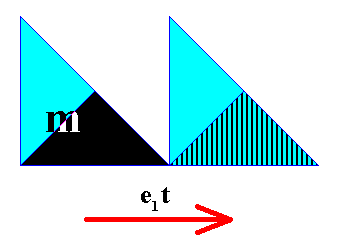
Figure 14. Effect of the antisymmetry translation e1t when applied to the (area representing the) element m of the above given generating Cm symmetry pattern. In this Figure the boundaries of the two group elements involved ( m and e1tm ) are precisely delineated. Both areas representing these group elements have a triangular shape (with its right angle at its bottom-left corner) and consist either of a black part and a white part -- blue in the Figure -- (As such, with respect to the color configuration mentioned : all elements of the generating symmetry pattern), or of a black-or-of-a-striped part and a white part -- blue in the Figure -- (As such, with respect to the color configurations mentioned : elements of the antisymmetry pattern).
The next Figure gives the combined effect of the antisymmetry translation when applied to both elements 1 and m .
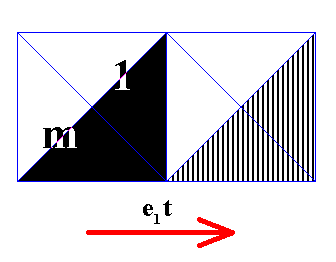
Figure 15. Effect of the application of the antisymmetry translation (horizontal) e1t to the elements 1 and m of the generating Cm pattern.
All what we have said above with respect to the horizontal antisymmetry translation also applies to the vertical antisymmetry translation. The described configurations (solid, striped) will alternate in the horizontal and vertical directions (because e1te1t = e1e1tt = tt = t2 ).
We further see that replacing both translations by their corresponding antisymmetry translations, automatically i m p l i e s the elimination of the generating relection m and all other reflections parallel to it.
On the basis of all this we can now draw the (alleged) antisymmetry pattern :
Figure 16. Alleged antisymmetry pattern Cm / *Pm derived from the generating Cm symmetry pattern of Figure 1 by replacing both translations, as indicated in Figure 9, by their corresponding antisymmetry transformations as defined above.
After JABLAN, 2002.
Let's analyse this antisymmetry pattern.

Figure 17. Point lattice (indicated by red connection lines) of the (alleged) antisymmetry pattern Cm / *Pm of the previous Figure.

Figure 18. Point lattice (indicated by red connection lines) of the (alleged) antisymmetry pattern Cm / *Pm of Figure 16. A unit mesh is indicated (by alternative colors).
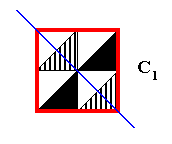
Figure 19. Unit mesh of the above (alleged) antisymmetry pattern isolated.
This unit mesh is not symmetric in the indicated diagonal line. Indeed, it doesn't have any symmetry at all (meaning that it represents the point group C1 ).
The (alleged) antisymmetry pattern (consisting of a repetition of this unit cell), if not interpreted as representing an antisymmetry group, but just a symmetry group, thus consists of an asymmetric motif that is repeated by two independent translations. So its symmetry is according to the plane group P1 . But, interpreted as representing an antisymmetry group (where the translations of the generating symmetry group are replaced by antisymmetry translations), the (algebraic) structure of the antisymmetry pattern n o r m a l l y would be isomorphic with that of the corresponding generating symmetry pattern, and thus, in the present case, with the plane group Cm . But, because, by replacing both translations by antisymmetry translations, the mirror lines, originally present in the generating Cm pattern, have vanished, the resulting antisymmetry pattern c a n n o t be isomorphic to the latter, and is therefore not an antisymmetry pattern at all.
The next Figure gives an alternative point lattice that is preferable to the one in the above Figures, because its meshes are smaller.

Figure 19a. Alternative and preferable point lattice (indicated by red connection lines) of the pattern of the above Figures (16, 17, 18). It has a smaller unit mesh. The content of the latter is not symmetric.
If we now isolate all elements of the (alleged) antisymmetry pattern that are not the result of an antisymmetry transformation, we get the following subpattern :
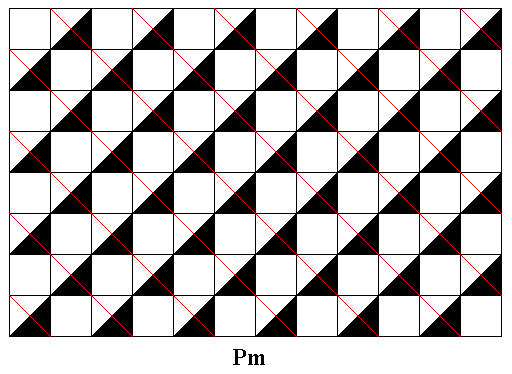
Figure 20. Subpattern resulting from isolating all elements of the above derived (alleged) antisymmetry pattern that are not the result of an antisymmetry transformation (for example the element e1te1t = t2 , and also, of course, the identity element).
The pattern of Figure 20 has clearly Pm symmetry.
The next three Figures indicate the areas representing group elements as was the case in the generating Cm pattern.

Figure 21. Areas representing group elements (separated by red lines) -- with respect to the isolated subpattern -- as we recognize them also in the generating Cm pattern (Figure 1 and Figure 9 ).
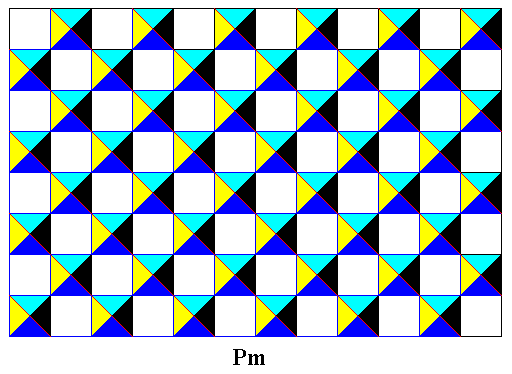
Figure 22. Areas representing group elements (separated by red lines, and indicated by different coloration) -- with respect to the isolated subpattern -- as we recognize them also in the generating Cm pattern (Figure 1 and Figure 9 ). Coloration : One group element consists of a black and a white subarea (here indicated as black and light blue), another consists also of a black and a white subarea (here indicated as dark blue and yellow). See next Figure.

Figure 23. Two elements, A and B , of the above isolated subpattern.
The isolated subpattern has infinitely many mirror lines of two types as the next Figure shows.
Figure 24. The isolated subpattern (of the above derived (alleged) antisymmetry pattern) has infinitely many parallel reflection lines. Two of them (one of each type) are highlighted (purple).
The next Figures show how the subpattern (having Pm symmetry) can be generated. The (area representing the) identity element here chosen can be interpreted as the identity element of the generating Cm symmetry pattern as well.
Figure 25. Generation of the element m by reflecting the identity element ( 1 ) in the line m , which is chosen to represent the generating reflection of the subpattern.
Before continuing the generation of the subpattern we first show two translations which are symmetry transformations of the generating Cm symmetry pattern. These two translations we will then use to generate the subpattern from the two elements already obtained (Figure 25).

Figure 26. Two translations (indicated by two vectors) are shown to be symmetry transformations of the generating Cm pattern. We will use these translations to generate the rest of the elements of the above isolated subpattern.
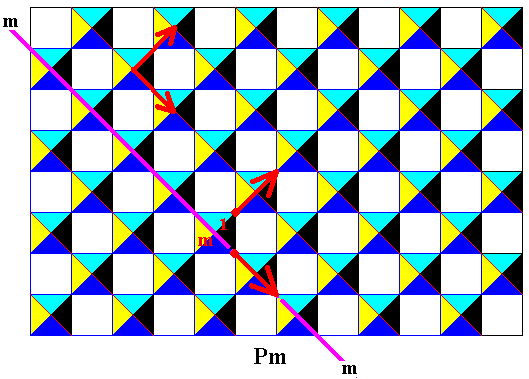
Figure 27. From the two elements (1 and m) obtained in Figure 25 we can generate the whole subpattern (i.e. the subpattern that was isolated from the above derived (alleged) antisymmetry pattern) by repeatedly applying to these elements the translations found in the previous Figure (In the present Figure indicated at several places by vectors).
Because the translations as well as the reflection used to generate the subpattern, are also symmetry transformations of the generating Cm symmetry pattern, the subpattern -- which has Pm symmetry -- is a subgroup of that generating pattern. It is, however, not a subgroup of the (alleged) antisymmetry pattern because its reflections are absent in the latter (Recall that all elements of a subgroup must also be elements of its coresponding full group). Therefore we will symbolize the above derived (alleged) antisymmetry pattern as Cm / *Pm.
In the next Figures we show the point lattice of the isolated subpattern, demonstrating that its symmetry is indeed according to the plane group Pm.
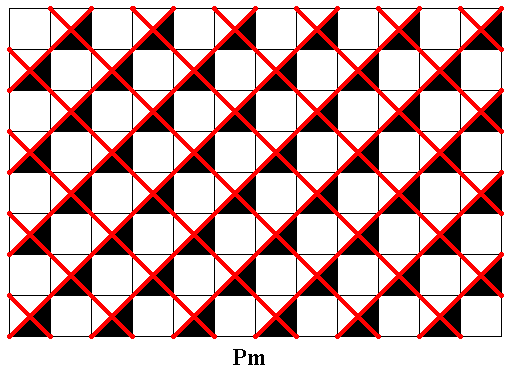
Figure 28. Point lattice (indicated by red connection lines) of the isolated subpattern of the (alleged) antisymmetry pattern consisting of the elements not affected by antisymmetry transformations. The lattice is a primitive rectangular net, with equivalent motifs at the corners of the net (and only at the corners of the net) (See next Figure).
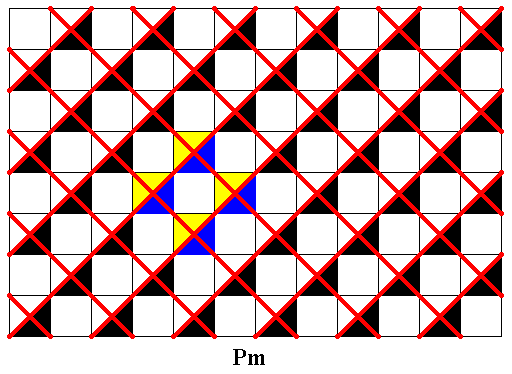
Figure 29. Same as previous Figure. Four equivalent motifs, associated with four lattice points, highligted, showing that the lattice is a primitive rectangular lattice. We further see that the motifs are symmetric in reflection lines of the pattern, and that there are also reflection lines of the pattern between the motifs. See Figure 24. All this demonstrates that the pattern has Pm symmetry.
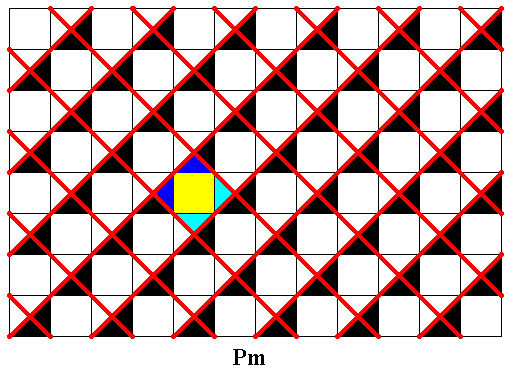
Figure 30. Same as in the two previous Figures. A unit mesh is indicated. Although the shape of the meshes is equal to a square, the lattice must be (primitive) rectangular (where a square is a spiecis of rectangle), because a genuine square lattice is not compatible with motifs having only D1 symmetry.
The next Figure shows the same pattern and the same point lattice as in the previous Figures, but now with that point lattice in a slightly different position with respect to the motifs.
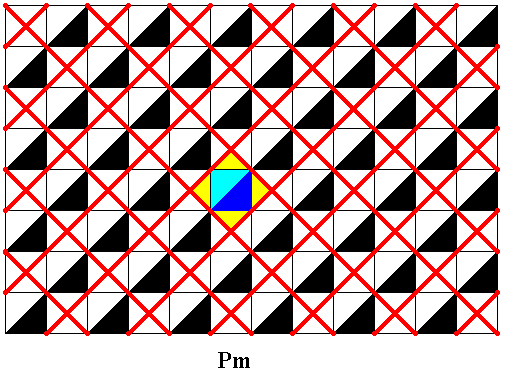
Figure 31. Same pattern as in previous Figure, but with the primitiv rectangular lattice slightly displaced. The two lattices are of course equally adequate to describe the periodicity of the pattern. A unit mesh is indicated.
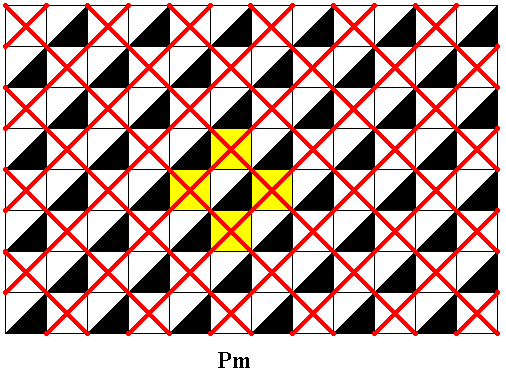
Figure 32. Same pattern (subpattern of alleged antisymmetry pattern) and lattice as in previous Figure. We can see that also this lattice is primitive.
As found out earlier the above derived 'antisymmetry pattern' is not an antisymmetry pattern at all. It misses reflections or their corresponding antisymmetry reflections, and thus cannot be derived by the transformations that are left : Two antisymmetry translations. And this means that the neolithic pattern cannot represent an antisymmetry group. It is just a symmetry group according to the plane group P1 .
Let's explain what we've just said.
If the neolithic pattern -- Figure 16 -- were representing an antisymmetry group derivable from the corresponding generating Cm symmetry group as represented in Figure 1 , then it must be possible to obtain it from that Cm group by replacing one or two elements of the latter by their corresponding antisymmetry transformations. The antiidentity transformation e1 must then change the solid black as we see it in the generating pattern into a striped pattern. Further the identity element must be the same in both the generating Cm pattern and the resulting antisymmetry pattern. And we know that the area representing a group element in the Cm pattern must have a triangular shape. It can be related to another such element by a reflection line (Recall that a group element is always represented by an asymmetric motif that is being repeated by the group transformations (symmetry transformations of the group) and in this way is forming the pattern that represents the group. So in generating the antisymmetry pattern we must start from the triangular area representing the identity element of the generating Cm pattern. See for this Figure 9 . A second element of the antisymmetry pattern to be derived must then be obtained by the horizontal antisymmetry translation e1t as in Figure 12 . Yet another element must be derived by the vertical antisymmetry translation in the same way :
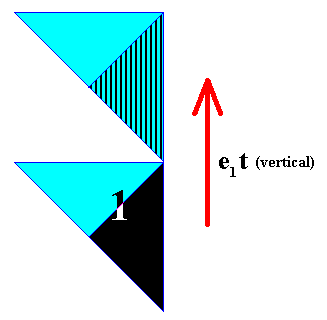
Figure 33. Generation of an element of the antisymmetry pattern by applying the vertical antisymmetry translation to the identity element.
Given these two antisymmetry translations we can now -- by repeatedly applying them -- generate the antisymmetry pattern :
Figure 34. Generation of an antisymmetry pattern according to the above specifications.
As one can see we have in fact generated only a part of the neolithic ornament (Figure 16 ) : We cannot generate the whole ornament, if we want it to represent an antisymmetry group derived from a Cm pattern (as JABLAN in Symmetry, Ornament and Modularity, 2002, claims (p. 144, Fig. 2.107)).
The next Figure indicates the point lattice of the just derived pattern (Figure 34).
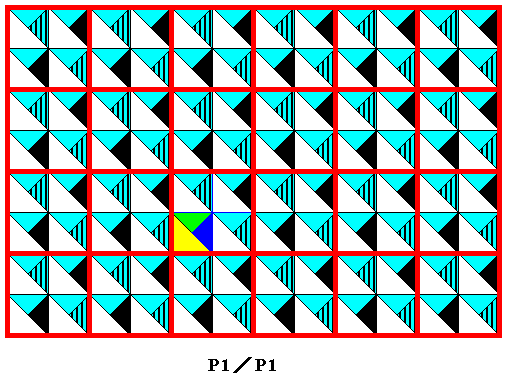
Figure 35. Point lattice (indicated by red connection lines) of the pattern (finally) generated in the previous Figure. We see that the pattern consists of an asymmetric motif that is repeated by two independent translations. As such it is a P1 pattern. Seen as representing an a n t i s y m m e t r y group it must be symbolized as P1 / P1 . The i d e n t i t y e l e m e n t of this antisymmetry pattern is indicated by alternative colors.
The next Figure gives an alternative point lattice of the just derived pattern. It is preferable, because its meshes are smaller.
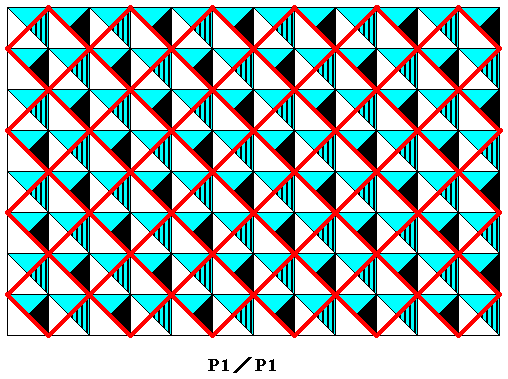
Figure 35a. Alternative and preferable point lattice (indicated by red connection lines) of the pattern (finally) generated in Figure 34 . Its meshes are smaller than those of the previous Figure.
If indeed we see the pattern just given as representing an antisymmetry group, then the generating symmetry group (i.e. the group from which the antisymmetry group is derived) can be represented by the following pattern :
Figure 36. Generating symmetry pattern, from which the pattern of Figure 34 can be derived as antisymmetry pattern, by replacing the two translations by their corresponding antisymmetry translations.
The next Figure indicates the point lattice of the generating symmetry pattern of the previous Figure.
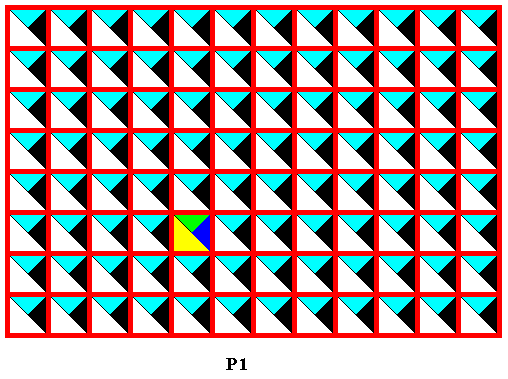
Figure 37. Point lattice (indicated by red connection lines) of the generating symmetry pattern, from which the pattern of Figure 34 can be derived as antisymmetry pattern, by replacing the two translations by their corresponding antisymmetry translations. The (chosen) identity element is indicated by alternative colors.
As we can deduce from the above Figure the generating pattern has a symmetry according to the plane group P1 , because the pattern consists of an asymmetric motif that is repeated by two independent translations.
The next Figure isolates from the antisymmetry pattern of Figure 34 all elements which are not the result of an antisymmetry transformation. One such element is, of course, the identity element.
Figure 38. Subpattern of the antisymmetry pattern of Figure 34 consisting of all elements that are not the result of an antisymmetry transformation.
The next Figure shows the point lattice of the subpattern of the previous Figure.

Figure 39. Point lattice (indicated by red connection lines) of the subpattern of the previous Figure.
The above Figure shows that the subpattern of the antisymmetry pattern of Figure 34 consists of an asymmetric motif that is repeated by two independent translations. So it is a group, and its symmetry is according to the plane group P1 . We will now investigate whether it is a subgroup of the generating pattern as well as of the antisymmetry pattern derived from it.
To begin with, we see two possible translations in our subpattern of Figure 38 :
Figure 40. Two possible translations (indicated by their vectors) of the s u b p a t t e r n of Figure 38 .
These same translations also occur in the antisymmetry pattern of Figure 34 :
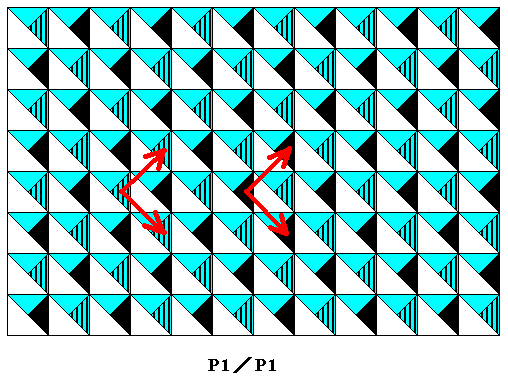
Figure 41. Two possible translations (one in NE direction, and one in SE direction, indicated by two local examples) of the antisymmetry pattern of Figure 34 . They are identical to those of the subpattern (Figure 38 ) that can be derived from it (See Figure 40 ).
And those same translations are also symmetry transformations of the generating symmetry pattern of Figure 36 :
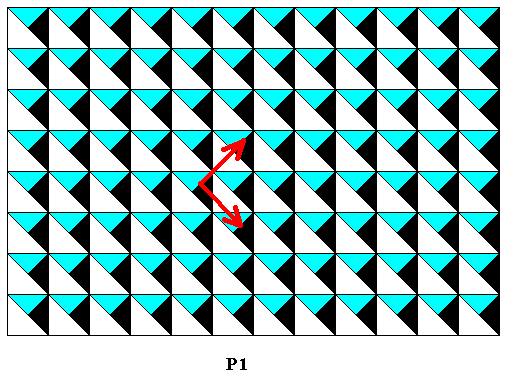
Figure 42. Two possible translations as symmetry transformations of the generating pattern of Figure 36 . They are identical to those of the antisymmetry pattern of Figure 34 as well as to those of the subpattern (Figure 38 , Figure 40 ) derived from the antisymmetry pattern.
So we now have established that the translations of the subpattern are also symmetry transformations of the antisymmetry pattern as well as of the generating pattern, and that the identity element is identically represented in all three patterns. This proves that the subpattern is a s u b g r o u p of the antisymmetry pattern as well as of the generating pattern. Consequently the symbol for the antisymmetry group that is represented by our antisymmetry pattern (Figure 34 ) is P1 / P1 (because the symmetry of the generating symmetry pattern is that of the plane group P1, while the symmetry of the subgroup involved in the antisymmetry is also that of P1).
This, finally, concludes our investigation of antisymmetry, subpatterns and subgroups in the plane group Cm , and of an alleged example of a Cm / Pm antisymmetry group in neolithic art.
In the next document we will investigate the plane group C2mm with respect to antisymmetry, subpatterns and subgroups.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology).
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV
Back to subpatterns and subgroups Part V
Back to subpatterns and subgroups Part VI
Back to subpatterns and subgroups Part VII
Back to subpatterns and subgroups Part VIII
Back to subpatterns and subgroups Part IX
Back to subpatterns and subgroups Part X
Back to subpatterns and subgroups Part XI
Back to subpatterns and subgroups Part XII
Back to subpatterns and subgroups Part XIII
Back to subpatterns and subgroups Part XIV
Back to subpatterns and subgroups Part XV
Back to subpatterns and subgroups Part XVI
Back to subpatterns and subgroups Part XVII
Back to subpatterns and subgroups Part XVIII
Back to subpatterns and subgroups Part XIX
Back to subpatterns and subgroups Part XX
Back to subpatterns and subgroups Part XXI