
e-mail :

Sequel to Group Theory
As always, we start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite two-dimensional periodic patterns, or Ornaments (sequel)
In the previous document we derived some antisymmetry patterns from an initial P2gg pattern.
The next antisymmetry pattern to be derived from the P2gg pattern of Figure 9 of the previous document can be obtained by replacing the horizontal glide reflection gh by the corresponding antisymmetry transformation e1gh , and the vertical generating translation tv by the corresponding antisymmetry transformation e1tv , where the antiidentity transformation e1 is again the color permutation (Red Blue) (cycle notation) with respect to the background color. We will derive the antisymmetry pattern in several steps. Newly generated red elements will initially be indicated by the color purple, and later be restored to red. Newly generated blue elements will initially be indicated by the color green and later be restored to blue.

Figure 1. The horizontal generating glide reflection (as the antisymmetry transformation e1gh) , applied to the identity element, creates a row of elements, lying on the corresponding glide line, with alternating colors.
In virtue of the generating vertical translation combined with the antiidentity transformation e1 (resulting in the antisymmetry transformation e1tv) being repeatedly applied to the identity element, the column of elements lying on the vertical glide line will contain a color alternation. Further, the element immediately above the identity element originates from the latter by (one time applying) the vertical generating glide reflection and therefore retains the blue color (indicated, for the time being, by green) of the identity element. If this new element is subjected to the vertical translation + e1 , new elements, alternating in color, will result, and the column will now show a two by two color alternation as indicated.
However, while the element immediately below the identity element (1) should indeed be red (as a change from the blue element immediately above the identity element), in virtue of the vertical translation + e1 ( = e1tv) , it should be blue, because it can be generated from the identity element by the vertical glide reflection, which does not involve a color change. But we must realize that the vertical glide reflection must -- with respect to color changes -- follow the generating antisymmetry translation e1tv , because gv2 = tv , where tv is replaced by e1tv , so gv2 = e1tv , and consequently repeatedly applying the symmetry transformation gv will involve color changes.
Above, speaking about the first stage of the derivation of the antisymmetry pattern, we stated "Further, the element immediately above the identity element originates from the latter by (one time applying) the vertical generating glide reflection and therefore retains the blue color (indicated, for the time being, by green) of the identity element." But it is obvious that we can, instead of doing this with the element directly above the identity element, do it with respect to the element directly below it. The result is depicted in the next Figure.
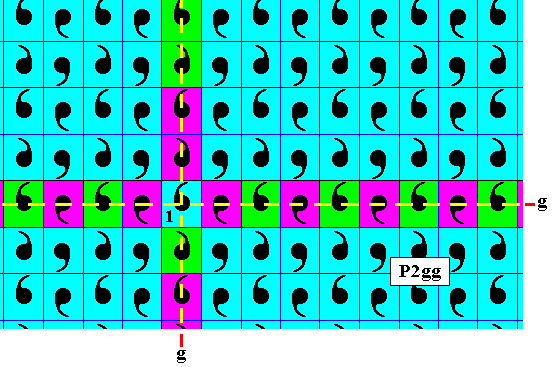
Figure 1a. Alternative possibility with respect to the elements above and below the identity element.
But because the upward and downward directions are equivalent in patterns with rectangular lattices, the antisymmetry pattern that would result from the above Figure (Figure 1a) will not be different from that derived from Figure 1 in any essential way.
Let us continue the derivation of the antisymmetry pattern (from Figure 1).
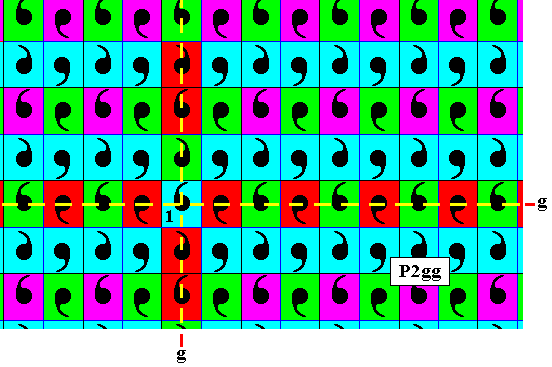
Figure 2. Applying the antisymmetry transformation e1tv repeatedly to the already generated elements, more elements, red (purple) as well as blue (green), will be generated.
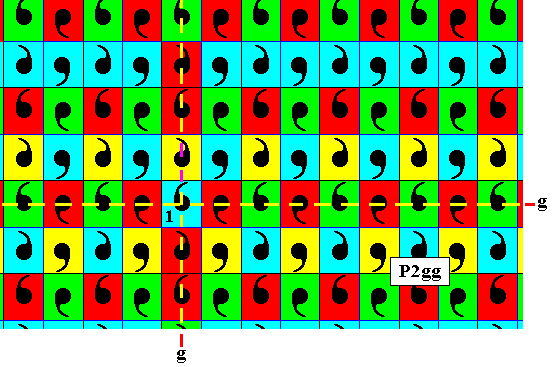
Figure 3. In this Figure we have marked some elements (yellow) that are involved in the horizontal generating glide reflection + e1 , i.e. in the antisymmetry transformation e1gh . The next Figure will show the effect of this transformation (which we can also denote as antisymmetry glide). The color of one of these involved elements was already established earlier : the element directly above the identity element (1), which is blue (initially indicated by green, and presently indicated by yellow).
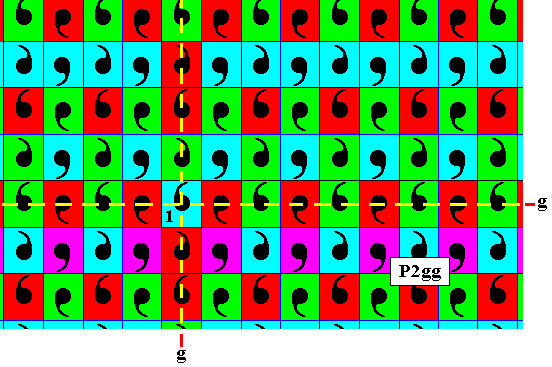
Figure 4. While the color of the element directly above the identity element was already established earlier -- namely as a result of subjecting the identity element (which it self is a blue element) to the vertical generating glide reflection, which leaves the color of this new element unchanged -- the color of the remaining elements involved in the transformation e1gh can now be assessed, as is done in the present Figure.

Figure 5. Applying the transformation e1tv to some already generated elements results in more red (purple) and blue (green) elements.
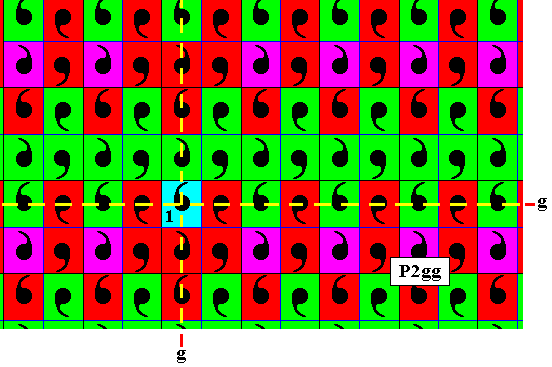
Figure 6. Applying the transformation e1tv to all the remaining generated elements results in more red (purple) and blue (green) elements, and completes the visible part of the pattern.
Restoring the green color to blue, and the purple color to red, results in the to be derived antisymmetry pattern :
Figure 7. Final stage of the derivation of the antisymmetry pattern from the generating P2gg pattern (Figure 9) by replacing the generating horizontal glide reflection by the corresponding antisymmetry glide reflection e1gh , and the generating vertical translation by the antisymmetry translation e1tv , where -- as always in the present investigation -- the antiidentity transformation e1 stands for the color permutation (Blue Red) (cycle notation) with respect to the background color.
The next Figure again depicts the just derived antisymmetry pattern, but now without indication of the symmetry elements (dashed lines) of the two generating glide reflections.
Figure 8. Antisymmetry pattern of the previous Figure.
Let us check whether this newly obtained pattern is indeed a true antisymmetry pattern, derived from the corresponding P2gg pattern by replacing the generating horizontal glide reflection gh by the corresponding antisymmetry glide reflection e1gh and at the same time replacing the vertical translation tv by the corresponding antisymmetry translation e1tv . These two antisymmetry transformations should effect a color alternation along their respective directions.

Figure 9. Starting from the identity element 1 , the antisymmetry transformation e1gh generates a row of elements lying on the glide line. The background color of the elements in this row indeed alternates between blue and red.
The elements that are highlighted by (temporarily) coloring the commas yellow, can be seen as being generated from element a by the same antisymmetry transformation e1gh , and their background color indeed alternates between red and blue.
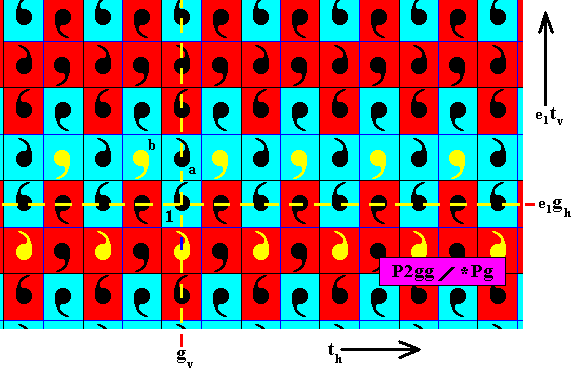
Figure 10. The elements that are highlighted by (temporarily) coloring the commas yellow, can be seen as being generated from element b by the same antisymmetry transformation e1gh , and their background color indeed alternates between red and blue.

Figure 11. The elements that are highlighted by (temporarily) coloring the commas yellow, can be seen as being generated from element c by the same antisymmetry transformation e1gh , and their background color indeed alternates between red and blue.
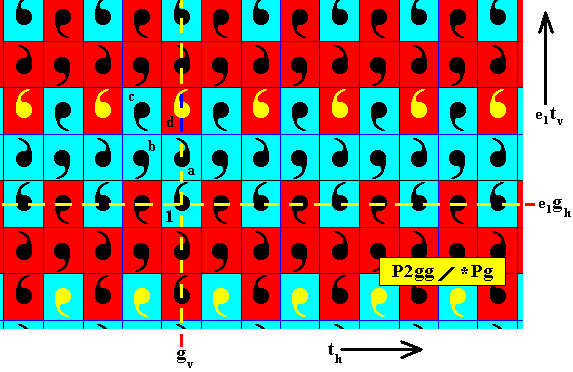
Figure 12. The elements that are highlighted by (temporarily) coloring the commas yellow, can be seen as being generated from element d by the same antisymmetry transformation e1gh , and their background color indeed alternates between red and blue.
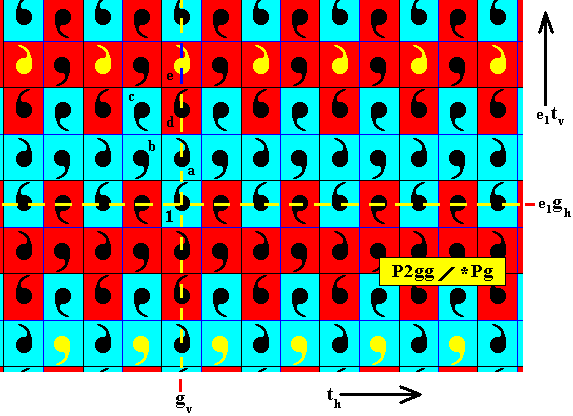
Figure 13. The elements that are highlighted by (temporarily) coloring the commas yellow (and extending the pattern downwards), can be seen as being generated from element e by the same antisymmetry transformation e1gh , and their background color indeed alternates between red and blue.

Figure 14. The elements that are highlighted by (temporarily) coloring the commas yellow (and extending the pattern downwards), can be seen as being generated from element f by the same antisymmetry transformation e1gh , and their background color indeed alternates between red and blue.
The above Figures have shown that the antisymmetry pattern indeed complies with the antisymmetry transformation e1gh .
The next Figure shows (by having the relevant commas temporarily colored yellow) that the antisymmetry pattern also complies with the antisymmetry transformation e1tv : The colors alternate.
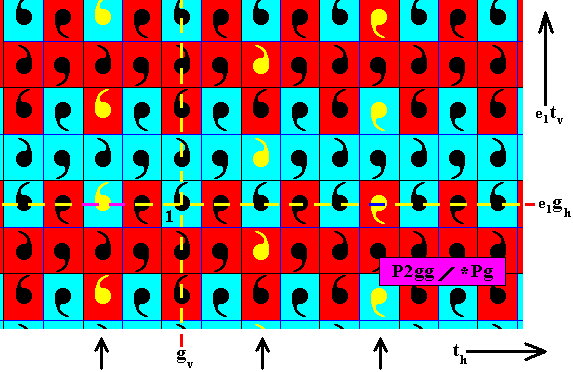
Figure 15. Three columns probed with respect to the antisymmetry transformation e1tv . The colors do indeed alternate.
The next two Figures show that the horizontal translation -- which is not an antisymmetry transformation -- does not involve an alternation of colors.
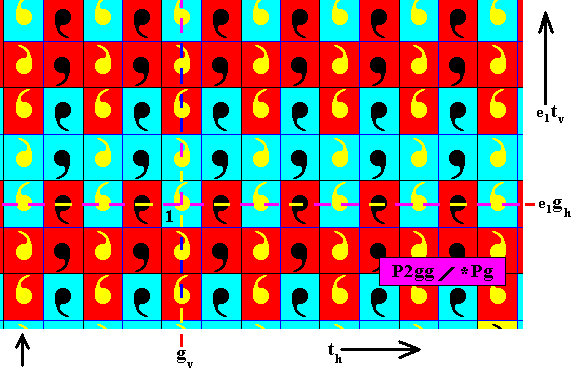
Figure 16. The rows of horizontally translated elements, according to the generator th , starting from the first column, show no color alternation.

Figure 17. The rows of horizontally translated elements, according to the generator th , starting from the second column, show no color alternation.
Now we concentrate on the transformation gv , i.e. the generating vertical glide reflection, which is not an antisymmetry transformation.
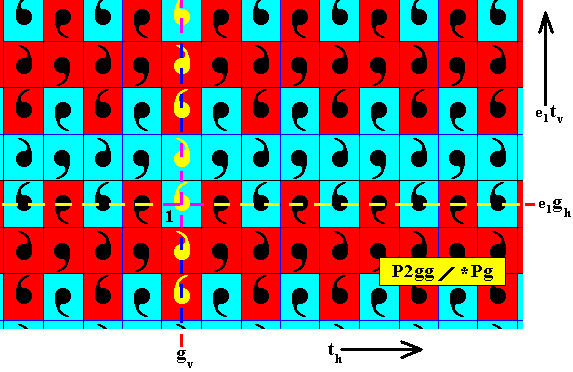
Figure 18. We can see that the configuration of the background color of the column containing the identity element, which (column) in itself represents the elements generated from the identity element by the generating vertical glide reflection, follows the antisymmetry transformation e1tv , i.e. in spite of the fact that the generating vertical glide reflection is not an antisymmetry transformation, it shows color changes. This is to be expected because gv2 = tv .
On the other hand, we saw in the Figures 16 and 17 that the generator th did not effect color changes, and this is in line with the fact that the antisymmetry generator e1gh gives color alternation, and thus automatically does not effect color alternation every two steps, i.e. it does not induce color alternation for th because gh2 = th .
We will now determine the symmetry of the subpattern involved in the just derived antisymmetry pattern in order to assess the latter's symbol. After that we will determine the point lattice underlying our antisymmetry pattern.
The next Figure isolates the blue elements of the above antisymmetry pattern.
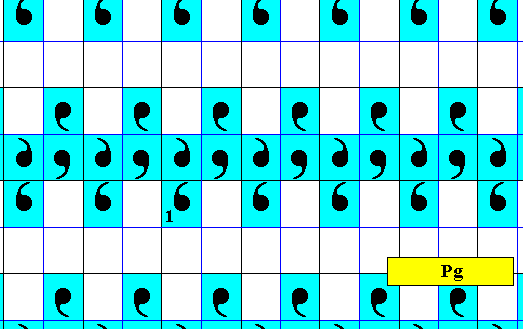
Figure 19 . Pattern consisting of the blue elements (including the identity element) of the pattern of Figure 8.
As the next Figures show, this pattern is indeed a periodic pattern, and has Pg symmetry. It is, however, not a s u b g r o u p of the pattern (Figure 8) from which it was derived.

Figure 20. The above pattern of blue elements (Figure 19) allows for a unit mesh to be indicated, proving that it is a p e r i o d i c pattern.

Figure 21. Point lattice of the above pattern of blue elements (Figure 19).

Figure 22. The above periodic pattern of blue elements (Figure 19) has, as its only symmetry elements (horizontal) glide lines (So its only symmetry transformations are the corresponding glide reflections and horizontal and vertical translations). So its symmetry must be according to the plane group Pg .
The next Figure shows why our subpattern of blue elements cannot be a subgroup of the antisymmetry group.
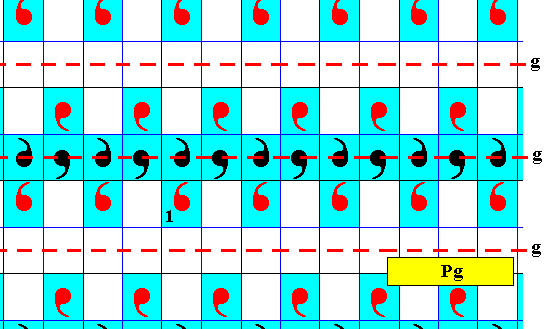
Figure 23. By means of the symmetry transformations of the antisymmetry group (and also of those of the generating P2gg symmetry group) not all elements of the pattern of blue elements can be reached starting from the identity element. The elements that can be reached are indicated (red). They can be reached by the horizontal glide reflections. So the pattern is not a subgroup (because all the elements of such a subgroup must be derivable from the identity element by symmetry transformations of the full group). The element directly above the identity element can only be reached by a vertical glide reflection which is an element of the full generating group. But when we repeatedly apply this glide reflection we get outside the pattern, so this transformation cannot belong to the alleged subgroup. In the same way the elements lying directly to the upper right and upper left of of the identity element can be reached by a half-turn of the identity element. But, as can be seen in the Figure, such half-turns are not elements of the alleged subgroup.
The above Figure shows that the g r o u p e l e m e n t s of our Pg subpattern must be differently conceived. In other words the fundamental region of the subpattern cannot be the same as that of the antisymmetry pattern (and of the generating P2gg pattern for that matter). Indeed if we extend the former fundamental region four times in the upward direction, we get a new fundamental region from which the whole subpattern can be generated by applying to that region the horizontal glide reflection and a vertical translation :
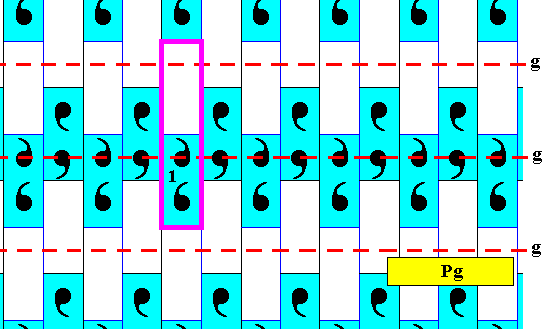
Figure 24. Areas representing group elements (any such area is a fundamental region) of the subpattern under discussion.
The next Figure shows how the horizontal glide reflection (glide line in the middle of the visible part of the pattern) multiplies the fundamental region (10 multiplications shown).
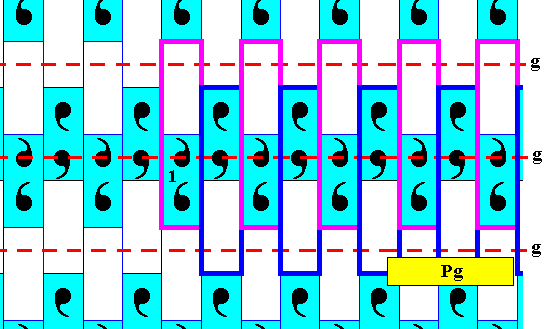
Figure 25. Multiplication of the fundamental region by the horizontal glide reflection of the subpattern under discussion.
If we vertically translate the result of the above multiplication in both directions we get the whole Pg subpattern. The next Figure shows the translation vector ( This vector is equal to tv2 of the generating P2gg symmetry pattern, while the same vector but now in the opposite direction is equal to tv-2 of the generating P2gg pattern [depicted in Figure 9 of the previous document] ).

Figure 26. Translation vector (red arrow), which (together with its inverse), when applied to the result of the above multiplication, completes the whole Pg subpattern.
So the above derived antisymmetry pattern (Figure 8) involves a subpattern with Pg symmetry. Because this subpattern does not represent a subgroup of the antisymmetry pattern (and also not of the generating P2gg symmetry pattern) we insert an asterisk (*) into the symbol of the antisymmetry group. This symbol is then : P2gg / *Pg .
The next Figures give the point lattice of the above derived antisymmetry pattern (Figure 7 ).

Figure 27. Point lattice (indicated by strong dark blue connection lines) of the above (Figure 7 ) derived antisymmetry pattern.

Figure 28. Unit mesh, indicated by yellow outline and alternative colors, for the antisymmetry pattern under discussion.
The next Figure, finally, gives -- for comparison -- the point lattice of the generating P2gg symmetry pattern from which the present antisymmetry pattern is derived.

Figure 29. Point lattice of the generating P2gg symmetry pattern.
In the next document we will investigate other antisymmetry patterns derivable from a P2gg pattern, and after discussing the subgroups of the latter, we continue with the other plane groups.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology).
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV
Back to subpatterns and subgroups Part V
Back to subpatterns and subgroups Part VI
Back to subpatterns and subgroups Part VII
Back to subpatterns and subgroups Part VIII
Back to subpatterns and subgroups Part IX
Back to subpatterns and subgroups Part X
Back to subpatterns and subgroups Part XI
Back to subpatterns and subgroups Part XII
Back to subpatterns and subgroups Part XIII
Back to subpatterns and subgroups Part XIV
Back to subpatterns and subgroups Part XV
Back to subpatterns and subgroups Part XVI
Back to subpatterns and subgroups Part XVII