
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite two-dimensional periodic patterns, or Ornaments (sequel)
In the previous document we considered the antisymmetry derivable from the plane group P2mm . Here we will look into some subgroups of that plane group not necessarily related to antisymmetry and color symmetry. After that we will continue our investigation into antisymmetry and subgroups of the remaining plane groups (ornaments).
Figure 1. A pattern representing the plane group P2mm .
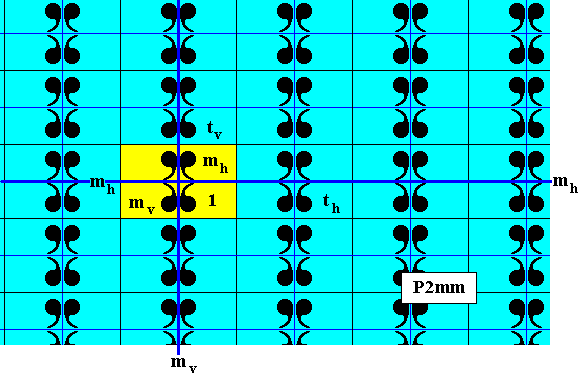
Figure 2. The subgroup D2 (yellow), (which is a point group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a horizontal reflection (i.e. reflection in a horzontal line) and a vertical reflection (i.e. a reflection in a vertical line).
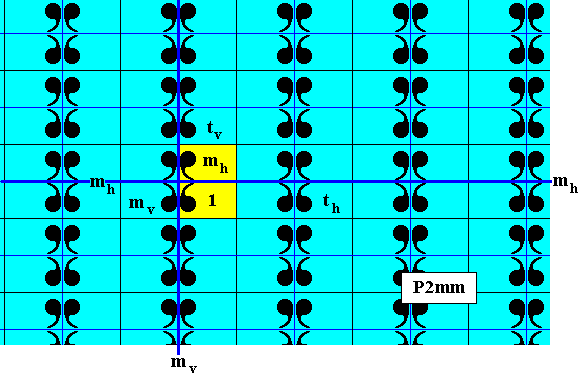
Figure 3. The subgroup D1 (yellow), (which is a point group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a horizontal reflection (i.e. reflection in a horizontal line).
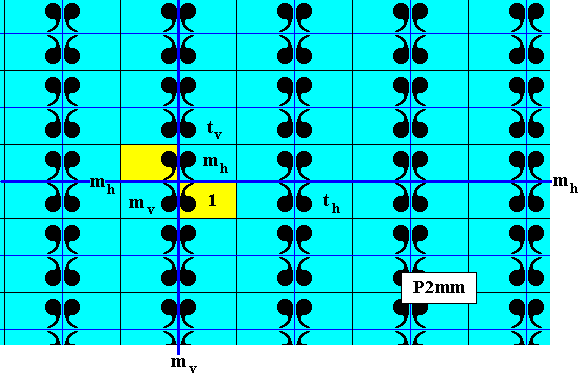
Figure 4. The subgroup C2 (yellow), (which is a point group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a half-turn.
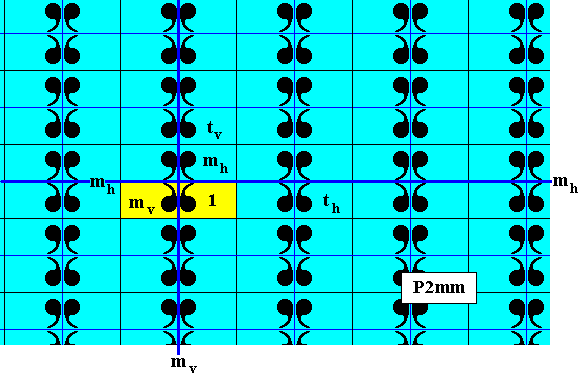
Figure 5. The subgroup D1 (yellow), (which is a point group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a vertical reflection (i.e. reflection in a vertical line).
The subgroups given above are finite groups, while the next subgroups are infinite groups.
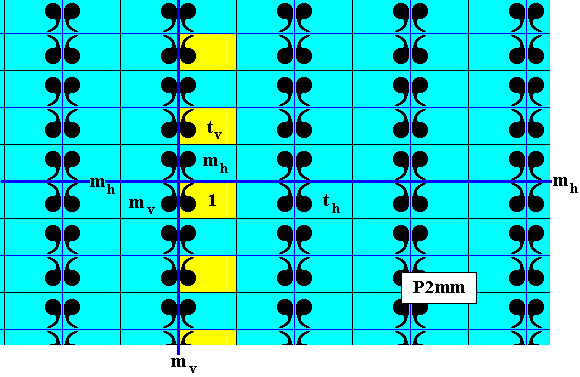
Figure 6. The subgroup p11 (yellow), (which is a line group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a vertical translation.
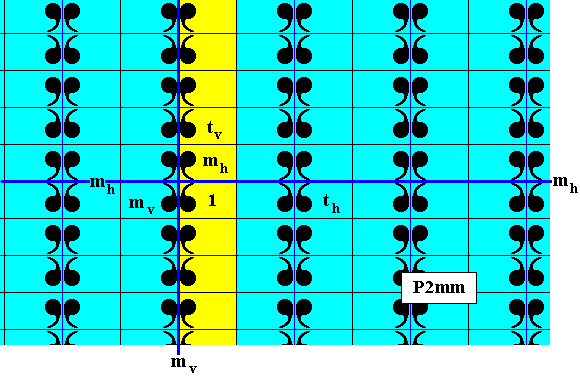
Figure 7. The subgroup pm1 (yellow), (which is a line group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a vertical translation and a horizontal reflection (i.e. a reflection in a horizontal line).

Figure 8. The subgroup pmm (yellow), (which is a line group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a vertical translation, a vertical reflection (i.e. reflection in a vertical line), and a horizontal reflection (i.e. reflection in a horizontal line).
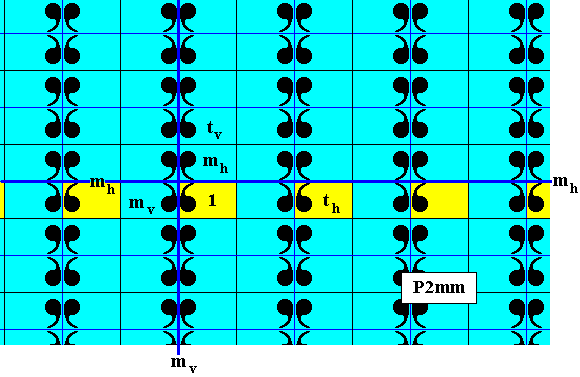
Figure 9. The subgroup p11 (yellow), (which is a line group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a horizontal translation.

Figure 10. The subgroup p1m (yellow), (which is a line group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a horizontal reflection (i.e. reflection in a horizontal line) and a horizontal translation.

Figure 11. The subgroup pmm (yellow), (which is a line group), of the plane group P2mm as represented by the pattern of Figure 1. The generator set of the subgroup consists of a horizontal reflection (i.e. reflection in a horizontal line), a vertical reflection (i.e. a reflection in a vertical line) and a horizontal translation.
This concludes our exposition of the plane group P2mm with respect to its subgroups (represented by subpatterns) and antisymmetry groups (represented by antisymmetry patterns).
We will now consider the plane group P2mg , where we investigate antisymmetry groups derivable from it, and subgroups not associated with antisymmetry (or color symmetry).
The next Figure gives a pattern representing this plane group.
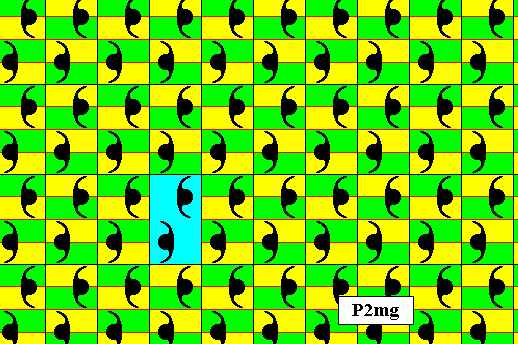
Figure 12. Pattern representing plane group P2mg . The motifs s.str. are (chosen to be) a set of four commas (two by two partly overlapping), and as such placed inside the lattice meshes. A quarter of a lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit of the motif s.str. . A lattice mesh is indicated (blue).
In order to derive an antisymmetry pattern from the pattern of Figure 12, an antisymmetry with respect to the background color, we set the latter -- as initial color -- as being the color blue.
Figure 13. The intitial background color of the above P2mg pattern is set to be blue.
The next Figure indicates the generating glide reflection and mirror reflection of the above P2mg pattern.

Figure 13a. Generating glide reflection (g) and mirror reflection (m) of the P2mg pattern of the previous Figures.
The first antisymmetry pattern will be derived by replacing the horizontal translation by its corresponding antisymmetry transformation, where the antiidentity transformation e1 is the color permutation ( Blue Red ) (cycle notation) with respect to the background color. The other generators will not be replaced. The next Figure gives the result.
Figure 14. Antisymmetry pattern ( P2mg / P2mg ) derived from the P2mg pattern of Figure 13 by replacing the generating horizontal translation by its corresponding antisymmetry transformation, where the antiidentity transformation e1 is the color permutation ( Blue Red ) (cycle notation) with respect to the background color.
The generating reflection is indicated by the (solid) blue line m . The identity element 1 is indicated.
The set of blue elements, containing the identity element, forms a subgroup P2mg of the full group (i.e. of the antisymmetry group as well as of the generating group). In this subgroup the horizontal generating translation is twice as long as the corresponding translation (th) of the generating group, so it, and the elements it generates (by its repetition), are also elements of that generating group. They are also elements of the present antisymmetry group, namely the elements . . . th-2 (= e1th-1e1th-1 ), , th2 (= e1the1th ), th4 (= (th2)2 ) . . . . Therefore the symbol for the antisymmetry group must be P2mg / P2mg .
Let us elaborate a little more on the symmetry of this subgroup.
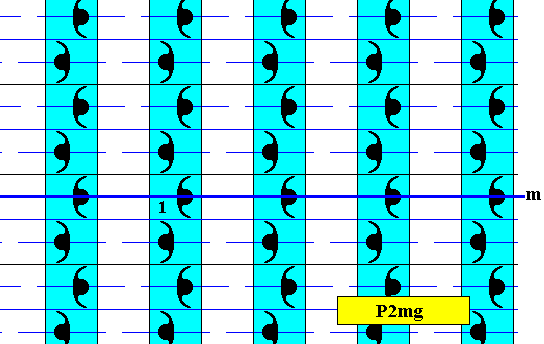
Figure 14-1. The subpattern of blue elements of the above derived antisymmetry pattern is isolated. The line m still represents a generating reflection of the subpattern.
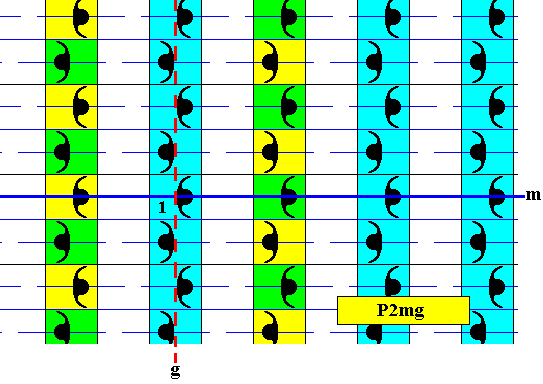
Figure 14_2. The subpattern of blue elements derived above.
It is shown that this subpattern still contains a generating (vertical) glide reflection (g) (and also a generating reflection as shown above). So the pattern must have P2mg symmetry.
And because (1) we can generate this subpattern from the area representing the identity element of the generating P2mg pattern (from which the antisymmetry pattern has been derived), namely (2) by applying to it the generating reflection m and (3) the generating glide reflection g -- which are both elements of the generating pattern (from which the antisymmetry pattern was derived) -- and, moreover, (4) the vertical translation of the subpattern being also a group element of the generating pattern, and (5) the horizontal translation of the subpattern being equal to two times the horizontal translation of the generating pattern, and therefore also being an element of the latter, this subpattern is a s u b g r o u p of that generating pattern. Compare with the (point lattice of the) generating pattern, depicted in Figure 14a.
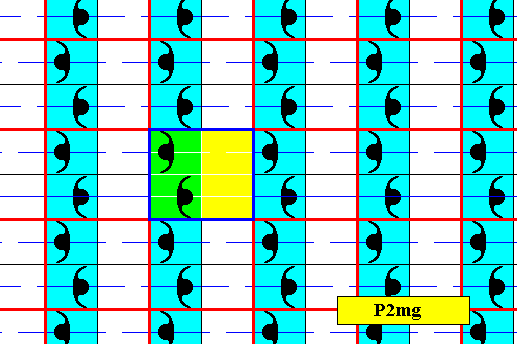
Figure 14_3. Point lattice (indicated by strong red connection lines) of the subpattern of blue elements derived above and representing a subgroup of the above derived antisymmetry group. A unit mesh is indicated by strong dark blue outline and alternative colors. Compare with the point lattice of the generating pattern, depicted in Figure 14a.
The next two Figures give the respective point lattices of the generating P2mg pattern of Figure 13 and of the just derived antisymmetry pattern of Figure 14.
Figure14a. Point lattice (indicated by strong dark blue connection lines) of the generating P2mg pattern of Figure 13. A unit mesh is indicated by yellow outline and alternative color (green).
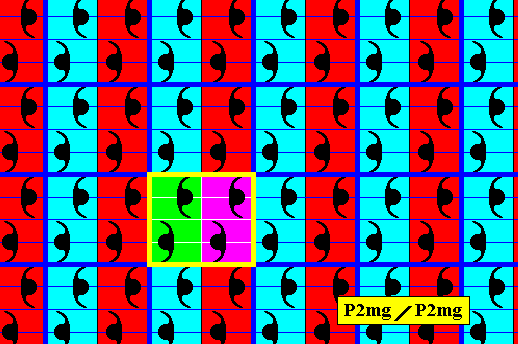
Figure 14b. Point lattice (indicated by strong dark blue connection lines) of the antisymmetry pattern of Figure 14. A unit mesh is indicated by yellow outline and alternative colors.
The next antisymmetry pattern can be derived from the P2mg pattern of Figure 13 by replacing the generating vertical glide reflection by the corresponding antisymmetry transformation. The next two Figures show the derivation.

Figure 15. First phase of the derivation of an antisymmetry pattern from the P2mg pattern of Figure 13 by replacing the generating glide reflection -- indicated by the dashed vertical line -- by its corresponding antisymmetry transformation, while letting the other generators unreplaced. In all cases where the generating glide reflection is applied an odd number of times, a color change will take place with respect to the initial background color of the area representing the identity element (1) , according to the color permutation (Blue Red) . Here we concentrated on the repeated glide reflection executed on the identity element. The horizontal translations applied to the new elements do not alter the color of these new elements, so a striped pattern is obtained.
The next Figure gives the completion of the derivation of the antisymmetry pattern.

Figure 16. Second and final phase of the derivation of the above defined antisymmetry pattern. We reflect the identity element in the reflection line m , which does not effect a color change, and then repeatedly apply the glide reflection in the vertical dashed line, effecting an alternation of colors. The other generating transformations do not effect color changes.
From the above Figure we can see that the set of blue elements (containing the identity element) forms the subgroup Pm . Therefore the symbol for the derived antisymmetry pattern must be P2mg / Pm .
The next Figure gives the point lattice of the just derived antisymmetry pattern.

Figure 16a. Point lattice (indicated by strong dark blue connection lines) of the antisymmetry pattern of Figure 16. A unit mesh is indicated by yellow outline and alternative colors. Compare with the point lattice of the generating P2mg pattern, (this lattice) depicted in Figure 14a.
The next antisymmetry pattern can be derived from the P2mg pattern of Figure 13 by replacing the generating vertical glide reflection by the corresponding antisymmetry transformation, and at the same time replacing the generating horizontal translation by its corresponding antisymmetry transformation. The result is shown in the next Figure.
Figure 17. Antisymmetry pattern P2mg / P2mg derived from the P2mg pattern of Figure 13 according to the above specifications. One other non-generator (implied) glide line (yellow dashed line) as a symmetry element of the original pattern is indicated.
The next Figure shows that the set of blue elements (containing the identity element) is a subgroup of the antisymmetry group, and this subgroup has P2mg structure. Therefore the symbol for this antisymmetry group -- as represented in the above Figure -- must be P2mg / P2mg .

Figure 18. The subgroup P2mg of the full group (the antisymmetry group P2mg / P2mg ) isolated. It has the identity element, and lacks some transformations of the full (antisymmetry) group -- for example the vertical glide reflection along the blue dashed line (of the previous Figures) combined with the color change -- whereby all the transformations it actually possesses are also transformations of the full (antisymmetry) group. The non-generator glide reflection (red dashed line) indicated in the previous Figure is still present (together with many others) as a symmetry element in the subgroup pattern. Compare the present Figure with Figure 13.
The next Figure gives the point lattice of the just derived antisymmetry pattern.
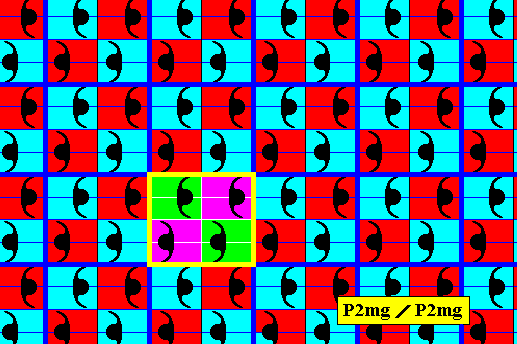
Figure 18a. Point lattice (indicated by strong dark blue connection lines) of the antisymmetry pattern of Figure 17. A unit mesh is indicated by yellow outline and alternative colors. Compare with the point lattice of the generating P2mg pattern, (this lattice) depicted in Figure 14a.
As one can check, it is impossible to derive an antisymmetry group from the symmetry group P2mg by replacing the generating (vertical) glide reflection and the generating vertical translation by their corresponding antisymmetry transformations. This is because the (vertical) glide reflection and the vertical translation are not independent generators : Two times such a glide reflection is identical to a vertical translation. And this implies that the two mentioned replacements end up in a contradiction : Two times the transformation e1g (where g is the mentioned glide reflection) will neutralize e1 and no color change will take place. But this transformation is equivalent to a vertical translation plus color change.
Yet another antisymmetry pattern can be derived from our initial P2mg pattern by replacing the generating reflection by its corresponding antisymmetry transformation, while letting the other generators unreplaced. The next Figure gives the result.
Figure 19. Antisymmetry pattern representing the antisymmetry group P2mg / Pg , derived from the P2mg pattern of Figure 13, by replacing the generating reflection by its corresponding antisymmetry transformation.
The set of blue elements in the antisymmetry pattern just derived (and containing the identity element) forms the subgroup Pg of the full group. Therefore the symbol for this antisymmetry group must read P2mg / Pg . The next Figure isolates this subgroup in order to highlight its structure.

Figure 20. Pattern representing the subgroup Pg of the above pattern representing the antisymmetry group P2mg / Pg .
The next Figure shows the point lattice of the above derived subpattern (being a subgroup of the just derived antisymmetry group).

Figure 20-1. Point lattice (indicated by strong red connection lines) of the pattern representing the subgroup Pg of the above pattern representing the antisymmetry group P2mg / Pg . A unit mesh is indicated by strong dark blue outline and alternative color ( The fact that we can indicate a point lattice proves that the structure is periodic).
The next Figure gives the point lattice of the just derived antisymmetry pattern.

Figure 20a. Point lattice (indicated by strong dark blue connection lines) of the antisymmetry pattern of Figure 19. A unit mesh is indicated by yellow outline and alternative colors. Compare with the point lattice of the generating P2mg pattern, (this lattice) depicted in Figure 14a.
Again, another antisymmetry pattern can be derived from our initial P2mg pattern by replacing the generating reflection and the generating horizontal translation by their corresponding antisymmetry transformations. See next Figure.
Figure 21. Antisymmetry pattern representing the antisymmetry group P2mg / P2gg , derived from the P2mg pattern of Figure 13, by replacing the generating reflection and the generating horizontal translation by their corresponding antisymmetry transformations.
The set of blue elements in the antisymmetry pattern just derived (and containing the identity element) forms the subgroup P2gg of the full group. Therefore the symbol for this antisymmetry group must read P2mg / P2gg . The next Figure isolates this subgroup in order to highlight its structure.
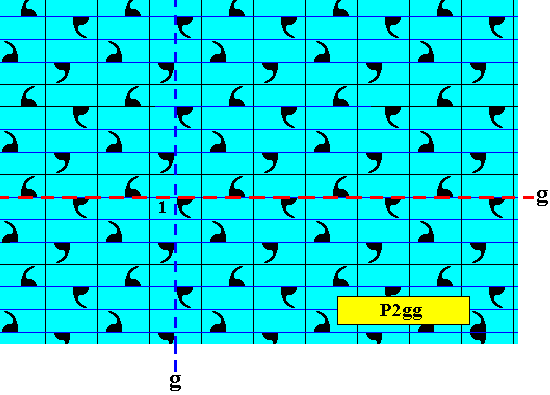
Figure 22. Pattern representing the subgroup P2gg of the above pattern representing the antisymmetry group P2mg / P2gg . Two glide lines are indicated (dashed lines). As one can see, the horizontal reflections are turned into glide reflections. This does not mean the appearance of a new group element (which would not be allowed if the group, as it is represented in the present Figure, is to be a subgroup of the full group), because a reflection always contains a glide reflection.
The point lattice of the just derived subpattern, representing a subgroup of the above derived antisymmetry group P2mg / P2gg as well as of the generating group P2mg , is given in the next Figure, demonstrating that the pattern is periodic.
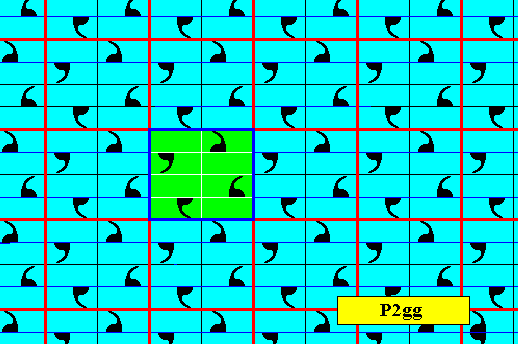
Figure 22_1. Point lattice (indicated by red connection lines) of the pattern representing the subgroup P2gg of the above pattern representing the antisymmetry group P2mg / P2gg . A unit mesh is indicated by strong dark blue outline and alternative color.
The next Figure gives the point lattice of the just derived antisymmetry pattern.

Figure 22a. Point lattice (indicated by strong dark blue connection lines) of the antisymmetry pattern of Figure 21. A unit mesh is indicated by yellow outline and alternative colors. Compare with the point lattice of the generating P2mg pattern, (this lattice) depicted in Figure 14a.
Finally, another antisymmetry pattern can be derived from our initial P2mg pattern by replacing the generating reflection and the generating (vertical) glide reflection by their corresponding antisymmetry transformations. See next Figure.
Figure 23. Antisymmetry pattern representing the antisymmetry group P2mg / P2 , derived from the P2mg pattern of Figure 13, by replacing the generating reflection and the generating (vertical) glide reflection by their corresponding antisymmetry transformations.
In the above Figure we can see that the set of blue elements (containing the identity element) is a subgroup of the full (antisymmetry) group, a subgroup with P2 symmetry. Therefore the symbol for the corresponding antisymmetry group must be P2mg / P2 . See next Figure which depicts this subgroup in isolation.

Figure 24. Pattern representing the subgroup P2 of the full (antisymmetry) group depicted in the previous Figure. Some of the 2-fold rotation axes (which are the symmetry elements of the pattern's half-turns) are indicated (small red solid ellipses).
The next Figure indicates the point lattice underlying the pattern of Figure 24. It shows the periodic repetition of motifs with C2 symmetry (resulting in a P2 pattern).

Figure 24a. Point lattice (indicated by purple connection lines) of the pattern representing the subgroup P2 of the full antisymmetry group (Figure 23).
The next Figure gives the point lattice of the just derived antisymmetry pattern.
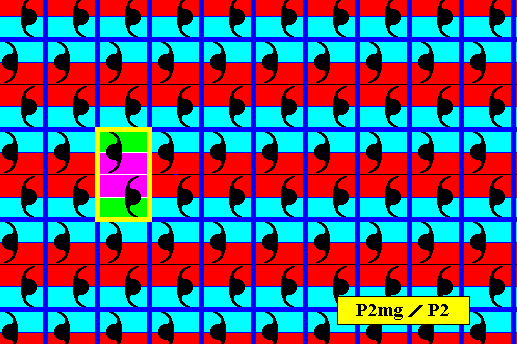
Figure 24b. Point lattice (indicated by strong dark blue connection lines) of the antisymmetry pattern of Figure 23. A unit mesh is indicated by yellow outline and alternative colors. Compare with the point lattice of the generating P2mg pattern, (this lattice) depicted in Figure 14a.
Subgroups
We will now discuss some of the possible subgroups of the group P2mg not necessarily associated with antisymmetry or color symmetry.
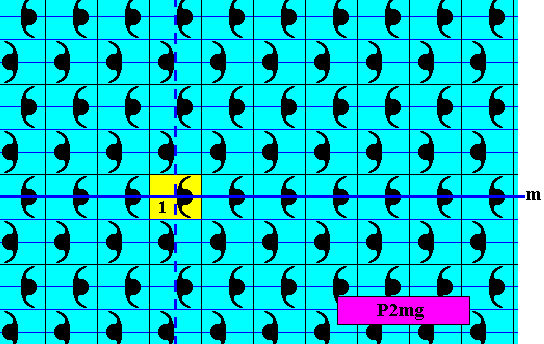
Figure 25. Pattern representing the subgroup D1 (yellow), which is a point group, of the full group P2mg depicted in Figure 13.
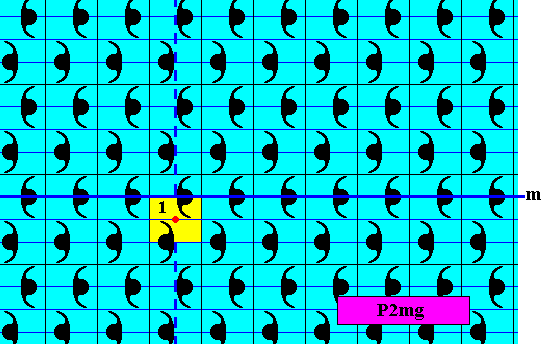
Figure 25a. Pattern representing the subgroup C2 (yellow), which is a point group, of the full group P2mg depicted in Figure 13. The axis of the generating half-turn is indicated by a red dot.
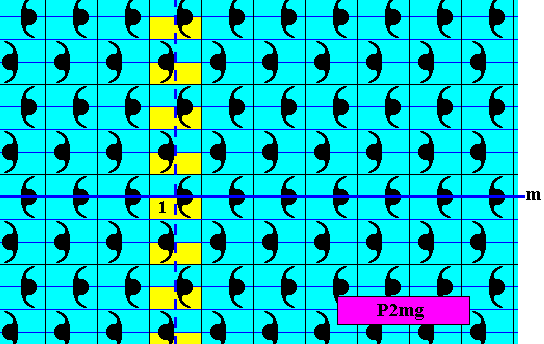
Figure 26. Pattern representing the subgroup p1g (yellow), which is a line group, of the full group P2mg depicted in Figure 13.
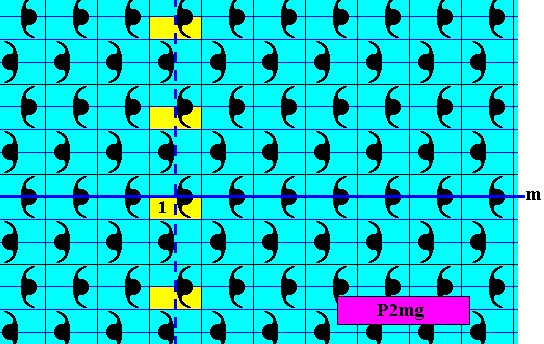
Figure 27. Pattern representing the subgroup p11 (yellow), which is a line group, of the full group P2mg depicted in Figure 13.
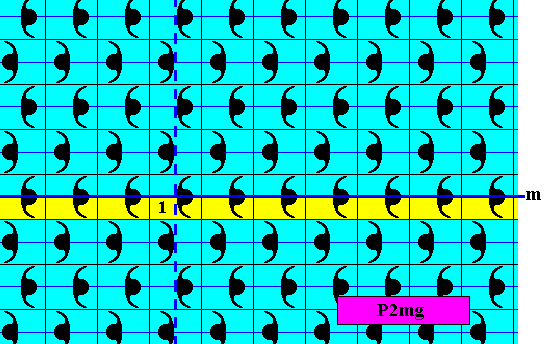
Figure 28. Pattern representing the subgroup p11 (yellow), which is a line group, of the full group P2mg depicted in Figure 13.

Figure 29. Pattern representing the subgroup p1m (yellow), which is a line group, of the full group P2mg depicted in Figure 13. The generator set of this subgroup is {m, th} , where m is the generating reflection in a horizontal line, and th the horizontal generating translation.
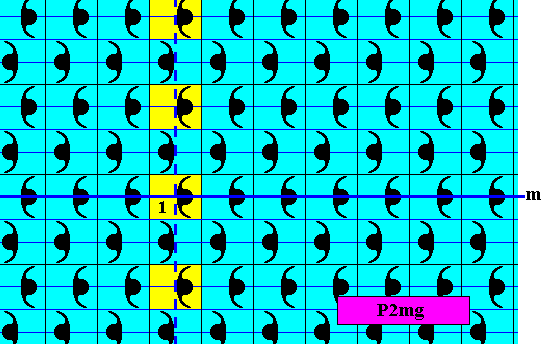
Figure 30. Pattern representing the subgroup pm1 (yellow), which is a line group, of the full group P2mg depicted in Figure 13. The generator set of this subgroup is {m, tv} , where m is the generating reflection in a horizontal line, and tv the vertical generating translation.
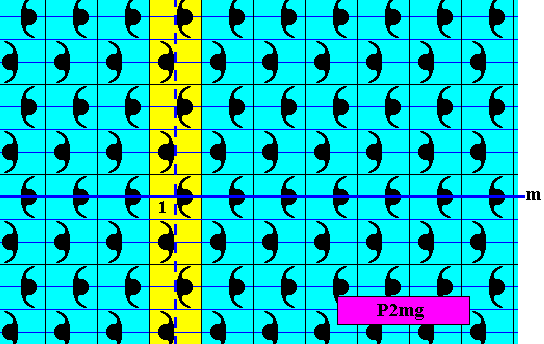
Figure 31. Pattern representing the subgroup pmg (yellow), which is a line group, of the full group P2mg depicted in Figure 13. The generator set of this subgroup is {m, g} , where m is the generating reflection in a horizontal line, and g the (vertical) generating glide reflection.
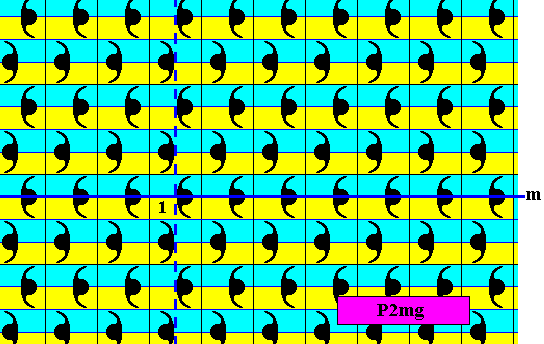
Figure 32. Pattern representing the subgroup Pg (yellow), which is a plane group, of the full group P2mg depicted in Figure 13. The generator set of this subgroup is {g, th} , where th is the generating horizontal translation, and g the (vertical) generating glide reflection.

Figure 33. The subgroup Pg of the previous Figure, which is a plane group, is isolated in order to highlight its symmetry.

Figure 34. The Figure indicates a unit mesh (unit cell) (blue) of the group Pg , depicted as a subgroup of the group P2mg in the previous Figure. Compare with Figure 1 of Part XIV ( There the glide line is horizontal, which in fact means that the pattern is rotated 900 with respect to the present pattern).
The next Figure indicates the point lattice underlying the pattern of Figure 34.
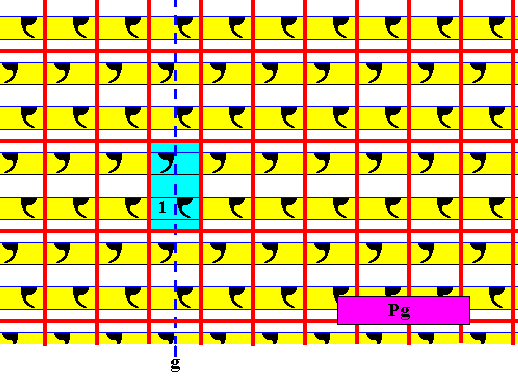
Figure 35. Point lattice (indicated by red connection lines) of the subgroup Pg of the (full group [P2mg] represented by the) pattern of Figure 32 (blue + yellow). Each motif consists of two motif units related to each other by a glide line.
The next Figure shows an alternative but equivalent position of the lattice with respect to the motifs.

Figure 36. Alternative, but equivalent position of the lattice (indicated by red connection lines) of the above pattern representing the group Pg .
This concludes our discussion of subgroups of the group P2mg , not necessarily associated with antisymmetry or color symmetry.
In the next document we will show some more examples of antisymmetry patterns derivable from P2mg patterns, among which as have been found in ancient ornamental art.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology).
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV
Back to subpatterns and subgroups Part V
Back to subpatterns and subgroups Part VI
Back to subpatterns and subgroups Part VII
Back to subpatterns and subgroups Part VIII
Back to subpatterns and subgroups Part IX
Back to subpatterns and subgroups Part X
Back to subpatterns and subgroups Part XI
Back to subpatterns and subgroups Part XII
Back to subpatterns and subgroups Part XIII
Back to subpatterns and subgroups Part XIV
Back to subpatterns and subgroups Part XV