e-mail : 

Sequel to Group Theory

Figure 1.  The subgroup  D₁  (which is isomorphic to  C₂ ). This subgroup is represented by a rosette consisting of two (areas that represent) group elements related to each other by a reflection.

Figure 2.  The subgroup  p1m  (which is a frieze pattern) of the group  Pm .

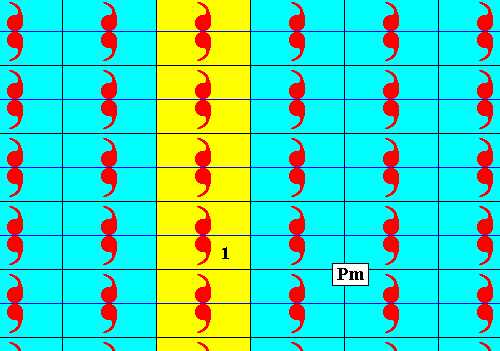
Figure 3.  The subgroup  pm1  (which is a frieze pattern) of the group  Pm .

In Part XII we discussed antisymmetry groups that can be derived from the symmetry group  Pm . Among those antisymmetry groups we found three different but isomorphic antisymmetry groups that, moreover, all had the same antisymmetry group symbol, namely  Pm / Pm . We will concentrate on two of them.
See Part XII for the symmetry group  Pm ,  Figure 1 .
A first antisymmetry group was derived from the symmetry group  Pm  by replacing the vertical translation by the corresponding antisymmetry transformation. The result was depicted in Figure 2 of Part XII.
A second antisymmetry group was derived from the symmetry group  Pm  by replacing the horizontal translation by the corresponding antisymmetry transformation. The result was depicted in Figure 3 of Part XII.
The symbol for both antisymmetry groups turned out to be  Pm / Pm .  But clearly they are -- despite their isomorphism -- different groups, because the group elements are different :  where we had, say, the element  e₁t_v  in the one group, we had the element  t_v  in the other. And the horizontal and vertical translations are not equivalent, because one is parallel to the pattern's reflection lines, while the other is perpendicular to them.
To distinguish between the two antisymmetry groups, we could denote the first one by the symbol  Pm / P1m  and the second one by the symbol  Pm / Pm1 . [By having a capital letter P, we distinguish the second part (signifying a plane group) of the antisymmetry symbol from the friezes (line groups)  p1m  and  pm1 ].

So we have here two groups, both  Pm / Pm ,  which are isomorphic to each other and isomorphic to the symmetry group  Pm .  The latter is nevertheless different with respect to the two antisymmetry groups. But the symmetry group  Pm  itself has the structure of the abstract group  D_infinite x C_infinite .  While in this latter group the what-is-it of the elements is exclusively determined by its group table (which in the present case is of infinite magnitude), the what-is-it of the group elements of the group  Pm  is further determined in virtue of their being interpreted as certain symmetry transformations, in the present case two translations (vertical and horizontal),  t_v  and  t_h ,  and a reflection  m  in a certain line.
And in the two antisymmetry groups  Pm / Pm  they are interpreted as the antisymmetry transformation  e₁t_v ,  the horizontal translation  t_h  and the reflection  m  for the one antisymmetry group, and interpreted as the vertical translation  t_v ,  the antisymmetry transformation  e₁t_h  and the reflection  m  for the other.
So we have here to do with one abstract group  D_infinite x C_infinite ,  in which the group elements are not interpreted, and three symmetry groups (in fact one symmetry group and two antisymmetry groups) where the group elements are interpreted as symmetry transformations or antisymmetry transformations.
And because our website is ultimately concerned with the ontological constitution of intrinsic things we ask ourselves how we should evaluate the ontological meaning and significance of the fact that we have to do with (1) uninterpreted abstract groups, which are just certain self-contained algebraic structures, and (2) with symmetry groups possessing that same algebraic structure, but in which the group elements are interpreted as symmetry or antisymmetry transformations in such a way that those interpretations are fully compatible to the algebraic structure of the abstract group.
The ontology of intrinsic things in general, is extensively discussed in the First Part of the Website, which is accessible by the BACK TO HOMEPAGE link at the end of the present document.
Recall that Ontology is about the metaphysical constitution of (intrinsic) things, which means that one is looking not for actual material parts that constitute such a thing (this is what Natural Science does), but to 'constituents' that determine the what-is-it of such a thing and of its properties (which is what Metaphysics does). While the central what-is-it of the intrinsic thing is the dynamical law of the dynamical system that generated that thing, and is discussed in the First Part of Website, the what-is-it of the symmetry of such an object (which is a property of that thing (object), and an important aspect of the thing's structure), is the main theme of the present Part of Website (Second Part of Website). And in a preliminary way we had already established that the symmetry group is the what-is-it of the symmetry of some given object. With the detection of abstract groups and their several possible interpretations as symmetry groups and antisymmetry groups, we must further work out the what-is-it issues with respect to symmetry and structure.
We will do so by taking some elementary abstract group (We chose the abstract two-element group), discussing its possible interpretations resulting in symmetry groups, and -- going down one more step along the line of increasing specification -- their corresponding promorphs, i.e. their corresponding stereometric basic forms ( The Theory of Stereometric Basic Forms is presented in this Second Part of Website, after the Series on three-dimensional Crystals, which itself comes after the present Series on Group Theory [One can, for a total overview of the whole website, consult the COMPLETE TABLE OF CONTENTS by clicking on the relevant LINK at the top of the left frame, or at the CONTENTS given on the HOMEPAGE ] ).

After the discussion of abstract group, symmetry group and promorph as ontological levels of a given intrinsic object, we discuss the general question of the ontological status of mathematical structures (like groups, or like the mathematical content of physical laws, etc.). So there we discuss the way of being of such structures, and the question of their possible independent existence.

The problem of the ontological status of mathematical structures and objects is a hard one, but very interesting in trying to solve it.
In order to consistently and successfully carry out such an investigation, I am presently exchanging ideas with Professor Jarbas Maciel from Recife, Brazil. He is very well at home in this problem, as well as in Mathematics, Logic, Ontology and Epistemology. He is enthousiastic about the investigations carried out so far on my website and told me that his investigations coincide remarkably with those of mine, and would like to communicate with me about the relevant issues. So I seize the opportunity for letting him comment and critisize the ideas I put forward with respect to the ontology of mathematical structures, because my acquaintance with Mathematics, Logic and Epistemology is more or less limited.
I have sent him the discussion, as given below in the present document, and asked for his comments.
Both of us are acquinted with the German philosopher Nicolai HARTMANN (having worked in the 20's 30's and 40's of the 20st century), who wrote much about General Ontology (The theory of Being qua Being) and Special Ontology (The theory of Categories or fundamental principles of Being).
HARTMANN adressed the problem of the ontological status of mathematical structures, and has set out to demonstrate their independent existence (i.e. independent of our thinking about them), an existence within -- what he calls -- the Ideal Sphere of Being, which distinguishes itself from the Real Sphere of Being by the non-individuality and general nature of its inhabitants, while in the Real Sphere all entities are individual. The difference between the two Spheres is thus a difference in the way of being-there of their respective inhabitants.
It is perhaps instructive to reproduce here the letter that accompanies the mentioned discussion sent by me to Professor Jarbas Maciel (October, 2003), because it is a fine introduction and overview of that discussion. It moreover contains some notes about my anti-dualistic position (and, consequently, monistic position) with respect to the mind-body problem, which position is important for any consideration concerning the ontological status of mathematical objects. After that letter the discussion itself will follow immediately.

Jaap

Although above I have indicated the philosophical context of my studies about symmetry, it is perhaps convenient to further elaborate on this context before we actually embark on the specific ontological discussion concerning mathematical structures.
In the First Part of my website we (the reader and I, so to say) have considered Ontology in the sense of the metaphysics of real individual material objects. This means that we discussed principles of Being, not in their complete generality, but as seen from an arbitrary (i.e. one or another given) individual material object or thing, 'seen', as it were, by the object itself in some ontological 'self-contemplation'. So the individual real object as such was the center of the ontological discussion. We have found out that such an object can only be considered to represent one genuine being if, and insofar as, it is produced by one dynamical system (physical or chemical). And we have further argued that the dynamical law of such a system, together with inital conditions (only insofar as they imply the dynamical law to be a physically interpreted mathematical law), is the Essence (in the metaphysical sense) of the generated object as a whole. This Essence is then considered to be an ontological component -- not a material part -- of that given object. It constitutes at the same time the intrinsic what-is-it of that object, and is its ontological core. The properties of the object are the visible results of the generation of that object. Those visible features are structure, composition, behavior, etc. They form the object's ontological periphery.
In the Second Part of website we have concentrated on STRUCTURE, i.e. on the structure of generated beings or things (like crystals and organisms). One of the main determinants of structure is SYMMETRY, and it is especially the latter to which our attention was directed, and still continues to do so. This symmetry is geometrically treated in our Promorphological System of the Ideal Stereometric Basic Forms of organisms, and was later extended to those of crystals (Second Part of website). Preceding all this, we have treated symmetry in an algebraic manner, by introducing Group Theory, with, of course, special emphasis on symmetry groups. So generally we are in the process of analysing symmetry as such, geared to an understanding of the symmetry of natural objects produced by certain dynamical systems. As has been said, symmetry is one of the visible features produced by the physically interpreted dynamical law of such a system. Such a symmetry can exhaustively be described by a symmetry group, which is moreover established to be the (algebraic) what-is-it of that given symmetry. This what-is-it is thus one or another mathematical structure provided with a certain interpretation, i.e. a certain interpretation of the group elements. This interpretation can be purely geometrical, and as such the what-is-it remains purely mathematical, but it can also be such that in one way or another the real material world is involved in the interpretation. It then is a physical interpretation of the group elements.
Now we ask ourselves what the ontological status is of a symmetry group so conceived, and also what the ontological status is of the corresponding abstract group (in which the group elements are not interpreted at all). And this automatically leads us on to the general question as to the ontological status of any mathematical structure whatsoever, be it a group, a function, an equation or mathematical law, a topological space or any other such structure. And we want to know how all kinds of ontological entities 'interact' to compose a genuine being or thing. All this will form the content of the discussion to follow.

Earlier ( Part V ) I have stated that a symmetry group describing the symmetry of a given (material) object IS the very symmetry of that object, i.e. it is not only a description but a genuine what-is-it of an aspect of the structure of that given object.
But, in fact the symmetry group is first of all very abstract, in such a way that it is indifferent to any real object or class of real objects. Let me explain that by means of specific examples represented by the next Figures.

Figure 4.  Abstract two-element group. It is represented by a group table. The two group elements  a  and  b  are placed alongside the vertical and horizontal lines. The possible combinations of these two group elements are given in the interior of the table, in this way defining the (binary) group operation.

    aa = a
    ab = b
    ba = b
    bb = a

From these relations, following from the group table, we can see that the element  a  does not have any effect when it is combined either with itself or with the other element of the group, and so this element (the element  a) is the identity element. And although  aa = a ,  the relation  a = a  also holds, so the period of  a  (the identity element) is  1  (The period of a group element is equal to the lowest number of repeats of this element resulting in the identity element).
And because  bb = a ,   i.e.  b²  is equal to the identity element (while  b¹  is not), the period of  b  is  2 .  We call such an element involute.

So this group is totally indifferent with respect to any object in the real world, i.e. it is indifferent as to its possible realizations.
It can, however, be more closely determined in several ways, as soon as we interpret the elements in a specific way, compatible with the group table. See next Figure.

Figure 5.  Three 'realizations' of the abstract 2-element group as given above.

First, all three symbols must refer to symmetry transformations of some object, which means that the object, subjected to such transformations, remains the same in appearance, i.e. that the object occupies the same patch of space as it did before it was so subjected. Given this, the more specific interpretation will then be :

 m   is a reflection.
 i   is a central inversion (i.e. interchanging of opposite points).
 2   is a half-turn (i.e. a rotation by 180⁰).

Under these interpretations we now respectively have the groups  D₁ ,  C_i  and  C₂ .  And they are (now) symmetry groups.
Because the elements of all three behave according to the group table of Figure 4, these three symmetry groups are isomorphic to each other as well as to the abstract group, i.e. their algebraic structure is identical. So purely group theoretically they are indistinguishable.

It is evident that the above interpretation of the group elements as certain symmetry transformations presupposes some object having these symmetries, i.e. some object to which these transformations are applicable. So although the three symmetry groups  D₁ ,  C_i  and  C₂  are still in some degree abstract, they presuppose some given object, and when moreover, this object is a real material object, they mediate between the abstract group and the symmetry properties of that real object. In fact we could say that the abstract group on the one hand, and one (or another) of the three symmetry groups on the other, are two ontological layers within that object. In any case they relate to each other as genus to species (or as supergenus to genus for that matter)   [ When that given object is still an abstract object, such as a purely geometric figure, or any other purely mathematical object, the corresponding symmetry group is still a purely mathematical structure].

In addition to the above given interpretations of the non-identity element  b  of the abstract 2-group, as symmetry transformations, there are other possible, and for our case -- the structure of material objects -- relevant interpretations, namely the interpretation of the element  b  as the corresponding antisymmetry transformations   e₁m,   e₁i,  and  e₁2 ,  where the antiidentity transformation  e₁  is the color permutation  (White Black) (cycle notation), and for which the following holds :  e₁² = 1 (identity element), and  e₁S = Se₁, where  S  is any symmetry transformation of the group (The groups in our cases have only one symmetry transformation). This type of interpretation of the non-identity element of the abstract 2-element group results respectively in the antisymmetry groups  D₁ / C₁ ,   C_i / C₁  and  C₂ / C₁ ,  where the first part of the antisymmetry group symbol refers to the generating symmetry group, while the second part refers to the subgroup involved in the antisymmetry. These antisymmetry groups are all isomorphic to the abstract 2-element group. While in the above, the interpretation of the antiidentity transformation  e₁  was in terms of a color permutation between two colors, it can be in terms of any dual quality, like positive charge/negative charge, closed/open, etc.
As an example :  If we represent the symmetry group  D₁  by half a rhombic pyramid (isosceles pyramid), then the corresponding antisymmetry pattern -- where the antiidentity transformation  e₁  is set to be the black-white color permutation -- is again that same half a rhombic pyramid, but with one half being white and the other black (separated by the pyramid's median plane). The existing reflectional symmetry is now lost, and replaced by an alternation of colors.
Although antisymmetry groups are important for, and relevant to, the analysis of material structure, we will -- in this ontological intermezzo -- not pursue them further.

We can even add a third layer, which is, although less abstract, not yet fully concrete, namely one (or another) of the several different  promorphs  to which the above three symmetry groups each for themselves apply :  In the Series of documents (Second Part of Website) about the Promorphological System of Basic Forms I have established that the promorph of an object is the simplest geometric solid fully expressing the (point) symmetry of that object and, in addition to it, (expressing) the number and arrangement of the object's antimers (counterparts). It is the ideal stereometric basic form of that object, where "form" here refers to the external (idealized) shape of the object and its overall structure, i.e. its internal shape. In this way I have --- following Haeckel's Promorphology (1866) -- established all the geometric solids (cylinders, cones, bicones, pyramids, bipyramids, half-pyramids, etc.) that represent the (idealized) underlying symmetries of organismic bodies and also of their parts. However, I have extended this system also to crystals. Of course the (point) symmetries of crystals are already described in Crystallography in the form of the 32 Crystal Classes (point groups). Many symmetries and asymmetries in crystals, however, do not present themselves geometrically. Asymmetries often appear in the form of differently oriented striations on certain crystal faces of the same crystal, or in the form of chemical and physical differences between some faces of a crystal. In Promorphology I want to express these asymmetries (as well as symmetries) by the shapes of certain geometric solids. In this way I have set up a Promorphology of Crystals (In the last Series of Documents of the Second Part of Website). So there, all the 32 symmetry classes are represented by the simplest appropriate geometric solids expressing those symmetries fully, and so expressing the promorphs of those crystals (taken to have grown in a homogeneous medium free from disturbing effects). As will be clear from all this, the promorph (organic or inorganic) is a geometrically morphological interpretation of the group elements of a symmetry group (Further down we will work this out in more detail).
And in this way we can represent the three above discussed symmetry groups by corresponding promorphs, which are of course still in some degree abstract -- because still abstracting from non-promorphological features -- but are very close to actual forms.
As a rule, each symmetry group can be represented by several different promorphs. That's why each of them also corresponds to a certain general promorph.
Let us first summarize, and then discuss these general promorphs. First that of the symmetry group  C₂ ,  then that of the symmetry group  D₁  and finally that of the symmetry group  C_i  (click on the names of the promorphs, to see a representative).

The general promorph of intrinsic real objects with symmetry group  D₁  is  half a rhombic pyramid.  It belongs to the Zygopleura eudipleura (Stauraxonia heteropola heterostaura allopola) of the Promorphological System. In fact the general promorph is just half an amphitect pyramid, as such belonging to the Heterostaura allopola. In a drawing we represent it most conveniently by half a rhombic pyramid, in turn representing the Zygopleura eudipleura as a species of the Heterostaura allopola ( For the classification of the latter as given further below, click HERE ). See explanation and Figures below.

The promorph of intrinsic real objects with symmetry group  C_i  is a  triclinic bipyramid .  It belongs to the Anaxonia centrostigma, i.e. bodies having no (promorphological) axes but which do have a body center. Although this promorph can also be seen as 'general', it is at the same time also specific, because the physical bodies it represents, do not have antimers (bodily counterparts), and so do not admit of any further differentiation of this promorph. See explanation and Figures below.

For  O r g a n i s m s  we have erected a Form System that is fully inspired by the shapes (i.e. outer forms) and structure (i.e. inner form) of existing organisms. Their structure is  t e c t o l o g i c a l,   i.e. consisting of definite macroscopical parts that are repeated non-periodically. Every  b a s i c  f o r m  of an organismic individual and also of their subordinate individuals (cells, organs, antimers, etc.) is represented by a geometrical solid displaying the symmetry of that organismic individual.
C r y s t a l s  on the other hand, have a   p e r i o d i c   structure :   A certain microscopic unit is repeated periodically in three different spatial directions, which means that microscopic translations are involved in the crystal structure. So (single) crystals do not have macroscopical parts that are repeated non-periodically (while certain twinned crystals do), which means that they, in particular, do not possess  a n t i m e r s,   so important and determining with respect to the assessment of the stereometric basic form (promorph).
But when we conceptually eliminate all translations inherent in crystals, i.e. eliminate all translational symmetry -- which in turn means that we eliminate (1) simple translations, (2) the translational component of every glide plane, and (3) the translational component of every screw axis -- then we are left with just one  c h e m i c a l  m o t i f,   formed by the superposition of motifs in the lattice. I.e. when we 'telescope' the crystal back, we end up with the  p o i n t  s y m m e t r y  only, represented by the (one) mentioned chemical motif. Consequently, this motif is the result of the superposition of all the point environments of the lattice. Such an environment consists of the whole set of chemical elements (in the sense of parts or particles) associated with a lattice point. Because of the superposition of the lattice points (by means of eliminating all simple translations), we are left with one such an environment. But in addition to simple translations there can be the translational elements of glide planes and screw axes. Also these translations should be eliminated. This can result in the mentioned environment to be telescoped further back, resulting in a smaller motif. This finally resulting motif corresponds either with one formula unit of the substance involved, or with a multiple thereof. In Ice this finally resulting motif consists (as far as my knowledge goes) of one hexagonal ring of six water molecules. Well, this final motif indeed has a   t e c t o l o g i c a l   structure, and because of this the crystal can be promorphologically assessed after all. How do we do this? (This is explained in the mentioned Series of documents).

Below, the results (concerning the determination of the promorph) are given for crystals of the three Crystal Classes having the above considered symmetry groups 
C₂  (in the crystallographic literature given as  2 ),
D₁  (in the crystallographic literature given as  m ), and
C_i  (in the crystallographic literature given as a  1  with above it a score).

If one clicks on the names of these promorphs (as given below), the one relevant document -- as one of the documents that make up the Promorphological System -- will appear in a separate window. One can then see some context in which the given promorph resides by looking up the promorph in that document. After consulting, one should close the window in order to return to the present document. If one wants to consult the whole set of documents concerning the Promorphological System, one should return (click) to the beginning of the Second Part of Website, and then go to the Series on Basic Forms (Promorphological System).

In fact the general promorph for all the crystals of this Class is just that of the Heterogyrostaura (amphitect gyroid pyramids). But because we actually want to draw this promorph, we are forced to choose (because we cannot draw a general amphitect gyroid pyramid) one of its representatives, which most clearly displays the relevant features :  The 4-fold amphitect gyroid pyramid (expressing the Heterogyrostaura tetramera, i.e. Heterogyrostaura with four antimers). Something similar applies to displaying the promorph of the Crystal Class to be discussed next).

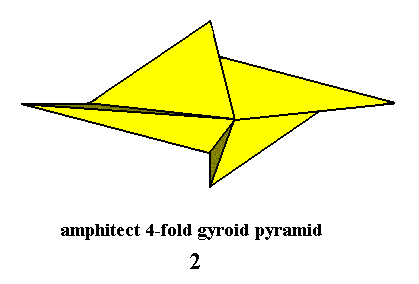
Figure 6.  Slightly oblique top view of an Amphitect Gyroid Pyramid, the Stereometric Basic Form of the crystals of the Sphenoidic Class of the Monoclinic Crystal System. The depicted pyramid allows for four antimers to be recognized.

In fact the Domatic Crystal Class  m  comprises all structures (with respect to crystals) that have a mirror plane as their only symmetry element (They correspond to the group  D₁ ,  which has two group elements, the identity and a reflection in a plane), and as such are compatible to (the promorphs of) the (homopleural) Allopola (Stauraxonia heteropola heterostaura), that comprise not only the Zygopleura eudipleura (i.e. bilateral forms in the strictest sense), but all (homopleural) Allopola (half amphitect pyramids), i.e. the other (homopleural) Zygopleura and all (homopleural) Amphipleura as well (For the difference between the Amphipleura and the Zygopleura, the reader should consult our Promorphological System).
To actually draw the promorph of the crystals of the Domatic Class, we have chosen  half a Rhombic Pyramid  and let it refer to the Zygopleura eudipleura, graphically representing all these possible promorphs.
And when we have a given crystal of the Domatic Class, we should, in order to assess the promorph, determine the number and arrangement of the antimers as we find them in the chemical motif of the (substance of the) crystal, as explained above (See for the classification of the Heterostaura allopola, as given below, HERE ).

Figure 7.  Slightly oblique top view of half a Rhombic Pyramid, the Stereometric Basic Form of the crystals of the Domatic Class of the Monoclinic Crystal System. The depicted pyramid has two antimers, indicated by coloration.

Figure 8. 
The basic form of the Heterostaura allopola, illustrated by half a Rhombic Pyramid (which itself is the basic form of the Allopola zygopleura eudipleura) .
Left image :   bisection face (originated by the bisection of the whole Rhombic Pyramid) emphasized (green).
Right image :   Base emphasized (green).
Main axis (vertical), lateral axis (horizontal) and dorso-ventral axis are indicated in red. The only symmetry element is the mirror plane, which contains the main axis and the dorsoventral axis. It separates the two antimers.

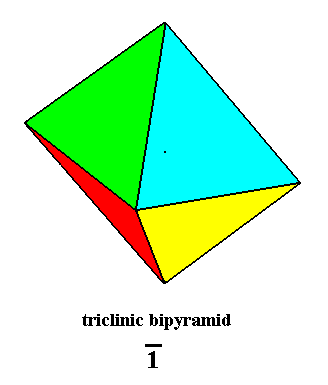
Figure 9.  Triclinic Bipyramid, Stereometric Basic Form of the Pinacoidal Class of the Triclinic Crystal System.
The angle between the equatorial plane and the main axis is different from 90⁰.

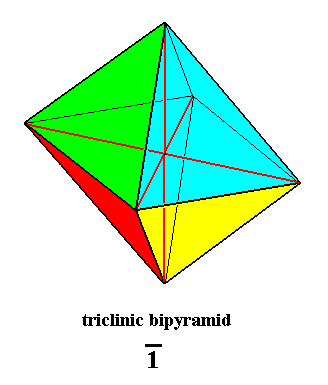
Figure 10.  Triclinic Bipyramid, Stereometric Basic Form of the Pinacoidal Class of the Triclinic Crystal System.
The angle between the equatorial plane and the main axis is different from 90⁰. Triclinic axial system inserted. The three axes do not involve angles of 90⁰.

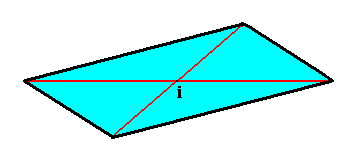
Figure 11.  Equatorial plane of a Triclinic Bipyramid, as seen from a direction perpendicular to that plane (and thus not seen along the direction of the bipyramid's main axis).
The angle between the equatorial plane and the main axis is different from 90⁰. Two triclinic axes inserted (red), they meet in the bipyramid's center of symmetry ( i ).

Organismic bodies, or their parts, generally do have macroscopic antimers (i.e. their structure is tectological, not periodic), and so their promorph is easily determined. Where no antimers are present the organismic body promorphologically belongs to the Anaxonia (bodies with no [promorphological] axes).
Let's summarize the above discussed promorphs.

Heterogyrostaura (and thus bodies with a promorph compatible with the symmetry group  C₂ ) may be found in some Diatomeans (unicellular algae with shells of silica).

Zygopleura eudipleura (and thus bodies with a promorph compatible with the symmetry group  D₁ ) are found in most animal bodies.

Anaxonia centrostigma (and thus bodies with a promorph compatible with the symmetry group  C_i ) could be expected among some virusses or some Radiolarians (marine unicellular organisms with complicated 'skeletons' often consisting of radially placed needles and concentric spherical shells).

•    Abstract group
•    Symmetry group
•    Promorph

To show that the promorph goes well beyond the corresponding symmetry group, it is perhaps instructive to enumerate all promorphs that can fall under the mentioned three symmetry groups,  C₂ ,  D₁  and  C_i ,  representing their possible promorphological differentiations (The three promorphs depicted above [Figures 6, 7 and 9] are highlighted) :

Heterogyrostaura (amphitect gyroid pyramids)
      Heterogyrostaura dimera
      Heterogyrostaura tetramera
      Heterogyrostaura hexamera
      etc.

Heterostaura allopola (bilateral forms in the broadest sense)
      Allopola amphipleura
           Triamphipleura
           Pentamphipleura
           Hexamphipleura
           Heptamphipleura
           etc.

      Allopola zygopleura
           Zygopleura eutetrapleura
                Eutetrapleura radialia
                Eutetrapleura interradialia
           Zygopleura eudipleura

Anaxonia centrostigma (bodies having no promorphological axes and no antimers, but which do have a body center)

Heterogyrostaura dimera
Heterogyrostaura tetramera
Heterogyrostaura hexamera
etc.

Triamphipleura
Pentamphipleura
Hexamphipleura
Heptamphipleura
etc.

Eutetrapleura radialia
Eutetrapleura interradialia
Zygopleura eudipleura

Anaxonia centrostigma

With respect to the above given three ontological layers, the abstract group does not presuppose any material entity, or, more generally, it does not presuppose any substrate that should receive it, or on which it should act, while the other two can do so. The symmetry group is still indifferent as to the dimensionality of the substrate, and also to the morphological, physiological, chemical or physical nature of the symmetries involved, indeed it could act on a totally abstract immaterial substrate, while the promorph, once it is given, relates to a determined dimensionality of the substrate, and involves a morphological interpretation of group elements.
For example, considering dimensionality, the symmetry group  D₆  could be that of a regular hexagon, but also that of a regular 6-fold pyramid. And they are different promorphs. In the same way the symmetry group  C₂  could be that of a two-fold plane figure (like, for instance, the letter  S ,  or an amphitect gyroid polygon), or expressing the symmetry of an amphitect gyroid pyramid, as depicted in Figure 6, and they too are different promorphs (The two-dimensional figures mentioned should belong to a 'promorphological system' of plane figures). Moreover, the amphitect gyroid pyramid can be further specified promorphologically as to its number of antimers (In this case, changing the (even) number of antimers into another (even) number does not change its symmetry, but it changes its morphology). So the (ultimate) promorph, once given, is more specific than the corresponding symmetry group.

The three levels -- abstract group, symmetry group, promorph -- will traditionally be seen as just abstractions from the structure of a given object (intrinsic thing), but in my opinion they together form one of the ontological causes of that given thing (The substrate is another such ontological cause). They are three metaphysical levels within that object. They are answers to certain what-is-it questions (questions relating to certain structural aspects of the given thing). They are not answers as to why and how they come to be associated with the given object. Such answers could be expected from considerations involving dynamical systems and initial conditions. Some investigators could maintain that the last mentioned considerations are at the same time providing the answer to the what-is-it question, but I do not agree with that position. Knowledge of the generation of certain structures and symmetries already presupposes the what-is-it of those structures and symmetries. And moreover, a same structure or symmetry could be generated in several ways. The answers to the why and how questions will ultimately relate to categories (expressed as basic predicates) in the sense of HARTMANN.

That entity, that consists of these three levels could be received in several different, but compatible, material substrates, and because of this it is still indifferent as to in what (compatible) substrate it is being received or acts on. So it is not yet a concrete entity, i.e. it is not yet a material entity having a specific trajectory in space-time. But once this is the case, we have the final ontological stage, an individual material (intrinsic) thing possessing that particular symmetry and promorph. Perhaps we could think of this ontological 'process' as some sort of emanation in the neoplatonic sense :  a descent from some highest metaphysical level via some intermediate levels all the way down to (prime) matter. But such an emanation should not be seen as an actual process that takes place somewhere, but expressing (aspects of) the metaphysical constitution of the given thing, which itself (i.e. the metaphysical constitution) expresses (aspects of) the what-is-it of that thing (I have written about emanation in the Third Part of this Website, which considers a holistic approach to the constitution of Reality).

Because the abstract group is wholly indifferent (with respect) to the material world, it surely must belong to a different domain of existence, which could perhaps be the Ideal Sphere of Being as proposed by Nicolai HARTMANN. We expect that all mathematical self-contained structures reside in this Ideal Sphere. This Sphere distinguishes itself from the Sphere of Real beings by the different way of being of its inhabitants. It is a way of being that does not involve time and matter and thus is devoid of genuine processes.
We could of course suppose that all mathematical structures, like abstract groups, turn out to exclusively belong to the real sphere of existence, and so could, although discovered by purely conceptual means, be abstracted from the things of the real world, while no ideal sphere of existence is present at all. This supposition can, however, be countered by the fact that there -- as far as I can see -- surely are some self-contained mathematical structures that contradict each other. This could be the case, for instance, with some disparate topological spaces. And such each-other-contradicting-structures could, because of their high degree of generality, not exist side by side in the Real Sphere of existence as abstractable structures. Hence there must be some different sphere of existence, which then would be Hartmann's Ideal Sphere.

The precise relationships, if any, obtaining between these Spheres of existence -- the Real Sphere and the Ideal Sphere -- are hard to assess. According to HARTMANN, 1940, Der Aufbau der realen Welt, pp. 41, it is not so that the entities (or some particular ones among them) of the Ideal Sphere represent (in the sense of are) the essence or principles (in the sense of his categories) of certain entities (residing) in the Real Sphere. As the things in the Real Sphere have their own principles within themselves, or at least within the Real Sphere itself, so also have the beings of the Ideal Sphere their principles within that Sphere itself. This could be so, but should not imply two completely separate worlds. And indeed, when doing Mathematics, we (as real beings) are, in one way or another, in contact with the Ideal Sphere. For the time being, I have characterized this contact such that it consists of a re-creation of some objects of the Ideal Sphere when doing Mathematics. But all this is not wholly satisfying. It's probably better to interpret the Ideal Sphere as a series or stack of metaphysical levels, the highest of which becomes, downwards along the stack, 'locally' further determined (specified) by the less abstract and thing- and process-oriented levels, which in turn can be received by a formless substrate and so constituting (not generating) material things. And this would imply that the Ideal Sphere is in some way enclosed within the Real Sphere, and so is not a disparate world after all. Within this all-encompassing world the constitution of things consists in the above mentioned emanation from the highest to the lowest metaphysical (ontological) levels. Indeed, in the next work to mention, HARTMANN (p. 281) insists upon the interpenetration of the Ideal and Real Spheres of Being, resulting in a partly overlap.

HARTMANN, 1935,  Zur Grundlegung der Ontologie, pp. 262, sees, as one of the reasons that prove the ontological self-containedness, in the sense of existential independence -- or, at least that prove their character to be that of beings --, of mathematical structures,  the possibility (as it turned out) of a mathematical treatment of, in principle, all natural (material) phenomena of the real world. So at least many concepts representing mathematical structures truly point to objectively existing entities, because if those structures were just the result of some sort of thinking-compulsion their ruling of the material world would be inexplicable. But, according to me, this argument has no bearing on the question at issue, because ANY relationship whatsoever between entities and processes in the real world could, in principle be treated mathematically :  In the old days one thought the planets to move in circles, and circles are mathematical objects. Later, however, they turned out to move in ellipses, but also these are mathematical objects accessible to mathematical analysis. And if those planets later turn out to move in egg-shaped orbits, or wobbling orbits, these too can be mathematically analysed, because they too are mathematical objects. And where, in Physics, some phenomena seem not to yield to mathematical analysis, one immediately sees this as due to the still insufficient state of contemporary mathematics, and one sets out to develop new mathematical theories that can deal with these phenomena, however weird they (and the corresponding mathematical theories) are. So the whole of mathematics (including future theories) has no special nature (and then "happens to be applicable" to the real world). HARTMANN seems to say :  Well, you have these mathematical structures, which are in many cases created in an a priori fashion by mathematicians (like the theory of matrices). But they must (at the same time) be different from pure fantasies, mind games or a priori constructions, because they turn out to rule certain phenomena in the real world (like the role matrices turn out to play in Quantum Theory (as matrix mechanics) which deals with the sub-microscopical domain of the real world). And, being thus not only a priori constructions of the mathematician's mind, means (HARTMANN) that they possess an objective existence (Ansichsein). But, as I've said, mathematical structures are not at all anything special, they could be any conceptual structure, provided they are each for themselves logically consistent. So, although it is true, it is meaningless to say that "Nature is mathematical".  It is equivalent to the saying that "Nature is natural"  (HARTMANN admits something like this on page 283 of the above mentioned work). And all this does not bring us any further than just our finding that in mathematics we've found a very efficient and exact language to argue about natural phenomena. But, in principle of course, we could have taken any appropriate language, also a verbal one, to argue about Nature. And whatever qualities, relations and laws turn out to be the ones of Nature, we describe it in that language. And this (including the use of mathematical language) implies concepts. These concepts are then supposed to stand for certain phenomena encountered in Nature, they are not those phenomena themselves, and thus do not enjoy an independent existence (Ansichsein), which automatically means that the relevant mathematical entities (which thus are equivalent to concepts and coherent sets of concepts) also do not enjoy an independent existence. So the argument that "Nature turns out to be mathematical" does not necessarily lead to the independent existence of mathematical structures, nor to their character of (being) beings, at all.

One could counter this by indicating that there nevertheless are structural features in the Real Sphere that are as they are by purely mathematical reasons, for example the fact that no real genuine single (i.e. non-twinned) crystal does contain 5-fold rotation axes in its repertoire of symmetry elements. Indeed one can mathematically prove that only 1-, 2-, 3-, 4- and 6-fold rotation axes can exist as symmetry elements of  p e r i o d i c  structures (where the internal structure of crystals is, by definition, periodic). So it seems, that here a certain mathematical feature determines corresponding real features. But a presence of 5-fold axes (in spite of the mathematics) in real crystals, only would mean a contradiction. In the present case the contradiction should read :

There is a real material structure that is periodic and at the same time not periodic.

So already for the Real Sphere a thing cannot be, say, A, and at the same time non-A. Consequently it is not a determination from and by the mathematical. In the mathematical, i.e. in the Ideal Sphere, we have just the same state of affairs with respect to any mathematical object. And in virtue of this we can derive the non-possibility of 5-fold rotation axes in periodic mathematical structures, i.e. we can derive a contradiction if we assume such an axis to be present. And we know that the material counterpart of contradiction cannot occur in the Real, that's why we then know that 5-fold rotation axes cannot occur in real material periodic structures.
One has nevertheless found real crystals that possess 5-fold rotation axes, but such crystals are not strictly periodic anymore with respect to their internal structure, so they are not crystals afterall, as long as we keep including  periodicity  of internal structure in the definition of a crystal.

• The a priori nature of mathematical structures.
• The relation between pure mathematics and applied mathematics.
• The indifference of mathematical structures with respect to the material world.

The fact that we have pure mathematics in addition to applied mathematics again emphasizes the independence of mathematics as a science, which points to an independence of existence of the entities it investigates, because there is no essential difference between the two. Any piece of pure mathematics can become applied mathematics. HARTMANN, 1935, p. 280, points out that "There is a thoroughgoing containment of ideal being within the real. The real world is formed-through [informed] and reigned-through [predominated] by ideal core relationships [...] One can also say :  Ideal Being functions in the Real Sphere as a sort of basic structure. And consequently the real world is intrinsically dependent upon it."  As has been argued above, this latter statement is not correct without proper qualification :  The real world turns out to be such and such (according to observation), and we then describe it with the appropriate mathematical structures, which evidently are not efficient causes. Their causal nature is ontological.
The independence of purely mathematical structures, like laws, is evident from the fact that we cannot obtain them from relevant real cases by exclusively empirical means (the latter only suggest one or several such structures). We can only obtain them by contemplating the simple basic relationships themselves, i.e. one can only get them in an exact way from (the sphere of) ideal being. That's what pure mathematics is doing. And when we want to apply them, these purely mathematical structures should then, after their elements have been physically interpreted, be tested by observation or experiment, and then, if necessary, be amended or replaced by other such mathematical structures.

Finally, the third argument of HARTMANN involves the indifference of mathematical structures with respect to their possible materializations in the Real Sphere of existence. He does, however, not distinguish between physically non-interpreted and physically interpreted mathematical structures. In what follows, I will so distinguish. With respect to this it should be emphasized that in the present document something being "interpreted" always is meant in an ontological sense, i.e. in the sense of something (finding itself as) being "connected to something else."
Purely, i.e. not physically or otherwise interpreted, mathematical structures, like the abstract group given in Figure 4, are indifferent as to their 'realization' in the material world. And there will be many mathematical structures that are not, were not, and will not, be realized in that world. A purely mathematical structure as such has nothing in it that links it up with the material world, it doesn't presuppose this world, it is totally indifferent with respect to it, not dependent on it. It exists on its own behalf.

HARTMANN tells us that this is not so the other way around :  The material world is fully dependent on certain mathematical structures. But we have seen that this is not so without qualification. The material world IS as it is, as we find out as a result of observations, and we then describe these results with the language of mathematics and generalize as far as seems possible. All this boils down to setting up mathematical models to describe and explain the relevant phenomena. So the purely mathematical structures, even when their corresponding models, which bear a physical interpretation of those mathematical structures, turn out to be wholly adequate, cannot be seen as (efficient) causes of the relevant phenomena of the natural (material) world, but as answers to what-is-it questions. They constitute the it-is-so, not the why-it-is-so. So an actual dependence of the phenomena of the material world upon purely mathematical structures is out of the question. The relevant mathematical structures are ontological causes, i.e. causes only in the sense of constituting (not generating) the what-is-it of those phenomena.
The efficient causes, i.e. the causes of generation, must be sought for in physical dynamical systems. And only as physically interpreted mathematical laws, the dynamical laws of such systems involve (true, i.e. efficient or active) causality. So when HARTMANN claims that the material world (which belongs to the Real Sphere of existence) is causally dependent on mathematical structures (or at least is determined by them as heteronymic entities (See below)), he should add that these structures must have the form of laws, and, moreover, should be in a physically interpreted state.
But the (physically interpreted) dynamical law of a dynamical system that generates a coherent physical structure, be it an organism, a crystal or some other object, is however also, and at the same time, an ontological cause, in the sense defined above, and as such is the Essence of such an object, residing in its "genotypic domain", while the products of the dynamical law (plus initial conditions) are (among many other features) the structure and symmetry of that one object, residing in its "phenotypic domain", i.e. at its ontological periphery (This is fully explained in the First Part of the Website). The fact of the necessary co-presence of initial conditions, and thus of the physical interpretation of the law, determines the physical nature of the dynamical system.
Such a (physically interpreted) dynamical law in its role of Essence, constitutes the what-is-it of the generated object (which here is a real individual independently existing object, like a crystal or an organism). As such it is comparable with, say, a symmetry group, which also constitutes a what-is-it. But there are two main differences between these two types of physically interpreted mathematical structures :
First, such a dynamical law also, and at the same time, physically generates that object (by organizing the elements of the corresponding dynamical system into one coherent whole, a 'totality'), while a symmetry group does not physically generate the symmetry of which it is the what-is-it.
Second, while the symmetry group is the what-is-it of a single pure feature (in the present case the symmetry of a given object), the dynamical law, as the Essence of the generated object, constitutes the what-is-it of the whole object at once, i.e. of all its features (and their mutual relationships) generated by that dynamical law. So this dynamical law is the what-is-it not only of the object's symmetry, but at the same time of all other aspects (as taken together) of the object's structure, composition and behavior. So this composed what-is-it of the object-as-a-whole, its Essence, is condensed into the one physically interpreted dynamical law. And this further means that this composed what-is-it is dynamic in character, while a symmetry group (constituting one pure feature only, and moreover, not generating it) is static.
The (mathematical) dynamical law all by itself, on the other hand, i.e. uninterpreted, is not of a physical nature. It does not generate, but only co-determines the what-is-it of the generated object-as-a-whole. And because purely mathematical structures are not physical structures, even in cases where they are moreover 'realized' somewhere in the material world, their way of being differs from that of physical entities (insofar as they are residing in the Ideal Sphere). They have -- what HARTMANN calls -- an ideal way of being, however not -- according to me -- residing in a separate world (which also HARTMANN denies) -- or in a (different) world that nevertheless partly overlaps with the Real World --, but present as metaphysical levels -- and so constituting the Ideal Sphere of existence -- within one and the same world. As physically interpreted, and thus as present in the Real Sphere, the way of being of mathematical structures is realiter.

HARTMANN says that the Real and the Ideal Spheres of existence both have their own categories, although many of them are common between them. A category is a determining principle, and as such it is an entity that is different from that what it determines, or, in other words :  a category is different from its concretum.
If we look to the Real Sphere we can say that the fundamental conservation laws are categories in this sense. They impose certain definite restrictions onto natural processes they so determine. But, of course, these laws, which are necessarily physically interpreted as to what physical quantities should be conserved, constitute a what-is-it. They do this, however, only partially, i.e. they form only a constituent of the what-is-it of the given process, a constituent that all relevant processes have in common. So a category in the Real Sphere is different from its concretum, but is nevertheless part of the what-is-it of the latter. It is a reality category in HARTMANN's sense.
In contrast to conservation laws, a physically interpreted dynamical law that thus relates consecutive states of a dynamical system, but implicitly contains the relevant conservation laws, constitutes the full what-is-it of the object (as-a-whole) that it generates, and so is identical to that what-is-it. But because the object is always also extrinsically determined, i.e. perturbed, by agents outside the generating system, there is no true identity between the what-is-it of the object and the object itself (and even already so when only the latter's qualitative content is concerned), because the what-is-it is meant to be the intrinsic (qualitative) content only.
In the same way we can say that the symmetry group IS (identical to) the symmetry of the given object. Also here we mean the object's intrinsic symmetry. Extrinsic agents (agents outside the generating system) perturb this symmetry, resulting in the fact that the what-is-it of the intrinsic symmetry of the object is not identical to the actual symmetry of that object  ( The latter symmetry can, of course, also be described by a symmetry group, which is, however, in most cases, the symmetry group  C₁ ,  which in fact means no symmetry at all ). It is precisely in virtue of these perturbations, as they constantly take place in the Real Sphere, that the concept of (intrinsic) what-is-it makes sense ( It is the very point of departure of the metaphysics of PLATO as well as that of ARISTOTLE ).

In all this, it is presupposed that there are objects that have something of  a  self, or identity, not in an anthropomorphic sense, but in the sense that they have some sort of identity core, so that we can, after some considerable effort it is true, distinguish between a qualitative "outer" and "inner" with respect to a thing or being, resulting first of all in the possibility to objectively distinguish between the constant intrinsic and repeatable features of it and the extrinsically variable features falling onto it, and secondly, to objectively distinguish between a genuine single unified thing or being and just an (extrinsic) aggregate (of such beings). This inner and outer is a central paradigm of the Substance-Accident Metaphysics of ARISTOTLE and St THOMAS AQUINAS. The First Part of my website is almost wholly devoted to verifying this supposition. It has its point of departure wholly from the individual material thing (whether it be a human person or a crystal individuum) insofar as it 'sees itself from within'. And this is a quite different approach from that of the ontology of Nicolai HARTMANN. The latter approach is, however, not because of that in error. It is complementary to my approach, and should be studied alongside the latter.

And it is in virtue of the absence of perturbations that in the Ideal Sphere the what-is-it of an ideal object is always totally identical with that object (implying, by the way, that in such an object the self is not conspicuously expressed). The actual symmetry of a hexagon as it (i.e. the hexagon) exists in the Ideal Sphere, is equal to the symmetry group  D₆ ,  i.e. this  D₆  symmetry group is not underlying the actual symmetry, but IS that very symmetry. Perturbations do not occur in the Ideal Sphere because they imply processes.
So to extract the what-is-it from an ideal entity is trivial, it is just that entity itself. What is not trivial is to analyse the what-is-it of an ideal object. We can then find ideal entities that, each for themselves, partially constitute that what-is-it. For example the Group Axioms (See below) partly constitute the what-is-it of the Abstract Two-element Group (Figure 4) (The other ideal entity making up and completing the what-is-it of that Group is its order of two (i.e. its two-elementness)). In such cases (i.e. concerning ideal objects) we'd better not speak in terms of analysing the what-is-it of an (ideal) object, but in terms of analysing the (ideal) object itself, resulting in its (explicit) what-is-it, which is wholly identical with that ideal object.
Entities within the Ideal Sphere, partially determining the what-is-it of other ideal entities, are ideality categories in HARTMANN's sense.

A Group is a set of elements, forming an algebraic structure in virtue of one operation (let us call it)  * ,  that satisfies the following conditions (which are the Group Axioms) :

• The operation  *  satisfies the associative property :
  If  a, b, c are any three elements of the group, then (ab)c = a(bc) holds.

• Every equation  x*a = b  and every equation  a*x = b  possesses one and not more than one solution.

1. Group Axioms  [The partial what-is-it of any Group, the general algebraic whatness].

2. Abstract Two-element Group  [Special algebraic what-is-it.  It contains the structure of 1 ,  but it is further determined as to the number of its elements. This number is  2 ,  which automatically implies that the non-identity element must be involute, i.e. its period must be  2 ].

3. Symmetry Groups  D₁ ,  C₂ ,  C_i   (and indeed also the corresponding antisymmetry groups  D₁ / C₁ ,   C₂ / C₁  and  C_i / C₁ ,  briefly discussed earlier ).  [ Elements interpreted. Presuppose object (abstract or concrete). The Symmetry Group is the what-is-it of the given symmetry. It contains the structure of 1 and (if it is one of the three mentioned groups) 2 .  The interpretation of the group elements can, to begin with, be purely geometrical, and if so, the group is still a purely mathematical structure (with its elements -- now being geometrical transformations -- related to each other algebraically). Such an interpretation can involve two-dimensional space (in which  C_i  and  C₂  coincide), or three-dimensional geometric space. The interpretation can, however, also be non-geometrical and involve symmetries of an abstract nature. In all these cases the symmetry group is still a purely mathematical structure.
   If, on the other hand, the interpretation of the group elements somehow involves physical three-dimensional space, then the interpretation is physical, and the corresponding symmetry group points to the real material world and is ontologically intermediate between purely mathematical structures and (the symmetry of) real material objects.].

4. Promorphs  Zygopleura eudipleura,  Heterogyrostaura,  Anaxonia centrostigma, and indeed all the promorphs mentioned earlier (Click HERE for overview).  [Geometrically morphological interpretation of group elements. Dimensionality implied. If a physical or chemical interpretation of the symmetry transformation can be reduced to a morphological state of affairs (microscopically or macroscopically), then the interpretation is (already) considered to be morphological. The Promorph is expressed as (the simplest possible) geometric solid. It is the geometric what-is-it of morphological symmetry. It implicitly contains the algebraic structure of 1, and in the present cases, that of 2 and 3 .  It moreover shows the number and nature of the antimers, even where this number does not co-determine the given symmetry (as we could specify the Heterogyrostaura as : Heterogyrostaura tetramera or as Heterogyrostaura dimera, both having  C₂  symmetry (See below)).
   The group elements, so interpreted (resulting in the corresponding promorph), yield a mathematical structure of which the interpretation is such that it also directly points to certain beings in the real material world, and as such also is ontologically intermediate between purely mathematical structures and (the symmetry and some other aspects of the structure of) real material objects. ].

Antimers or counterparts are identical or (more or less) similar parts of a natural body, say an organism or a molecular chemical complex, that are (more or less) regularly arranged around that body's main axis, for example, the two body halves of a human body, the five arms of a common starfish, the five rays (radii) of a regular or irregular sea urchin, etc.  As such these antimers are geometrically indicated in the geometric solid expressing the corresponding promorph of that given natural body.

First, these promorphs (of the just mentioned list) are special interpretations of those symmetry groups :  They are specified as to be three-dimensional geometric closed figures pointing to material objects. In this way we get -- within the overall layer of the relevant promorphs themselves -- a  first geometric what-is-it layer,  namely the three general promorphs, respectively associated with our three symmetry groups :

• Heterostaura allopola (bilateral forms in the broadest sense,  half amphitect pyramids)  ( D₁ ).
  
• Heterogyrostaura (amphitect gyroid pyramids)  ( C₂ ).
  
• Anaxonia centrostigma (triclinic bipyramids)  ( C_i ).

With respect to the symmetry group  D₁ ,  the Heterostaura allopola can be further determined (specified) to

• Allopola amphipleura (half amphitect pyramids with  4+2n  sides ( n = 1, 3, 4, 5, .  .  . ), and
  
• Allopola zygopleura (half a rhombic pyramid, or, equivalently, an isosceles pyramid).

The Allopola amphipleura can be further, and finally, determined to

• Triamphipleura (half six-fold amphitect pyramids),
  
• Pentamphipleura (half ten-fold amphitect pyramids),
  
• Hexamphipleura (half 12-fold amphitect pyramids),
  etc.

The Allopola zygopleura can be further determined to

• Zygopleura eutetrapleura (half a rhombic pyramid [isosceles pyramid] with four antimers), (or, as second possibility, a trapezoid pyramid), and, as final determination, to
  
• Zygopleura eudipleura (half a rhombic pyramid with two antimers).

The Zygopleura eutetrapleura can be further, and finally, determined to the

• Eutetrapleura radialia (bi-isosceles pyramid with two symmetrically equal lateral halves), and
  
• Eutetrapleura interradialia (trapezoid pyramid with two symmetrically equal lateral halves).

The Zygopleura eudipleura cannot be further determined (specified).

• Heterogyrostaura dimera (amphitect gyroid pyramid with two antimers),
  
• Heterogyrostaura tetramera (amphitect gyroid pyramid with four antimers),
  
• Heterogyrostaura hexamera (amphitect gyroid pyramid with six antimers).

It is perhaps instructive to elaborate a little more on   p r o m o r p h s ,  because they probably are not familiar to any reader [except when he or she has read our exposition of the system of promorphs (Promorphological System of Basic Forms) on this website], and also because of their importance for a general theory of structure of material things.

The symmetry according to the symmetry group  C₂  can promorphologically be expressed as an amphitect gyroid pyramid. The only symmetry element that such a pyramid possesses is a 2-fold rotation axis (Recall that in cases of geometric symmetry a symmetry element is a point, line or plane, with respect to which a symmetry transformation is performed). But while this symmetry (C₂) staying the same, the number of antimers can nevertheless vary among the even numbers. And this number of antimers (corresponding to certain definite body parts (in organisms) or chemical units (in crystals)) is expressed by the Promorph (by its name as well as by the geometric solid representing it). In the next Figures we discuss two possible numbers of antimers in the Heterogyrostaura, represented by amphitect gyroid pyramids.

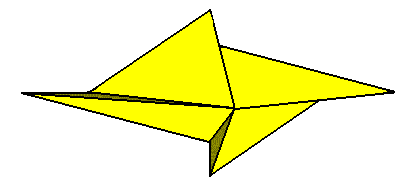
Figure 12.  Slightly oblique top view of a four-fold amphitect gyroid pyramid representing the Heterogyrostaura tetramera. This promorph represents natural gyroid bodies, compressed perpendicular to their main axis, and having four antimers. The symmetry is that of the symmetry group  C₂ .

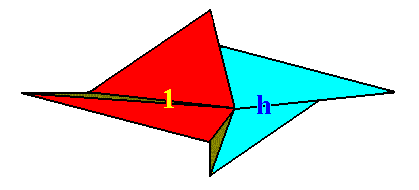
Figure 13.  Four-fold amphitect gyroid pyramid representing the Heterogyrostaura tetramera. This promorph represents natural gyroid bodies, compressed perpendicular to their main axis, and having four antimers. The symmetry is that of the symmetry group  C₂ . The body parts of the pyramid representing the two group elements  1  and  h  are indicated (red, blue), where  1  stands for the identity element, while  h  stands for a half-turn (rotation by 180⁰ about the pyramid's main axis).

The next Figure shows the four antimers of the amphitect gyroid pyramid of Figure 12.

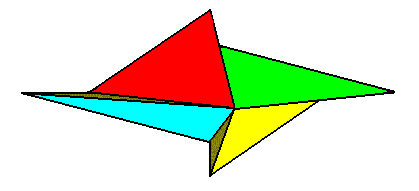
Figure 14.  Four-fold amphitect gyroid pyramid representing the Heterogyrostaura tetramera. This promorph represents natural gyroid bodies, compressed perpendicular to their main axis, and having four antimers. The symmetry is that of the symmetry group  C₂ . The body parts of the pyramid representing the four antimers are indicated (red, green, yellow, blue).

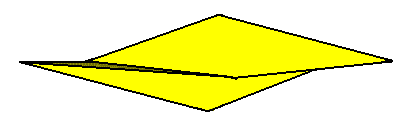
Figure 15.  (As in the previous Figures) slightly oblique top view of a two-fold amphitect gyroid pyramid representing the Heterogyrostaura dimera. This promorph represents natural gyroid bodies, compressed perpendicular to their main axis, and having two antimers. The symmetry is, as it was (also) in the Heterogyrostaura tetramera (previous Figures), that of the symmetry group  C₂ .

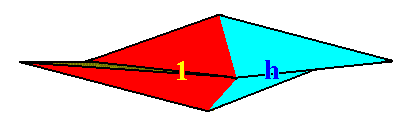
Figure 16.  The body parts of the 2-fold amphitect gyroid pyramid (which is the promorph of the Heterogyrostaura dimera), that can represent the two group elements  1  (identity element) and  h  (half-turn), are indicated (red, blue).

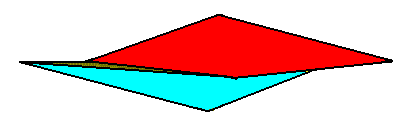
Figure 17.  The body parts of the 2-fold amphitect gyroid pyramid (which is the promorph of the Heterogyrostaura dimera), that can represent the two antimers, are indicated (red, blue). But, of course, we could, in the present case, let the antimers coincide with the body parts representing group elements.

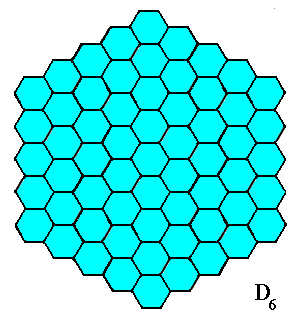
Figure 18.  A two-dimensional hexagonal object. Its symmetry (point symmetry) is that of  D₆ .  It has, however, no genuine antimers.

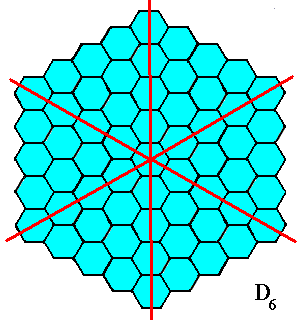
Figure 19.  The mirror lines (red) of the object of the previous Figure suggest the presence of six antimers, but the next Figure shows that the structure of their boundaries is not unique.

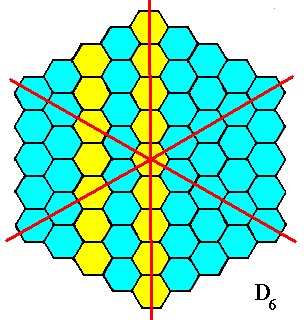
Figure 20.  The mirror lines of the object of Figure 18, as indicated in this and the previous Figure, cannot represent boundaries of antimers, because the morphology of these alleged boundaries is not unique, and thus they do not morphologically distinguish antimers.

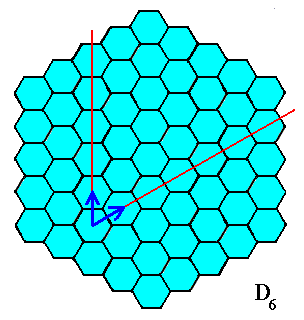
Figure 21.  Translation vectors of the lattice that underlies the pattern of Figure 18.  (The pattern must be imagined to extend indefinitely in 2-D space). If we eliminate all translations, we are left with one smaller homogeneous hexagon, which also does not have genuine antimers.

Figure 22.  Translation-free residue of the pattern of Figure 18  ( The latter imagined as being extended indefinitely in 2-D space). It has still  D₆  symmetry and possesses no antimers.

Figure 23.  Test of a recent sea-urchin (sanddollar), with (natural) indications of the five antimers (extending also internally) which together build up the whole animal. Although almost regularly 5-fold, the animal is only bilaterally symmetric and possesses a mirror plane as its only symmetry element. Its symmetry therefore is that of  D₁ .  This group has two group elements, namely the identity element and the reflection in the median plane. The general  promorph  of the animal, is half a rhombic pyramid (as in Figure 7), or, still more generally, half an amphitect pyramid, and so belongs to the (general) (Heterostaura) Allopola. It has, however, five (similar) antimers, and so does not belong to the Allopola zygopleura. The true promorph of the body of this animal is half a 10-fold amphitect pyramid, expressing in this way the possession of five antimers and implying the promorph to belong to the  Pentamphipleura  (itself being a species of the Allopola amphipleura).   See next Figure.

The next Figure shows the promorph of the test (and with it of the whole animal) of the sea urchin as dipicted above. It is half a 10-fold amphitect pyramid. The five antimers are indicated by colors. They form the five 'rays' of the animal.

Figure 24.  Oblique top view of the promorph of the bodies of irregular sea urchins. It is half a 10-fold amphitect pyramid with the five antimers (corresponding to five body parts in the animal) indicated by colors. It therefore belongs to the  Pentamphipleura  (Allopola amphipleura). The brown plane facing the beholder is the bisection face associated with the bisection of the 10-fold amphitect pyramid.

Having expounded the meaning and significance of the Promorph, we can now return to our (special) scheme of whatnesses  :  Group Axioms, Abstract group, Symmetry group and Promorph, in order to assess their ontological status more precisely. Before we do so, we first state some generalities about the Ideal and Real Spheres of existence, and about the manner of geometrically representing a promorph.

Generally we can say that the mode of determination in the Ideal Sphere is Logical, while the mode of determination in the Real Sphere is Causal.

That the only mode of determination in the Real Sphere is causal, will not be accepted by every thinker. First of all we have the submicroscopic domain (quantum domain) of the Real, where strict causality seems to be absent. I suspect, however, that future research in the subquantum domain will reveal the hidden causes, responsible for the statistical 'determination' of quantum systems.
But also in the so-called higher domains of the Real -- namely the domain of human behavior and psychology --, causality is denied by many philosophers (mainly on the basis of an assumed free will [ See for a discussion of free will, First Part of Website Organisms IV ] ). Me thinks this position originates from illegally ontologically hypostatizing certain aspects of human experience and behavior (For example saying that a human being has a soul, where the latter is supposed to be some more or less independent entity). See below, where this is discussed further.

In the Ideal Sphere the assessment (and concept) of the what-is-it of an ideal entity is trivial, because it is that entity itself. This what-is-it can however be analysed as to its constituents. Or one can depart from such a constituent and determine what it presupposes. All this belongs to what pure mathematics is doing.
If, within the Ideal Sphere, some ideal entity A is part of the what-is-it of some other ideal entity B, then we can say that A (partially) determines B.

In the Real Sphere the what-is-it of a real object is its intrinsic qualitative content. In the Real Sphere there is consequently room for extrinsic qualitative content as well.

When some entity is a category (in HARTMANN's sense), it is different from that what it determines (its concretum), and so cannot be indicated by the same  n a m e  as that of its concretum :  It is a heteronymic entity.
If some entity constitutes the whole what-is-it of some object, it can be indicated by the same name as that of the object (which is -- or should be -- named after its intrinsic content, which is its what-is-it) :  it is a homonymic entity.

The promorph is, in all cases, represented by a purely geometric solid, like a pyramid, an endospheric polyhedron, a cone, etc. This solid is, to begin with, the simplest geometric solid expressing the symmetry of a given material body (say a crystal or an organism) of which it is the promorph. But the promorph goes beyond expressing the symmetry of such a body. It expresses the number and arrangement of the body's antimers (and so spills over into other aspects of structure than symmetry alone).
In many cases this number (which is called the body's homotypic number) is wholly linked up with the symmetry of the given body :  The common starfish, for example, has five congruent antimers (five congruent body parts regularly arranged around the body's main axis), and its promorph can be expressed by a regular 5-fold pyramid. And although the unique morphology of the boundaries (or of the mid-lines for that matter) of the animal's antimers cannot be fully expressed geometrically (as long as we insist upon simple solids), it can, in the present case, be indicated (but not more than that) by the five upright edges of the pyramid, coming together at the pyramid's apex. See next Figure.

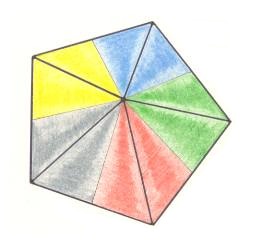
Figure 25.  Slightly oblique top view of a five-fold regular pyramid as the basic form of the Pentactinota (Stauraxonia heteropola homostaura), expressing the promorph of the body of a common starfish. The spatial extension of the five antimers is indicated by colors.

Figure 26.  Oblique top view of the promorph of the body of a common starfish.
Left image  :  Even if there are in the animal some morphologically unique boundaries as indicated in the image by the red-blue transitions, the boundaries of the antimers (indicated by dark blue lines extending beyond the image proper) are still the same as they were in the previous Figure.
Right image  :  If we want to express the global and relevant antimer boundary morphology geometrically, i.e. if we want to express, in a purely geometric way, the uniqueness of the vicinity or neighborhood of the boundary lines (blue extending lines) between the antimers, then we obtain a  complicated  (instead of a simplest possible) geometric solid, as indicated in this image.

Anyhow, the five antimers of the starfish are directly responsible for the five-fold symmetry of the geometric solid representing its symmetry. And the symmetry of the starfish all by itself already indicates its five antimers.
In other cases, however, the number of antimers (homotypic number) is not implied or indicated by the symmetry of the given material body, like we saw in the case of, what one calls, irregular sea urchins. There, the simplest geometric body expressing their symmetry -- which is that of the symmetry group  D₁ -- is just half a rhombic pyramid (See Figure 7). This pyramid does not, however, indicate at all, the  five antimers of the animal, but suggests two (by its right and left halves). So in order to (at least) indicate these  five antimers, the promorph must be represented by half a 10-fold amphitect pyramid, as in Figure 24, i.e. by a slightly more complex geometric solid than half a rhombic pyramid is. In this pyramid the five edges (i.e. five of the ten edges that were originally the upright edges of the 10-fold amphitect pyramid converging in the pyramid's apex) do indicate (but, as always, not more than that) the presence of the five antimers of the sea urchin. So, not half a rhombic pyramid, but half a ten-fold amphitect pyramid turns out to be the simplest geometric solid, representing the symmetry of the mentioned sea urchin and at the same time indicating its five antimers. In the mentioned Figure the antimers are, as to their extension, indicated by colors.

The upshot of the foregoing is that a geometric solid, insofar as it is the simplest geometric solid expressing the relevant symmetry and the rest of the promorph, cannot fully express the antimers present in some given body. It can only indicate (the presence of) the antimers. And as such, i.e. in so indicating, it IS not, but only refers to, a genuine morphology that is actually present in some given material body, i.e. it refers to physical antimers. So a promorph, although it is still general, presupposes the Real Sphere of existence.

• The Set of Group Axioms as such is an ideality category :  It resides in the Ideal Sphere and constitutes a part of the what-is-it of every abstract group (and also of every interpreted group for that matter), its concretum, also -- as abstract group -- residing in the Ideal Sphere. As such the Set of Group Axioms is a heteronymic entity.

• The Abstract Group in turn is also an ideality category, namely in the case where it constitutes a part of the what-is-it of a purely mathematically interpreted symmetry group. As such it is a heteronymic entity. Like the Set of Group Axioms it can never be a reality category, because they are both totally abstract, and thus cannot actively determine.

• The Symmetry Group is an interpreted group, and it belongs wholly to the Ideal Sphere, provided its group elements are purely mathematically interpreted. When its group elements are geometrically interpreted, even when involving 3-dimensional geometrical space, it still belongs to the Ideal Sphere, but, when from there it is further interpreted, involving antimers, which are necessarily physical, it becomes a promorph, which is ontologically intermediate between the Ideal and Real.
  If the group elements of a symmetry group are physically interpreted, i.e. if the group finds itself in a physically determined state, which means that each group element is represented by some physical asymmetric, but not yet further specified, structure or unit (See Figure 27), the group's ontological status is then intermediate between the Ideal and Real, because it is still general. It could, for example, be one or another physical body having the shape of half a rhombic pyramid. The two composing asymmetric quarter pyramids (separated by the median plane of that half-a-rhombic-pyramid) then represent the two group elements :  the identity transformation and a reflection in the median plane.
  If the symmetry group is the what-is-it of the symmetry of some given individual material object (i.e. if it is its intrinsic symmetry, which is not necessarily the same as its actual symmetry), the group so conceived, exists realiter (not as a thing, but as an ontological constituent). With respect to this symmetry the symmetry group is thus a homonymic entity, and so not a category.
  Considering things in the Real Sphere, we cannot say that the physically interpreted symmetry group (actively) determines part of the (whole) what-is-it of the given object (possessing the relevant intrinsic symmetry), because no causality is involved here (which is the only mode of (active) determination in the Real Sphere). It does not determine, but IS part of the (whole) what-is-it of that given material object.

• The ontological status of the Promorph is intermediate between the Ideal and the Real Spheres, because, a promorph is not purely geometrical, it refers to the material world. This is because the group elements of the corresponding symmetry group are interpreted as (sets of) (physical) antimers (See next Figure). Insofar as a promorph is materialized in an individual physical body (a crystal, or organism), it exists realiter (not as a thing, but as an ontological constituent).
  The promorph does not causally determine the symmetry or structure of a material object, and so it is not a category. It IS the intrinsic symmetry of that object (because it presupposes the corresponding symmetry group), and is at the same time a certain aspect of the structure of the given object, not necessarily tied up with its symmetry, namely the number and arrangement of the object's antimers. And as we saw earlier, the promorphological layer itself often consists of several layers, which in the Real Sphere eidetically determine from higher to lower (i.e. the higher promorphological layers are parts of the what-is-it expressed by lower-layer promorphs), while as residing in the ontologically intermediate domain, the higher-level promorphs relate logically (as the mode of determination in that domain -- and in all non-real domains for that matter) to the lower levels.

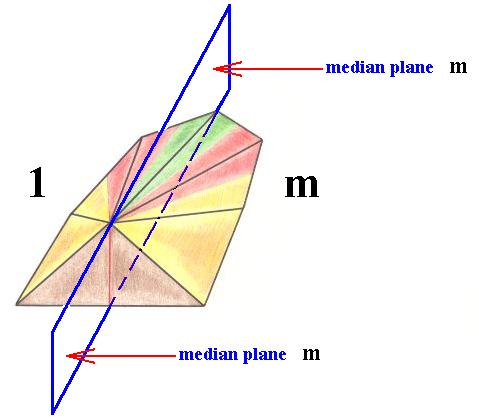
Figure 27.  Half a 10-fold amphitect pyramid representing the promorph of an irregular sea urchin (Figure 23). The latter's five antimers are indicated by colors. The median plane is a mirror plane and as such the only symmetry element of the sea urchin's symmetry. The symmetry group therefore is  D₁ .  This group has two group elements, namely the identity element  1  and the reflection in the median plane  m .  In the promorph they are represented by its two halves separated by the median plane. These halves are asymmetric units. But, as can be seen, each such a half -- representing a group element -- consists of two-and-a-half antimers, so each group element is -- in the present case -- interpreted as a certain set of antimers (more precisely, as a set of five half-antimers, or, equivalently, by two and a half antimer).

The physically interpreted dynamical law of a given totality-generating dynamical system is immanent in the elements of that system, and so its way of being is real. As such it is a here-and-now case of a special reality category, residing in the dynamical system (which is its concretum), and determining causally. It will however, at the same time become the essence of the generated individual totality, and as such determining eidetically, i.e. constituting its intrinsic content or what-is-it.

The non-interpreted dynamical law is just a Form. It is not a reality category anymore. It is part of the whatness of the interpreted dynamical law and thus also part of the whatness of the totality generated by the latter. As such it is only eidetically determining, i.e. it just constitutes (part of) a what-is-it.
Because the non-interpreted dynamical law does not as such (i.e. by definition) inhere in a real dynamical system -- it is just a mathematical structure -- its way of being is ideal. It is only real when the law is physically interpreted. If the (physical) interpretation is such that the law is still general, its ontological status is intermediate between the Ideal and the Real Spheres of existence.
Within the Ideal Sphere this non-interpreted dynamical law is a 'concretum' based on, and dependent on, certain ideality categories.

We now try to assess these Spheres of existence more closely, on the basis of the above obtained results.
HARTMANN, 1935, p. 281, says that (some of) the General -- and thus (some of) the Ideal -- is present in the Real (Sphere) (and, of course, also the individuality aspect is present in the Real). Thus the two Spheres interpenetrate (but not totally overlap) each other.
It is reasonable, however, to say that the 'General' (residing) in the Real necessarily becomes individual. And thus the 'Ideal' as it is in the Real, i.e. in cases where it happened (also) to reside in the Real, exists there realiter.
The Ideal is only truly Ideal, as existing beyond the Real in another Sphere, namely the Ideal.
Indeed, in cases where some mathematical structure is in the Real, it finds itself as necessarily and automatically physically interpreted (i.e. as such it is in a physically specified condition). And -- in cases where that mathematical structure is a law -- the Real is determined by something real.
So as soon as a purely mathematical structure -- be it a (mathematical, i.e. pre-physical) law or a basic aspect of a what-is-it -- which in itself is general (as to its possible interpretations, mathematical or otherwise), somehow ends up in the Real, it is physically interpreted and becomes real and individual. Its 'generality' in the Real is not genuine generality anymore. It is from case to case individual, and thus real (not ideal), i.e. it is realiter.
Only non-physically interpreted mathematical structures are genuinely (i.e. ontologically) general and thus ideal. And mathematical structures, physically interpreted, but abstracted from all individuation conditions, are to be considered as belonging to an intermediate ontological layer.
HARTMANN clearly misses to consider the distinction between physically interpreted and non-interpreted purely mathematical structures. The fact that not-in-any-way-physically-interpreted mathematical structures can be known-and-studied a priori, i.e. in the complete absence of physical realizations, and also the fact of the possibility of making errors which eventually can be discovered and amended, proves their objective and independent existence, i.e. independent of the Real, meaning that their way of being is ideal (See HARTMANN, 1935, p. 279/280, and also p. 297). Physically interpreted mathematical structures cannot be known a priori.
With respect to the gnoseological (i.e. in the process of acquiring knowledge) assessment of the what-is-it of a given property of a certain material object, one first eliminates all individuation conditions of that object, i.e. one carries out an abstraction. Here this means eliminating all here-and-now conditions, resulting in a (qualitative) content only. What one so obtains is something general, in the present case concentrating thereby on that given property. Then one ponders about the essentials of that so-obtained-property-in-its-generality, ultimately ending up with its pure what-is-it.
In the case of the symmetry of a given material object one so obtains first the appropriate promorph (i.e. one mentally depicts a graphical image representing that underlying essential symmetry, i.e. the symmetry lying beneath the observed symmetry -- the latter is often an asymmetry). This surfaced symmetry is then further analysed as to its general underlying algebraic structure, yielding first the relevant symmetry group and then the corresponding abstract group. The total result is then the fully explicit what-is-it of the intrinsic symmetry lying beneath the observed symmetry of that given object.
With respect to the way of being we can say that as soon as we have accomplished the above mentioned abstraction, we see (in the sense of : we then encounter) that same given property as it exists in the Ideal Sphere of being, because it is now general. In its form as promorph or symmetry group it, when abstracted from a real (material) object, however, still points to the Real Sphere of being, i.e. presupposes that Sphere, and thus constitutes an intermediate metaphysical layer, a layer between the fully abstract (and thus non-interpreted) group and the empirically given symmetry and some other aspects of structure, of the given material object.
Only as not physically interpreted, the mathematical structure is indifferent to the Real, and as such it is then purely ideal. When it is just purely geometrically interpreted (and thus not actually abstracted from a real (material) object), it belongs wholly to the Ideal Sphere.

Are the Real and Ideal Spheres the only Spheres of objective existence, or are there still other such Spheres in addition to them? Let's try to answer this question.
A given qualitative or structural content, taken all by itself, i.e. a given being-thus (Sosein), can only legitimately be called a genuine content if it has at the same time existence, i.e. being-there (Dasein).
Existence, in this condition of existence, is, however, not restricted to the Real Sphere only. It may be existence in the Ideal Sphere. These Spheres differ in the way of being-there of their inhabitants. And with respect to the Real Sphere, existence is not restricted to the present. It may be existence in the past or in the future as well. Where, in time, something exists in the Real, depends on the prevailing total collocational dependency network in the Real.
This implies that so-called contents which 'are' only in the mind without any existence also in the Ideal or in the Real, are not contents at all, like for instance a phoenix (which is supposed to be a bird that can arise again from its ashes). One could counter that a phoenix is as such definable, but it is not (It is only so in a formal context, not in an ontological context). Otherwise 'everything' would be definable, resulting in effect that nothing would be definable. And even apart from this, i.e. even when something that does exist objectively, is, as a concept, in the mind, it is not as such, i.e. as (the content of) that thing, in the mind, but only as a (natural) sign which points to that particular object (in the sense of thing) or property, whether existing in the Real or in the Ideal.
So objects (things), or contents, do not exist in the mind at all. The so-called being-present-in-the-mind has no ontological significance, because the relevant structures in the mind only represent such objects or contents, by means of (natural) signs.
So the only spheres of existence are the Real and the Ideal.
A phoenix not only does not exist in the Real, it also does not, and cannot, exist in the Ideal either, because it does not correspond to (in the sense that it is not) some coherent ideal structure or pattern. It presupposes the Real by its allegedly being able to reappear from its ashes, which is supposed to be an essential quality of it. This quality cannot exist in the Ideal because it is definitely supposed to be a quality which is inextricably bound up with the Real, and only the Real, because a process is supposed to be involved. So the concept of a phoenix cannot represent some coherent structure in the Ideal.
Whereas a concept, pointing to an existing entity (existing in the Real or Ideal) is a neurophysiological event that we can legitimately call a sign, the 'concept' of a phoenix is only a neurophysiological event and nothing more (in the context of this discussion), i.e. it is not a content (other than that of the neurophysiological event itself), nor pointing to a content.
So, again, every genuine content has existence (realiter or idealiter), and (we can add) every existing entity has a content.
Earlier, we have postulated an intermediate ontological level, i.e. a level between the Real and Ideal. So in a sense we here have a third ontological domain in addition to that of the Real and that of the Ideal. This is necessary, because we are supposed to live in ONE world :  The Ideal and Real must somehow be connected with each other.

The upshot of the above discussion concerning existence in the mind, is that all kinds of so-called 'higher' entities, properties or behavior, which we could collectively call the (products of the) human spirit, do not have any ontological significance. They are at most more or less analogous to genuine beings or properties, real or ideal. Their significance lies in our daily life and in our participating with, or co-creating, a culture, in which philosophy, science, religion, rules of conduct, history, etc. play a role. This means that the 'being' of the Spiritual only appears within the narrow confines of a very specific and derived context bound up with the human condition and possessing meaning only within this narrow context (like for instance ethical values). In a more general and broader context the Spiritual is meaningless and nothing more than some neurophysiological activity.
I realize (and have actually experienced) that such a position touches on a sore spot of many (if not most) philosophers. The mentioned position is, however, not meant to be a once and for all established absolute truth. It is meant to trigger further dialogue. Indeed, on this very website I have presented an alternative view, based on the Theory of the Implicate Order of David Bohm (You can find it in the Third Part of Website :  a  HOLISTIC Philosophy as an alternative world view ).
The more or less reductionistic position outlined in the present document also makes clear why I cannot accept HARTMANN's division of the Real into several ontological layers ( HARTMANN, 1940, Der Aufbau der realen Welt ), of which the lowest represents the Physical, and the higher the Organic and finally the (objectively) Spiritual, i.e. the (mentioned products of the) Human Spirit. And in line with this, some typical physical categories (ontological principles determining the Physical) prevailing in the lower layers, are supposed to break down in the higher, implying that the differences of the layers are ontological. In my opinion they are not. Their difference boils down to different degrees of material complexity of the corresponding beings (say, atoms in the lowest layer, and cats in some higher layer, and human cultural institutions in the highest layer). So the ontological status of a salt crystal and of the queen of England is exactly the same. Both are just beings within the Real Sphere of existence. But the complexity of human beings is so immense that it can create pseudo-entities that strongly suggest some sort of ontological sublimity of the Human Spirit which is then supposed to be inaccessible to mathematical or physical analysis, even in principle, because the categorical make-up of this Human Sphere is (supposed to be) fundamentally different from the Physical. But of course, nobody can deny beforehand the capacity and appropriateness of future mathematics and physics in explaining the Human Spirit, because that would be tantamount to be able to predict the future development of mathematics and physics, which of course, nobody can.
I think the strongest and most compelling indication of the equal ontological status of all real beings (i.e. all beings of the Real Sphere of existence) is their cosmic and biological evolution from simple precursors, in which functional complexity and variety ultimately increases all the way up to staggering degrees, perplexing the self-contemplating featherless biped, and tempting him into hypostatizing his own mental creations and institutions that flow (without him knowing this) from his complexity. But eventually he will realize that these emergent events, i.e. his spiritual experiences, events and entities, are just consequences of his delicate structural complexity, and when the latter disintegrates so do its treasured epiphenomena. The latter are utterly dependent upon his subtle physiological make-up. Only by way of prolonged evolution will they persist for some short cosmic while.
So it is the power of physical and physiological dynamical systems that generates the (complexity of the) domain of the Human Spirit which is therefore inextricably bound up with the body, and thus with physical matter, and ontologically on an equal footing with the latter.
Of course, there could be absolute limits as to our understanding the Human Spirit (as there are already such limits within mathematics), but these limits are gnoseological in character, not ontological.
All this implies that the Real Sphere of existence is ontologically homogeneous, and that the layers in it are just different levels of material complexity, showing more or less abrupt leaps here and there when we ascend in contemplation from atom and crystal to organmism and human being. However, it may be possible to mitigate this position, and then nevertheless establish several layers within the Real, along the lines proposed by HARTMANN, but with definite amendments. I have attempted this in Part I of  Fourth Part of Website .

HARTMANN, 1935, pp. 298, rightly emphasises the fact that Logic is not a system of thinking laws. The latter are psychological (and are ultimately effects of the relevant dynamical system), not logical. We apply logical laws to our thinking about independent entities -- be they mathematical or real entities -- because they turn out to work properly, and give us a feeling of truth. The logical element in this thinking has -- according to me -- appeared a posteriorily in our thinking behavior during our organic evolution. This is also implied by what HARTMANN says on p. 305 (end of 48th Chapter).
That logical structures seem to rule all real events is, however, not a valid argument in favor of some independent existence of logical structures, in virtue of precisely the same reasons as I have put forward earlier with respect to the mathematical. If some domains of the Real turn out to behave differently, i.e. different from our usual Logic, then we adapt the latter (while retaining consistency) to accomodate observed fact. This could result in several different logical systems coresponding to different and more or less self-contained domains of the Real.
Only the fact that (1) logical systems can be investigated a priori, i.e. in the complete absence of cases of the Real, and the possibility of making, discovering and subsequent correction of, errors, and (2) the fact that we, by reasons of internal consistency, cannot erect just any logical system we wish to (in the same way that we cannot erect complex numbers each consisting of three elements, in the case of mathematics), the independent existence of logical entities or structures is sufficiently demonstrated.
Logic (or systems of Logic) is a general and precise language by which we can describe the fundamental relations as they turn out to be within the Ideal Sphere of existence. It expresses the coherence and connection between mathematical entities.

In all the foregoing we have spoken about several "Spheres of existence", differing in the way-of-being-there of their inhabitants, namely the Ideal and Real Spheres in the sense of Nicolai HARTMANN. We found out that mathematical and logical structures have an independent existence in the Ideal Sphere of Being, and that they are indifferent as to their possible 'realization' within the Real Sphere. Only when those structures are each for themselves coherent and consistent can they be genuine beings in the Ideal Sphere.
With respect to the Real Sphere, we found out that it is ontologically homogeneous, in the sense that its different inhabitants do not effect or represent different ontological layers within that Sphere. There can, however, be some sort of ontological layering, but only in such a way that the same whole system of layering cuts across every being of that Sphere (so that every being remains ontologically equivalent to any other being in that Sphere). This layering could consist of metaphysical levels or layers, going from the fully abstract (i.e. no qualitative content, or, perhaps equivalently, bare relations without (specified) relata), via intermediate levels, down to the fully determined concrete individual real being. And this stratigraphy is the same for every such being. In this way we go from the Ideal Sphere, via intermediate levels, down to the Real Sphere.
The system of layering just mentioned, is metaphysical (ontological) in character. Let's explain.
It consists of an ordered set or stack of general conditions that are absolutely necessary for something to be a real being at all (implying that these conditions are not beings themselves). This set of conditions is the same for every real being, and the conditions themselves are not specific with respect to one or another qualitative content.
For something whatsoever to be  a  genuine being  in the first place (real or ideal), it must be coherent and consistent (logical or otherwise), which (also) makes it independent of thought (Ansichsein).
For something whatsoever to be moreover  a  real  genuine being ("real" in the sense of HARTMANN), it must be, in addition to the just mentioned conditions, fully determined as to its qualitative content, and moreover resting on a formless substrate effecting it to be in principle repeatable, i.e. it must be an individuum, which in turn means that it stands under specific here-and-now conditions, which ultimately make it physical and dynamic. As such it is the product of one or another here-and-now dynamical system. And this product remains dynamical in character, continually interacting with other such products.
The full qualitative determinedness of such a real being consists of a complete stack of partial whatnesses, like symmetry and promorph (which exist -- in the Real -- realiter, but are not beings themselves, while they are so in the Ideal Sphere), together making up the full intrinsic content, which is the full and phenotypically manifest what-is-it of a given real being. While these partial whatnesses just statically constitute the overall whatness, the latter -- and also the former -- is generated and sustained by the fully physically interpreted dynamical law of the corresponding dynamical system, and this dynamical law is the genotypical or ultimate whatness of the given real being, effecting the phenotypical manifestation of its properties. Further, as has been said, all this qualitative content rests on a formless substate, which makes it repeatable over several instances. And as such it is, moreover, constantly subjected to, and perturbed by, extrinsic agents, resulting in accidental features falling onto it, that mask the intrinsic content (the what-is-it) of that real being.
Indeed, it is this being embedded within a dynamical context, externally and internally, which makes it a true real being, and distinguishes it from it to be merely an ideal being (in HARTMANN's sense).
So all these general conditions together make up the metaphysical layering, a layering that as such pervades every genuine real being in the same general way, and which has been expounded in more detail in all the forgoing of the present document.
Each non-concrete layer of a real being exists realiter in the Real and idealiter in the Ideal. So the same what-is-it aspect can have two different ways-of-being-there, realiter and idealiter.
But of course there are many coherent structures or patterns in the Ideal Sphere that are not materialized in the Real at all, because the latter's overall dependency web does not admit such structures to pervade the whole of the Real. Some of them could, however, occur in remote or more or less hidden and isolated corners of the Real, and could be discovered by Natural Science.

Above we referred to another type of layering of the Real, namely a layering that expresses a more or less discrete increase in material complexity. This layering is not of a metaphysical character, and does not, as a whole system of layers, cut across every individual being of the Real, because some inhabitants of the Real are much more complex than others in that Sphere.
Today, there is much speculation about the so-called emergent properties resulting from complex dynamical systems. The 'emergent' status of these properties is not, however, ontological in character. They do not come out of the blue. They are merely unexpected and unpredicted, so their 'emergence' is of an epistemological nature. They were already contained in the relevant dynamical system, albeit implicitly so. They are the unfoldings of (previous enfoldings in) its physically determined dynamical law. Such unfoldings often manifest themselves as more or less abrupt increases in material complexity and as such show the way how something like the human mind can emerge from a complex dynamical system. But all this addresses the problem (or question) whether dynamical systems, and indeed evolution itself, actually do represent an increase in complexity (or in fact do not), because as has been said, this complexity was already, in a sense, present in the system anyway. It demands special investigations about the nature of the mentioned implicitness, and thus of the nature of emergence. The theory of David BOHM's Implicate Order answers this question :  All the complexities are already present, but initially enfolded within the Implicate Order. And there is a constant process of unfolding and enfolding going on, from the Implicate Order to the Explicate Order and back again, a dynamics in, so to say, the vertical direction, while the resulting horizontal sequence, visible in the Explicate Order, suggests a physical horizontal process. Describing and explaining the latter process, as Natural Science does, is, however, according to BOHM, only an approximation to the real process that takes place.
As has been related earlier, this theory is expounded in the Third Part of my website, and according to me is interesting (especially because its doctrinal ties with the metaphysics  of  PLOTINUS ), but speculative.
For the time being we could stick to the current scientific paradigm that complexity is truly increasing during the course of dynamical systems, and evolution in general, and that the degree of implicitness of those subsequently emerging structures and properties within the physically interpreted dynamical law is very high indeed, and that, moreover, this implicitness and the subsequent explicitness is of a purely physical nature, without different Orders being involved within the Real Sphere of being. The transition from being implicit in the physical dynamical law to being explicit should then be considered as a causal process, i.e. a physical generation. But, the degree being high or low, the implicitness, as being something physical, strongly underlines the ontological homogeneity of the Real Sphere.

So with all this we have set the symmetry groups into a general ontological context, clarifying their existential status, and increasing our understanding of the most significant aspect  of  STRUCTURE :  SYMMETRY.
In addition to that we have introduced the PROMORPH, which constitutes a further specification (and reference) toward the Real Sphere of existence. It goes beyond symmetry down into further domains of the STRUCTURE of material objects.
In the Real Sphere symmetry is not actually generated by the symmetry group, which is only its what-is-it, but by certain dynamical systems. The same goes for the promorph.
In the Ideal Sphere there is no generation at all. The symmetry groups just exist there idealiter as coherent timeless structures (when interpreted mathematically), and their status is intermediate between the Ideal and the Real, when interpreted physically but still being general. The corresponding abstract group as such exists in the very Ideal Sphere of being. Finally, the promorphs as promorphs are intermediate between the Ideal and the Real, while the corresponding geometric solids, as just geometric solids, exist in the Ideal Sphere of being.

If one wants to continue the line of ontological research as outlined in this INTERMEZZO (instead of continuing the present Group Theory Series), Click HERE  ( Fourth Part of Website).

e-mail : 

back to homepage

Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology

Back to subpatterns and subgroups (introduction)

Back to subpatterns and subgroups Part II

Back to subpatterns and subgroups Part III

Back to subpatterns and subgroups Part IV

Back to subpatterns and subgroups Part V

Back to subpatterns and subgroups Part VI

Back to subpatterns and subgroups Part VII

Back to subpatterns and subgroups Part VIII

Back to subpatterns and subgroups Part IX

Back to subpatterns and subgroups Part X

Back to subpatterns and subgroups Part XI

Back to subpatterns and subgroups Part XII