
e-mail :

Sequel to Group Theory
As always, we start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite two-dimensional periodic patterns, or Ornaments (sequel)
In the previous document we considered the antisymmetry derivable from the plane group P2mg and the subgroups of that group not necessarily associated with antisymmetry or color symmetry. Here we will show some (other) examples of antisymmetry patterns derivable from that group, and, in addition, such examples as found in ancient ornamental art.

Figure 1. Antisymmetry pattern with the antisymmetry group P2mg / Pg .
(Adapted from JABLAN, 2002)
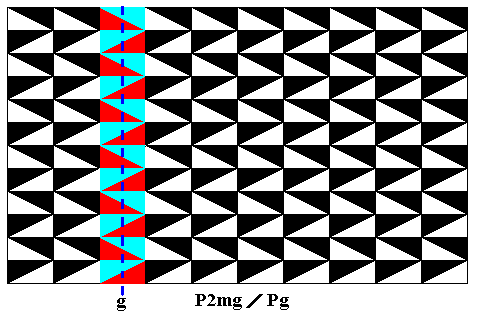
Figure 2. Same pattern as in previous Figure.
One type of glide line ( g ) of the pattern highlighted. Compare with Figure 19 of Part XVI.

Figure 3. Same pattern as in previous Figure.
The other type of glide line ( g ) of the pattern highlighted. Compare with Figure 19 of Part XVI.
The next Figure gives an example of an antisymmetry patttern with antisymmetry group P2mg / Pg from ancient ornamental art.

Figure 4. Antisymmetry ornament P2mg / Pg from Neolithic art.
(Adapted from JABLAN, 2002)
The next Figure gives an example of an antisymmetry patttern with antisymmetry group P2mg / Pm from ancient ornamental art.
Figure 5. Antisymmetry ornament P2mg / Pm from Neolithic art.
(Adapted from JABLAN, 2002)

Figure 6. Pattern representing the generating symmetry group P2mg of the antisymmetry ornament P2mg / Pm depicted in the previous Figure (Neolithic art).
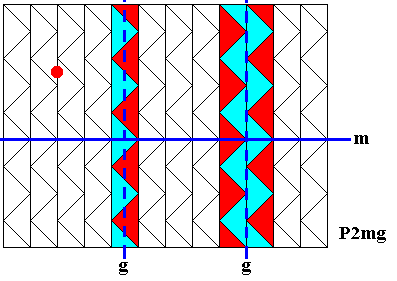
Figure 7. Analysis of the pattern representing the generating symmetry group P2mg of the antisymmetry ornament P2mg / Pm depicted in Figure 5 (Neolithic art).
Two types of glide lines (g), one mirror line (m) and a half-turn (red dot) are indicated.
The pattern must be imagined to be extended indefinitely over the plane.
This concludes our investigation of antisymmetry and subgroups of the plane group P2mg.

Figure 8. Pattern representing the plane group P2gg . The group elements are represented by the yellow and green areas. A unit mesh (blue) is indicated.
We will now derive antisymmetry patterns from the above P2gg ornament. In doing so we set the initial background color to be blue, and interpret the antiidentity transformation e1 as the color permutation (Red Blue) (cycle notation). This permutation then relates exclusively to the background color.
Figure 9. The initial background color of the P2gg pattern of the previous Figure is set to be blue. One area is chosen to represent the identity element 1 .
The next Figure indicates the generating glide reflections that can generate all group elements from the identity element.
Figure 10. The symmetry elements (glide lines, indicated by dashed lines) of the two generating glide reflections. They can generate all group elements, and thus from the area representing the identity element (they can generate) the whole P2gg pattern.
The next four Figures show that these two glide reflections can generate the whole P2gg pattern.

Figure 11. First of all the two glide reflections generate all the group elements (and thus the corresponding areas representing those elements) lying on the glide lines themselves.
From the elements of the horizontal (glide) line we can generate other elements by subjecting them to the vertical glide reflection, as shown.
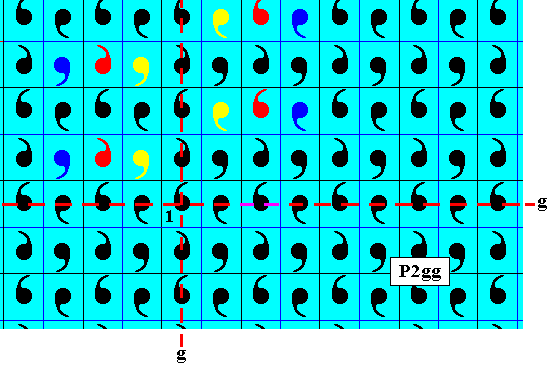
Figure 12. From the newly generated elements we can generate still more elements by subjecting them in turn, and repeatedly, to the vertical glide reflection.
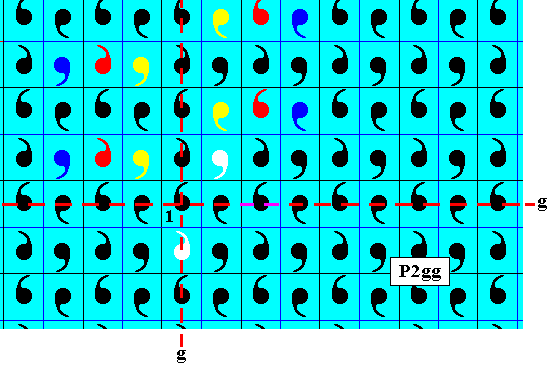
Figure 13. Here it is shown how already generated elements lying on the vertical glide line will generate still more elements when subjected to the horizontal glide reflection (white colored commas).

Figure 14. If we subject the identity element (1) to the horizontal glide reflection, resulting in the area with the red comma, and then subject this result to the vertical glide reflection, we end up with the upper left (area with a) green comma. So the two green commas represent the combined horizontal and vertical glide reflection. And these green commas clearly are related to each other by a half-turn (indicated by the small solid blue ellipse). Thus we see that the two perpendicular glide reflections imply a half-turn.
We can therefore conclude that these two glide reflections are sufficient to generate the whole pattern and constitute a possible generator set.
A first antisymmetry pattern will be derived by replacing the generating horizontal glide reflection gh by the antisymmetry transformation e1gh . The next Figure gives the result.
Figure 15. Antisymmetry pattern P2gg / Pg derived from the P2gg pattern of Figure 9, by replacing the generating horizontal glide reflection by its corresponding antisymmetry transformation.
The next Figures explain the above derivation of the antisymmetry pattern. For every new stage the newly generated red elements are, for the time being, given as purple, or directly as red elements, while the newly generated blue elements are, for the time being, given as green elements.

Figure 15a. The horizontal generating glide reflection + e1 ( = e1gh) creates (starting from the [area representing the] identity element) the color alternation as given in this Figure. The vertical glide reflection does not alter the original color of the identity element. The two generating glide reflections are indicated by dashed lines.
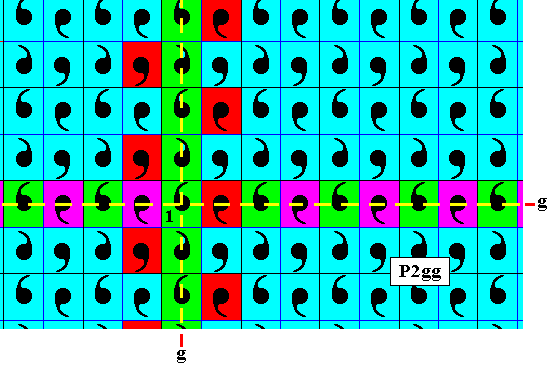
Figure 15b. From the element just to the right of the identity element the vertical generating glide reflection does not effect color aternations. The newly created elements are given as red.
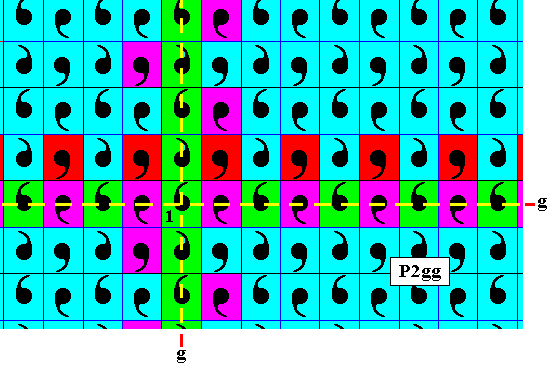
Figure 15c. The red element bordering at the upper-left corner of the identity element generates a horizontal series of red elements as indicated (because a horizontal translation does not effect a color change).
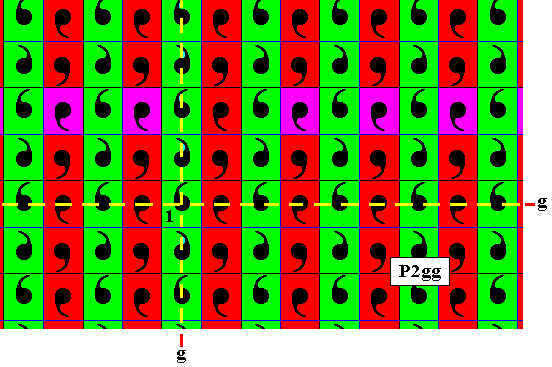
Figure 15d. All the remaining effects of the (repeated) horizontal translation (which as such does not effect a color change) are now filled in, resulting in the antisymmetry pattern of Figure 15 (when having set for green : blue, and for purple : red).
In Figure 15 we can see that the set of blue elements (containing the identity element) forms a subgroup representing Pg symmetry, because it consists of a vertical generating glide line and a horizontal generating translation. See next Figure.

Figure 16. Subgroup associated with the antisymmetry group represented by the pattern of Figure 15. This subgroup has Pg symmetry (vertical generating glide reflection and horizontal generating translation) [ The vertical generating glide line passes through a vertical row of commas].
Compare with Figure 2 of Part XIV, where we see a horizontal generating glide line and a vertical generating translation (In this image the group elements are indicated by rectangular areas, whereas in the present image they are not so indicated [which is in the present context immaterial]. In both cases a lattice mesh contains two commas related to each other by a glide line).
Because the involved subgroup has Pg symmetry, the symbol for the above derived antisymmetry group (Figure 15) must read P2gg / Pg .
The next two Figures show the respective point lattices of the generating P2gg pattern and the just derived antisymmetry pattern.

Figure 16a. Point lattice (indicated by red connection lines) of the generating P2gg pattern.

Figure 16b. Point lattice (indicated by yellow connection lines) of the above derived antisymmetry pattern. The unit mesh of the original generating P2gg pattern is indicated by dark blue lines and alternative colors. The extent of the unit mesh of the antisymmetry pattern is the same.
The next Figure gives the point lattice (indicated by dark blue connection lines) of the above derived antisymmetry pattern, without further auxiliary lines.

Figure 16c. Point lattice (indicated by dark blue connection lines) of the above derived antisymmetry pattern.
The next antisymmetry pattern can be obtained from the P2gg pattern of Figure 9 by replacing the horizontal generating translation th (which as such could belong to a possible generator set) by the corresponding antisymmetry transformation e1th , where the antiidentity transformation e1 is again the color permutation (Red Blue) (cycle notation), with respect to the background color. See next Figure.
Figure 17. Antisymmetry pattern, derived from the P2gg pattern of Figure 9 by replacing the generating horizontal translation by its corresponding antisymmetry transformation. As always, the pattern must be imagined to be extended indefinitely over the plane.
The next Figures explain the just derived antisymmetry pattern.
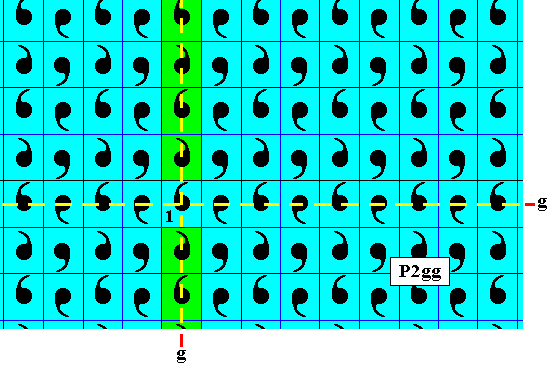
Figure 18. The vertical row (of areas representing group elements) going right through the (area representing the) identity element is generated by repeatedly applying the vertical generating glide reflection. So no horizontal translation is involved, and thus the colors of the elements of this row remain blue (indicated, for the time being, by green). The generating horizontal and vertical glide lines are indicated by dashed lines.
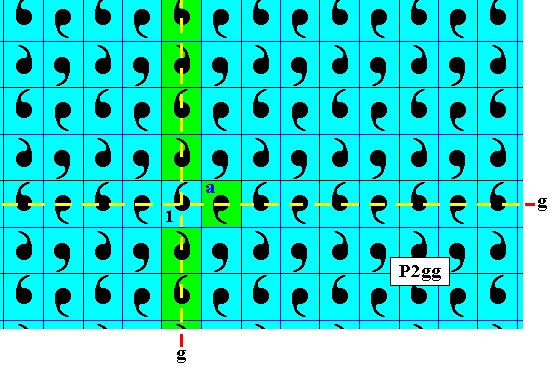
Figure 19. If we go from 1 to a no horizontal translation is involved -- we get there by the horizontal generating glide reflection -- and thus the initial color blue will remain blue (indicated, for the time being, by green).
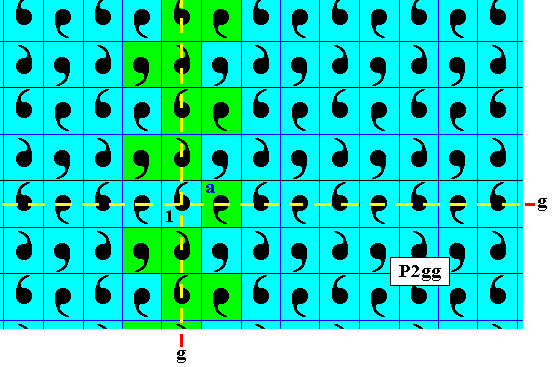
Figure 20. If we repeatedly subject a to the vertical generating glide reflection, still no horizontal translations are involved. So all the generated elements remain blue (indicated, for the time being, by green).
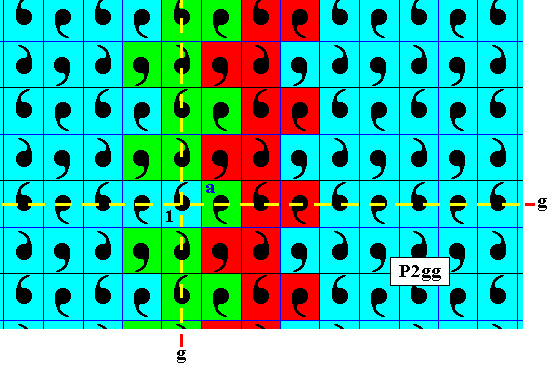
Figure 21. If we subject the identity element and all the already generated elements to one time the horizontal translation to the right -- which here means that we subject these elements to the antisymmetry transformation e1th -- the newly appearing elements must have their background color red.

Figure 22. If we subject the in the previous Figure newly generated elements (which are red) again to one time the antisymmetry transformation e1th -- the newly appearing elements must have their background color changed from red to blue (indicated, for the time being, by green).
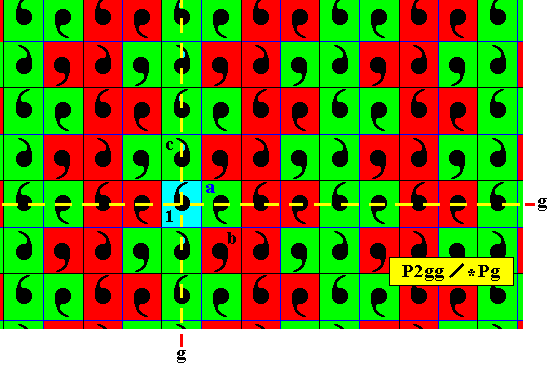
Figure 23. Subjecting the elements that newly appeared in Figure 20 repeatedly to the transformation e1th to the right and to the left -- and thus involving the transformations . . . th-2 ( = e1th-1e1th-1 ), e1th-1 , e1th , th2 ( = e1the1th ), e1th3 . . . -- will result in the color alternation as indicated (where th is the horizontal translation).
If we subject the element b to the horizontal glide reflection we get the element c , which has changed color with respect to b , which should, at first sight, not be so because the horizontal glide is just a symmetry transformation, not an antisymmetry transformation. We must, however, realize that the horizontal glide relection involves a horizontal translation (after every two times applying it), and thus involves the antisymmetry transformation e1th , and thus in turn involves a color change (See next Figures for further explanation).
If we now restore the green colors to blue, we indeed get the pattern of Figure 17, i.e. the antisymmetry pattern derived from the P2gg pattern of Figure 9. In the next Figures we have partially done this.

Figure 24. Action of the horizontal generating glide reflection on the elements m, k, i, h, g, f, e, d, n, o, p, q, etc. of the lower row (i.e. the lower of the two alternatively colored elements).

Figure 25. If we subject the element m of the lower row to the horizontal generating glide reflection, we obtain the element m of the upper row. And if we subject the latter element to this same glide reflection, we get the element i of the lower row. If we subject this latter element to that same glide reflection we get the element i of the upper row, etc.
Every two such consecutive glide reflections have the same effect as a horizontal translation. And indeed we see an alternation of colors, as was to be expected, because the horizontal translation is combined with the antiidentity transformation e1 , which causes the color alternation.
As we can see in the above Figure, m--m represents the horizontal glide reflection, while not involving a color change (as would be expected, because this glide reflection is just a symmetry transformation, not an antisymmetry transformation). But while m--i also represents this same glide relection, it involves a color change, from upper m to lower i as well as from lower m to lower i .

Figure 26. k--k represents the horizontal generating glide reflection and involves a color change. k--h also represents this glide reflection, but does not involve a color change. But k--k and k--h together form a horizontal translation and involve a color change (from lower k to lower h) , which was to be expected because the horizontal translation involves (as e1th) color change.
The next Figure gives our antisymmetry pattern after restoring all the remaining colors. It is the same pattern that was already depicted in Figure 17.
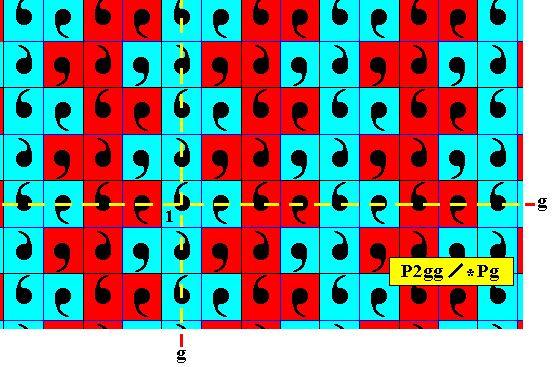
Figure 27. The just derived and analysed antisymmetry pattern with its proper colors. In this derivation the only symmetry transformation that was replaced by the corresponding antisymmetry transformation is the horizontal translation.
Let us we now isolate the blue elements of the just derived antisymmetry pattern.
Figure 28. Subpattern of blue elements of the above derived antisymmetry pattern. As will be shown below, the original horizontal glide line has disappeared.
Let's determine the status of the just given pattern consisting of the blue elements of the above derived antisymmetry pattern, especially as to whether it is a subgroup of the full (symmetry) group (Here the group P2gg) or not. Recall that a subgroup should first of all be a group. It must contain the identity element of the full group. Further one should be able to generate the subgroup using only symmetry transformations of the full group (P2gg).
Cases in which the set of elements still having the initial color, while being a subset of an antisymmetry group, but not a subgroup of this group, nor a subgroup of the generating symmetry group, are perhaps not reported in the literature. I myself have consulted only one technical book on the subject, namely JABLAN, S., 2002, Symmetry, Ornament and Modularity.
On page 30 JABLAN writes :
"Every junior antisymmetry group [with which category we are concerned] is uniquely defined by the generating group G and by its subgroup H of the index 2."This statement gives the impression that every junior -- i.e. e1 as such not belonging to the antisymmetry group, but only as combined with other transformations -- antisymmetry group implies one or another s u b g r o u p (of index 2, i.e. having half the number of elements of the full group). But our above case (and several more cases below) shows that this is not always so. Our antisymmetry pattern consists --as all antisymmetry patterns do -- of an equal number of blue (or whatever dual quality) elements (the color of all the elements of the generating symmetry group) and red elements. But in the present case this set of blue elements, although containg the identity element, and although forming a group, is not a subgroup of either the generating symmetry group or the derived antisymmetry group. And because our antisymmetry group is derived from its corresponding generating symmetry group (P2gg) by replacing only one symmetry transformation -- the horizontal translation -- by its corresponding antisymmetry transformation, we have to do with just a simple and regular case of antisymmetry, excluding any error in its derivation (In cases where more than one symmetry transformation is replaced by a corresponding antisymmetry transformation, we could expect interactions to occur leading to undetected errors). So our present antisymmetry case is a plain one, and we can be sure that this is indeed a case where no s u b g r o u p is implied by the antisymmetry, but only a s u b p a t t e r n , which has a symmetry according to one or another plane group.
We will now explore the above (Figure 28) found pattern of blue elements (which form a subset of the set of elements of the full group) as to its symmetry.
The next Figure shows that from the identity element -- marked as 1 -- we cannot generate the element directly to its right, because the horizontal glide reflection, needed to generate that element -- is, when repeatedly applied, bringing us outside the pattern (of blue elements), so we cannot use this transformation to generate that element.

Figure 29. The subpattern consisting of all the blue elements of the above derived antisymmetry pattern. The generating horizontal glide reflection (indicated by its symmetry element, the glide line) is, although a symmetry transformation of the full group (Figure 10 ), not a symmetry transformation of the group represented by our set of blue elements. The transformation brings us outside the pattern as indicated.
In fact in the previous Figure we found out that the element directly to the right of the identity element cannot belong to the pattern as a group, but it nevertheless does belong to the pattern. This means that in order for this pattern to be discussed as representing a group, the elements of this group must be differently conceived : The identity element, the element just to its right, and all other comparable areas representing alleged group elements, are not elements at all, i.e. not group elements of the pattern of blue elements considered as a group. We have to put two such 'elements' together, forming one element, and if we do so with respect to all other 'elements' of the pattern, we obtain true group elements related to each other in such a way as to form an algebraic structure according to the plane group Pg . The next Figures illustrate this.

Figure 30. Subpattern of the above derived antisymmetry pattern. It is a (plane) group with elements as indicated : each element consists of two commas and blue background. The original horizontal glide reflection is no longer present (i.e. although the motif units of the new identity element are related to each other by such a glide reflection, the latter is not a symmetry transformation of the whole pattrern (as depicted in the present Figure) anymore.
The next Figure depicts this same pattern but now with all other auxiliary lines removed.

Figure 31. Subpattern of the above derived antisymmetry pattern. All auxiliary lines removed. The (for this pattern) generating vertical glide reflection is indicated by its symmetry element (glide line, dashed line).
The next Figure shows the working of the generating vertical glide reflection.
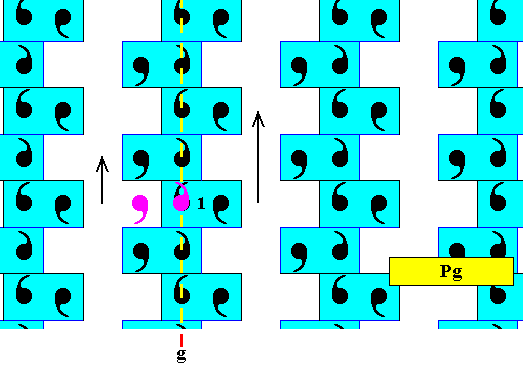
Figure 32. Subpattern of the above derived antisymmetry pattern. Explanation of the generating vertical glide reflection with respect to the identity element. The initial element (containing two commas as its motif s.str.) is reflected in the glide line (symbolized by the purple commas) and then translated upwards (by half a generating translation of the pattern, left arrow). The right arrow indicates the generating vertical translation of the present pattern.
As can be seen in the above Figure the symmetry of the pattern only consists of vertical glide lines and horizontal and vertical translations, and this is the finger print of the Plane group Pg .
The next Figure gives the point lattice of the subpattern under discussion.

Figure 33. Point lattice (indicated by connection lines) of the subpattern of the above derived antisymmetry pattern.
The next Figure, finally, shows that the vertical lattice lines coincide with vertical glide reflection lines in addition to those of which a representative was already found earlier.

Figure 34. Point lattice (indicated by connection lines) of the subpattern of the above derived antisymmetry pattern. All existing vertical glide lines are indicated.
In the above Figure we can see that a unit mesh contains three parallel glide lines and nothing more. So the pattern has indeed Pg symmetry.
The next three Figures depict the respective point lattices of the generating P2gg pattern and of the antisymmetry pattern derived from it earlier ( This antisymmetry pattern -- the implied subpattern of which was just discussed -- was depicted in Figure 17 ).

Figure 35. Point lattice (indicated by connection lines) of the generating P2gg pattern.

Figure 36. Indication of the point lattice (shown by yellow connection lines) of the above derived antisymmetry pattern (Figure 17 ). The pattern must be imagined to extend indefinitely over the plane. The unit mesh representing the point lattice of the original generating P2gg pattern is shown by dark blue lines and alternative coloring (red --> purple, blue --> green).
The Figure demonstrates that the unit mesh of the antisymmetry pattern, as given here, contains all morphological, orientational and chromatic features of that pattern : The commas of the original unit mesh, indicated by the symbols 1, a, b, d, are present, as well as their colored counterparts. The mesh is moreover periodically repeated all over the plane, and so constitutes a genuine unit mesh of the antisymmetry pattern, and as such representing its lattice.
The next Figure, finally, gives the point lattice (indicated by dark blue connection lines) of the antisymmetry pattern, without all other auxiliary lines.

Figure 37. Point lattice (indicated by dark blue lines) of the above derived antisymmetry pattern P2gg / Pg .
In the next document we will derive still more antisymmetry patterns from our initial P2gg pattern (Figure 9 ).
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology).
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV
Back to subpatterns and subgroups Part V
Back to subpatterns and subgroups Part VI
Back to subpatterns and subgroups Part VII
Back to subpatterns and subgroups Part VIII
Back to subpatterns and subgroups Part IX
Back to subpatterns and subgroups Part X
Back to subpatterns and subgroups Part XI
Back to subpatterns and subgroups Part XII
Back to subpatterns and subgroups Part XIII
Back to subpatterns and subgroups Part XIV
Back to subpatterns and subgroups Part XV
Back to subpatterns and subgroups Part XVI