2-D patterns XXVII

The Symmetry of Two-dimensional Patterns

As prelude to the symmetry of three-dimensional crystals and organisms

Subpatterns and Subgroups Part XXVII (Subgroups and Antisymmetry in Ornaments)

e-mail :

Sequel to Group Theory

As always, we start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.

Infinite two-dimensional periodic patterns, or Ornaments (sequel)

In the previous documents we analysed antisymmetry patterns as found in Neolithic art, and derivable from a C2mm pattern. Here we will give a final example from the same period.

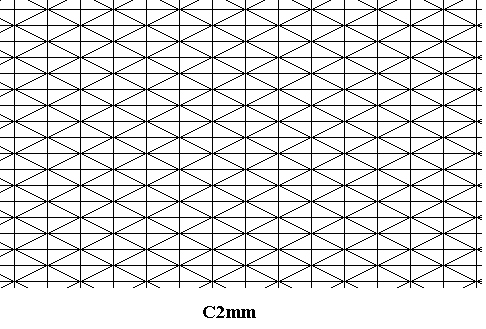
Figure 1. The generating C2mm symmetry pattern from which an antisymmetry pattern will be derived, found in Neolithic art.

The just depicted pattern belongs to the plane group C2mm. Having already extensively analysed a similar pattern with the same symmetry in the beginning of Part XXV of the present Series of documents, we can directly proceed to derive our neolithic antisymmetry pattern from it.

The neolithic antisymmetry pattern can be derived from the above generating C2mm symmetry pattern by replacing both generating reflections m_h and m_v and the SE translation t_se by their corresponding antisymmetry reflections e₁m_h and e₁m_v and e₁t_se , where the antiidentity transformation is interpreted as being the color permutation (White Black) (cycle notation) with respect to the color of the areas representing group elements (and at the same time being fundamental regions of the pattern). The initial color is set to be white.

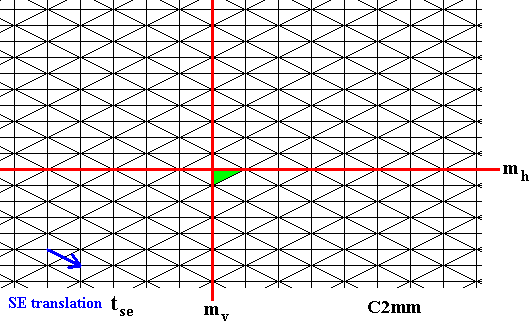
Figure 2. Possible generators of the pattern of Figure 1. The identity element is indicated (green). The right-angled triangles represent group elements and the fundamental region of the pattern. The generators are :
Reflection in the line m_h.
Reflection in the line m_v.
The South-East translation t_se (given by its vector -- blue arrow).

We will derive the antisymmetry pattern in several steps (Figure 3--24). The newly generated white elements will, for the time being, be colored blue, and later be restored to white.

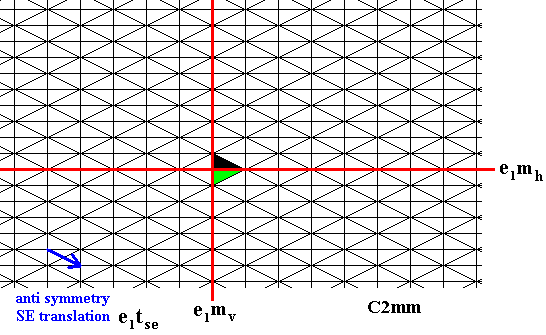
Figure 3. The identity element (which color is white, but here indicated by green) is reflected in the line m_h and involved a color change, because we have to do with the antisymmetry reflection e₁m_h .

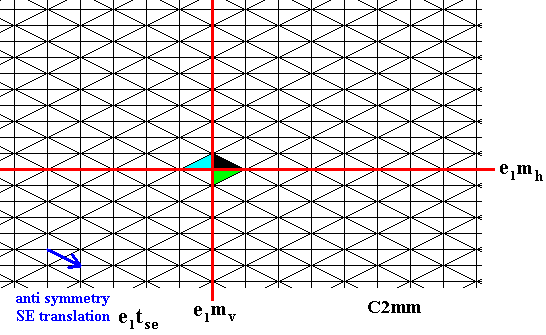
Figure 4. The black element generated above is subjected to the vertical antisymmetry reflection, e₁m_v , resulting in a color change (from black to white, here indicated as blue).

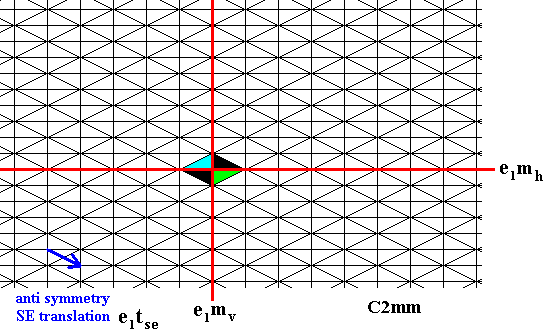
Figure 5. If we apply the vertical antisymmetry reflection to the identity element we get a new black element.

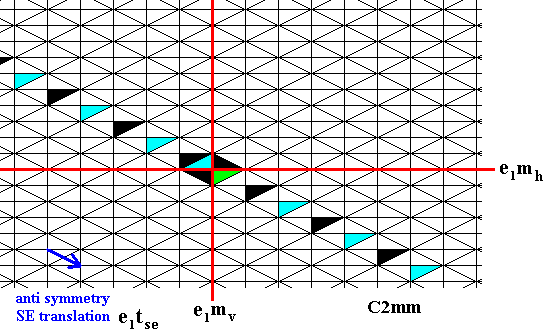
Figure 6. If we repeatedly apply the South-East antisymmwetry translation, e₁t_se , to the identity element, we get a color alternation in the SE direction, because (e₁t_se)²ⁿ = (t_se)²ⁿ (no color change), and (e₁t_se)²ⁿ⁺¹ = e₁(t_se)²ⁿ⁺¹ (color change).

If we do this also with the remaining three elements that were initially generated, we get the following :

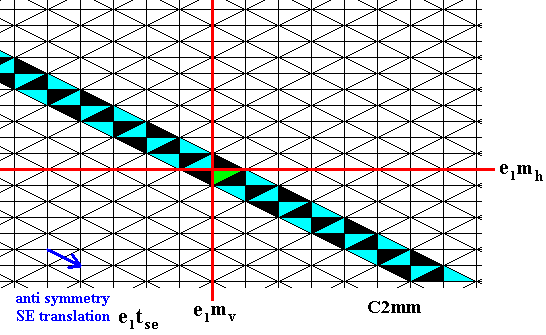
Figure 7. The elements of the rhombus, which were obtained earlier (Figure 5 ), are subjected to the SE antisymmetry translation, resulting in alternating colors along the SE direction in the pattern.

Of course the strip of elements, now obtained, extends indefinitely in both (opposite) directions. So when we apply the vertical antisymmetry reflection e₁m_v to this strip, the result will be another strip, extending indefinitely parallel to the NE diagonal in both (opposite) directions. See next Figures.

Applying the antisymmetry reflection to the elements already obtained involves a color change. We start by showing this for four new elements generated by this antisymmetry reflectio :

Figure 8. Generation of four new group elements by applying the antisymmetry reflection e₁m_v to already existing elements. For clarity we have colored the white elements among them yellow.

The next Figure does this with respect to the next four elements of the SE strip.

Figure 9. Generation of four new group elements by applying the antisymmetry reflection e₁m_v to already existing elements. For clarity we have colored the white elements among them yellow.

Again four new elements are generated by the application of the vertical antisymmetry reflection :

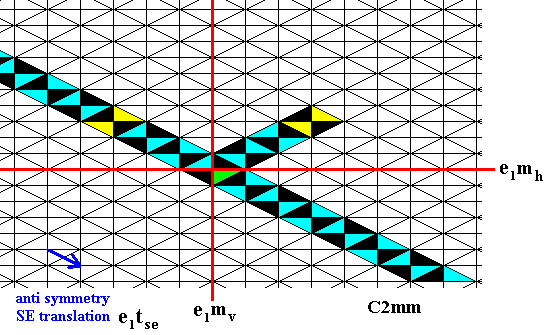
Figure 10. Generation of again four new group elements by applying the antisymmetry reflection e₁m_v to already existing elements. For clarity we have colored the white elements among them yellow.

The next Figures continue to generate more elements in this way :

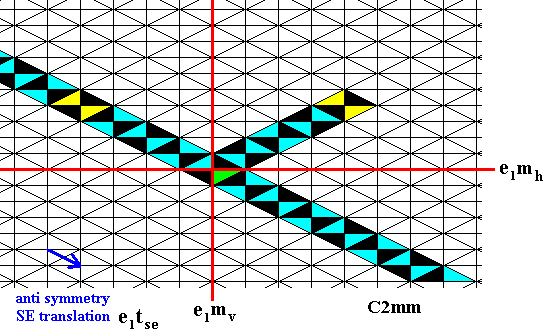
Figure 11.

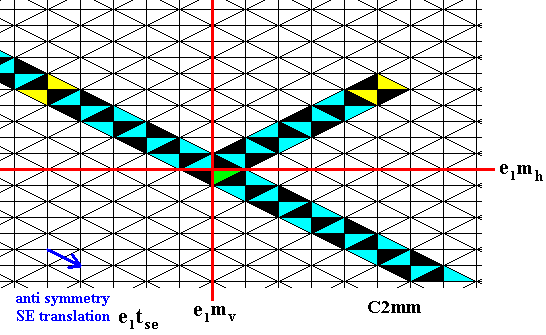
Figure 12.

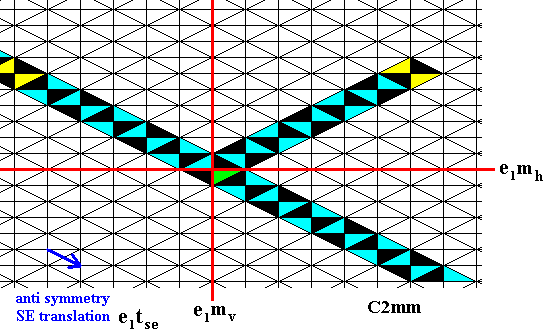
Figure 13.

Figure 14.

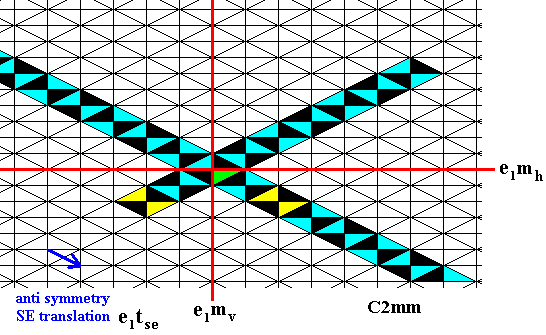
Figure 15.

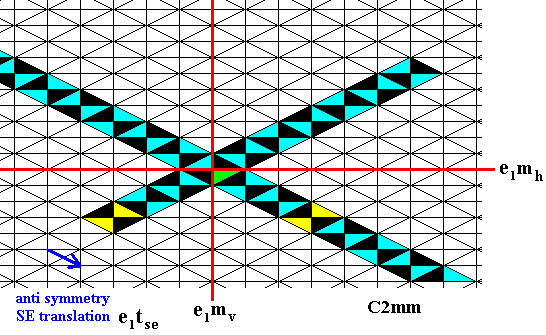
Figure 16.

Figure 17.

Figure 18.

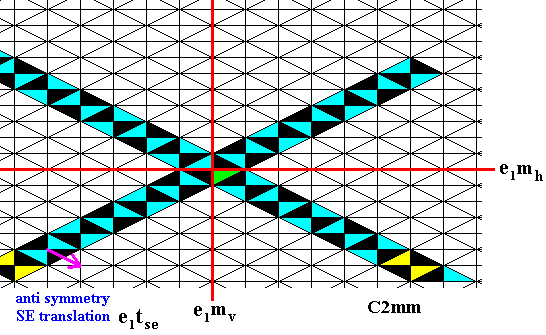
Figure 19.

Because the South-East row extends indefinitely in both opposite directions, the new North-East row, derived from it by the transformation e₁m_v , will also extend indefinitely in both opposite directions :

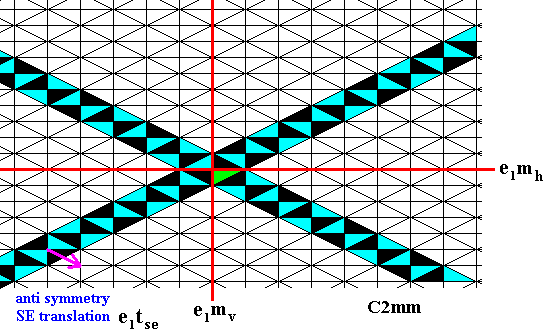
Figure 20.

Now we will derive new elements from the NE row by applying to its elements the SE antisymmetry translation e₁t_se repeatedly. This results in color alternation, because
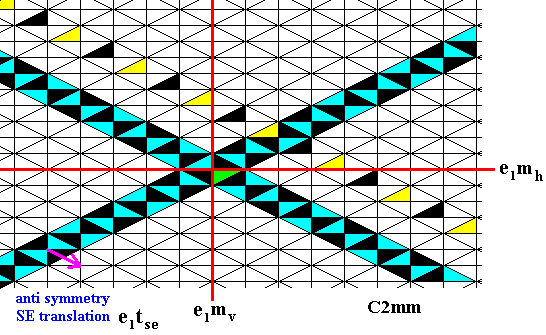
(e₁t_se)²ⁿ = (t_se)²ⁿ and (e₁t_se)²ⁿ⁺¹ = e₁(t_se)²ⁿ⁺¹ , where e₁ implies a color change. First we will show this for one element of the NE row, then for three more such elements, and finally for all the elements of the NE row (which extends indefinitly in both opposite directions). See next Figures.

Figure 21. generation of new elements by applying the SE antisymmetry translation to an element of the already generated NE row.

Figure 22. generation of more elements by applying the SE antisymmetry translation to three more elements of the already generated NE row.

By this procedure we can now generate all the remaining elements of the antisymmetry pattern (although this pattern is of course infinite) :

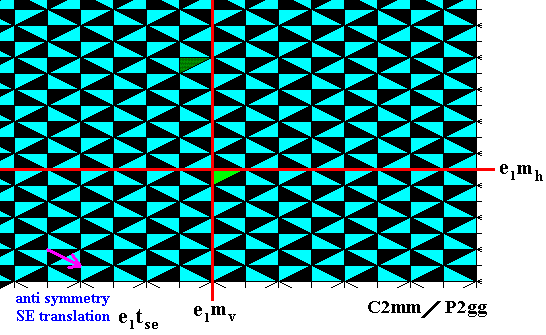
Figure 23. Final stage of the generation of the elements of the antisymmetry pattern.

Restoring the color blue to white, we get our neolithic antisymmetry pattern.

Figure 24. The neolithic antisymmetry ornament, as a result of the above derivation from the generating C2mm (Figure 1 ), by replacing the horizontal and vertical generating reflections and the generating SE translation by their corresponding antisymmetry transformations.

To identify the just derived antisymmetry ornament we isolate the subpattern of the white elements (containing the identity element), and see what its symmetry is :

Figure 25. Subpattern consisting of the white elements of the just derived antisymmetry ornament, as we see these elements in Figure 24. In the present and subsequent Figure we have colored these elements b l u e for clarity.

The next two Figures demonstrate the presence of vertical glide lines (one indicated) in the just derived subpattern :

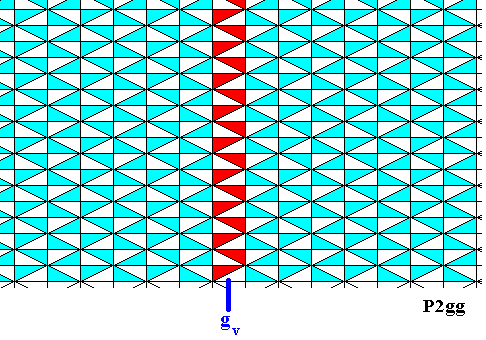
Figure 26. The just derived subpattern has vertical glide lines. One of them is highlighted.

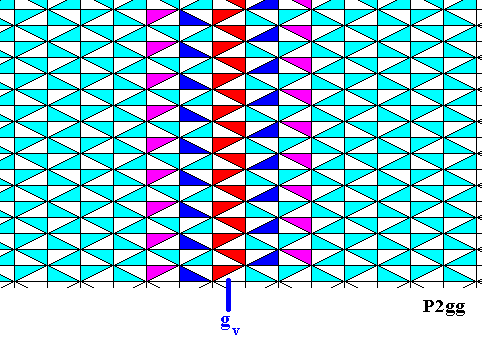
Figure 27. Further elucidation of the vertical glide line indicated in the previous Figure.

The subpattern has also horizontal glide lines. One of them is illustrated in the next Figure.

Figure 28. The just derived subpattern has also horizontal glide lines. One of them is highlighted.

The implied half-turns can easily be detected in the subpattern. The pattern has, however, no reflections whatsoever. And this means that the symmetry of our subpattern is according to the plane group P2gg . So the symbol for the above derived antisymmetry ornament (implying our subpattern) must read C2mm / P2gg .

The next two Figures show possible point lattices (displaced with respect to each other, but equivalent) of our subpattern (which represents the P2gg subgroup of the antisymmetry group representing the above derived antisymmetry ornament).

Figure 29. Primitive rectangular point lattice (indicated by red connection lines) of the subpattern derived above. A unit mesh is indicated by alternative colors.

Figure 30. Alternative, and equivalent, primitive rectangular point lattice (indicated by red connection lines) of the subpattern derived above. A unit mesh is indicated by alternative colors.

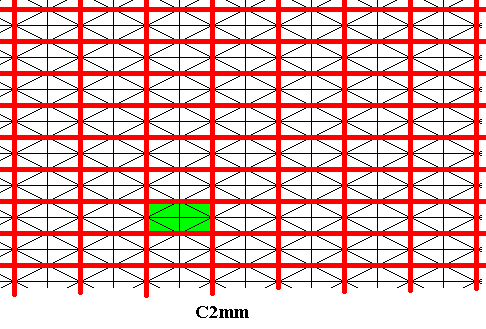
Figure 31. Primitive rectangular point lattice (indicated by red connection lines) of the generating C2mm symmetry pattern (Figure 1 ), from which the antisymmetry ornament was derived.

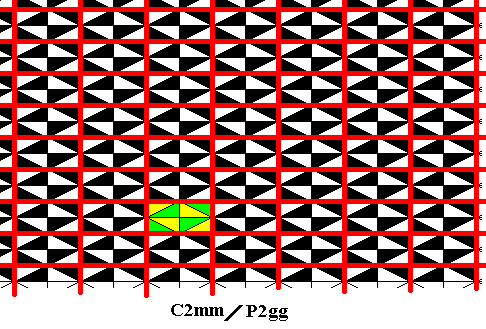
Figure 32. Primitive rectangular point lattice (indicated by red connection lines) of the antisymmetry ornament C2mm / P2gg (Figure 24 ). A unit cell is indicated by alternative colors.

This concludes our investigation of antisymmetry, subpatterns and subgroups of the plane group C2mm.
We will continue these studies for the remaining plane groups, and we recall that all this is still within the context of a group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic (3-D) symmetry of organisms (promorphology).

e-mail :

The next LINK will bring the reader to the Sequel to Contents of the present Series. Within this Sequel to Contents the reader can click to the next Part (of our present Series), namely Part XXVIII :
To continue click HERE

back to homepage

Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology

Back to subpatterns and subgroups (introduction)

Back to subpatterns and subgroups Part II

Back to subpatterns and subgroups Part III

Back to subpatterns and subgroups Part IV

Back to subpatterns and subgroups Part V

Back to subpatterns and subgroups Part VI

Back to subpatterns and subgroups Part VII

Back to subpatterns and subgroups Part VIII

Back to subpatterns and subgroups Part IX

Back to subpatterns and subgroups Part X