(Alternative names : Cubic System, Tesseral System, Regular System)
The Isometric crystal system characterizes itself by its three equivalent crystallographic axes perpendicular to each other. This means that undistorted crystals do not look elongated or flattened. They look like objects that could fit within a sphere.
The Isometric System comprises six Crystal Classes.
The empty building block, of all the crystals belonging to this system, has the shape of a cube, which implies that the symmetry (point symmetry) of the crystals belonging to the most symmetric Class, and means the Holohedric Division (of the Isometric System) is identical with the symmetry of a cube.
The concept of (basic) Form and the symbols (according to WEISS, according to NAUMANN and according to MILLER -- all three methods are equivalent) used for faces and Forms are expounded in the previous Essay which generally treats of The Morphology of Crystals.
For infinity (used as a possible index or coefficient in the symbols) we use the sign ~ in the text. In Figures we use the conventional symbol for infinity, namely a horizontal numeral eight.
| Division | Class | mirror planes |
axes | cs |
| Holohedric | Hexakisoctahedric 4/m 3* 2/m |
3 + 6 | three [4] four [3] six [2] |
+ |
| Tetrahedric Hemihedric |
Hexakistetrahedric 4* 3 m |
6 | three [2] four [3] p. |
- |
| Pentagonal Hemihedric |
Duakisdodecahedric 2/m 3* |
3 | three [2] four [3] |
+ |
| Plagihedric Hemihedric |
Pentagonikositetrahedric 4 3 2 |
- | three [4] four [3] six [2] |
- |
| Tetartohedric | Tetrahedric pentagondodecahedric 2 3 |
- | three [2] four [3] p. |
- |
We will now derive these five Symmetry Classes (Crystal Classes) of the Isometric Crystal System, starting with the highest symmetrical Class.
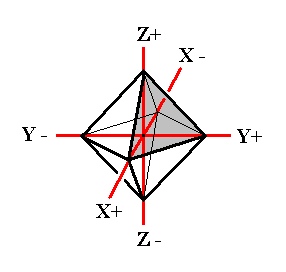
Figure 1. Basic Form (regular octahedron) of the Isometric Crystal System, and the set of crystallographic Isometric axes.
In this Figure we have drawn the basic Form of the Isometric Crystal System, the regular octahedron. One face is shaded, it is the unit face for the Isometric Crystal System. This face cuts off equal pieces of the three crystallographic axes, and can accordingly be denoted by a : a : a, in which the three a's express the fact that the three axes are equivalent.
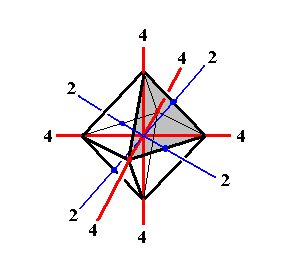
Figure 2. Some symmetry elements of the Cubic Hexakisoctahedral Class. Depicted : All three 4-fold rotation axes (4), and two (out of six) 2-fold rotation axes (2).
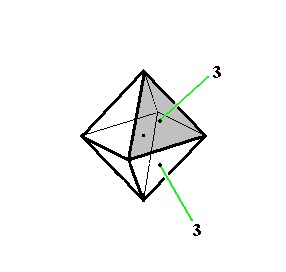
Figure 3. Some symmetry elements of the Cubic Hexakisoctahedral Class. Depicted : two (out of four) 3-fold rotatation axes (3).
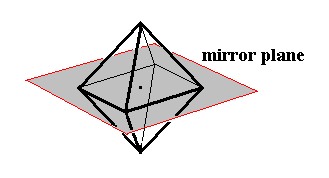
Figure 4. Some symmetry elements of the Cubic Hexakisoctahedral Class. Depicted : one (out of nine) mirror plane, and center of symmetry (represented by the dot in the middle of the image).
Now if we consider the shaded face in Figure 1 in isolation, i.e. if we think of having only this one face, then we can generate the complete Form (the regular octahedron of Figure 1) when we subject this face to all the symmetry elements (symmetry operations) belonging to our Crystal Class, here the Cubic Hexakisoctahedral Crystal Class (resulting in the finished form having all the symmetries of that Class) :
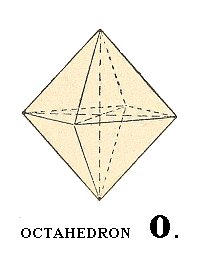
Figure 5. The Regular Octahedron.
Basic Form of the Hexakisoctahedral Class.
A next basic Form of this Class is the cube.
To accomplish its derivation we let the shaded face of Figure 1 become more and more steep, which means that the length of the cut-off piece of the Z-axis becomes bigger and bigger. In the limit this piece becomes infinitely long. The face has now aquired a vertical position. Next we turn this vertical face such that it becomes parallel to the X and Z axes (while remaning vertical). In this way we obtain the face of a cube (oriented correctly), namely its right vertical face, and this face can be denoted by : a : ~a : ~a.
If we now subject this vertical face to the symmetry elements of our Class then a cube will be generated : The vertical 4-fold rotation axis will result in the four vertical faces of the cube, and a secondary mirror plane (demanded to be present in the finished structure) stretching between diametrically opposite horizontal edges of the until now generated structure generates the top and bottom faces of the cube. The figure we thus have generated not only is a cube, but also one with a convenient orientation : The crystallographic axes still coincide (as in the case of the above generated octahedron, the basic Form) with 4-fold axes. The Weiss symbol for the cube (= regular hexahedron) is :
(a : ~a : ~a), the Naumann symbol is ~O~., and the Miller symbol is {100}.
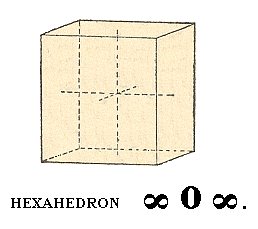
Figure 6. The Cube (Regular Hexahedron).
A next basic Form of this Class to be derived is the rhombic dodecahedron.
To accomplish this we let the shaded face of Figure 1 become vertical. This face can then accordingly be denoted by a : a : ~a. When we now subject this face to the symmetry elements of our Crystal Class we obtain a rhombic dodecahedron :
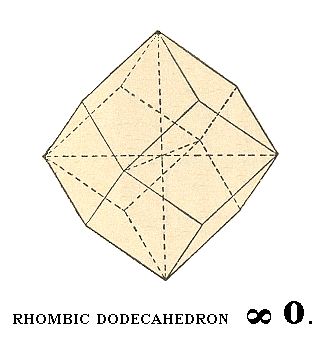
Figure 5. Another basic Form of the Cubic Hexakisoctahedral Crystal Class, the Rhombic Dodecahedron.
The Weiss symbol for this Form is accordingly : (a : a : ~a), the Naumann symbol is ~O., and the Miller symbol is {101}.
Another Form of this Class is the ikositetrahedron.
We can derive this Form as follows :
Starting again with the shaded face of the regular octahedron of Figure 1, we will let it turn horizontally such that the length of the cut-off piece of the Y-axis (i.e. the length of the piece cut off from the Y-axis by that face) has been increased, without having this increase carried to an extreme (meaning that the length of the cut-off piece does not become infinite). Many such positions of the face are possible, for example a case in which the cut-off piece of the Y-axis has become twice as long as the one of the X-axis. Here we will consider the general case, and say that the cut-off piece of the Y-axis has become m times as long as the one of the X-axis.
The symbol of the face would then read : a : ma : a. Next we are going to further subject the face a : ma : a to a turn such that the length of the cut-off piece of the Z-axis increases in precisely the same way as the cut-off piece of the Y-axis did before. The resulting face can then be described with the symbol : a : ma : ma.
If we now subject this face to all the symmetries of our Crystal Class, a polyhedron will be generated that is called an ikositetrahedron :
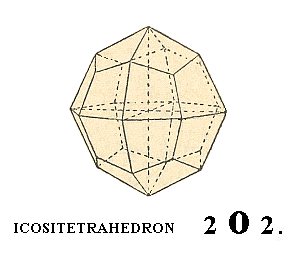
Figure 6. Yet another basic Form of the Cubic Hexakisoctahedral Crystal Class, the Ikositetrahedron.
The Weiss symbol for this Form is accordingly : (a : ma : ma), the Naumann symbol is mOm., and the Miller symbol is {hkk}.
In Figure we see an ikositetahedron for (the case of) m = 2.
The next Form is the Triakisoctahedron or pyramid octahedron :
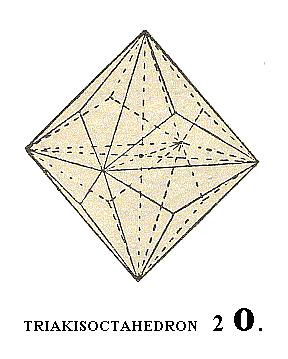
Figure 7. Another basic Form of the Cubic Hexakisoctahedral Crystal Class, the Triakisoctahedron.
The triakisoctahedron can be visualized as a regular octahedron with regular three-sided pyramids placed over the octahedron faces.
When we let the basic face of Figure 1 turn about its horizontal edge, i.e. let it become more steep, but not letting it become vertical, it cuts off a larger piece from the Z-axis, while the cut-off pieces of the other two axes remain unchanged. Such a face then can be symbolozed as
a : a : ma. When we now demand that this face is a part of a structure that is obedient to the symmetry of our Crystal Class, then we will obtain a triakisoctahedron.
The Weiss symbol signifying this Form will consequently be (a : a : ma), the Naumann symbol will be mO., while the Miller symbol reads {hhk}.
Figure 7 depicts a Triakisoctahedron for (the case of) m = 2.
The next Form is the tetrakishexahedron, or pyramid cube. It can be visualized as a cube with regular four-sided pyramids placed over its faces.
We can derive it by letting the basic face of Figure 1 turn about a vetical axis in such a way that the cut-off piece of the Y-axis increases (but not letting reach its limit) while the cut-off piece of the X-axis remains unchanged. We then obtain a face which can be symbolized as
a : na : ~a. Letting this face multiply according to the symmetry of our Class we obtain the tetrakishexahedron.
The Weiss symbol for this Form is accordingly (a : na : ~a), the Naumann symbol is ~On., and the Miller symbol is {hk0}.
In the Figure we see a tetrakishexahedron for (the case of) n = 2.
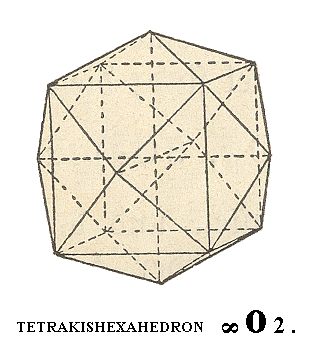
Figure 8. Another basic Form of the Cubic Hexakisoctahedral Crystal Class, the Tetrakishexahedron.
The last basic Form of the Cubic Hexakisoctahedral Crystal Class is the hexakisoctahedron, which is the most general Form, an d which gave the name for the Class.
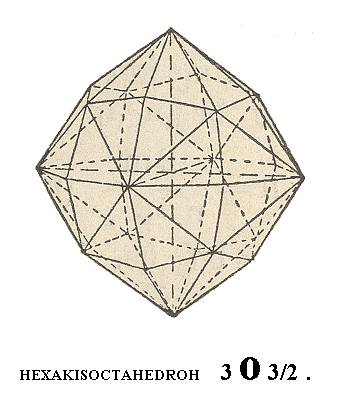
Figure 9. The most general Form of the Cubic Hexakisoctahedral Crystal Class, the Hexakisoctahedron. It possesses 48 faces.
To derive this Form we tilt the basic face of Figure 1 in the most general way, which means that we turn it to the effect that the cut-off pieces of the Y-axis and the Z-axis increase, but to an unequal extent, while the cut-off piece of the X-axis remains the same. The symbol for the resulting face then becomes a : na : ma. When we now multiply this face according to the symmetry of the Class we obtain a hexakisoctahedron.
The Weiss symbol for this Form is consequently (a : na : ma), the Naumann symbol is mOn, while the Miller symbol is {hkl}.
The one that is depicted in Figure 9 has m = 3, and n = 3/2.
Each of these described Forms can occur as a crystal (because they are closed), but also combinations of them can constitute crystal shapes. This is because they are all obedient to the same symmetry bundle (See Figure 10).
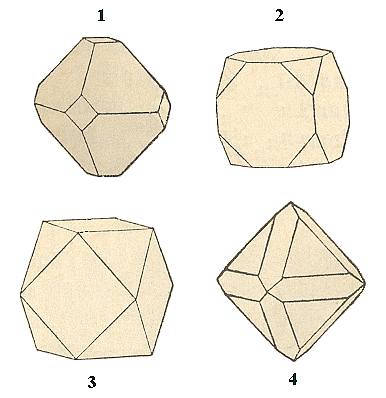
Figure 10. Some simple Combinations of Forms of the Cubic Hexakisoctahedral Class.
1. O.~O~. The corners of the octahedron are cut off by the cube.
2. ~O~.O. The corners of the cube are cut off by the octahedron.
3. Cuboctahedron. Equal development of cube and octahedron.
4. O.~O. The edges of the octahedron are cut off by the rhombic dodecahedron..
Often complicated combinations are encountered consisting of many faces.
As real representatives of the Cubic Hexakisoctahedral Class we could mention :
the minerals Copper Cu, Gold Au, Halite NaCl, and Fluorite CaF2.
To see the (larger) picture(s) click on the smaller one(s)
Fluorite - Val Sarentina (Italy). Crystals 5-15 mm.
This concludes our exposition of the Cubic Hexakisoctahedral Crystal Class.
This octahedron is divided into eight faces by the main mirror planes. When we drop those planes, half of these faces will disappear. When we then let the remaining faces extend we'll end up with a tetrahedron. In fact we can derive two such tetrahedra, depending on which set of octahedral faces is suppressed. See Figure 11.
Figure 11. The derivation of two correlate Forms (tetrahedra) from the holohedric octahedron.
1. Octahedron with its faces divided (by the main mirror planes) into two sets, each 'growing' into a tetrahedron.
2. Extension of the 'non-striped' faces of the octahedron (and suppression of the 'striped' faces).
3. Tetrahedron developed from the 'non-striped' faces of the octahedron.
4. Tetrahedron developed from the 'striped' faces of the octahedron.
These two tetrahedra, each bounded by four faces, are thus correlate Forms. They are congruent and are distinguished only by their orientation with respect to the crystallographic axes. This difference can be signified by a plus (+) or minus (-) sign. The faces of the tetrahedron are equilateral triangles. The line connecting the two upper corners is perpendicular to the line connecting the two lower corners. The orientation of all hemiedric Forms always corresponds (in drawings) with the one of the holohedric Form from which they are derived. So, in our case the crystallographic axes go through the middle of the edges of the tetrahedron, i.e. each axis connects two opposite edges by going through their mid-points.
We can symbolize such a tetrahedron as 1/2 (a : a : a). The Naumann symbol reads :
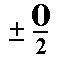and the Miller symbols are K{111} and K{11*1} (In fact the K is written as a greek letter, and 1* is written as a 1 with a horizontal score above it).
The cube, the rhombic dodecahedron and the tetrakishexahedron do not change their outer shape, because the suppressed mirror planes are perpendicular to the faces of these polyhedra, i.e. those planes, each for themselves do not separate two (symmetrical) faces (See Figures 12 and 13). So we could imagine that certain parts of the faces are removed because of the suppression of the (main) mirror planes, followed by an extension of the remaining parts, resulting in the suppressed parts being recovered again, which implies that the outer shape of the new Form has remained unchanged after all. However the crystallographic symmetry is lowered which means that for example the right upper corner at the front of a hemihedric cube behaves in a different way than the corresponding left corner does, when we investigate them physically.
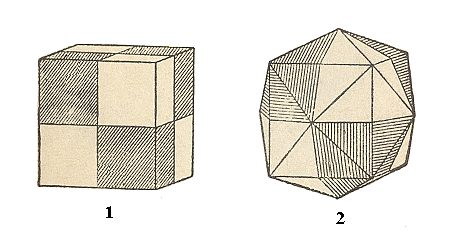
Figure 12. Cube (Hexahedron) and Tetrakishexahedron.
Their hemihedric Forms (the ones originating by the suppression of the main mirror planes of the holohedric Forms) retain the same geometrical shape as the corresponding holohedric Forms, but possess a lower symmetry than the latter.
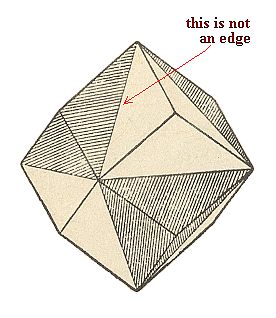
Figure 13. The hemihedric Form (the one originating by the suppression of the main mirror planes of the holohedric Form) of the Rhombic Dodecahedron has the same geometric shape as the corresponding holohedric Form but has a lower crystallographic symmetry.
The ikositetrahedron gives two trigondodecahedra (Singular : trigondodecahedron. For the plural we could also write : trigondodecahedrons) See Figure 14. These two Forms are congruent and are only distinguished from each other by their orientation with respect to the crystallographic axes.
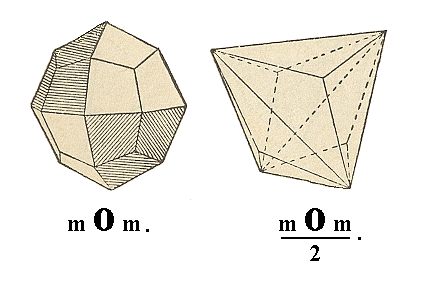
Figure 14. The unstriped faces of the Ikositetrahedron together make up a Trigondodecadedron (also called Pyramid Tetrahedron), another Form of the Hexakistetrahedric Crystal Class.
The Naumann symbol for this new Form, the trigondodecahedron, is
.
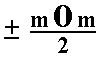The triakisoctahedron gives two deltoiddodecahedra, Forms, which are bounded by twelve deltoids, and which display a tetrahedral habit. See Figure 15.
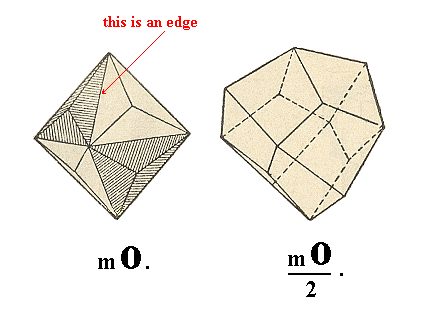
Figure 15. The unstriped faces of the Triakisoctahedron together form a Deltoiddodecahedron, yet another Form of the Hexakistetrahedric Crystal Class.
Finally the hexakisoctahedron (48-hedron) gives two hexakistetrahedra (24-hedra). This Form is bounded by unequilateral triangles, and has a tetrahedrical habit. See Figure 16.
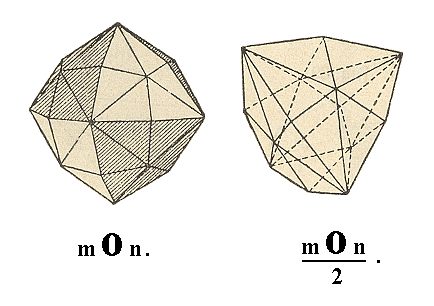
Figure 16. The unstriped faces of the Hexakisoctahedron together form a Hexakistetrahedron, the last Form of the Hexakistetrahedric Crystal Class.
These Forms can engage in all kinds of combinations with each other. Only Forms belonging to the same Crystal Class (Symmetry Class).
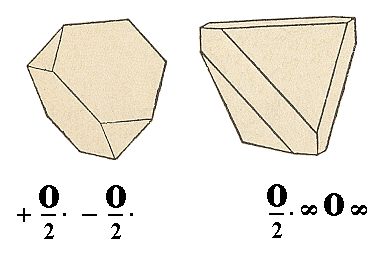
Figure 17. 1. A Tetrahedron with its corners cut off by the correlate Tetrahedron (the 'antitetrahedron'). When these two Tetrahedra were equally developed a Form would originate that looked like an Octahedron. But the difference of luster of the faces shows, in crystals where this is the case (For instance in the mineral Sphalerite, ZnS), generally easily betrays the fact that the Octahedron is not a simple Form but a combination.
2. The edges of the Tetrahedron are cut off by the Cube.
Remark : The symbol
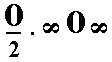should in fact be
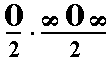. But in Forms that do not change their geometrical shape it is convenient not to emphasize their hemihedric character when this character is already evident by reason of their occurrence in combinations with other hemihedric Forms, that do change their shape and are accordingly explicitly symbolized as hemihedric Forms.
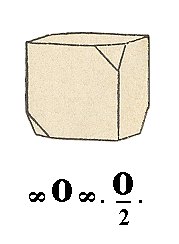
Figure 18. The alternate corners of the Cube are cut off by the Tetrahedron.
New Forms are generated by the tetrakishexahedron and the hexakisoctahedron.
The tetrakishexahedron gives two pentagondodecahedra. These are 12-hedra (i.e. polyhedra each consisting of twelve faces). Each one of these are bounded by symmetrical pentagons, i.e. of pentagons consisting of four equal sides and one having a deviating length. See Figure 19.
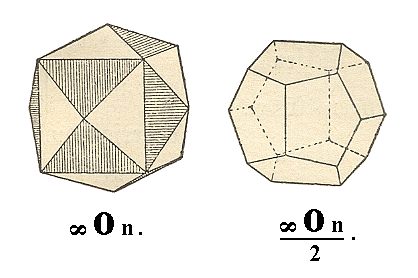
Figure 19. The unstriped faces of the Tetrakishexahedron together are going to constitute a Pentagondodecahedron, a new Form of the Dyakisdodecahedric Crystal Class.
The Miller symbols for this Form are p{h0k} and p{k0h} (in which the letter p is in fact (written by) the greek letter pi, signifying this type of hemihedric) . The Naumann symbol is given in the Figure.
The hexakisoctahedron gives two 24-hedra, dyakisdodecahedra, see Figure 20.
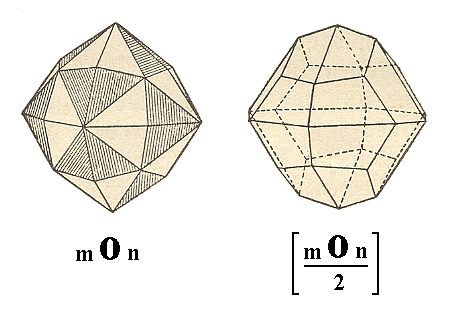
Figure 20. The unstriped faces of the hexakisoctahedron together are going to constitute a Dyakisdodecahedron, the last Form of the Dyakisdodecahedric Crystal Class. The large brackets of the Naumann symbol for the Dyakisdodecahedron are meant to distinguish this Form from the Hexakistetrahedron (Figure 16).
Also the Forms of this Class can engage in combinations, see Figure 21.
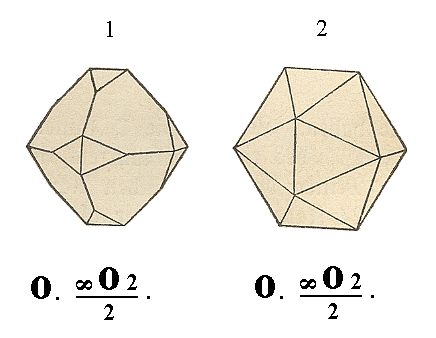
Figure 21. 1. The corners of the octahedron are each sharpened by two faces of the Pentagondodecahedron.
2. The same Form, but with both constituent Forms equally developed. It is a 20-hedron (i.e. consisting of 20 faces) in which the equilateral tiangles belong to the octahedron, while the isosceles triangles belong to the Pentagondodecahedron.
Yet another combination we see in the next Figure.
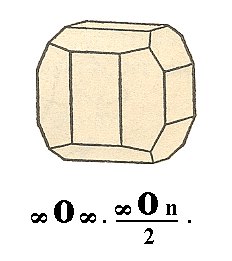
Figure 22. The edges of the Cube are obliquely cut off by the Pentagondodecahedron.
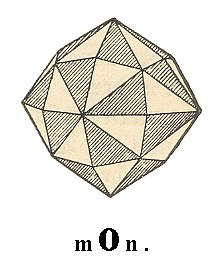
Figure 23. The unstriped faces of the hexakisoctahedron together are going to make up the Pentagonikositetrahedron 1 of Figure 24, while the striped faces are going to make up the Pentagonikositetrahedron 2 of Figure 24. These are new Forms of the Plagihedric Hemihedric Division. They are enantiomorphous.
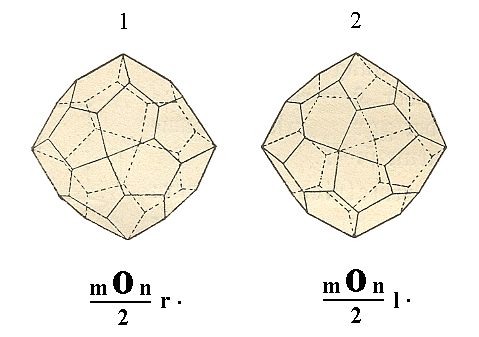
Figure 24. The two enantiomorphous Forms, Pentagonikositetrahedra, derived from the hexakisoctahedron.
The two correlate Forms of the pentagonikositetrahedron, are, in contradistinction to the hemihedric Forms treated so far, not congruent, but (plane) symmetrical with respect to each other, which means that they cannot be transformed into each other by any mechanical operation like rotation. They can only be transformed into each other by a reflection in a plane, like a right and left hand do. They are called enantiomorphous Forms and are signified as right-handed and left-handed respectively.
Their Naumann symbols are respectively
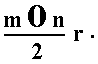and 
,
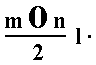and the Miller symbols are g{hlk} and g{hkl} (in which g is normally denoted by the greek letter gamma standing for gyros (curved), and meaning the gyrohedric hemihedric (= plagihedric hemihedric)).
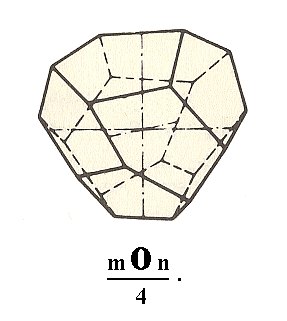
Figure 25. Tetrahedric Pentagon-dodecahedron, derived from the Hexakisoctahedron by applying first a pentagonal hemihedric, and then, to the result, a tetrahedric hemihedric.
When we proceed analogously with the remaining basic Forms of the Holohedric Division, we will derive
All these Forms, including the new Form (the tetrahedric pentagondodecahedron), can engage in combinations.
This concludes our exposition of the Isometric Crystal System.
The next System to be discussed is the Tetragonal Crystal System.