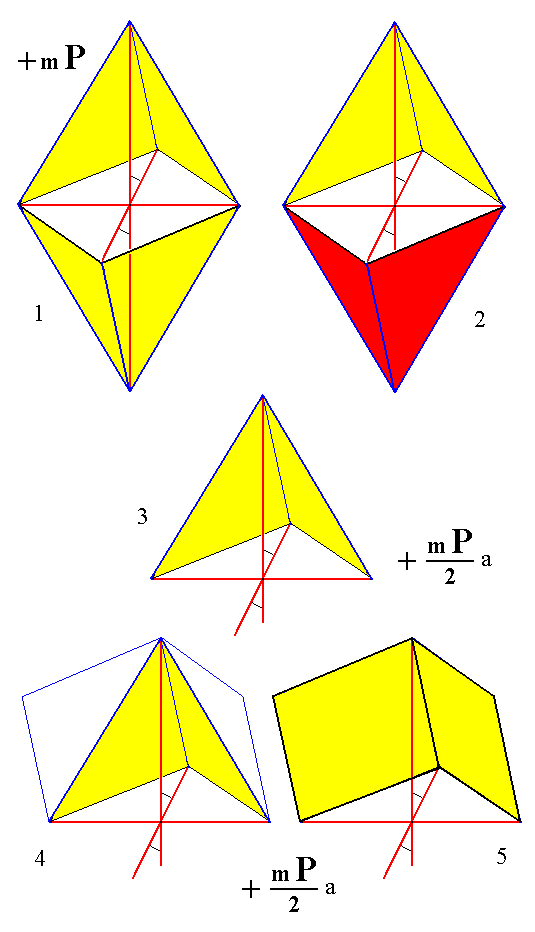
The Monoclinic Crystal System (Part Three) 



(Alternative name : Monosymmetric System)
back to homepage

back to Part One

back to Part Two

The Monoclinic-domatic Class
(= Hemihedric Division)   m

The symmetry elements of this Class are the folowing : The Forms of this Class are derived from the holohedric Forms by appying hemihedric to them which in this case means that the center of symmetry is suppressed. The 2-fold rotation axis will then dissapear by implication. The only symmetry element that remains is a mirror plane.
If a face configuration has a center of symmetry then this means that each face of such a configuration has a corresponding parallel counter face exactly opposite to it (opposite) with respect to the center of that configuration. Suppression of the center of symmetry implies the suppression of those counter faces. So the number of faces will be halved which is in fact a hemihedric (i.e. the application of hemihedric to that configuration). In the present Class the suppression of counter faces must be such that the mirror plane is retained. So, for example, in the case of the holohedric clinopinacoid we have two parallel faces. Suppression of the center of symmetry cannot in this case be accomplished by suppressing one of the faces because then also the mirror plane will disappear. So when this form of hemihedric is applied to the clinopinacoid it will retain its external shape, i.e. the resulting hemihedric Form will still consist of two parallel faces and so still having a mirror plane, but the faces are not such anymore that they stand in relation to each other according to a center of symmetry (the Form will not have a center of symmetry, which (absence) can be detected by the relevant physical behavior).

Recall from Part One that the holohedric Forms were the following :

Generalized Monoclinic Protohemipyramid.
Generalized Monoclinic Clinohemipyramid.
Generalized Monoclinic Orthohemipyramid.
Monoclinic Protoprism.
Generalized Monoclinic Clinoprism.
Generalized Monoclinic Orthoprism.
Generalized Monoclinic Clinodome.
Generalized Monoclinic Orthohemidome.
Monoclinic Clinopinacoid.
Monoclinic Orthopinacoid.
Monoclinic Basic Pinacoid.

MEROHEDRIC APPROACH

We shall derive the Forms of the present Class, the Monoclinic-domatic Class (= Hemihedric Division of the Monoclinic Crystal System) by subjecting the listed holohedric Forms one by one to hemihedric, which -- as has been said -- here means that the center of symmetry is suppressed.

From the holohedric monoclinic protohemipyramid can be derived a monoclinic hemihedric prototetartopyramid (= monoclinic dome) by subjecting it to hemihedric, i.e. by suppressing the center of symmetry. The holohedric hemipyramid decays into two independent halves, each of which consists of just two faces, either the two upper faces or the two lower ones. The next Figure depicts such a new Form consisting of the two upper faces.

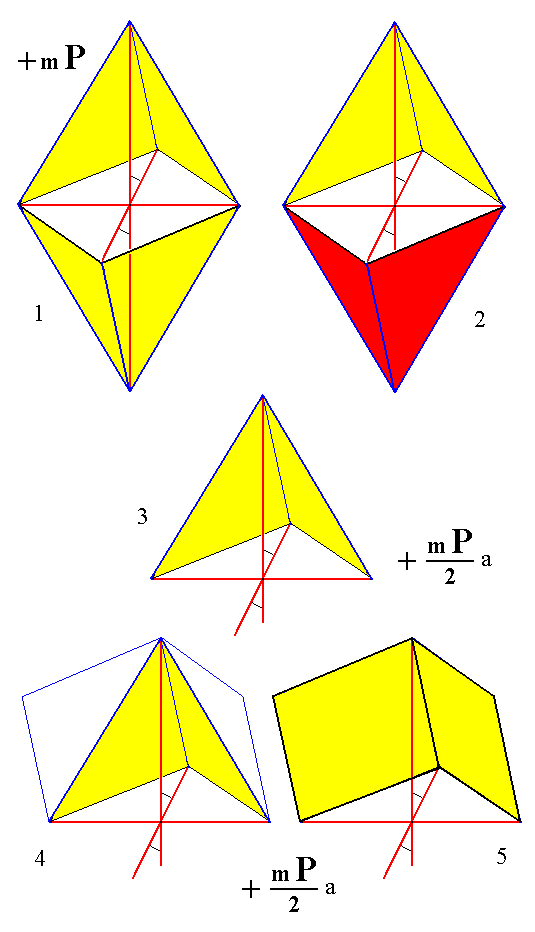
Figure 1.
(1). The holohedric (derived) positive Protohemipyramid.
(2). Indication of the suppression of faces in order to accomplish the loss of the center of symmetry.
(3). A possible resulting Form, in this case consisting of the upper two faces of the hemipyramid.
The sign "2" in the Naumann symbol indicates that hemihedric has been applied.
The sign "a" in the Naumann symbol means derived from upper faces.
(4). Extension of the faces of the Prototetartopyramid -- which does not change the Form crystallographically -- in order to show that it is in fact a dome.
(5). The resulting shape.
A second possible Form consists of the lower two faces of the hemipyramid.
In the same way two hemihedric Forms can be derived from the negative hemipyramid (See Figure 1a).
The crystallographic axes are depicted as red lines.
In (3), (4) and (5) it is clearly visible that the mirror plane is preserved.

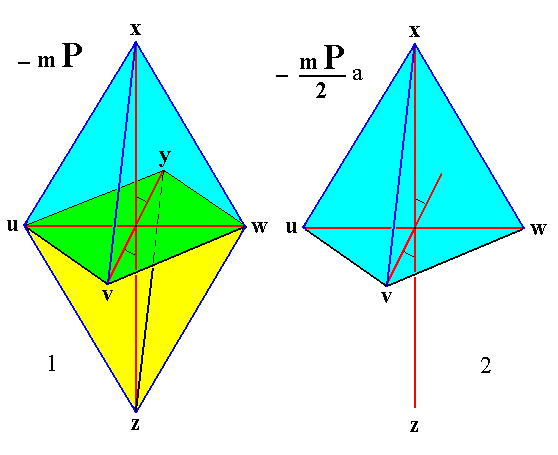
Figure 1a.
(1). The holohedric (derived) negative Protohemipyramid, consisting of four faces, two upper faces [uvx] and [vwx], and two lower faces [uyz] and [ywz].
(2). The hemihedric (derived) negative Prototetartopyramid ( = Monoclinoc Dome) consisting of the upper two faces of the holohedric hemipyramid.
The sign "a" in the Naumann symbol means derived from upper faces.
Yet another such Form can be derived consisting of the lower two faces of the negative holohedric hemipyramid.
From the holohedric monoclinic clinohemipyramid can, in the same way, be derived the hemihedric monoclinic clinotetartopyramid (= monoclinic dome) when subjected to hemihedric. See Figure 2.

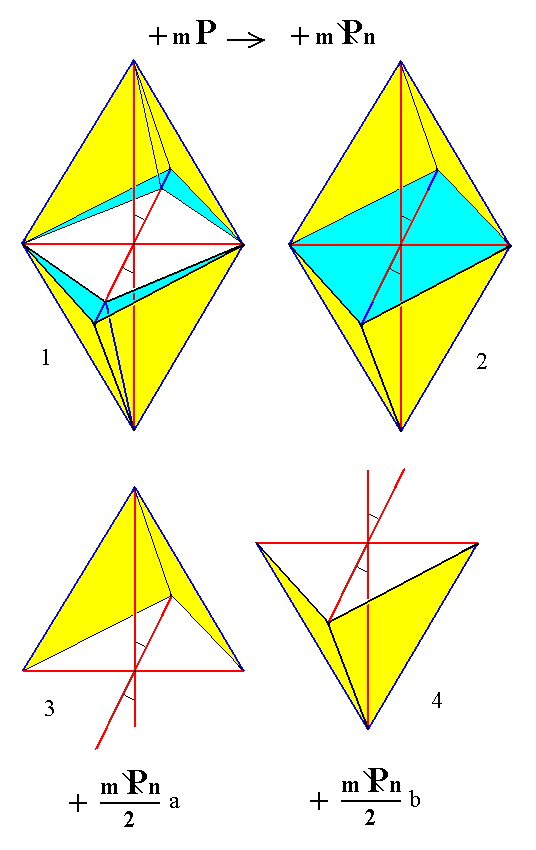
Figure 2.
(1). Derivation of the holohedric (derived, positive) Clinohemipyramid from the holohedric (derived, positive) Protohemipyramid.
(2). The resulting Clinohemipyramid, consisting of four faces (yellow).
(3). Derivation of a hemihedric Clinotetartopyramid from the upper faces of the holohedric Clinohemipyramid.
(4). Derivation of a hemihedric Clinotetartopyramid from the lower faces of the holohedric Clinohemipyramid.
The sign "a" in the Naumann symbol means derived from upper faces.
The sign "b" in the Naumann symbol means derived from lower faces.
In the same way we can derive hemihedric Clinotetartopyramids from the corresponding negative holohedric Clinohemipyramids.
From the holohedric monoclinic orthohemipyramid can, in the same way, be derived the hemihedric monoclinic orthotetartopyramid (= monoclinic dome) when subjected to hemihedric. See Figure 3.

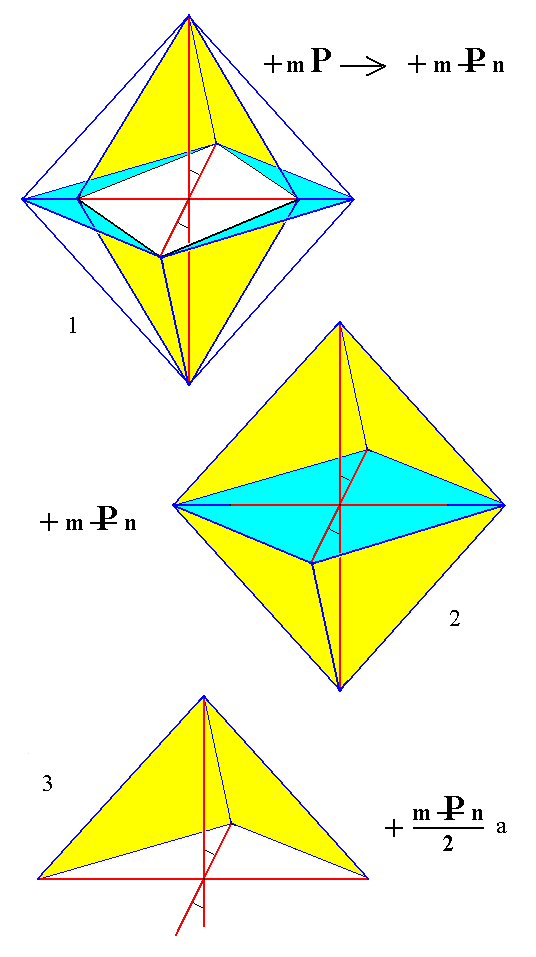
Figure 3.
(1). Derivation of the holohedric (derived, positive) Orthohemipyramid from the corresponding holohedric Protohemipyramid.
(2). The holohedric (derived, positive) Orthohemipyramid.
(3). Derivation of the hemihedric (derived, positive) Orthotetartopyramid from the upper faces of the hemipyramid.
Also from the lower faces can such a tetartopyramid be derived
In the same way such tetartopyramids can be derived from the corresponding negative Orthohemipyramid.
From the holohedric monoclinic protoprism can be derived the hemihedric monoclinic protohemiprism when subjected to hemihedric. This Hemiprism consists of two non-parallel vertical faces. See Figure 4.

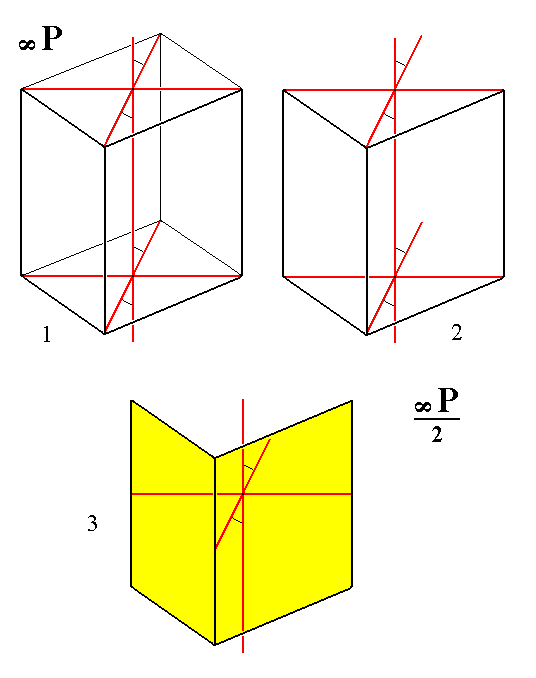
Figure 4.
(1). The holohedric Monoclinic Protoprism.
The axial directions are indicated by red lines.
(2). Derivation of the hemihedric Monoclinic Protohemiprism from the front faces of the Protoprism.
(3). The hemihedric Protohemiprism.
System of crystallographic axes in the center of the hemiprism. It is clearly visible that the mirror plane is still present.
Another such hemihedric hemiprism can be derived from the back faces of the Protoprism.
From the holohedric monoclinic clinoprism can, in the same way, be derived the hemihedric monoclinic clinohemiprism when subjected to hemihedric. See Figure 5.

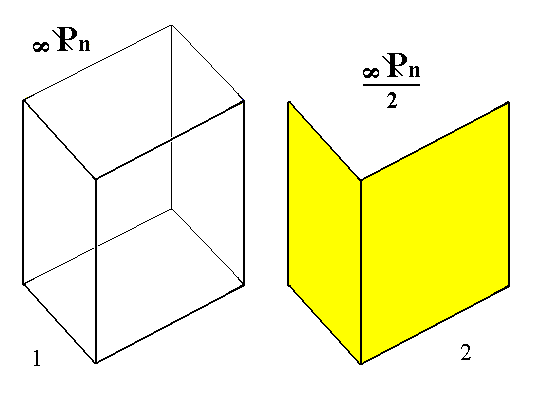
Figure 5.
(1). The holohedric Monoclinic Clinoprism.
(2). The hemihedric Monoclinic Clinohemiprism, derived from the front faces of the holohedric Clinoprism.
A second Form can be derived from the back faces of the holohedric Clinoprism.
From the holohedric monoclinic orthoprism can, in the same way, be derived the hemihedric monoclinic orthohemiprism when subjected to hemihedric. See Figure 6.

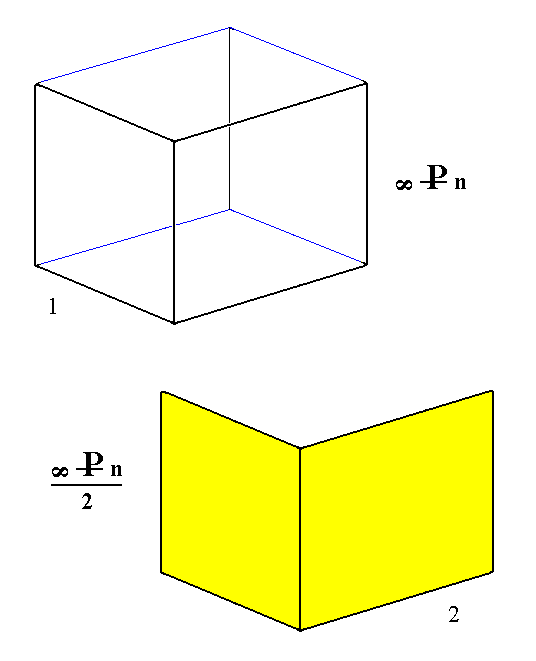
Figure 6.
(1). The holohedric Monoclinic Orthoprism.
(2). The hemihedric Monoclinic Orthohemiprism, derived from the front faces of the orthoprism.
A second Form can be derived from the back faces of the orthoprism.
From the holohedric monoclinic clinodome can be derived the monoclinic clinohemidome when subjected to hemihedric. The Holohedric Clinodome then decays into two independent halves, clinohemidomes, an upper one and a lower one.

Remark : It does not decay into a left half and a right half, because then not only the center of symmetry disappears but also the mirror plane (containing the clino and vertical axes), which would make the symmetry of the new Form inconsistent with that of our Class. See Figure 7.

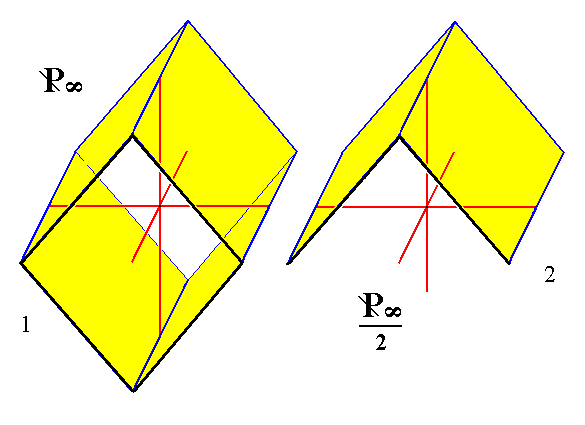
Figure 7.
(1). The holohedric ( primary, i.e. with m equal to 1 ) Clinodome.
(2). A hemihedric (primary) Clinohemidome, derived from the upper faces of the clinodome.
A second Form can be derived from the lower faces of the clinodome.
Of course the non-primary ( i.e. with m unequal to 1 ) Clinodomes give rise to the corresponding non-primary Clinohemidomes.
From the holohedric monoclinic orthohemidome can be derived the monoclinic orthotetartodome when it is subjected to hemihedric. The holohedric orthohemidome, which consists of two faces parallel to the ortho axis, then decays into two independent halves, each consisting of just a single face. See Figure 8.

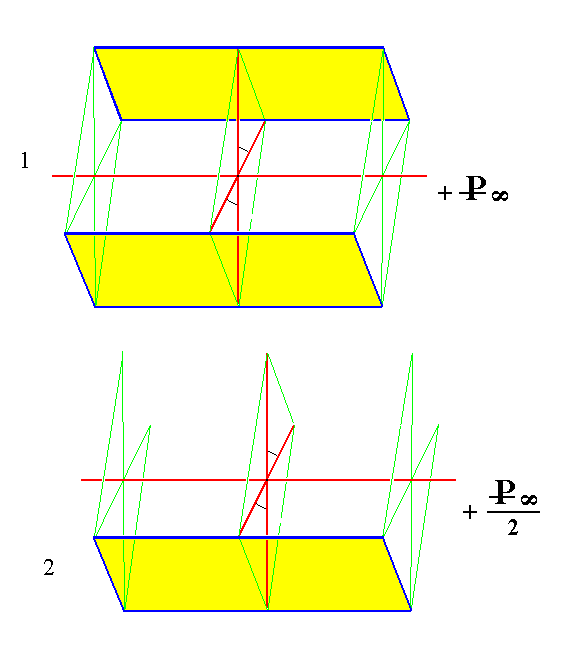
Figure 8.
(1). The holohedric (positive, primary) Monoclinic Orthohemidome.
(2). The hemihedric (positive, primary) Monoclinic Orthotetartodome, derived from the lower face of the holohedric Orthohemidome.
A second such tetartodome can be derived from the upper face of the Orthohemidome.
In the same way such tetartodomes can be derived from the negative Orthohemidome (See Figure 8a).
Of course the non-primary ( i.e. with m unequal to 1 ) Orthohemidomes give rise to the corresponding non-primary Tetartodomes.

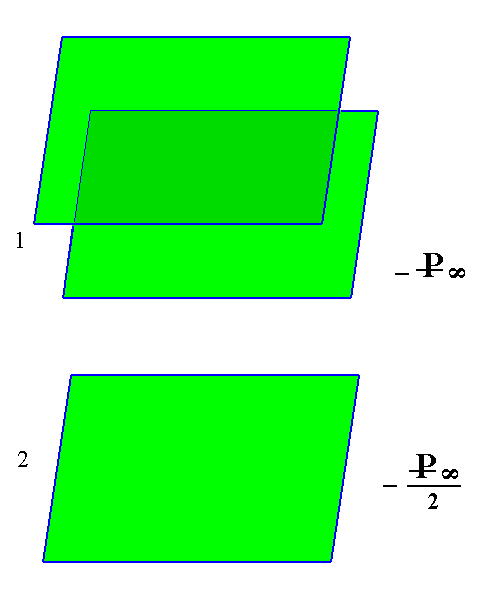
Figure 8a.
(1). The holohedric Monoclinic negative (primary) Orthohemidome. It consists of two faces parallel to the ortho axis and cutting the vertical axis at unit distances.
(2). The hemihedric Monoclinic negative (primary) Orthotetartodome, derived from the upper face (which intersects the vertical axis in its positive, i.e. upper, half) of the negative Orthohemidome. A second Form can be derived from the lower face of such a hemidome, i.e. from the face that intersects the vertical axis in its negative, i.e. lower, half.
Of course the non-primary Orthohemidomes yield the corresponding non-primary Orthotetartodomes.
From the holohedric monoclinic clinopinacoid can be derived the hemihedric monoclinic clinopinacoid when subjected to hemihedric. The external shape does not change, but the symmetry is lowered by the loss of the center of symmetry. So our new Form consists of two faces parallel to the clino and vertical axes. See Figure 9.

   
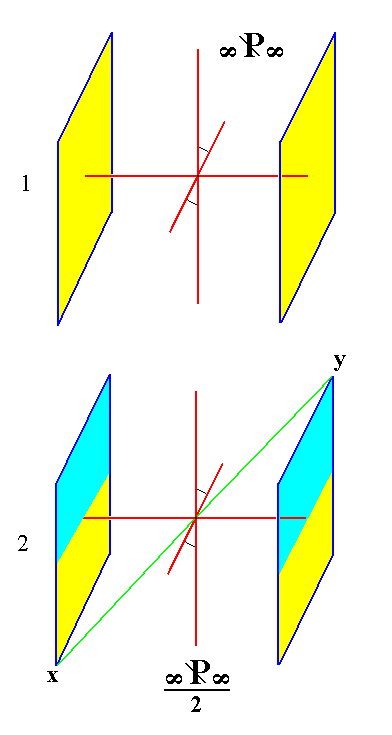Figure 9.
(1). The holohedric Monoclinic Clinopinacoid.
(2). The hemihedric Monoclinic Clinopinacoid.
The coloring indicates that the center of symmetry is suppressed (evident for example by the fact that x is not equivalent to y), but the mirror plane is still present. So indeed the resulting Form is compatible with the symmetry of the present Crystal Class.
From the holohedric monoclinic orthopinacoid can be derived the monoclinic orthohemipinacoid when hemihedric is applied to it. The holohedric orthopinacoid then decays into two independent halves each one of which consists of a single face parallel to the ortho and vertical axes. See Figure 10.

   
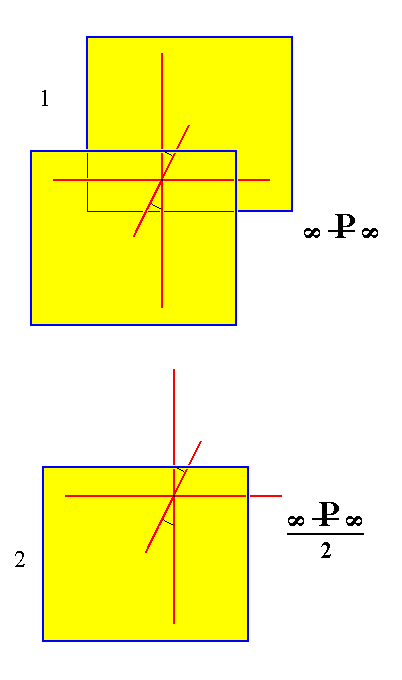Figure 10.
(1). The holohedric Monoclinic Orthopinacoid.
(2). The hemihedric Monoclinic Orthohemipinacoid, derived from the front face of the holohedric Orthopinacoid.
The center of symmetry is suppressed, but the mirror plane is still present.
A second Form can be derived from the back face of the holohedric Orthopinacoid.
From the holohedric monoclinic basic pinacoid can be derived the hemihedric monoclinic basic hemipinacoid (= hemihedric Monoclinic Pedion) when it is subjected to hemihedric. The holohedric Form then decays into two independent halves (Pedions), an upper one and a lower one. See Figure 11.

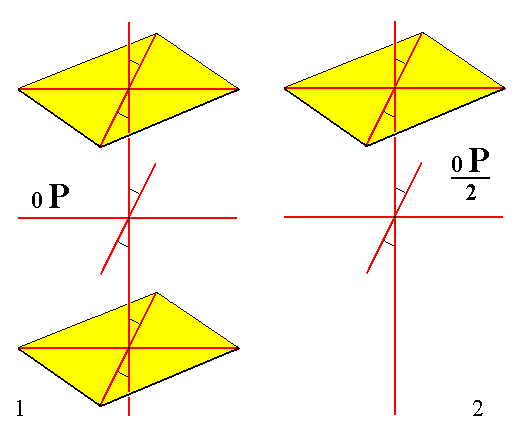
Figure 11.
(1). The holohedric Monoclinic Basic Pinacoid, consisting of two faces parallel to the clino and ortho axes.
(2). The hemihedric Monoclinic Basic Hemipinacoid (= hemihedric Monoclinic Pedion), derived from the upper face of the holohedric Basic Pinacoid.
The center of symmetry is suppressed, but the mirror plane is still present.
A second Form can be derived from the lower face of the holohedric Basic Pinacoid.
This concludes our derivation of all the Forms of the Monoclinic-domatic Crystal Class, by means of the merohedric approach.

All these Forms can (and, in this case must) enter in combinations with each other in real crystals.
FACIAL APPROACH

We will now derive those same Forms from the basic faces compatible with the Monoclinic Crystal System, by subjecting these faces one by one to the symmetry elements of the present Class. The only symmetry element of this Class is a vertical mirror plane, parallel to the clino axis. The derivations will be shown by means of stereographic projections.
Recall from Part One that the basic faces were the following :

a : b : mc
na : b : mc
a : nb : mc
a : b : ~c
na : b : ~c
a : nb : ~c
~a : b : mc
a : ~b : mc
~a : b : ~ c
a : ~b : ~c
~a : ~b : c

The stereographic projection of the symmetry elements of the present Class and of all the faces of the most general Form (a monoclinic dome) is given in the next Figure. Also the projections of the piercing points of the clino axis, i.e. the projections -- onto the projection plane -- of the points of intersection of the clino axis with the projection sphere, are given (Recall that the clino axis is not horizontal but tilted by the angle beta. This angle varies with the substance that is crystallized, and so does the location of the piercing points). See for further explanation of the stereographic projection of monoclinic crystals Part One.

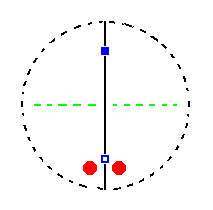  Figure 12.
Stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class, and of all the faces of the most general Form. There is one mirror plane (indicated by a solid line) as being the only symmetry element of the Class.
The projection of the piercing points of the clino axis
( =   a   axis ) is given in blue : the lower piercing point is represented by an open square, the upper piercing point by a solid square.
The face a : b : mc generates a monoclinic prototetartopyramid (= monoclinic dome) when subjected to the symmetry elements (in our case only one mirror plane) of the present Class :   The face is duplicated by the action of the mirror plane resulting in a face pair making up a monoclinic dome. See Figure 13.

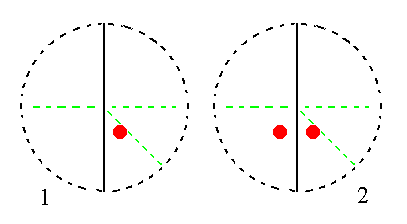
Figure 13.
(1). Position of the face a : b : mc in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is reflected in the mirror plane resulting in a Monoclinic Dome.
[The fact that for the face a : b : mc the projection of its face pole onto the projection plane does not lie on the bisector of the relevant quadrant of the projection plane is explained in Part One at the corresponding location in the text, and also in that same text after Figure 25.].
The face na : b : mc generates a monoclinic clinotetartopyramid (= monoclinic dome) when subjected to the symmetry elements of the present Class :   The face is duplicated by the mirror plane resulting in a monoclinic dome. See Figure 14.

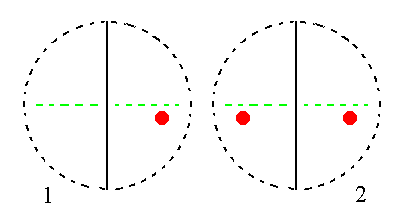  Figure 14.
(1). Position of the face na : b : mc in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is reflected in the mirror plane resulting in a Monoclinic Dome.
The face a : nb : mc generates a monoclinic orthotetartopyramid (= monoclinic dome) when subjected to the symmetry elements of the present Class :   The face is duplicated by the mirror plane resulting in a dome. See Figure 15.

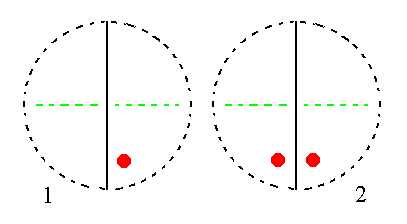  Figure 15.
(1). Position of the face a : nb : mc in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is reflected in the mirror plane resulting in a Monoclinic Dome.
The face a : b : ~c is vertical. It generates the hemihedric monoclinic protohemiprism when subjected to the symmetry elements of the present Class :   The face is duplicated by the mirror plane resulting in two vertical faces, a hemiprism. See Figure 16.

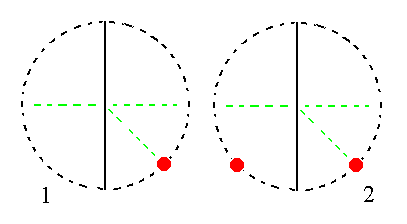  Figure 16.
(1). Position of the face a : b : ~c in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is reflected in the mirror plane resulting in a Monoclinic Hemiprism.
The face na : b : ~c is also vertical. It generates a hemihedric monoclinic clinohemiprism when subjected to the symmetry elements of the present Class :   The face is duplicated by the mirror plane resulting in a vertical face pair making up the hemiprism. See Figure 17.

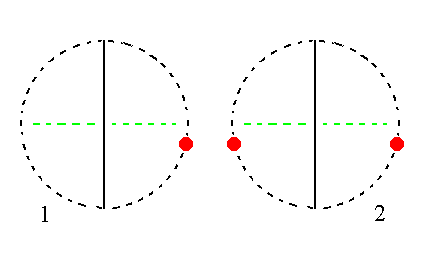  Figure 17.
(1). Position of the face na : b : ~c in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is reflected in the mirror plane resulting in a Monoclinic Hemiprism.
The face a : nb : ~c is also vertical. It generates a monoclinic orthohemiprism when subjected to the symmetry elements of the present Class :   The face is duplicated by the mirror plane resulting in a vertical face pair making up a hemiprism. See Figure 18.

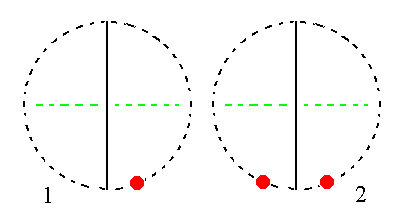  Figure 18.
(1). Position of the face a : nb : ~c in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is reflected in the mirror plane resulting in a Monoclinic Hemiprism.
The face ~a : b : mc is parallel to the clino axis. It generates a monoclinic clinohemidome when subjected to the symmetry elements of the present Class :   The face is duplicated by the mirror plane resulting in a face pair parallel to the clino axis making up a hemidome.
See Figure 19.

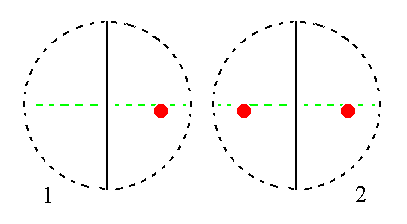  Figure 19.
(1). Position of the face ~a : b : mc in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is reflected in the mirror plane resulting in a Monoclinic Hemidome.
The face a : ~b : mc is parallel to the ortho axis. It generates a monoclinic orthotetartodome when subjected to the symmetry elements of the present Class :   Because the mirror plane is perpendicular to the face it does not generate any new face, so we end up with just our initial face, the tetartodome. See Figure 20.

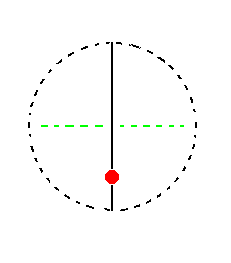  Figure 20.
(1). Position of the face a : ~b : mc in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is not affected by the action of the mirror plane, so the result is a Monoclinic Tetartodome.
The face ~a : b : ~ c is parallel to the clino and vertical axes. It generates a hemihedric monoclinic clinopinacoid when subjected to the symmetry elements of the present Class :   The face is duplicated by the action of the mirror plane resulting in a vertical face pair parallel to the clino axis. See Figure 21.

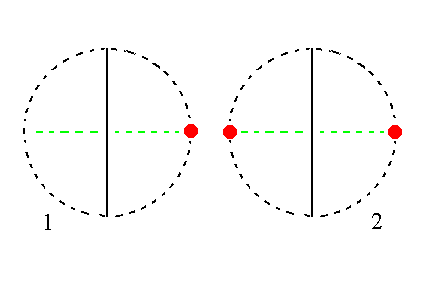  Figure 21.
(1). Position of the face ~a : b : ~ c in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is reflected by the action of the mirror plane resulting in a vertical face pair parallel to the clino axis, a pinacoid.
The face a : ~b : ~c is parallel to the ortho and vertical axes. It generates a monoclinic orthohemipinacoid when subjected to the symmetry elements of the present Class :   Because the mirror plane is perpendicular to the face it does not generate any new face, so we end up with that same initial face, a hemipinacoid. See Figure 22.

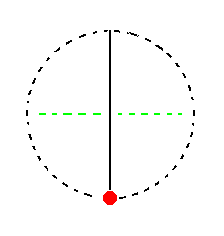  Figure 22.
(1). Position of the face a : ~b : ~c in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is not affected by the action of the mirror plane, so the result is a Monoclinic Hemipinacoid.
The face ~a : ~b : c, finally, is parallel to the clino and ortho axes. It generates a hemihedric monoclinic pedion (= a monoclinic basic hemipinacoid) when subjected to the symmetry elements of the present Class :   Because the mirror plane is perpendicular to the face it generates no new faces, so we end up with that same initial face, a pedion. See Figure 23.

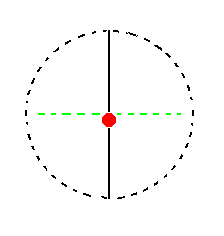  Figure 23.
(1). Position of the face ~a : ~b : c in the stereogram of the symmetry elements of the Monoclinic-domatic Crystal Class.
(2). The face is not affected by the action of the mirror plane, so the result is a Monoclinic Pedion.
This concludes our exposition of the Monoclinic-domatic Crystal Class, and with it our exposition of the Monoclinic Crystal System.
To continue, klick HERE for Part One of the Triclinic Crystal System (Class 1*).

back to homepage

back to Part One

back to Part Two

****************