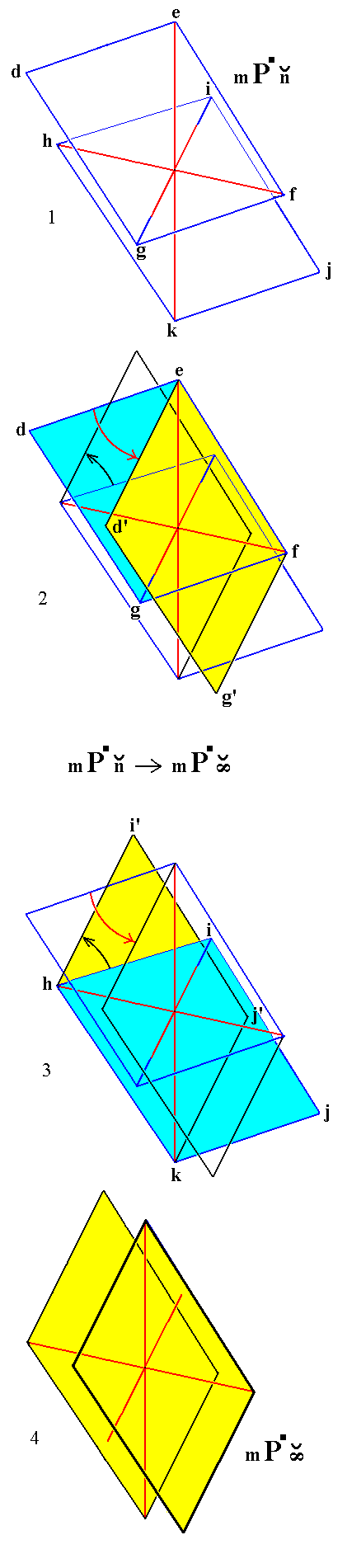The Triclinic Crystal System (Part One)
back to homepage
Introduction
For a general introduction to Crystal Systems and Crystal Classes, see the Essay on The Morphology of Crystals, which the reader should first consult, if he or she is not familiar with Crystal Symmetry and its description.
The reader should also consult the previous Essays on The Tetragonal Crystal System, on The Hexagonal Crystal System, on The Orthorhombic Crystal System and, especially, on The Monoclinic Crystal System in order to fully understand the issues in the present Essay (and the next Essay) on the Triclinic System.
Axial system
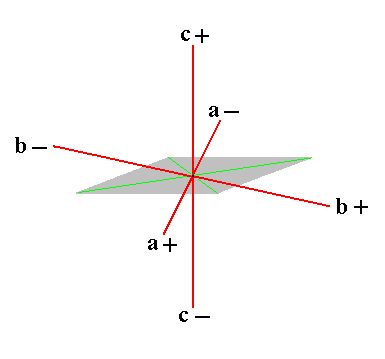
The crystalloghraphic axial system to which the Forms of this Crystal System let themselves refer, consists of three non-equivalent axes, intersecting each other at oblique angles, i.e. angles that are not (necessarily) equal to 900. Of these axes, for (the set-up of) which one chooses appropriate (existing) crystal edges, one sets -- analogously to the Orthorhombic System -- one axis vertically (the c axis, or vertical axis), the longer of the other two -- the macro axis -- transversely, and the other, i.e. the shorter axis -- the brachy axis -- obliquely to the beholder. See Figure 1.
 |
|
Figure 1. The system of crystallographic axes (red lines) for the (description of the) Triclinic Crystal System.
The c+ c- axis is the Vertical Axis.
The b+ b- axis is the Macro Axis.
The a+ a- axis is the Brachy Axis.
These three axes are not perpendicular to each other : an oblique angle obtains between every two of them.
|
The angle obtaining between the vertical axis and the macro axis is denoted by the greek letter alpha.
The angle obtaining between the vertical axis and the brachy axis is denoted by the greek letter beta.
The angle obtaining between the brachy axis and the macro axis is denoted by the greek letter gamma.
Forms and Basic Faces
Recall that a (simple) Form of (i.e. belonging to) a (certain) Crystal Class is a (minimal) set or configuration of crystal faces such that that configuration has a symmetry (content) consistent with that of the relevant Crystal Class.
These Forms (belonging to the same Crystal Class) can enter in combinations with each other in real crystals, then making up (closed) complex Forms.
Also in our present Crystal System many (simple) Forms are possible. We will derive all the different types of these Forms from a set of four Basic Forms.
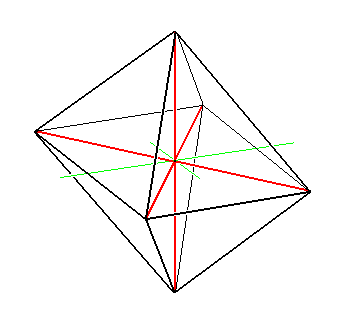
As the one Basic (but complex) Form of the Triclinic Crystal System one can take the Triclinic Bipyramid, consisting of eight faces (four upper and four lower). See Figure 2.
 |
|
Figure 2. The primary Triclinic Bipyramid.
It is a complex Form, that is a combination of four simple Forms each consisting of two parallel faces.
|
Because such a pyramid is already a combination of four simple Forms, namely four triclinic tetartopyramids, each consisting of two parallel faces, we can also take one of these simple Forms -- preferably the one with no minus signs, namely (a : b : c) consisting of the unit face and its parallel counter face -- as the Basic Form of the Triclinic System, from which (a set of) all other Form types can be derived (From the other three Forms making up the triclinic bipyramid, the corresponding sets of all these Form types can be derived).
The next Figure shows how the triclinic bipyramid is made up of four simple Forms, i.e. the four tetartopyramids :
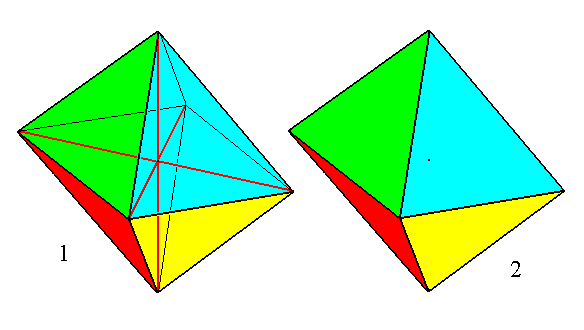
Figure 3.
(1). The primary Triclinic Bipyramid. Each colored face represents a simple Form (consisting of that face and its parallel counter face).
(2). Crystallographic axes and all the edges at the back side of the pyramid removed from the drawing.
All the Forms of the System's highest symmetrical Class (the Holohedric Division of our System) consist of just two parallel faces. This is so because the only symmetry element of (the crystals of) that Class is a center of symmetry : If we imagine a Form of this Class to have more than two faces, then, first of all, it should possess an even number of them, like 4, 6, 8, etc., in order to be consistent with having a center of symmetry. However, such an increase in the number of equivalent faces will introduce extra symmetry elements, like mirror planes or rotation axes. Indeed, in the derivation of triclinic holohedric Forms, following the Facial Approach, we'll see that all the resulting Forms consist of only two faces which are parallel to each other. Such Forms are (also) called pinacoids.
In the next Figure we once again depict the triclinic bipyramid indicating the faces that represent the four tetartopyramids with their corresponding Naumann symbols.
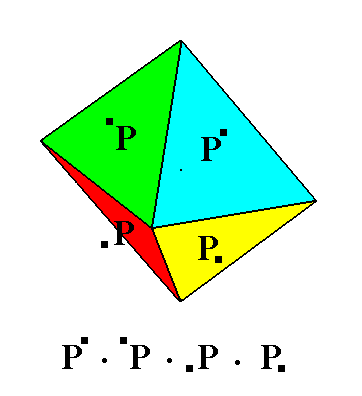 |
|
Figure 4. The primary Triclinic Bipyramid.
It is a complex Form, that is a combination of four simple Forms each consisting of two parallel faces. The (simple) Forms (tetartopyramids) are denoted by their Naumann symbols. The position of the little black squares indicates the position of the face (representing the Form) on the Triclinic Bipyramid.
The symbol for the combination of the four Forms making up the bipyramid is given below the drawing of that pyramid.
|
The Triclinic-pinacoidal Class
(= Holohedric Division of the Triclinic System) 1*
The symmetry elements of this Class are the folowing :
This Crystal Class shows three main types of Forms :
- Forms, the faces of which intersect all three crystallographic axes. We call them pyramids.
- Forms, the faces of which intersect only two crystallographic axes, the prisms and domes (each of which has its faces parallel to a third of these axes).
- Forms, the faces of which intersect only one crystallographic axis, the pinacoids (proper) (each of which has its faces parallel to the two other axes).
1. Pyramids
The unit face (for the Triclinic System) a : b : c intersects all three crystallographic axes at unit distances.
If we consider this face together with its parallel counter face -a : -b : -c, then we have a face configuration that has a symmetry consistent with that of our Class, namely just a center of symmetry. So then we have a (simple) Form. Of course it is an open Form and can only exist when it enters into a combination with other Forms such that a closed face configuration is the result.
Our Form, consisting of the parallel face pair a : b : c and -a : -b : -c, can be denoted by the Naumann symbol 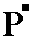 , expressing the fact that its front face can be considered as the upper right front face of the above mentioned triclinic bipyramid (See Figures 2, 3 and 4), which in turn can be considered as a combination of four such Forms -- tetartopyramids.
, expressing the fact that its front face can be considered as the upper right front face of the above mentioned triclinic bipyramid (See Figures 2, 3 and 4), which in turn can be considered as a combination of four such Forms -- tetartopyramids.
The Weissian symbol for this Form is (a : b : c), and the Miller symbol is {111}.
A second Form (belonging to the combination that makes up the triclinic bipyramid) can be conceived when we consider the face a : -b : c together with its parallel counter face
-a : b : -c. Its Naumann symbol can be written as 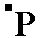 expressing the fact that its front face is the upper left front face of the triclinic bipyramid. Its Weissian symbol is (a : -b : c) and its Miller symbol is {11*1} (where the sign " * " stands for a minus sign placed above the preceding numeral -- as is done in the literature).
expressing the fact that its front face is the upper left front face of the triclinic bipyramid. Its Weissian symbol is (a : -b : c) and its Miller symbol is {11*1} (where the sign " * " stands for a minus sign placed above the preceding numeral -- as is done in the literature).
A third Form (belonging to the combination that makes up the triclinic bipyramid) can be conceived when we consider the face a : -b : -c together with its parallel counter face
-a : b : c. Its Naumann symbol can be written as 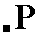 expressing the fact that its front face is the lower left front face of the triclinic bipyramid. Its Weissian symbol is (a : -b : -c) and its Miller symbol is {11*1*}.
expressing the fact that its front face is the lower left front face of the triclinic bipyramid. Its Weissian symbol is (a : -b : -c) and its Miller symbol is {11*1*}.
A fourth Form (belonging to the combination that makes up the triclinic bipyramid) can be conceived when we consider the face a : b : -c together with its parallel counter face
-a : -b : c. Its Naumann symbol can be written as 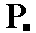 expressing the fact that its front face is the lower right front face of the triclinic bipyramid. Its Weissian symbol is (a : b : -c) and its Miller symbol is {111*}.
expressing the fact that its front face is the lower right front face of the triclinic bipyramid. Its Weissian symbol is (a : b : -c) and its Miller symbol is {111*}.
The Forms we have just discussed are, however, primary Forms, meaning here that in all of them the derivation coefficient m (which refers to the vertical axis) is equal to 1.
In compiling a list of holohedric Forms we will, wherever possible, strive for a listing of just all the Form types, which boils down to enumerating generalized Forms in all cases where such a generalization is possible. The above four Forms will not enter in our list because they are not generalized, but they nevertheless serve as Forms from which all other Forms of the Class can be derived. So let's start to generalize (which is equivalent to the finding of types ) and begin our listing, a listing of the Form types, as well as a listing of all the single faces, the basic faces, representing those Forms.
When we let m vary, then we can discriminate three Series of (derived) tetartopyramids :
- The Vertical Series.
The faces of its Forms intersect the brachy and macro axes at the unit distances associated with them.
These Forms are called Prototetartopyramids.
Such a pyramid can be denoted by the Weissian symbol (a : b : mc), by the Naumann symbol 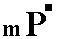 , and by the Miller symbol {hhl}.
, and by the Miller symbol {hhl}.
Like the above case of the primary tetartopyramids, there are three more such Forms together making up the four (derived, i.e. non-primary) prototetartopyramids :
- (a : b : mc),
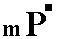
- (a : -b : mc),
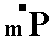
- (a : -b : -mc),
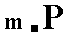
- (a : b : -mc),
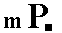
The first of the above four Forms will enter as the first item of our list of Form types, and the face representing it, as the first item of our list of basic faces.
See Figure 5.
- The Brachydiagonal Series.
For the faces of its Forms the derivation coefficient m, as well as n if the latter refers to the brachy axis, can vary such that n is greater than 1.
These Forms are called Brachytetartopyramids.
In the same way as for the above mentioned pyramids there are four such pyramids :
- (na : b : mc),
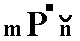
- (na : -b : mc),
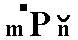
- (na : -b : -mc),
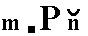
- (na : b : -mc),
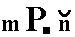
The fact that n refers to the brachy axis is indicated in the Naumann symbol by placing the sign 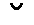 above n.
The first of the above four Forms will enter as the second item of our list of Form types, and the face representing it, as the second item of our list of basic faces.
above n.
The first of the above four Forms will enter as the second item of our list of Form types, and the face representing it, as the second item of our list of basic faces.
See Figure 6.
- The Macrodiagonal Series.
For the faces of its Forms the derivation coefficient m, as well as n if the latter refers to the macro axis, can vary such that n is greater than 1.
These Forms are called Macrotetartopyramids.
In the same way as for the above mentioned pyramids there are four such pyramids :
- (a : nb : mc),
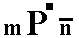
- (a : -nb : mc),
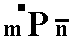
- (a : -nb : -mc),
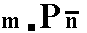
- (a : nb : -mc),
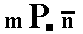
The fact that n refers to the macro axis is indicated in the Naumann symbol by placing the sign 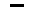 above n.
The first of the above four Forms will enter as the third item of our list of Form types, and the face representing it, as the third item of our list of basic faces.
above n.
The first of the above four Forms will enter as the third item of our list of Form types, and the face representing it, as the third item of our list of basic faces.
See Figure 7.
So with these three Series we now have also found the first three of the basic faces compatible with the Triclinic Crystal System. The basic faces of the Triclinic System are such that from them can be derived the non-primary holohedric Forms by subjecting each of them to the symmetry elements of the most symmetric Class of our Crystal System (See Facial Approach, below).
To summarize, the three already found basic faces are :
a : b : mc
na : b : mc
a : nb : mc
In due course we'll find more of such basic faces.
In the next Figures we have depicted respectively the derivation of a (non-primary) prototetartopyramid (Figure 5), a (non-primary) brachytetartopyramid (Figure 6), and a (non-primary) macrotetartopyramid (Figure 7 and 7a) :
 |
|
Figure 5.
Derivation of a non-primary Prototetartopyramid.
(1). The primary Triclinic Bipyramid, a combination of four (simple) Forms.
(2). Emphasis of the Form
(a : b : c) by extending its two faces (Extension of its faces does not change the Form crystallographically).
(3). Removal of the other Forms.
The Form emphasized and isolated is the Triclinic primary Prototetartopyramid.
Crystallographic axes depicted by red lines.
(4). Construction (derivation) of a Triclinic non-primary Prototetartopyramid by making
m > 1
(5). Result of the construction of a Triclinic non-primary Prototetartopyramid, namely (a : b : mc). The Form consists of two parallel faces.
|
Remark : In reporting on the crystallography of a new triclinic mineral or whatever new crystalline substance, or one that has not been recorded in the literature, the convention should be followed that
c < a < b, in which c is the length of the vertical axis, a the length of the brachy axis, and b the length of the macro axis. In that case the Form depicted in (5) of Figure 5 should be rotated such that the shortest axis becomes vertical. In the above case that would be the axis there signified as the brachy axis which now becomes the vertical axis. The longest axis then should become the macro axis.
After having oriented the Form in that way it then is a macrotetartopyramid (instead of a prototetartopyramid).
The next Figure shows the derivation of a triclinic non-primary brachytetartopyramid.
 |
|
Figure 6.
Derivation of a Triclinic
non-primary Brachy-
tetartopyramid,
from a Triclinic
non-primary Prototetartopyramid.
(1). A Triclinic non-primary Prototetartopyramid.
(2). Increasing the distance (measured from the origin of the axial system) of intersection of the brachy axis. The intersection distances with respect to the vertical and macro axes are held constant.
(3). Construction of the faces of the new Form.
(4). Result of the construction (derivation) of a Triclinic non-primary Brachytetartopyramid.
(5). The same as (4). Coloration applied. The three crystallographic axes are given as red lines.
|
The next two Figures show the derivation of a triclinic non-primary macrotetartopyramid.
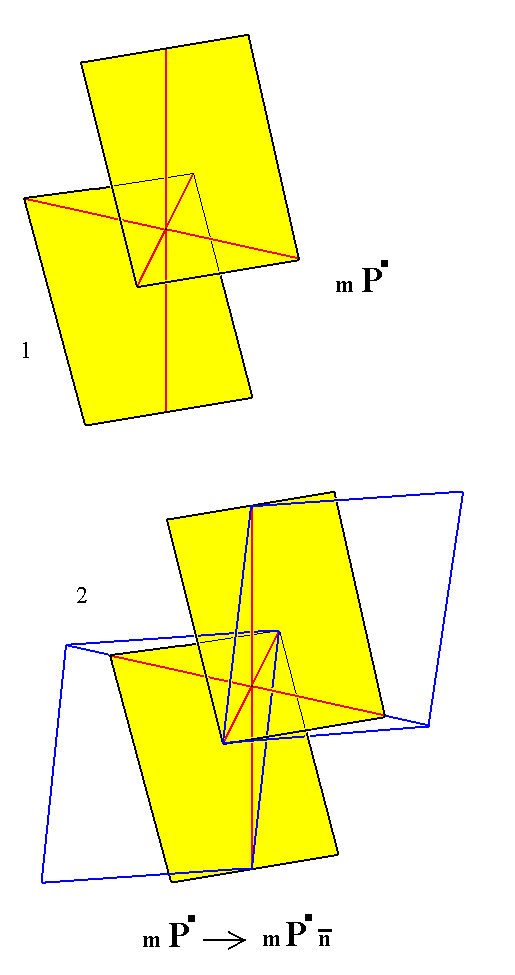
Figure 7.
Derivation of a Triclinic non-primary Macrotetartopyramid from a Triclinic non-primary Prototetartopyramid.
(1). A Triclinic non-primary Prototetartopyramid.
(2). Construction of the Triclinic non-primary Macrotetartopyramid, by increasing the intersection distance with respect to the macro axis. The intersection distances with respect to the brachy and vertical axes are held constant. See further, next Figure.
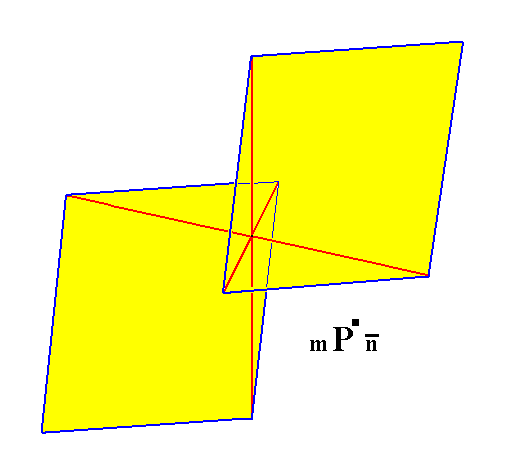
Figure 7a. Result of the construction in Figure 7, a Triclinic non-primary Macrotetartopyramid.
2. Prisms and Domes
These Forms can be derived from the tetartopyramids by letting one derivation coefficient become infinite. This means that their faces intersect two crystallographic axes and are parallel to a third.
The prisms will be derived from the tetartopyramids by letting the derivation coefficient m become infinite resulting in their faces to be parallel to the vertical axis. Because they only consist of two (parallel) faces, they are hemiprisms.
The domes will be derived from the tetartopyramids by letting the derivation coefficient n referring either to the brachy or to the macro axis become infinite, resulting in their faces to be parallel either to the brachy axis or to the macro axis. Because they consist of only two faces they are hemidomes.
2a. Prisms
From the triclinic (tetarto-)pyramids we can derive three types of (hemi-)prism :
- The Protohemiprism, with its Weissian symbol (a : b : ~c), and its Miller symbol {110} (The Naumann symbols are given in the Figures).
- The Brachyhemiprisms, (na : b : ~c).
- The Macrohemiprisms, (a : nb : ~c).
From the triclinic pyramids of the Vertical Series we can derive the triclinic protohemiprism by letting the derivation coefficient m become infinite. Of course it does not matter whether we derive such a hemiprism from a primary (m = 1) or from a non-primary (m unequal to 1) prototetartopyramid. See Figure 8.
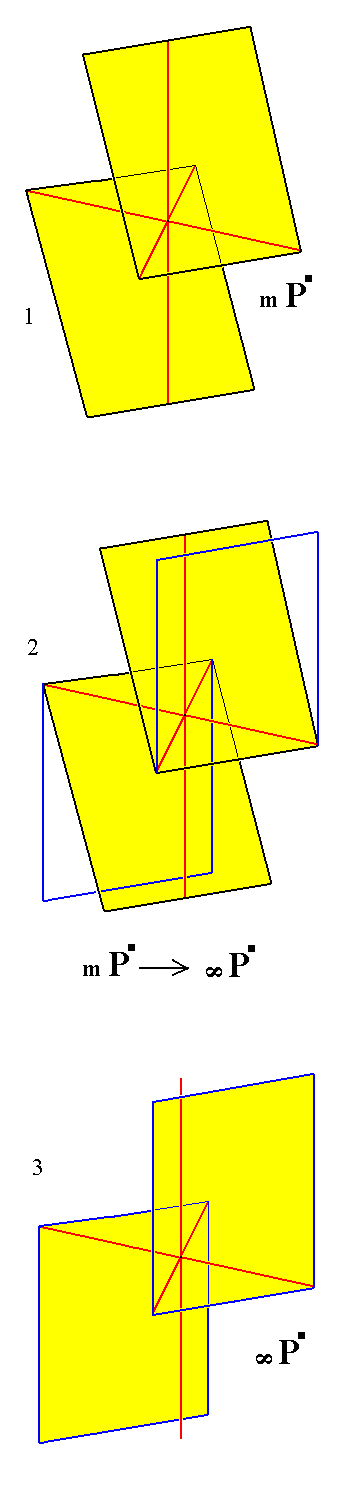 |
|
Figure 8.
Derivation of the Triclinic Protohemiprism.
(1). The (derived) Triclinic Prototetartopyramid.
(2). Construction (derivation) of the Triclinic Protohemiprism from a Triclinic Prototetartopyramid.
(3). Result of the construction. The Form consists of two faces parallel to the vertical axis, and cutting off unit distances from the other two axes.
|
From the pyramids of the Brachydiagonal Series can, in the same way, be derived triclinic brachyhemiprisms, by letting the derivation coefficient m become infinite. See Figure 9.
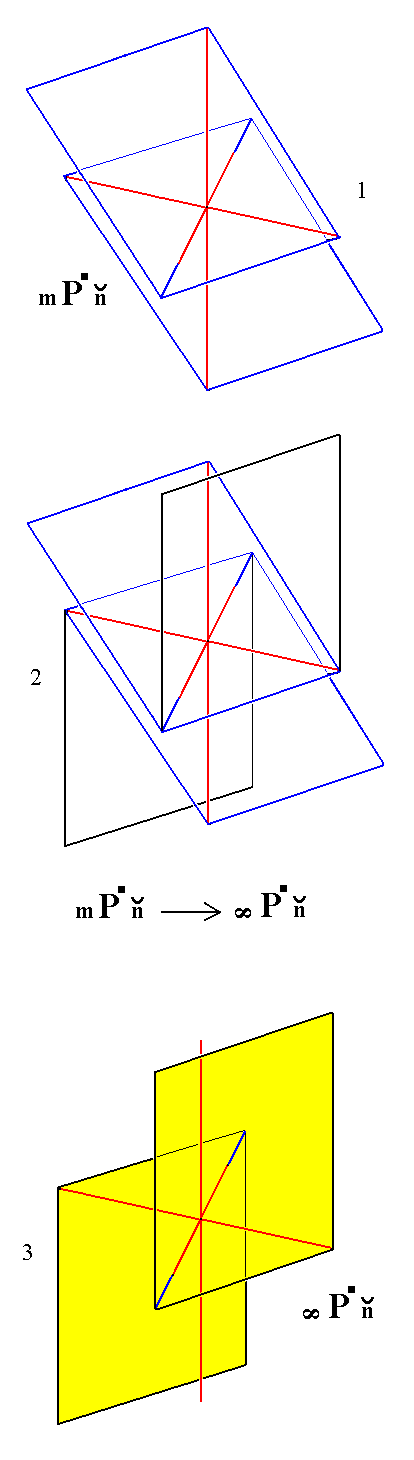 |
|
Figure 9.
Derivation of a Triclinic Brachyhemiprism from a Triclinic Brachytetartopyramid.
(1). A Triclinic (non-primary) Brachytetartopyramid.
(2). Construction (derivation) of a Triclinic Brachyhemiprism from a Triclinic Brachytetartopyramid.
(3). Result of the construction. Again the new Form is a verical face pair.
|
From the pyramids of the Macrodiagonal Series can, in the same way, be derived triclinic macrohemiprisms by letting the derivation coefficient m become infinite. See Figure 10.
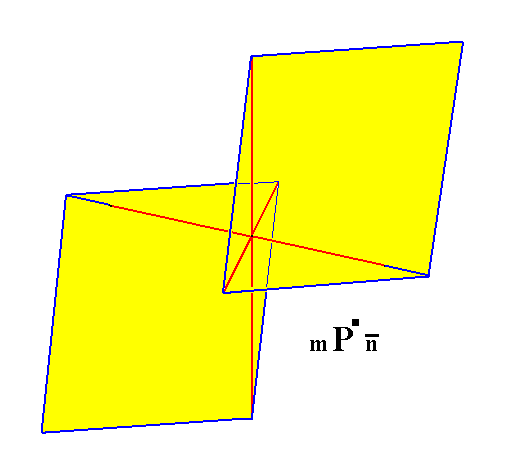
Figure 10. The Triclinic (non-primary) Macrotetartopyramid, from which the Triclinic Macrohemiprism will be derived (Figure 10a and 10b).
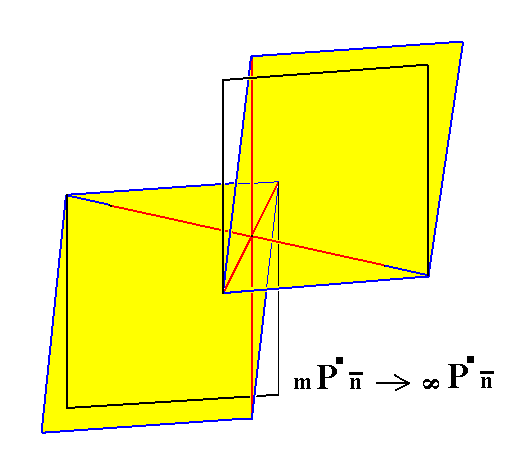
Figure 10a. Construction (derivation) of a Triclinic Macrohemiprism from a Triclinic Macrotetartopyramid.

Figure 10b. Result of the construction of a Triclinic Macrohemiprism.
Above we have derived the triclinic hemiprisms from non-primary triclinic upper right tetartopyramids, i.e. from the Forms :
- (a : b : mc),
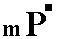
- (na : b : mc),
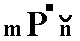
- (a : nb : mc),
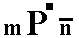
Of course those same hemiprisms can be derived from the respective primary versions of those tetartopyramids.
But still other triclinic hemiprisms can be derived from :
- (a : -b : mc),
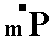
- (na : -b : mc),
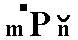
- (a : -nb : mc),
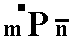
I.e. from the upper left tetartopyramids.
The other tetartopyramids, the lower left and the lower right, do not yield new hemiprisms as is clear from the next Figure (in this case concerning a primary triclinic bipyramid, but that is immaterial for the derivation of hemiprisms).
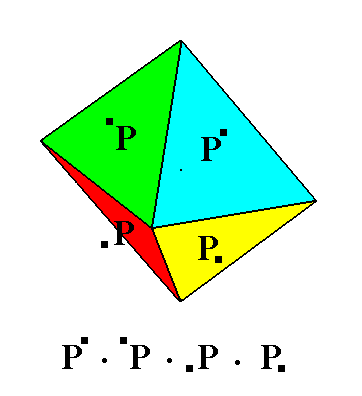 |
|
Figure 11 (= Figure 4). The primary Triclinic Bipyramid.
It is a complex Form, that is a combination of four simple Forms each consisting of two parallel faces. The (simple) Forms (tetartopyramids) are denoted by their Naumann symbols. The position of the little black squares indicates the position of the face (representing the Form) on the Triclinic Bipyramid.
The symbol for the combination of the four Forms making up the bipyramid is given below the drawing of that pyramid.
|
When we let the face, representing the Form 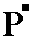 and its parallel counter face (together making up that Form), become vertical we get the right (in contradistinction to left) protohemiprism,
and its parallel counter face (together making up that Form), become vertical we get the right (in contradistinction to left) protohemiprism, 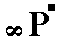 .
.
Exactly this same Form is obtained, however, when we let the face, representing the Form 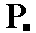 and its parallel counter face, become vertical.
and its parallel counter face, become vertical.
When we let the face, representing the Form 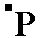 and its parallel counter face, become vertical we get the left protohemiprism,
and its parallel counter face, become vertical we get the left protohemiprism, 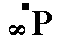 .
.
Exactly the same Form is obtained, however, when we let the face, representing the Form 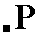 and its parallel counter face, become vertical.
and its parallel counter face, become vertical.
So only two protohemiprisms are possible, a right one and a left one, denoted by the Naumann symbols 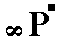 and
and  .
.
The same applies with regard to the brachy- and macrohemiprisms, except that in their case more than one right and more than one left hemiprisms are possible because of the varying of the derivation coefficient n, referring either to the brachy axis or to the macro axis.
With the derivation of the vertical prisms we have found three more basic faces :
a : b : ~c
na : b : ~c
a : nb : ~c
2b. Domes
Domes are in fact tilted prisms. Also here such Forms consist of only two parallel faces, which makes them hemidomes. There are two types of triclinic (hemi-)domes, namely brachyhemidomes, (~a : b : mc), i.e. Forms consisting of two faces parallel to the brachy axis, but cutting the vertical axis either at unit distance (primary hemidomes) or at a rational multiple of it (non-primary, i.e. derived hemidomes). The same goes for the macro axis. Here we can set the face at the macro axis' unit distance and then the value for m (referring to the vertical axis) is determined as some rational multiple of its corresponding unit distance (i.e. the unit distance associated with the vertical axis).
The second type of triclinic (hemi-)dome is represented by the macrohemidomes,
(a : ~b : mc), i.e. Forms also consisting of two faces, but which are parallel to the macro axis. Like the brachyhemidomes they are not parallel to the vertical axis. When they intersect the brachy axis at unit distance then the value for m (referring to the vertical axis) is some rational multiple of its corresponding unit distance (i.e. the unit distance associated with the vertical axis).
Recall that if we have a unit face (chosen for the Crystal System concerned) that cuts off distances (measured from the origin of the axial system) a, b, c from the respective crystallographic axes, and if we also have another face that cuts off the distances p, q, r, then the derivation coefficients of that second face are p/a, q/b and r/c, where a, b and c are set as unit distances. So the derivation coefficient relating to, say, the vertical axis, namely r/c, is equal to the number of times that the unit distance (c), associated with the vertical axis, fits in the vertical axis' cutt-off distance (r) of the second face.
The Miller indices are the reciprocals of the derivation coefficients reduced to whole numbers (The minus sign, where it occurs, is then placed above the relevant index. On this website we then set an asterix after and above that index). The Miller indices -- together constituting the Miller symbol -- characterizing a face are then placed between ordinary brackets. When they characterize a Form they are placed between { }.
2b1. Brachydomes
From a triclinic non-primary brachytetartopyramid can be derived a triclinic non-primary brachyhemidome by letting the derivation coefficient n (referring to the brachy axis) become infinite. See Figure 12.
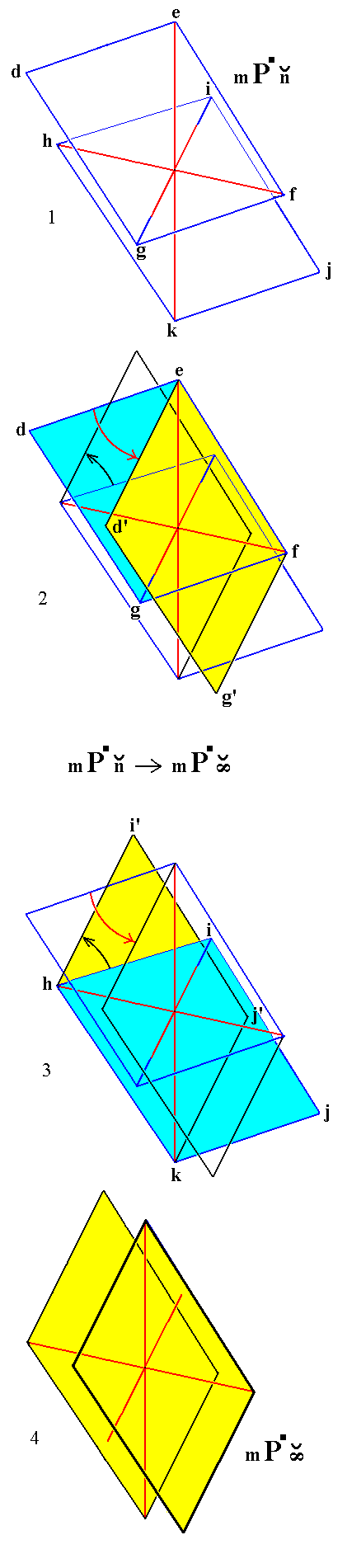 |
|
Figure 12.
Derivation of a Triclinic (non-primary) Brachyhemidome from a Triclinic (non-primary) Brachytetartopyramid.
(1). Two parallel faces defg and hijk making up a Triclinic (non-primary) Brachytetartopyramid. Red lines (including blue extensions) indicate the three crystallographic axes.
(2)and (3). Construction (derivation) of a Triclinic Brachyhemidome from a Triclinic Brachytetartopyramid. The two faces become parallel to the brachy axis.
(2). Both faces of the tetartopyramid are rotated such that they become parallel to the brachy axis. Here (in (2)) the rotation of the face defg is emphasized. It is rotated (red arrow) about the hinge ef till it is parallel to the brachy axis, becoming the face d'efg'. It is now the front face of the Brachyhemidome. In (3) the rotation of the other face of the tetartopyramid is emphasized.
(3). Emphasizing the rotation (black arrow) of the face hijk about the hinge hk till it is parallel to the brachy axis. It has then become the back face, hi'j'k, of the Brachyhemidome.
(4). The result of the construction of a Triclinic Brachyhemidome. It is a Form consisting of two faces parallel to the brachy axis, but intersecting the vertical axis and the macro axis.
|
Above we have constructed the brachyhemidome from a(n upper right) brachytetartopyramid, but of course the same brachyhemidome can be derived from any (upper right) tetartopyramid.
Besides this right brachyhemidome yet another brachyhemidome can be derived, namely from the upper left tetartopyramid. It will be the left brachyhemidome. Two such hemidomes together make up a brachydome, i.e. an inclined prism parallel to the brachy axis. So such a prism is a combination of two (simple) Forms.
The lower right tetartopyramid does not yield a new Form because the rotation of its front face, till it is parallel to the brachy axis results in a face that is identical to the parallel counter face of the (front face of the) left brachyhemidome.
The lower left tetartopyramid also does not yield any new Form because the rotation of its front face till it is parallel to the brachy axis results in a face that is identical to the parallel counter face of the (front face of the) right brachyhemidome.
2b2. Macrodomes
From a triclinic non-primary macrotetartopyramid can be derived a triclinic non-primary macrohemidome, by letting the derivation coefficient n (now referring to the macro axis) become infinite. See Figure 13.
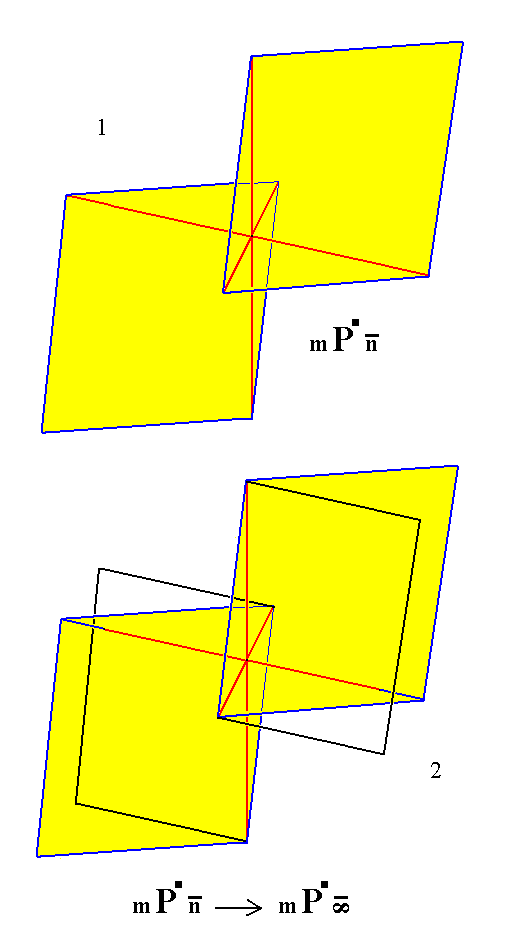
Figure 13.
(1). A Triclinic non-primary Macrotetartopyramid.
(2). Construction (derivation) of a Triclinic non-primary Macrohemidome from the tetartopyramid of (1), by rotating the faces of the tetartopyramid about the respective hinges, one of them formed by the line connecting the intersection point on the positive vertical axis with the intersection point on the positive brachy axis, while the other hinge is formed by the line connecting the intersection point on the negative vertical axis with the intersection point on the negative brachy axis.
The result of this construction is shown in Figure 13a.
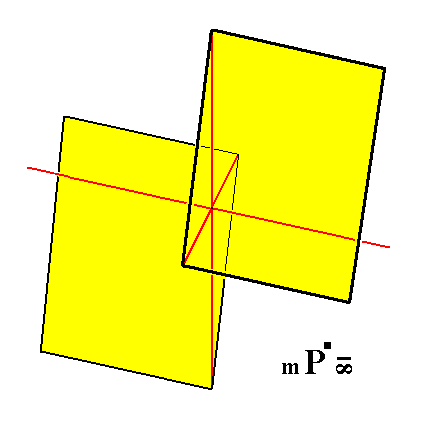
Figure 13a. A Triclinic non-primary Macrohemidome, a Form consisting of two faces parallel to the macro axis but intersecting the brachy as well as the vertical axis.
Above we constructed a macrohemidome by rotating the faces of the tetartopyramid 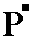 till they were parallel to the macro axis.
till they were parallel to the macro axis.
Exactly the same Form will be obtained by totating the faces of the tetartopyramid 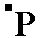 .
.
The lower tetartopyramids 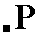 and
and 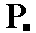 give identical macrohemidomes but different from those derived from the upper pyramids. So we have in fact just upper macrohemidomes (which can vary with respect to the derivation coefficient m, referring to the vertical axis) and lower macrohemidomes. Going together, a lower and an upper macrohemidome will constitute a macrodome, i.e. a combination of two (simple) Forms. Such a macrodome is an inclined prism parallel to the macro axis.
give identical macrohemidomes but different from those derived from the upper pyramids. So we have in fact just upper macrohemidomes (which can vary with respect to the derivation coefficient m, referring to the vertical axis) and lower macrohemidomes. Going together, a lower and an upper macrohemidome will constitute a macrodome, i.e. a combination of two (simple) Forms. Such a macrodome is an inclined prism parallel to the macro axis.
With the domes we have found yet two more basic faces :
~a : b : mc
a : ~b : mc
3. Pinacoids
A triclinic pinacoid is a face pair parallel to two of the three crystallographic axes, while from the other axis the faces cut off a unit distance -- in the positive or negative direction of that axis -- associated with that axis.
There are three (types of) pinacoids (s. str.) depending on which axis is intersected :
- Brachypinacoid, (~a : b : ~c), resp. {010}.
- Macropinacoid, (a : ~b : ~c), resp. {100}.
- Basic Pinacoid, (~a : ~b : c), resp. {001}.
They can be derived from tetartopyramids.
3a. Brachypinacoid
The triclinic brachypinacoid can be derived from a triclinic tetartopyramid by letting its faces become parallel to the brachy and vertical axes. This is most simply done by taking a brachyhemidome, which is itself derived from a tetartopyramid, by letting the derivation coefficient m (referring to the vertical axis) become infinite, as is done in the next Figure.
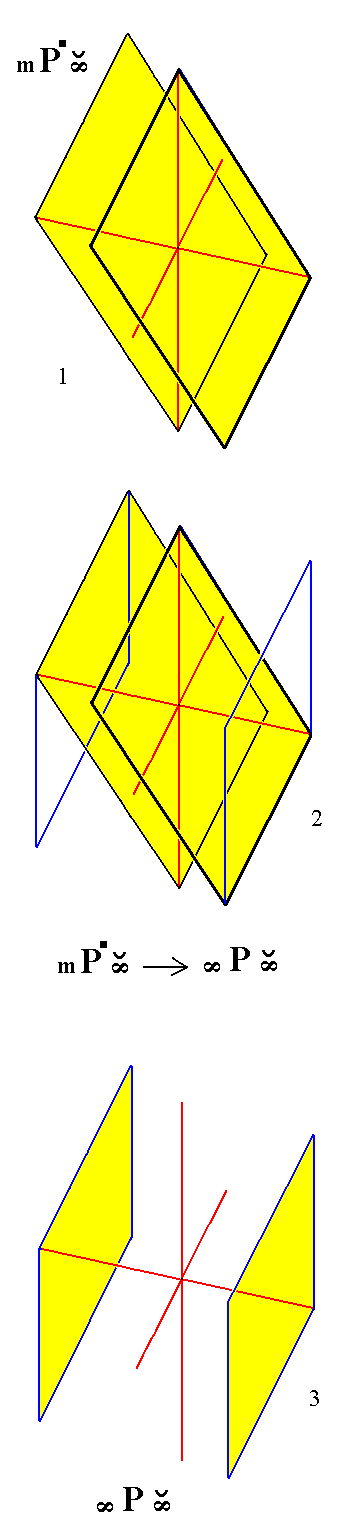 |
|
Figure 14.
Derivation of the Triclinic Brachypinacoid from a Triclinic Brachyhemidome.
(1). A Triclinic non-primary Brachyhemidome.
(2). Construction (derivation) of the Triclinic Brachypinacoid from a Triclinic Brachyhemidome, by letting its faces become vertical.
(3). Result of the construction of the Triclinic Brachypinacoid.
|
3b. Macropinacoid
The triclinic macropinacoid can be derived from a triclinic tetartopyramid by letting its faces become parallel to the macro and vertical axes. This is most simply done by taking a macrohemidome, which is itself derived from a tetartopyramid, by letting the derivation coefficient m (referring to the vertical axis) become infinite, as is done in the next Figure.
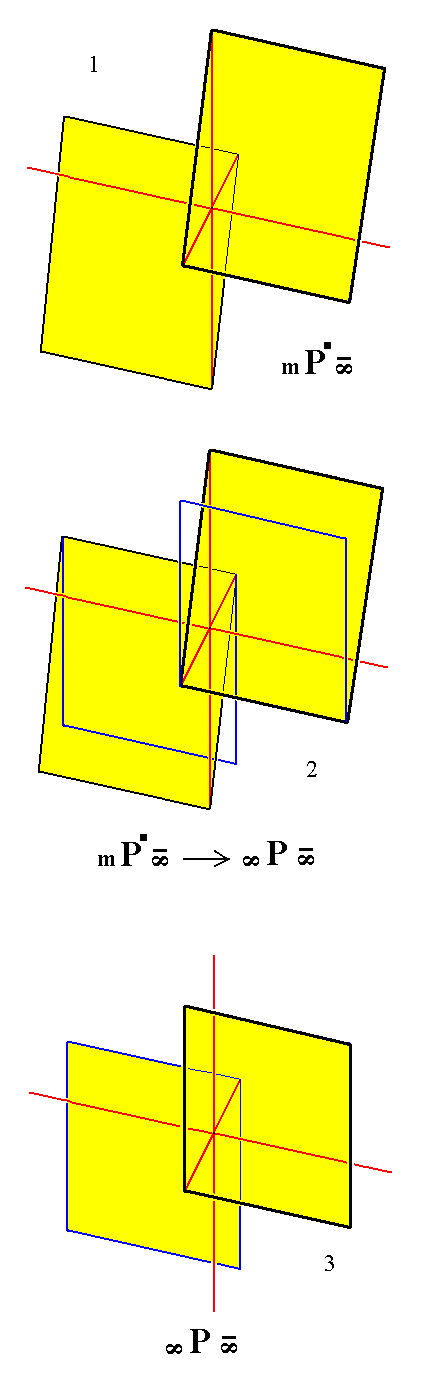 |
|
Figure 15.
Derivation of the Triclinic Macropinacoid from a Triclinic Macrohemidome.
(1). A Triclinic non-primary Macrohemidome.
(2). Construction (derivation) of the Triclinic Macropinacoid from a Triclinic Macrohemidome, by letting its faces become vertical.
(3). Result of the construction of the Triclinic Macropinacoid.
|
3c. Basic Pinacoid
From any triclinic tetartopyramid, (a : b : c), (a : b : mc), (na : b : mc), (a : nb : mc), can be derived the basic pinacoid, by letting the derivation coefficient for a and for b become infinite, which implies that the two faces now are parallel to the plane in which the brachy and macro axes lie, in other words, the faces are parallel to the brachy as well as to the macro axis. Consequently the Weissian symbol for the basic pinacoid is (~a : ~b : c), its Naumann symbol is 0P and its Miller symbol is {001}.
In the next Figure we will derive the basic pinacoid from the primary prototetartopyramid,
(a : b : c).
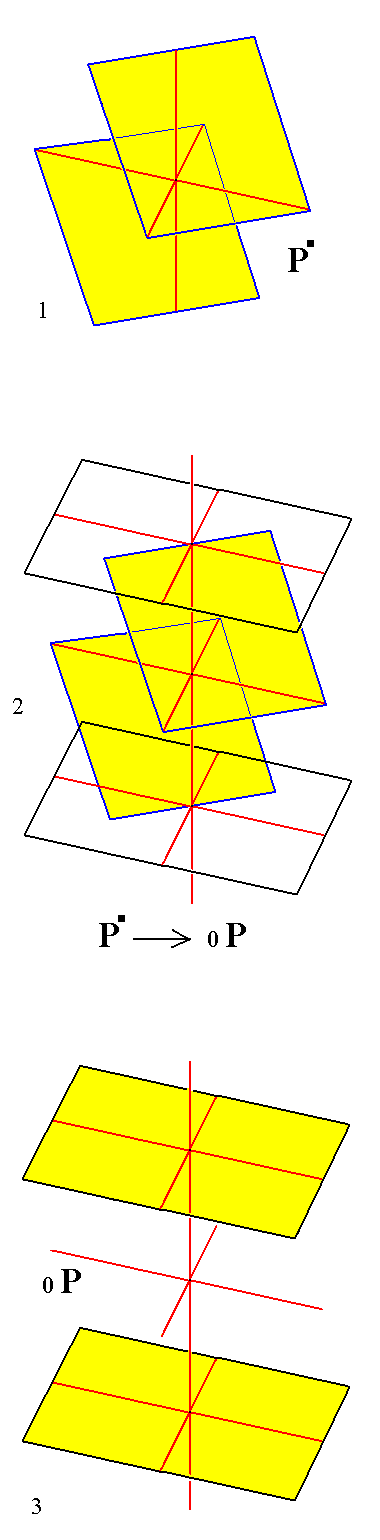 |
|
Figure 16.
Derivation of the Triclinic Basic Pinacoid from a Triclinic Prototetartopyramid.
(1). The Triclinic primary Prototetartopyramid.
(2). Construction (derivation) of the Triclinic Basic Pinacoid from a Triclinic Prototetartopyramid, by letting its faces become parallel to the brachy and macro axes.
(3). Result of the construction of the Triclinic Basic Pinacoid.
|
With the pinacoids we have found the last basic faces :
~a : b : ~c
a : ~b : ~c
~a : ~b : c
This concludes our derivation of all the Forms of the Triclinic-pinacoidal Crystal Class (= Holohedric division of the Triclinic System).
All these Forms can, and in this case must, enter into combinations with each other in real crystals such that closed (complex) Forms appear.
So a triclinic crystal belonging to the present Class -- the System's most symmetric Class -- consists of a set of parallel face pairs, together making up a complex, closed Form. See the next Figure.
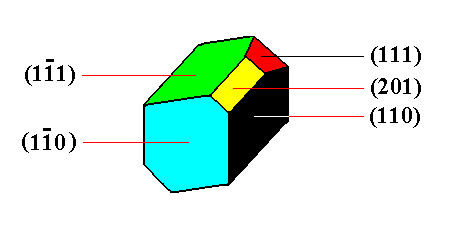
Figure 17. A sketch of a holohedric triclinic crystal (of the mineral Axinite). Its faces are marked with Miller symbols.
In the above Figure we see a combination of five Forms. Each face, visible in the Figure, has a parallel counter face and as such, i.e. as parallel face pair, makes up a Form.
(110) is the front face of the right protohemiprism (a : b : ~c).
(11*0) is the front face of the left protohemiprism (which is independent
of the right hemiprism) (a : -b : ~c).
(111) is the front face of the primary upper right prototetartopyramid (a : b : c).
(11*1) is the front face of the primary upper left prototetartopyramid (a : -b : c).
(201) is the front face of a non-primary upper macrohemidome (a : ~b : 2c).
With all these Forms we now also have a complete list of basic faces that we can use to again derive the Forms of the present Class as well as those of the next Class. The list reads :
a : b : mc
na : b : mc
a : nb : mc
a : b : ~c
na : b : ~c
a : nb : ~c
~a : b : mc
a : ~b : mc
~a : b : ~c
a : ~b : ~c
~a : ~b : c
FACIAL APPROACH
We will now derive those same Forms by subjecting the above listed basic faces one by one to the symmetry elements of the present Class. These symmetry elements are :
Recall that a face configuration having a center of symmetry with respect to a certain point, means that the configuration is left unchanged when subjected to a reflection in that point (also called an inversion), not to be confused with a reflection in a plane.
The next Figure illustrates a face configuration, consisting of the faces A and A', having a center of symmetry (cs).
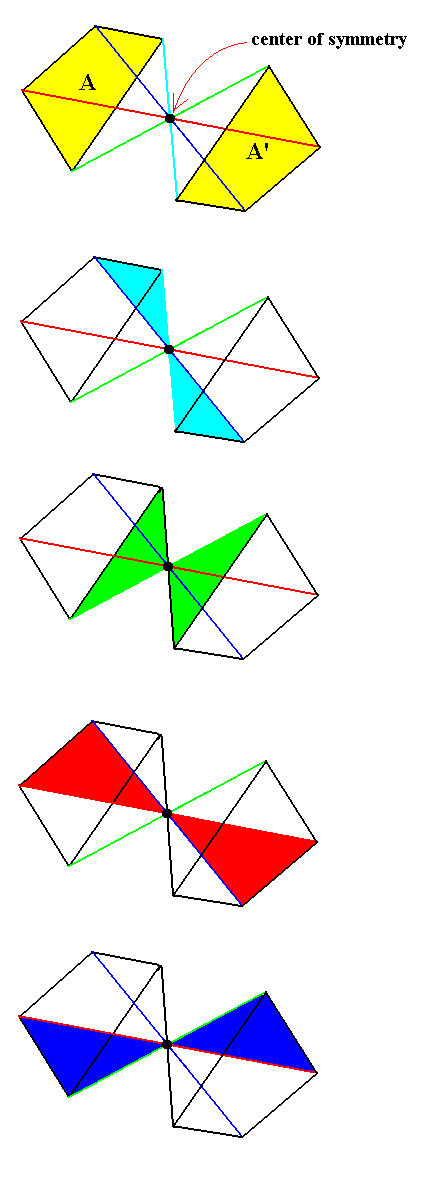
Figure 18. The symmetry of a face configuration, consisting of the faces A and A', consistent with a center of symmetry (cs).
The derivations of the Forms will be done with the help of stereographic projections.
The next Figure is a stereographic projection of (1) the symmetry elements of the present Class, (2) the projections of all the face poles of a most general Form, a Triclinic non-primary Brachytetartopyramid, (na : b : mc), and (3) the projections of the piercing points of the brachy and macro axes (i.e. the projection onto the projection plane of the intersection points of the axes with the projection sphere).
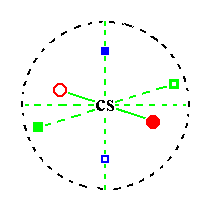
Figure 19. Stereographic projection of the symmetry elements (this Class having just a center of symmetry, cs ) of the Triclinic-pinacoidal Crystal Class, and of the face poles (red dot and red circle) of a most general Form.
Blue squares are projections of the piercing points of the brachy axis (open square : projection coming from below, solid square : projection coming from above the projection plane).
Green squares are projections of the peircing points of the macro axis (The projection of the piercing points of the c axis (vertical axis) is located in the center of the projection plane (not indicated in the Figure)).
The above Figure is meant to be a very general one, i.e. us not having a specific triclinic crystal in mind. We can see that the brachy axis is not perpendicular to the vertical axis because the projections of its piercing points fall within the projection plane, i.e. not on its perimeter. The same is the case with the macro axis. Moreover we can see that the macro axis is not perpendicular to the brachy axis. The angles alpha, beta and gamma between the crystallographic axes vary, their values depend on the crystallized substance under investigation.
Before we are going to derive all the Forms with the aid of the stereographic projection we'll first ponder a little more about the stereographic projection features of triclinic crystals.
Stereographic projection of triclinic crystals
In Figure 19a we show -- approximately -- the position of all the basic faces listed above. Each of such a face is the front face of a simple Form, so we name those faces by the Forms they represent.
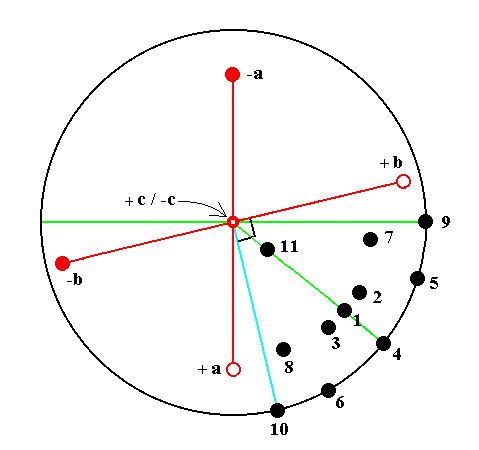
Figure 19a. Position of the eleven Basic Faces (listed above), representing the eleven simple Forms (Form types) :
- Triclinic Prototetartopyramid.
- Triclinic Brachytetartopyramid.
- Triclinic Macrotetartopyramid.
- Triclinic Protohemiprism.
- Triclinic Brachyhemiprism.
- Triclinic Macrohemiprism.
- Triclinic Brachyhemidome.
- Triclinic Macrohemidome.
- Triclinic Brachypinacoid.
- Triclinic Macropinacoid.
- Triclinic Basic Pinacoid.
The symmetry elements are not indicated in this Figure (the only symmetry element present in crystals of this Class -- the Triclinic-pinacoidal Class -- is a center of symmetry), so one should not interpret the solid perimeter of the projection plane, drawn in this Figure, as being a horizontal mirror plane.
The brachy axis is indicated by +a -------- -a
The macro axis is indicated by +b -------- -b
7 represents a Brachyhemidome. At first one would expect it to lie on the line
[+c/-c --- 9] , but because the brachy axis is inclined the face pole will come to lay somewhat beneath that line.
Something similar goes for the Macrohemidome. At first one would expect it to lie on the line [+c/-c --- 10] perpendicular to the trace of the macro axis, but because the macro axis is inclined the face pole representing the Macrohemidome will come to lie somewhat to the right of that line.
The faces 11, 7 and 9 lie on the same zone parallel to the brachy axis (A zone is a set of all crystal faces, belonging to some crystal, parallel to a certain direction, say a crystallographic axis.). 11 is the basic pinacoid, it is parallel to the brachy axis but also to the macro axis.
A second zone is formed by the faces 11, 8 and 10. This zone is parallel to the macro axis. The basic pinacoid not only belongs to the first zone mentioned, but also to this zone because it is parallel to the macro axis.
The face a : b : mc generates a triclinic prototetartopyramid when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry resulting in a parallel face pair, the prototetartopyramid. See Figure 20.
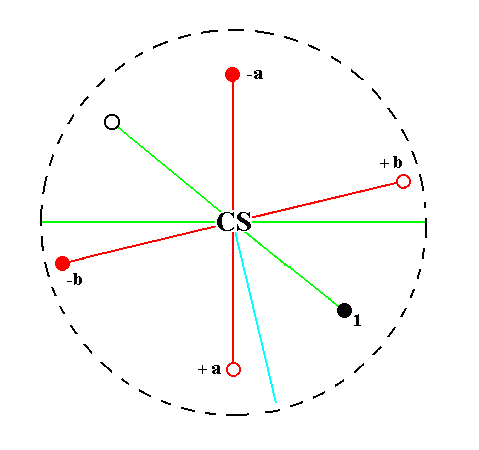
Figure 20.
Position of the face a : b : mc (black opaque dot) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (small black open circle).
The face na : b : mc generates a triclinic brachytetartopyramid when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is a brachytetartopyramid. See Figure 21.
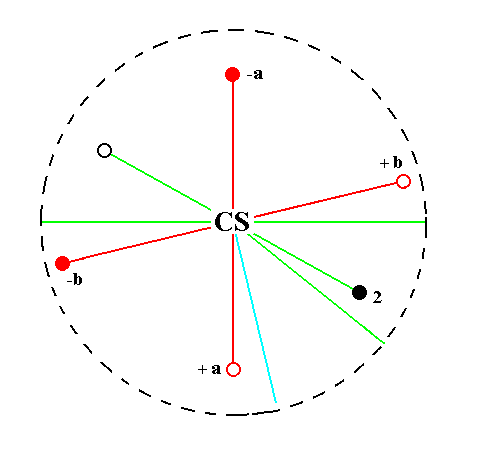
Figure 21.
Position of the face na : b : mc (black opaque dot) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (small black open circle).
The face a : nb : mc generates a triclinic macrotetartopyramid when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is a macrotetartopyramid. See Figure 22.
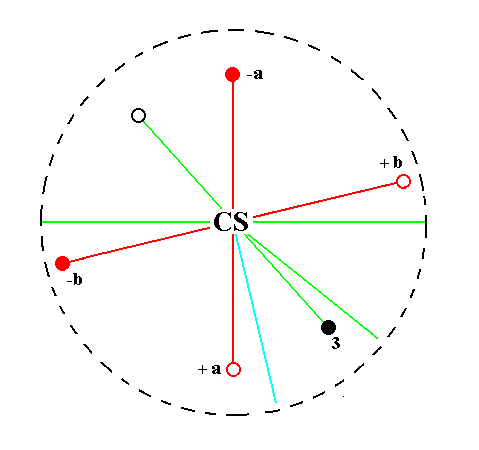
Figure 22.
Position of the face a : nb : mc (black opaque dot) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (small black open circle).
The face a : b : ~c is vertical. It generates the triclinic protohemiprism when it is subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is a protohemiprism.
See Figure 23.
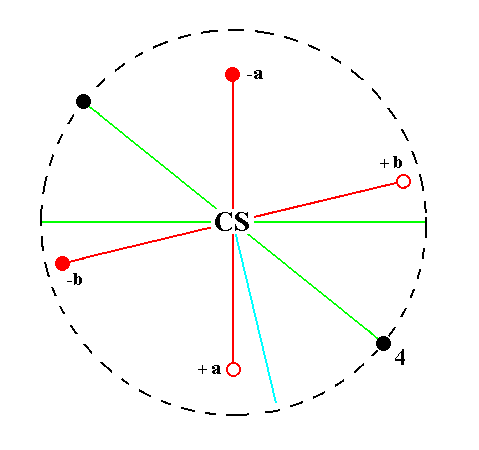
Figure 23.
Position of the face a : b : ~c (black opaque dot in the lower right quadrant of the stereogram) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (black opaque dot in the upper left quadrant of the stereogram).
The face na : b : ~c is also vertical. It generates a triclinic brachyhemiprism when subjected to the symmetry elements of the present Class :
The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is a brachyhemiprism. See Figure 24.
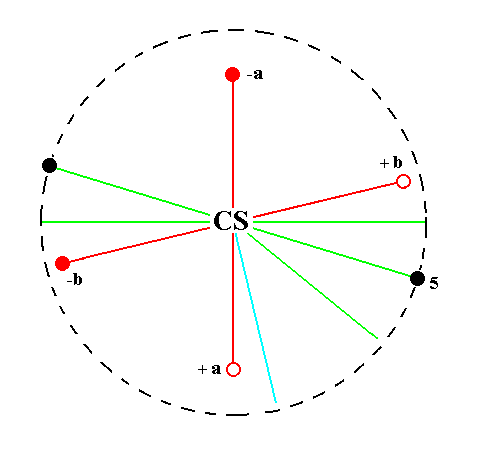
Figure 24.
Position of the face na : b : ~c (black opaque dot in the lower right quadrant of the stereogram) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (black opaque dot in the upper left quadrant of the stereogram).
The face a : nb : ~c is also vertical. It generates a triclinic macrohemiprism when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is a macrohemiprism. See Figure 25.
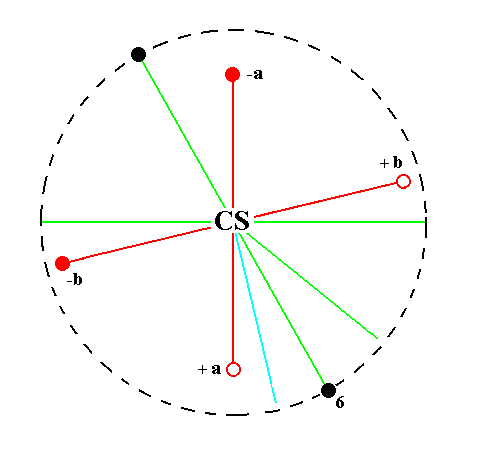
Figure 25.
Position of the face a : nb : ~c (black opaque dot in the lower right quadrant of the stereogram) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (black opaque dot in the upper left quadrant of the stereogram).
The face ~a : b : mc generates a triclinic brachyhemidome when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is a brachyhemidome.
See Figure 26.
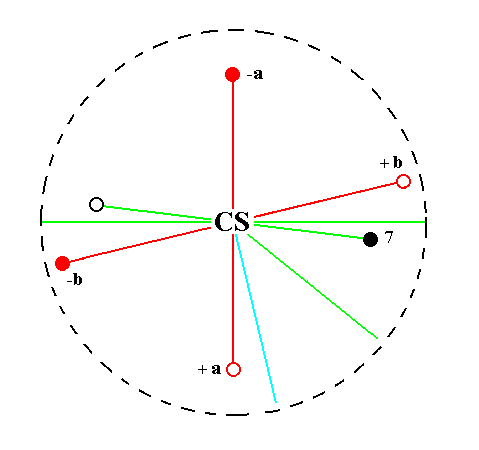
Figure 26.
Position of the face ~a : b : mc (black opaque dot in the lower right quadrant of the stereogram) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (small black open circle in the upper left quadrant of the stereogram).
The face a : ~b : mc generates a triclinic macrohemidome when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is a macrohemidome.
See Figure 27.
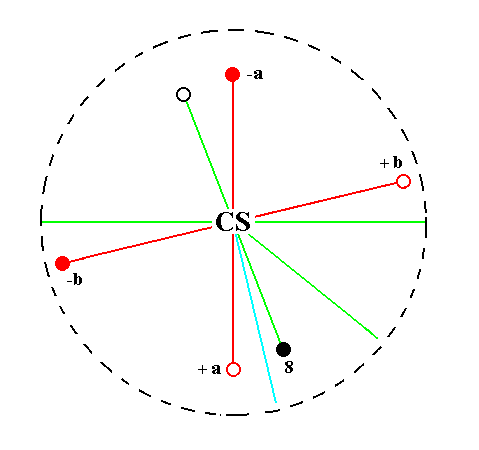
Figure 27.
Position of the face a : ~b : mc (black opaque dot in the lower right quadrant of the stereogram) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (small black open circle in the upper left quadrant of the stereogram).
The face ~a : b : ~c is vertical. It generates the triclinic brachypinacoid when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is vertical and parallel to the brachy axis, it is a brachypinacoid. See Figure 28.
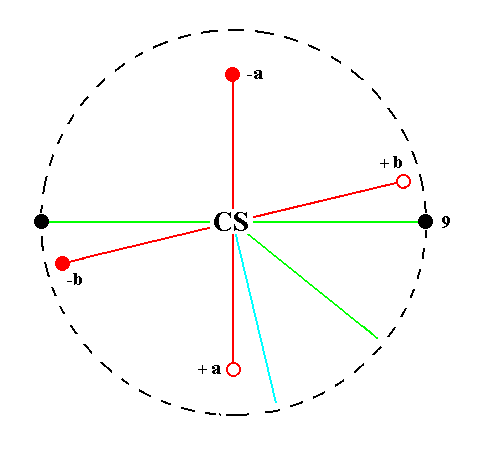
Figure 28.
Position of the face ~a : b : ~c (black opaque dot at the right side of the stereogram) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (black opaque dot at the left side of the stereogram).
The face a : ~b : ~c is also vertical. It generates the triclinic macropinacoid when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is vertical and parallel to the macro axis, it is a macropinacoid. See Figure 29.
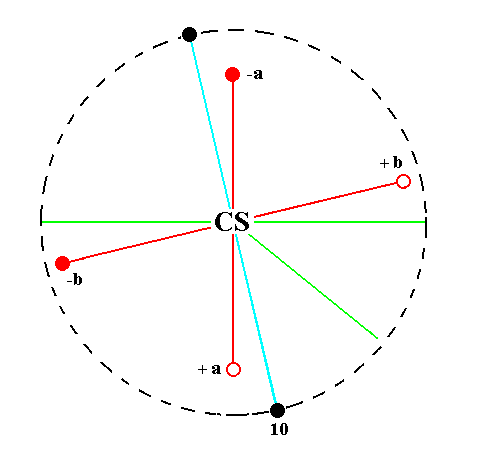
Figure 29.
Position of the face a : ~b : ~c (black opaque dot in the lower right quadrant of the stereogram) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (black opaque dot in the upper left quadrant of the stereogram).
The face ~a : ~b : c, finally, is parallel to the brachy and macro axes. It generates a triclinic basic pinacoid when subjected to the symmetry elements of the present Class : The face is reflected in the center of symmetry yielding a second face parallel to the initial one. The resulting face pair is parallel to the brachy and macro axis, it is a basic pinacoid. See Figure 30.
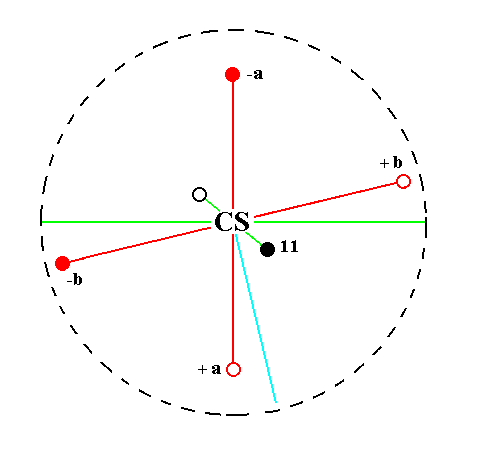
Figure 30.
Position of the face ~a : ~b : c (black opaque dot in the lower right quadrant of the stereogram) in the stereogram of the symmetry elements of the Triclinic-pinacoidal Crystal Class.
The center of symmetry generates a parallel counter face (small black open circle in the upper left quadrant of the stereogram).
This concludes our exposition of the Triclinic-pinacoidal Crystal Class.
To continue, klick HERE for Part Two (Class 1).
back to homepage
****************



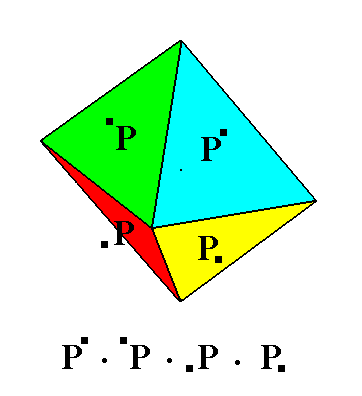
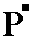 , expressing the fact that its front face can be considered as the upper right front face of the above mentioned triclinic bipyramid (See Figures 2, 3 and 4), which in turn can be considered as a combination of four such Forms -- tetartopyramids.
, expressing the fact that its front face can be considered as the upper right front face of the above mentioned triclinic bipyramid (See Figures 2, 3 and 4), which in turn can be considered as a combination of four such Forms -- tetartopyramids.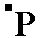 expressing the fact that its front face is the upper left front face of the triclinic bipyramid. Its Weissian symbol is (a : -b : c) and its Miller symbol is {11*1} (where the sign " * " stands for a minus sign placed above the preceding numeral -- as is done in the literature).
expressing the fact that its front face is the upper left front face of the triclinic bipyramid. Its Weissian symbol is (a : -b : c) and its Miller symbol is {11*1} (where the sign " * " stands for a minus sign placed above the preceding numeral -- as is done in the literature).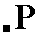 expressing the fact that its front face is the lower left front face of the triclinic bipyramid. Its Weissian symbol is (a : -b : -c) and its Miller symbol is {11*1*}.
expressing the fact that its front face is the lower left front face of the triclinic bipyramid. Its Weissian symbol is (a : -b : -c) and its Miller symbol is {11*1*}. 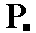 expressing the fact that its front face is the lower right front face of the triclinic bipyramid. Its Weissian symbol is (a : b : -c) and its Miller symbol is {111*}.
expressing the fact that its front face is the lower right front face of the triclinic bipyramid. Its Weissian symbol is (a : b : -c) and its Miller symbol is {111*}. 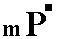 , and by the Miller symbol {hhl}.
, and by the Miller symbol {hhl}. 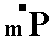
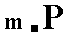
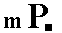
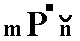
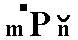
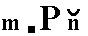
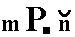
 above n.
The first of the above four Forms will enter as the second item of our list of Form types, and the face representing it, as the second item of our list of basic faces.
above n.
The first of the above four Forms will enter as the second item of our list of Form types, and the face representing it, as the second item of our list of basic faces. 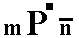
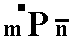
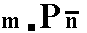
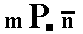
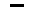 above n.
The first of the above four Forms will enter as the third item of our list of Form types, and the face representing it, as the third item of our list of basic faces.
above n.
The first of the above four Forms will enter as the third item of our list of Form types, and the face representing it, as the third item of our list of basic faces. 








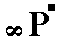 .
. 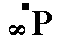 .
.