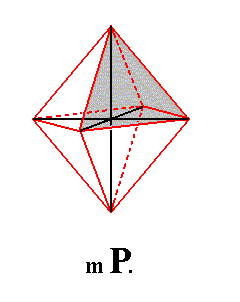
(Alternative name : Quadratic System)
The Tetragonal Crystal System differs from the Isometric System in the fact that one of its three axes of its axial system stands out, and can be interpreted as the main axis. This means that crystals (grown in a homogeneous environment) either are flattened or elongated.
Conventionally one places this main axis vertical. The two other axes, secondary axes, are perpendicular to the main axis, and are equal in length, and perpendicular to each other. The main axis is either shorter or longer than the secondary axes (even when, in some crystals, it happened to have the same actual length, it still is not equivalent to either secondary axis.
Also in this System we recognize a unit face and a basic Form, from which we can derive all other Forms. Here, like in all the remaining Crystal Systems, we encounter, besides closed Forms, also open Forms, i.e. Forms that do not completely enclose a volume of space. Open Forms cannot exist as real crystals, they can only occur in combinations that do enclose space.
Recall that each Form is generated from a face, by the requirement that the generated Form should have the complete symmetry content of the relevant Crystal Class. Forms of the same Crystal Class can combine, increasing the number of faces. Recall also that for faces only their orientation with respect to the above described system of crystallographic axes counts. So their description only contains their orientatation (inclination). Parallel faces, in the sense that the second face originates by a (parallel) shift of the first face, are crystallographically equivalent.
Also here we'll start with the highest symmetrical Class of the System, the Holohedric Division, derive its Forms and describe some combinations. Then we'll derive the lower symmetric Classes by means of merohedric operations, i.e. applying the concepts of hemihedric, tetartohedric, etc., and again by means of subjecting each basic face (compatible with the Crystal System under consideration) to the symmetry operations of the relevant Class.
| Division | Class | mirror planes |
axes | cs |
| Holohedric | Ditetragonal-bipyramidal 4/m 2/m 2/m |
1 + (2 + 2) | one [4] two + two [2] |
+ |
| Hemimorphy of Holohedric |
Ditetragonal-pyramidal 4 m m |
2 + 2 | one [4] p. | - |
| Pyramidal Hemihedric |
Tetragonal-bipyramidal 4/m |
1 | one [4] | + |
| Hemimorphy of Pyramidal Hemihedric |
Tetragonal-pyramidal 4 |
- | one [4] p. | - |
| Trapezohedric Hemihedric |
Tetragonal-trapezohedric 4 2 2 |
- | one [4] two + two [2] |
- |
| Sphenoidic Hemihedric |
Tetragonal-scalenohedric 4* 2 m |
2 | one + two [2] | - |
| Sphenoidic Tetartohedric |
Tetragonal-bisphenoidic 4* |
- | one [4*] | - |
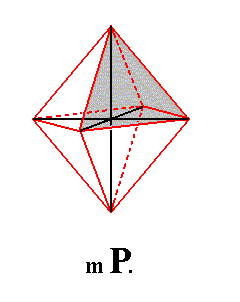
Figure 1. Tetragonal system of crystallographic axes, and a derived Protopyramid as a possible Form of the Class. One face of this Form is emphasized by a grey shade.
The symmetry content (bundle) of the Ditetragonal-bipyramidal Crystal Class is :
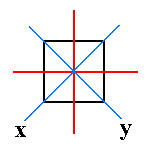
Figure 2. The equatorial plane of the tetragonal protopyramid, and the traces of the 2 + 2 vertical mirror planes. One set of them (blue) contains, besides the vertical, the horizontal crystallographic axes, the other set makes an angle of 450 with the first set, and only contains the vertical crystallographic axis.
The Holohedric Division of the Tetragonal Crystal System has seven primary Forms :
There are seven basic types of faces, and when we subject each face to the symmetry of our present Crystal Class (which means that we demand that the Forms generated from the faces have the symmetry of the Class) we generate the above Forms. The faces are :
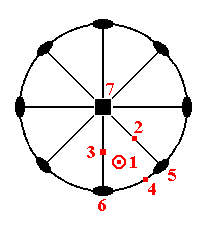
Figure 2a. Stereographic projection of the symmetry elements of the Ditetragonal-bipyramidal Crystal Class (= Holohedric Division), and of the seven basic faces compatible with the Tetragonal Crystal System. The indicated faces are multiplied by the symmetry elements and accordingly show up in the stereograms. But in the present figure only one representation of each face is shown.
In the stereogram of Figure 2a. we see a (vertical) 4-fold rotation axis, represented by a black square. This axis, as represented in the Figure, is perpendicular to the screen (or paper). Perpendicular to this axis is the equatorial mirror plane, represented by a solid circle in the plane of the screen (paper). It coincides with the circumference of the projection plane. Further we see (the traces of) two sets of vertical mirror planes. One set of which contains, besides the main axis, the secondary crystallographic axes, i.e. one member of this set contains one secondary axis, the other member contains the other. The second set of vertical mirror planes bisects the angles obtaining between the planes of the first set. All these vertical mirror planes are represented by straight solid lines. Finally we see two sets of 2-fold rotation axes. One set coinciding with the secondary crystallogaphic axes, the other set bisects the angles between the members of the first set. They are represented by small solid ellipses. So all the symmetry elements of the Class are represented in the stereogram.
The seven basic faces, compatible with the Tetragonal Crystal System are also represented in the Figure. As has been said, the numbers correspond to those of the above list of basic faces :
The primary protopyramid, primary bipyramid of type I, is derived from the upper right front face (the unit face of the Tetragonal Crystal System) -- a : a : c, number 2 of Figure 2a -- of the image in Figure 3 (below) -- considered as just being present on its own, without other faces, and which is in fact a certain conspicuous face on some tetragonal crystal chosen to serve as a unit face. The primary protopyramid is derived from this face by demanding that the generated Form possesses the complete symmetry bundle of the present Class : The face is multiplied by the 4-fold rotation axis resulting in a total of four faces. Then this quadruplet will be doubled by the horizontal mirror plane resulting in the protopyramid.
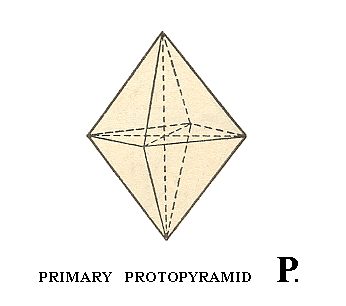
Figure 3. The primary Tetragonal Protopyramid ( = Tetragonal Bipyramid of type I).
Each face of this Form cuts off a finite piece of each crystallographic axis, and, considering it as the basic Form we can denote it by the Weiss symbol (a : a : c), in which the two a's express the equivalence of the two horizontal crystallographic axes, and the one c expresses the fact that the vertical crystallographic axis is not equivalent to either horizontal one.
The protopyramid is a bipyramid bounded by eight isosceles triangles. Its equatorial plane has the shape of a square. The Naumann symbol is P, and the Miller symbol is {111} (the derivation coefficients of the Weiss symbol and the indices of the Miller symbol are set equal to 1, because all other Forms are considered to be derivations of this one Form).
The stereographic projection of the (faces, i.e. all the faces, of the) tetragonal protopyramid is depicted in Figure 3a.
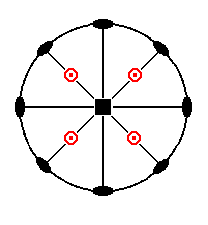
Figure 3a. Stereogram of the Tetragonal Protopyramid. An upper face (pole) is represented by a red dot. A lower face (pole) is represented by a small circle. In the present case their positions on the projection plane coincide. So we see four sets of two faces each, an upper and a lower one.
The first derived Forms are bipyramids like the protopyramid but with a different a : c ratio when compared with the primary protopyramid of Figure 3. The general Weiss symbol for such pyramids is consequently (a : a : mc), the Naumann symbol is mP (the letter before P relates to the cut-off piece of the vertical crystallographic axis), the Miller symbol is {hhl}.
In figure 1 we already saw such a derived protopyramid (assuming m having there some rational value), and in the figure below we see two examples of derived protopyramids with m = 2 and m = 1/2 respectively (If we would set up a stereogram of such a derived protopyramid we would get the same picture as Figure 3a, but with the projections of the faces closer to the perifery of the projection plane or closer to the center of it respectively.
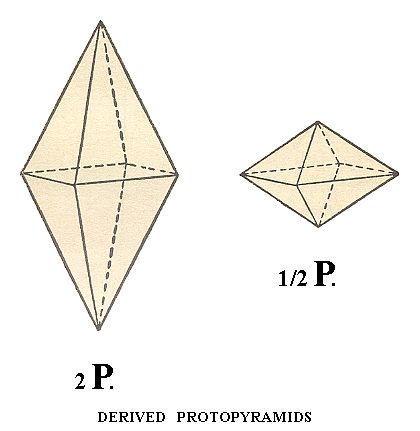
Figure 4. Derived Tetragonal Protopyramids, with m = 2 (left) and m = 1/2 (right).
In the next Figure we see two more Forms, namely (1) the deuteropyramid and the ditetragonal pyramid.
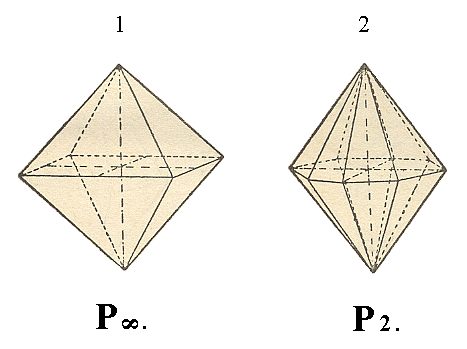
Figure 5. 1. primary Deuteropyramid ( = Tetragonal Bipyramid of type II) , 2. Ditetragonal bipyramid.
While a protopyramid is generated by subjecting the face a : a : mc to all the symmetry operations of the present Crystal Class (when m = 1 we get the primary protopyramid), a deuteropyramid is generated by subjecting the face a : ~a : mc to all those symmetry operations (when m = 1 -- 3 in Figure 2a -- we get the primary deuteropyramid).
The shape of the deuteropyramid (tetragonal bipyramid of type II) does not differ from that of the protopyramid. It differs in its orientation with respect to the crystallographic axes. Each of its faces cuts off pieces only from the main axis and from one of the secondary (i.e. horizontal) axes, and is parallel to the other secondary axis.
So the Weiss symbol is (a : ~a : c), or generally, because also derived pyramids are possible, (a : ~a : mc), and the Naumann symbol is mP~ (the sign before P relates to the main axis, the sign after P to the secondary axis)(Recall that the sign ~ stands for infinity, in Figures denoted by a horizontal 8). The Miller symbol is {h0l}.
The stereographic projection of the deuteropyramid is depicted in Figure 5a.
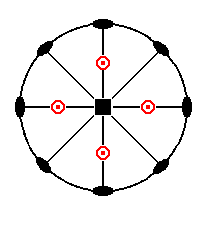
Figure 5a. Stereogram of the Tetragonal Deuteropyramid.
When we subject the face a : na : mc, i.e. a face of which the orientation with respect to the crystallographic axes is the most general, to all the symmetries of the present Crystal Class, we obtain a ditetragonal bipyramid, as yet another Form of the Holohedric Division. The ditetragonal bipyramid has 16 faces, which are oriented such that each of them intersects all three axes at different distances. The equatorial plane is a ditetragon, i.e. an octagon ( = figure with eight sides) having all sides of equal length but with alternating equal angles (See Figure 6.)
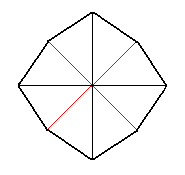
Figure 6. A Ditetragon, the equatorial plane of the Ditetragonal bipyramid.
The general Weiss symbol is (a : na : mc) (1 in Figure 2a), the Naumann symbol is mPn, and the Miller symbol is {hkl}. Limiting Forms are the protopyramid, when n = 1, and the deuteropyramid, when n = ~.
The stereographic projection of the ditetragonal bipyramid is depicted in Figure 5b.
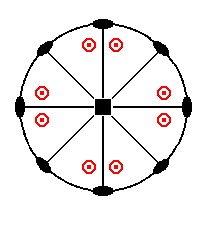
Figure 5b. Stereogram of the Ditetragonal Bipyramid.
When for the described pyramids the derivation coefficient m increases the pyramids become more and more sharp. When the coefficient finally is equal to infinity the sides of the pyramids have become vertical (i.e. parallel to the main crystallographic axis) and the Forms become prisms. These are open Forms which, in their conventional oriention do not enclose space completely. Their top and bottom are open.
From the (primary) protopyramid we derive the protoprism ( = tetragonal prism of type I), by letting the unit face, the one which is situated in front, up, and to the right, become steeper and steeper until it is vertically oriented, implying that the cut-off piece (intercept) of the vertical axis is infinite (in length), while the cut-offs of the other two axes remain the same. This new face can be denoted by a : a : ~c (5 of Figure 2a). When we subject this face to all the symmetries of our Crystal Class we will obtain a protoprism as a new Form.
Its Weiss symbol is (a : a : ~c), the Naumann symbol is ~P., and the Miller symbol is {110}.
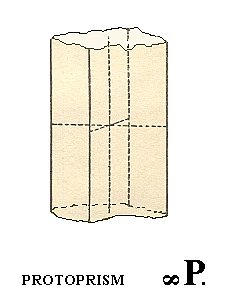
Figure 7. A Protoprism, derived from a (face of the) Protopyramid. An open Form.
Because the protoprism (and also all other prisms) is an OPEN Form, the next Figure does not correctly depict it, by reason of its suggesting the presence of top and bottom faces (while the protoprism lacks these faces). In fact the Figure depicts a combination of protoprism and basic pinacoid (A basic pinacoid is an open Form, consisting of two horizontal parallel faces. See below).
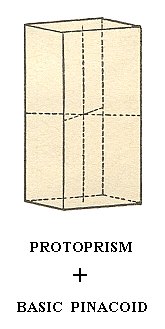
Figure 8. A combination of a Protoprism and a Basic Pinacoid, forming the top and bottom faces of the (combined) Form.
The stereographic projection of the protoprism is depicted in Figure 7a.
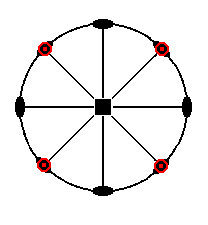
Figure 7a. Stereogram of the Tetragonal Protoprism.
The projection of each face is indicated in the figure as if they represented the coincidence of an upper and lower face pole. But in fact each prism face leads to only one face pole. I depict them nevertheless as is done in the figure in order that the symbols for the 2-fold rotation axes are not obscured by the (projections of the) poles.
A next Form is the deuteroprism ( = tetragonal prism of type II). It derives from the deuteropyramid in the same way that the protoprism was derived from (a face of) the protopyramid, and is distinguished from the protoprism only by its orientation with respect to the crystallographic axes. So the deuteroprism is generated from the face a : ~a : ~c (6 of Figure 2a).
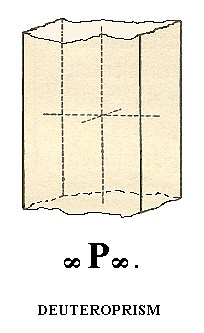
Figure 9. Deuteroprism, an open Form of the Holohedric Division.
The following Figure gives this same deuteroprism, but now closed by a basic pinacoid :
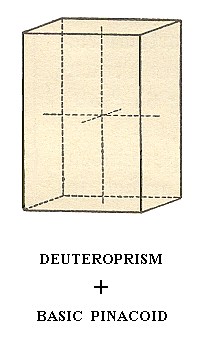
Figure 10. A Deuteroprism, closed by a basic (i.e. horizontal) Pinacoid.
The Weiss symbol for the deuteroprism is (a : ~a : ~c), the Naumann symbol is ~P~., and the Miller symbol is {100}.
The stereographic projection of the deuteroprism is depicted in Figure 9a.
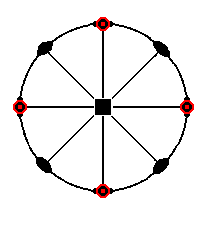
Figure 9a. Stereographic projection of the Tetragonal Deuteroprism.
See the remark at Figure 7a concerning the representation of the projection of the face poles.
The next Form is the ditetragonal prism. It can be derived from the ditetragonal bipyramid (See Figure 5 (2), by isolating a face and letting it become vertical. We then have the face a : na : ~c (4 of Figure 2a). When we subject this face to all the symmetries of our Crystall Class we'll get the ditetragonal prism : The isolated face will be doubled by the nearby mirror plane resulting in two symmetrically related faces having an angle between each other smaller than 1800. This pair of faces will then be multiplied four times by the action of the 4-fold rotation axis, resulting in the ditetragonal prism, consisting of eight vertical faces. Its horizontal outline (i.e. when seen from above, or below) is the same as that of the equatorial plane of the corresponding ditetragonal bipyamid (See also Figure 6).
The Weiss symbol is (a : na : ~c), its Naumann symbol is ~Pn., and the Miller symbol is {hk0}.
See Figure 11. Here we depict the ditetragonal prism as if it is closed by a basic pinacoid (top and bottom faces) for reasons of clarity.
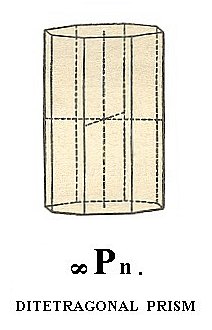
Figure 11. The Ditetragonal Prism.
The stereographic projection of the ditetragonal prism is depicted in Figure 11a.
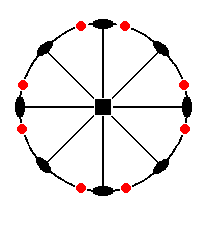
Figure 11a. Stereogram of the Ditetragonal Prism.
Finally we have the basic pinacoid. We already spoke about it earlier. Like the prisms it is an open Form. It consists of two horizontal parallel faces (because the faces are horizontal it is called a basic pinacoid. In other Crystal Classes there also exist pinacoids which are not oriented horizontally). A pinacoid can also be called parallelohedron. See figure 12.
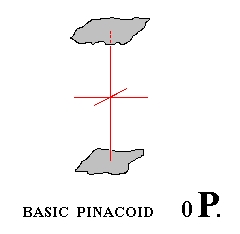
Figure 12. A Basic Pinacoid (Basic Parallelohedron), another open Form of the Holohedric Division.
The basic pinacoid will be generated when we take a horizontally oriented face -- such a face can be denoted by ~a : ~a : c (7 of Figure 2a) -- and subject it to the symmetry of the present Class. The 4-fold rotation axis and the vertical mirror planes will have no effect, but the horizontal mirror plane will duplicate the face (the 2-fold rotation axes will have the same effect), so we'll end up with a Form consisting of two parallel horizontal faces, the basic pinacoid, which is, as has been said, an open Form and can only occur in certain combinations, for example with a prism.
The Weiss symbol is (~a : ~a : c), the Naumann symbol is 0P., and the Miller symbol is {001}.
The "0" in the Naumann symbol 0P means that the face is inclined by an amount of zero, i.e. it is horizontal. We can think of it as the upper right front face of the protopyramid, with its steepness decreased all the way down to zero, i.e. its coefficient for c has become zero. But of course the coefficient can have whatever value, including 1, because varying its hight above or below the origin of the system of crystallographic axes does not change the crystallographic character of the face (a parallel shift of a face does not change its crystallographic character, but notice that parallel faces are not necessarily crystallographically equivalent. The two faces of a pinacoid are equivalent, they involve the same atomic aspect to the environment, and so implying the same physical behavior. In fact all the faces constituting a Form are equivalent in this respect. As we will see further below there exist (in other Classes than the present one) Forms consisting of just one face. Such a Form is called a pedion. And it is possible that, together with other Forms, two pedions combine, forming a pair of parallel faces. But these faces are not equivalent because they belong to different forms, a pedion and another pedion).
The stereographic projection of the basic pinacoid is depicted in Figure 12a.
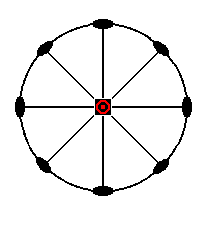
Figure 12a. Stereogram of the Basic Pinacoid.
All these Forms can engage in combinations with each other. In the Figures 13 and 14 we show some examples.
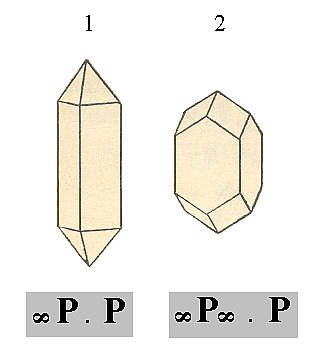
Figure 13. 1. Protoprism + Protopyramid. 2. Deuteroprism + Protopyramid.
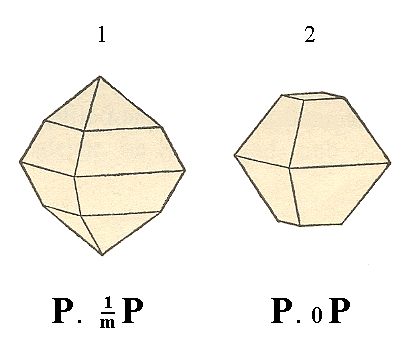
Figure 14. 1. Protopyramid + derived Protopyramid. 2. Protopyramid + Basic Pinacoid (The polar corners of the pyramid are cut off by the Basic Pinacoid).
As real representatives of the Ditetragonal-bipyramidal Class we could mention :
 Rutile - the Alps, twin, about 10mm.
Rutile - the Alps, twin, about 10mm.
This concludes our exposition of the Ditetragonal-bipyramidal Crystal Class.
THE FORMS OF THE LOWER SYMMETRICAL CLASSES.
To continue, klick HERE for Part Two.