back to Part One(Alternative name : Quadratic System)
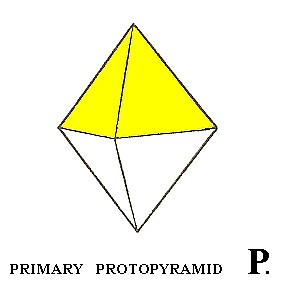
Let us start with the first holohedric Form, the protopyramid. From the next Figure it is evident that we can derive two four-sided (mono)pyramids, one from the colored faces and one from the white faces :
Figure 15. Applying hemimorphy to the Protopyramid yields two type I monopyramids.
In Figure 16 and 17 we depict the two resulting monopyramids.
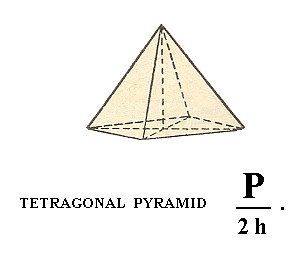
Figure 16. The Tetragonal Pyramid of type I, derived from the colored faces of the protopyramid (= bipyramid of type I) of Figure 15.
In the Naumann symbol I have added a h in order to distinguish this hemihedric (namely hemimorphy) from other hemihedrics.
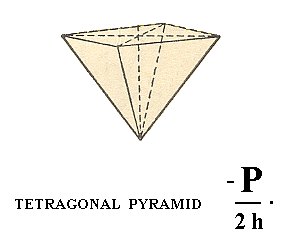
Figure 17. Tetragonal pyramid of type I, derived from the white faces of the protopyramid ( = bipyramid of type I) of Figure 15.
When these two Forms combine, the bipyramid is restored, but crystallographically the horizontal mirror plane is still absent, which will be evident by physical differences.
In fact the figures 16 and 17 each depict a combination of (1) a monopyramid and (2) a face which is called a pedion (this is a single face, that results after subjecting a pinacoid to hemimorphy. See below). The pedion closes the pyramid. But although this pedion is in fact drawn in each Figure, we interpret these Figures, and also all other like figures, as single open Forms, unless otherwise stated. I draw these closing faces (instead of the broken-off faces of, say, Figure 7) for reasons of clarity with respect to interpreting the image.
When we apply hemimorphy to the deuteropyramid ( = bipyramid of type II) (Figure 5, 1) we again obtain two type II monopyramids, one of which is depicted in Figure 18.
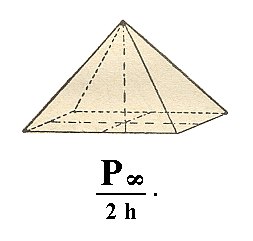
Figure 18. Tetragonal Pyramid of II type, derived from the Deuteropyramid ( = bipyramid of type II)).
The From the ditetragonal bipyramid (Figure 5, 2) we can derive two hemimorphous ditetragonal monopyramids, one of which is depicted in Figure 19.
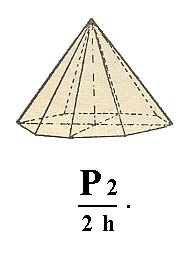
Figure 19. A Ditetragonal Monopyramid, derived from a holohedric Ditetragonal Bipyramid by applying a hemimorphy.
As can be seen in Figure 20, the protoprism ( = tetragonal prism of type I) will not change its outer shape when it is subjected to hemimorphy. So the resulting Form is (still) a tetragonal prism of type I, but it has nonetheless lost its horizontal plane of symmetry.
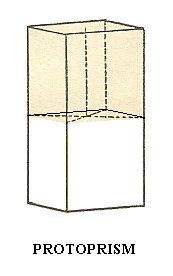
Figure 20. A Protoprism does not change its outer shape when subjected to hemimorphy, but despite its outer appearance it does not possess a main mirror plane anymore which can become evident by physical features.
Precisely the same is the case for the other prisms :
The deuteroprism ( = tetragonal prism of type II) yields again a tetragonal prism of type II (but of lower symmetry).
The ditetragonal prism yields again a ditetragonal prism, but of lower symmetry.
When hemimorphy is applied to the Basic Pinacoid (Figure 12) we obtain a pedion ( = monohedron). It is a single face, thus, like the pinacoid and the prisms, an open Form. It can close a prism (two pedions are needed for full closure) or monopyramid by combining with them (recall that only Forms belonging to the same Crystal Class can combine with each other, and recall also that open Forms cannot exist all by themselves but only in combinations resulting in closed structures). Of course two pedions will be generated by applying hemimorphy to a basic pinacoid, an upper pedion and a lower pedion. They are however each for themselves single, i.e. each one of them is an independent Form, and they can engage in a combinations, including combinations among themselves. So when for instance a hemimorphous prism is closed by two pedions (i.e. by a combination of a top pedion and a bottom pedion), these pedions do have the same crystallographic orientation (only their position is different), but because of the absence of a horizontal mirror plane the corresponding top and bottom faces will show some physical differences. For the two pedions see Figure 21. and 22.
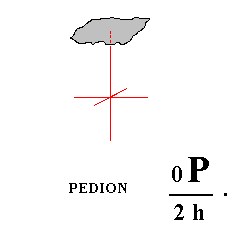
Figure 21. A Pedion or Monohedron, derived by hemimorphy from a Basic Pinacoid.
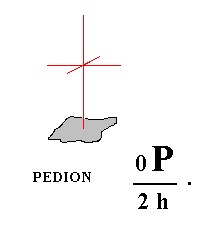
Figure 22. A second Pedion, also derived from a Basic Pinacoid by hemimorphy.
This concludes the derivation of the Forms of the Diteragonal-pyramidal Crystal Class by the Merohedric approach.
FACIAL APPROACH.
The Forms of this Class can also be derived from the basic faces (face types, relevant and compatible with the Tetragonal Crystal System).
These Faces are :
The stereographic projection of the symmetry elements of this Class will help us visualize the subjection of those faces to these symmetry elements :
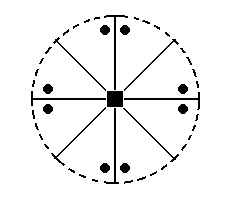
Figure 23. Stereogram of the symmetry elements of the Ditetragonal-pyramidal Class, and the (stereographic projection of the) face poles of the Form derived from the face with a general orientation, namely the face a : na : mc. The (dashed) circle is the projection plane, and the dashing indicates that this plane is not a mirror plane. Solid straight lines are vertical mirror planes.
The position of all the basic faces together in the projection plane of the stereographic projection is indicated in Figure 2a, and separately below. The symmetry elements of the present Class (as depicted in Figure 23) will multiply some faces, and leave unchanged others, depending on their orientation.
The face a : a : c (indicated in Figure 24) will, when subjected to the symmetry elements of the present Class, yield the type I tetragonal monopyramid of Figure 16, consisting of four faces, in virtue of the (effect of the) 4-fold rotation axis
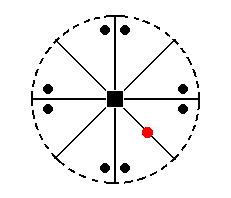
Figure 24. The position of the face (pole) a : a : c (red dot) in the stereographic projection of the (elements of the) Ditetragonal-pyramidal Class. The multiplication of the general face a : na : mc (black dots) is also indicated in order to clearly show the effect of the symmetry operations.
The stereographic projection of the type I tetragonal monopyramid is depicted in Figure 24aI, which shows the multiplication of the face a : a : c by the symmetry operations of the present Class (Ditetragonal-pyramidal Class).
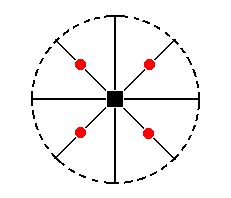
Figure 24aI. Stereogram of the Type I Tetragonal Monopyramid.
From the face a : a : -c (which is just a negative variant of a : a : c) we can derive the other
' half ', i.e. also a tetragonal pyramid, but with its apex directed downward. This Form is depicted in Figure 17. It is the lower half of the holohedric protopyramid. Its stereographic projection is depicted in Figure 24aII.
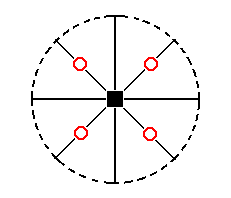
Figure 24aII. Stereogram of the other Type I Tetragonal Monopyramid. The face poles are depicted by (small red) circles to indicate that the faces are below the equatorial plane of the Form, i.e. below the plane of the secondary crystallographical axes.
The face a : ~a : c (indicated in Figure 25) will, when subjected to the symmetry elements of the present Class, yield a type II tetragonal monopyramid, i.e. a same pyramid as the one derived from a : a : c, but differing in its orientation (Figure 18). The face a : ~a : -c will give the same pyramid, but with its top down.
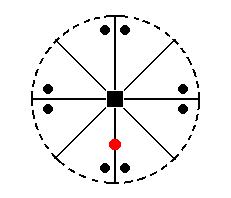
Figure 25. The position of the face (pole) a : ~a : c (red dot) in the stereographic projection (of the Ditetragonal-pyramidal Class).
To clearly show the workings of the symmetry operations of the Class, their effect upon the general face a : na : mc is shown (black dots).
The stereographic projection of the type II tetragonal monopyramid is depicted in Figure 25a.
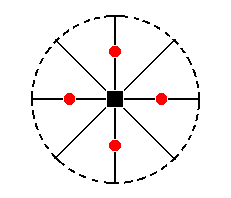
Figure 25a. Stereogram of the Type II Tetragonal Monopyramid ( = upper half of the holohedric Deuteropyramid, which is itself a bipyramid).
The face a : na : mc (indicated in Figure 27) will yield a ditetragonal monopyramid (Figure 19, for n = 2). The face is not parallel to any crystallographic axis. The mirror plane next to the face (see Figure 27) will generate a second face making an angle with the original face (See also 26). This pair of faces is then multiplied four times by the 4-fold rotation axis, resulting in the monopyramid mentioned.
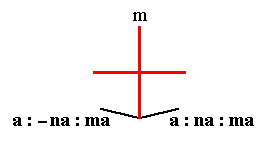
Figure 26. Equatorial plane of the tetragonal system of crystallographic axes. Depicted are the two secondary crystallographic axes, which coincide with vertical mirror planes. The face a : na : mc is reflected in the mirror plane m, and this reflection results in an additional face a : -na : mc, i.e. we now have two faces making an angle with each other.
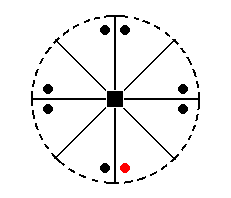
Figure 27. Position of the face (pole) a : na : mc (red dot) in the stereogram of the (elements of the) Ditetragonal-pyramidal Class. This face will be reflected and the resulting pair will be multiplied four times by the 4-fold rotation axis.
The stereographic projection of the ditetragonal monopyramid was already depicted in Figure 23, but is again shown in Figure 27a.
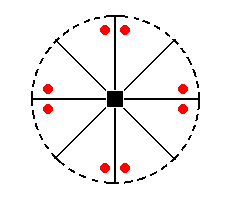
Figure 27a. Stereogram of the Ditetragonal Monopyramid.
The face a : a : ~c (indicated in Figure 28) is vertical. The 4-fold rotation axis will generate four such faces, and so a type I tetragonal prism (Figure 7) is generated. Although this prism has the same external shape as the one depicted in Figure 7, it does not have a (crystallographic) equatorial mirror plane, and its Naumann symbol is consequently no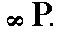t 
but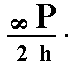 
, where "2h" indicates the hemimorphy involved.
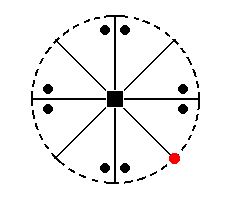
Figure 28. Position of the face (pole) a : a : ~c in the stereogram of the Ditetragonal-pyramidal Class.
The stereographic projection the Type I tetragonal prism is depicted in Figure 28a.
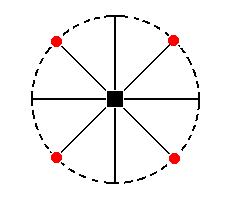
Figure 28a. Stereogram of the Type I Tetragonal (hemimorphous) Prism.
The face a : ~a : ~c (indicated in Figure 29) is vertically oriented and parallel to the east-west crystallographic axis. It will be multiplied four times by the 4-fold rotation axis resulting in a type II tetragonal prism (Figure 9), but again it lacks a horizontal mirror plane. Its Naumann symbol is therefore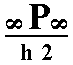 
.
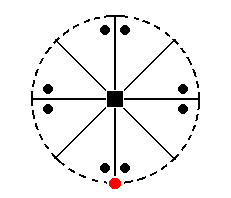
Figure 29. Position of the face (pole) a : ~a : ~c in the stereogram of the Ditetragonal-pyramidal Class.
The stereographic projection of the type II tetragonal prism is depicted in Figure 29a.
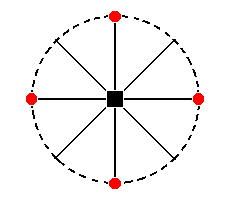
Figure 29a. Stereogram of the Type II (hemimorphous) Tetragonal Prism.
The face a : na : ~c (indicated in Figure 30) is vertical, it intersects both secondary axes, but the intercepts are different. Like the case of face a : na : mc the nearby vertical mirror plane generates two faces making an angle with each other, and this pair is being multiplied four times by the 4-fold rotation axis resulting in a ditetragonal prism, consisting of eight faces (Figure 11), but again it lacks an equatorial mirror plane. Its Naumann symbol is therefore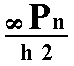 
.
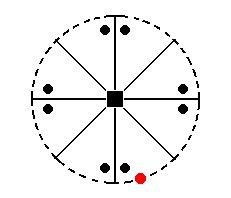
Figure 30. Position of face (pole) a : na : ~c in the stereographic projection of the Ditetragonal-pyramidal Class.
The stereographic projection of the ditetragonal prism is depicted in Figure 30a.
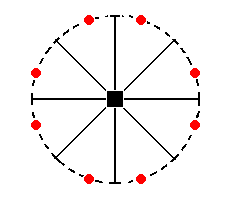
Figure 30a. The stereogram of a Ditetragonal (hemimorphous) Prism.
But of course a slightly different ditetragonal prism is possible (because the coefficient n of the face a : na : ~c can vary while still resulting in a ditetragonal prism). The stereographic projection of such a slightly different ditetragonal prism is shown in Figure 30aI.
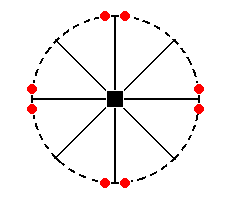
Figure 30aI. Stereogram of a slightly different Ditetragonal (hemimorphous) Prism.
The position of the generating face in the stereogram can vary along the arc between two mirror planes, resulting in several possible ditetragonal prisms.
Finally, the face ~a : ~a : c (indicated Figure 31) is horizontally oriented. It is not affected by any symmetry element of the present Class, so it remains a horizontal face, a pedion (Figure 21).
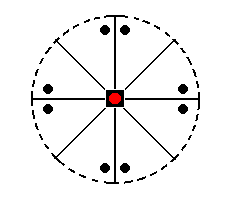
Figure 31. Position of the face (pole) ~a : ~a : c (red dot) in the stereogram of the Ditetragonal-pyramidal Class. It will not be affected by the symmetry operations of this Class (See Figure 31a).
The black dots still represent a general face a : na : mc, and show the workings of the symmetry elements.
The stereographic projection of the pedion (monohedron) is depicted in Figure 31a.
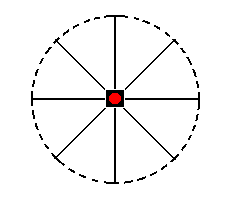
Figure 31a. Stereogram of the Pedion, one the Forms of the Ditetagonal-pyramidal Crystal Class.
This concludes our derivation of the Forms of the Ditetragonal-pyramidal Crystal Class (accomplished by two approaches).
As a real representative of this Class I can mention :
The pseudocubic mineral Diaboleite 2Pb(OH)2 . CuCl2 (STRÜBEL, 1977, p. 89).
To continue, klick HERE for Part Three.