back to Part One(Alternative name : Quadratic System)
Protopyramid
Deuteropyramid
Ditetragonal Bipyramid
Protoprism
Deuteroprism
Ditetragonal Prism
Basic Pinacoid
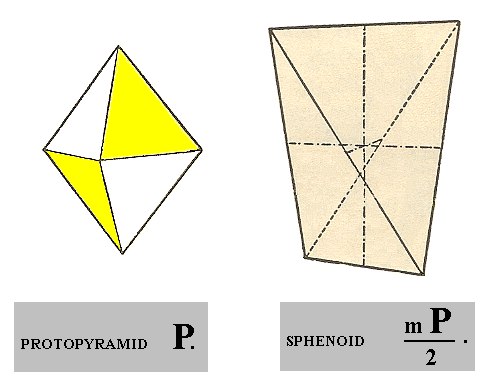
The protopyramid yields two sphenoids, i.e. tetrahedron-like Forms which are however not bounded by equilateral triangles but by isosceles triangles. See Figure 1.
Figure 1. From the (primary) Protopyramid (P) one can derive two Sphenoids.
The Sphenoid actually shown is generated from a derived Protopyramid (mP).
The deuteropyramid does not change its outer shape, so under this hemihedric it yields again a deuteropyramid, albeit one of lower symmetry. See Figure 2.
Figure 2. Because the suppressed mirror planes are pependicular to the faces of the Deuteropyramid it will not change its outer shape, but it will loose some symmetry, which will be evident when the crystal faces are physically examined.
The ditetragonal pyramid yields two tetragonal scalenohedra, which are congruent and only differ by their orientation. One of them is depicted in Figure 3.
Figure 3. The Ditetragonal Pyramid yields two Tetragonal Scalenohedra. In the Figure one such Scalenohedron is generated from the unstriped faces. Another one can be derived from the striped faces.
The protoprism (See Figure 7 in Part One) remains, with respect to its external shape, unchanged when this hemihedric is applied. So we obtain (again) a type I tetragonal prism. But of course its (crystallographic) symmetry is lowered accordingly. Its Naumann symbol is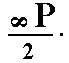 
. See Figure 4.
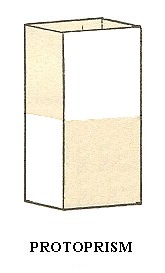
Figure 4. Protoprism, subjected to the sphenoidic hemihedric. Its external shape remains unchanged. This prism is drawn as a prism with top and bottom faces for reasons of clarity. These faces do not belong to the prism.
The deuteroprism (See Figure 9 in Part One) also remains the same with respect to its external shape. So after this hemihedric is applied we get again a Type II tetragonal prism as a Form of the present Class, but with lower symmetry. The Naumann symbol is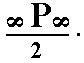 
. See Figure 5.
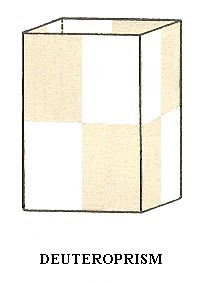
Figure 5. The Deuteroprism does not change its external shape when subjected to the sphenoidic hemihedric. Also this prism is drawn as a prism with top and bottom faces for reasons of clarity.
The ditetragonal prism (Figure 11 in Part One) also does not change its external shape when this hemihedric is applied. We again obtain a ditetragonal prism, but with a lower symmetry than the holohedric one. The Naumann symbol is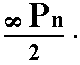 
. See Figure 6.
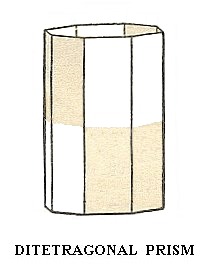
Figure 6. The Ditetragonal Prism does not change its extenal shape when subjected to this hemihedric. For reasons of clarity the prism is drawn as a prism with top and bottom faces.
The Final Form of this Class is the sphenoidic hemihedric basic pinacoid (parallelohedron). It derives from the holohedric basic Pinacoid (Figure 12 in Part One) by applying the sphenoidic hemihedric to it, resulting in a Form which consists again of two faces and is, like the prisms, an open Form. See Figure 7.
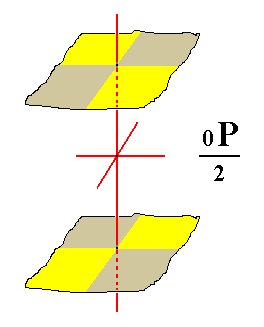
Figure 7. From the holohedric Basic Pinacoid is derived the sphenoidic hemihedric Basic Pinacoid.
The colored areas of the faces symbolize the suppression of two vertical mirror planes, namely the ones that together contain the horizontal crystallographic axes (the other two mirror planes bisecting the angles between these axes) remain. The coloring of the areas also symbolizes the suppression of the equatorial mirror plane, because below each yellow area of the upper face we find a brown area of the lower face, and below each brown area of the upper face we find a yellow area of the bottom face.
All these Forms can also engage in forming combinations with each other.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Tetragonal Crystal System) one by one to the symmetry operations of the present Class (the Tetragonal-scalenohedric Crystal Class).
Recall that the basic faces were the following :
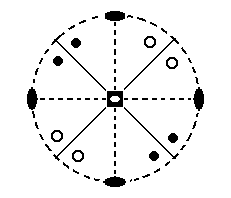
Figure 8. Stereographic projection of the symmetry elements of the Tetragonal-scalenohedric Crystal Class, and all the face poles of the most general of basic faces (i.e. all the face poles of the most general Form of the present Class). Solid dots refer to upper face poles (originating from faces above the equatorial plane of the crystal), small circles denote lower face poles (originating from faces below the equatorial plane of the crystal).
In the center of this projection we see the symbol for the 4-fold roto-inversion axis. Its operation is : a rotation of 900 followed by an inversion in a point on that axis, which means that the rotated motif appears (in virtue of the inversion) precisely at the opposite side of that point (See HERE in the general Essay on the Morphology of Crystals). Besides by the symbol in the figure (a white small ellipse in the center of a black square) it is also denoted by the sign 4* (In the crystallographic literature the asterisk is replaced by a score above the 4). In the present case this axis coincides with the main crystallographic axis, which is vertical [ In the stereographic projection it is (thought to be) perpendicular to the screen (or paper) -- in fact we see the projection of the two points of intersection of the axis with the projection sphere, one at the north pole, one at the south pole : these points are subsequently stereographically projected (from below and from above) onto the center of the projection plane].
The special quality of the 4* axis is evident when we consider the configuration of the motifs of a structure which has this axis. See Figure 8a.
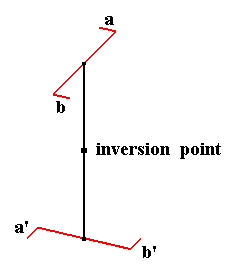
Figure 8a. The structure a b a' b' contains a vertical 4-fold roto-inversion axis. When we subject this structure to the axis' operation then a will end up at a' and b will end up at b', but at the same time a' will end up at a, and b' will end up at b. So the whole structure will be unchanged after the operation, i.e. the operation of the 4* axis transforms the structure onto itself, which is equivalent to saying that the structure has 4* symmetry.
The operation of this same axis can also be considered as a rotation of 900 directly followed by a reflection in the equatorial plane. One can check in the Figure that the same effect will result : The structure will be transformed onto itself.
It is evident that also a rotation of 1800 about that axis will transform the structure onto itself, so we have to do with a special 2-fold rotation axis.
Further we see, in the stereogram (Figure 8), two horizontal 2-fold rotation axes perpendicular to each other, and indicated by two small solid ellipses for each axis connected by a dashed line (if this line were solid than such a line would indicate a vertical mirror plane in which the axis lies). Next we see two vertical mirror planes, represented by solid lines. They bisect the angles between the 2-fold rotation axes. The circumference of the projection plane is dashed, which means that the projection plane is not (also) a mirror plane.
We are now ready to successively derive the Forms of the present Class by subjecting the above listed basic faces one by one to the symmetry elements of the Class. Because these symmetry elements are indicated in the stereogram (Figure 8), we can insert a face in that stereogram (i.e. we can insert the projection of a face pole -- representing the face concerned -- into the stereogram) and see what happens when we let the symmetry elements do their work on it.
We start with the face a : a : c.
Its position in the stereogram is indicated by a red dot in Figure 9.
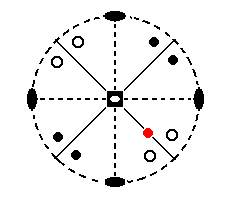
Figure 9. The position of the (projected) face (pole) a : a : c in the stereogram of the symmetry elements of the Tetragonal-scalenohedric Crystal Class is indicated by a red dot.
Also indicated (black dots and small circles) are all the face poles representing the (complete) Form generated from the general face a : na : mc, in order to clearly see the effect of the symmetry elements. Dots represent upper faces, small circles represent lower faces.
It is a face that is not perpendicular to any crystallographic axis. It is the unit face for the Tetragonal Crystal System, and can be seen as the upper right front face of a tetragonal bipyramid. When subjected to the 4* axis, a copy of it is rotated 900 clockwise about the axis, in this case (rotated) about the main crystallographic axis, and then inverted through the origin of the system of crystallographic axes, the result will be a lower face. When this latter face is in turn subjected to the 4* axis, i.e. be rotated 900 and then inverted through the origin, the result will be another upper face. Subjecting this face in turn to the 4* axis will generate another lower face. When we finally subject this face in turn to the 4* axis we will obtain a face which we already had, namely our initial face.
The configuration of faces so obtained, is a sphenoid (Figure 1) (also called a disphenoid). The mirror planes and the 2-fold rotation axes are implied by the 4* axis if the four motifs involved are themselves symmetric. The 4* axis itself (see Figure 8a) does not demand such a symmetry of the motifs. When indeed the motifs are themselves symmetric then their configuration according to the 4* axis looks as in the next Figure, and this configuration complies with the symmetry content of the present Class :
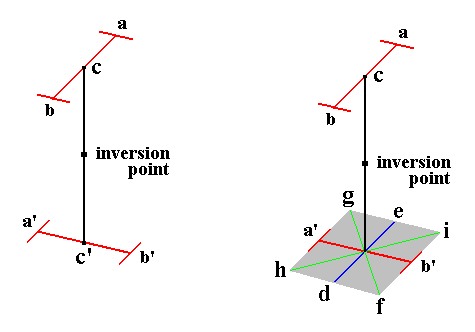
Figure 8b. A configuration of symmetrical motifs according to a 4-fold roto-inversion axis.
Because of the symmetry of the motifs themselves, additional symmetries (for the whole object, consisting of four motifs) are generated (i.e. implied), namely two mirror planes, one that goes through a' b' c and one that goes through a b c', and two 2-fold rotation axes, going through the inversion point, one lying in the plane f g c and the other in the plane h i c [If we rotate the whole object vertically by 450 then we get the same orientation of the symmetry elements as depicted in the corresponding stereographic projection ].
Let us develop in stages the stereographical projection of the resulting (sphenoidic hemihedric) sphenoid in the next Figures. We'll start with the stereographic projection of the initial face, namely the face a : a : c :
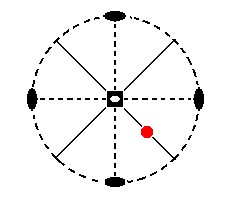
Figure 9a. Position of the face (pole) a : a : c in the stereographic projection of the symmetry elements of the Tetragonal-scalenohedric Crystal Class.
[We do not depict here, as in the next three Figures, the face poles of the complete general Form (which were after all only included for reasons of clarity with respect to the workings of the symmetry elements of the Class which could then easily be read off from their configuration ].
From the initial face a second face is generated, see Figure 9b.
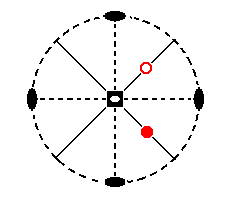
Figure 9b. Stereogram of the initial face a : a : c and of the second generated face, generated by the action of the 4* axis.
A dot represents an upper face, a small circle a lower one.
In generating this second face by the action of the 4* axis we rotatate it 900 clockwise about the axis (which coincides with the crystallographic main axis) and then invert it through the inversion point (the middle of the crystallographic main axis). This results in a lower face, meaning that its face pole lies on the lower hemisphere of the projection sphere (and is (then) upwardly projected, i.e. it is projected from below, onto the projection plane).
Next we will generate the third face. See Figure 9c.
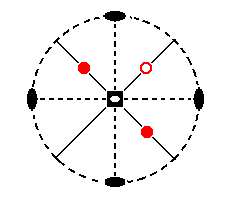
Figure 9c. When we rotate the above generated lower face (small red circle) 900 clockwise about the main crystallographic axis and then invert it through the inversion point, a third face is generated, which is an upper face.
Next we will generate the fourth face. See Figure 9d.
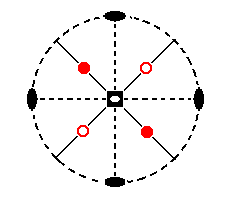
Figure 9d. When we rotate this third face (red dot in the upper left quadrant of the stereographic projection of Figure 9c) clockwise 900 about the main crystallographic axis and then invert it through the inversion point, then a fourth face, a lower face, will be generated.
When we repeat this operation on that fourth face we'll get the first face (the initial face) again. So no new faces are obtained anymore by further repeating the operation of the 4* axis. The Form thus obtained, consisting of four faces, is the Sphenoid.
The face a : ~a : c (indicated in Figure 10) is parallel to the east-west crystallographic axis, and makes an angle with the main axis.
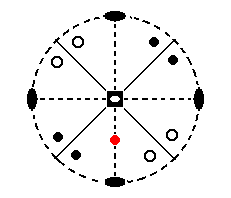
Figure 10. Projection (red dot) of the face (pole) a : ~a : c in the stereogram of the Tetragonal-scalenohedric Class (The face poles of the general Form are also indicated).
Because some symmetry elements imply others we do not have to involve all the symmetry elements when we derive a Form from a face. But of course the Form so derived must comply with all the symmetry elements of the Class.
So let us see what Form derives from the face a : ~a : c.
The nearest 2-fold rotation axis (vertical in Figure 10) will generate a second face, which meets the initial face from below. One mirror plane will duplicate this pair and the other mirror plane will duplicate the result. So we will end up with a tetragonal bipyramid which has an orientation such that it belongs to type II (See Figure 2).
The stereographic projection of this type II (sphenoidic hemihedric) tetragonal bipyramid is depicted in Figure 10a.
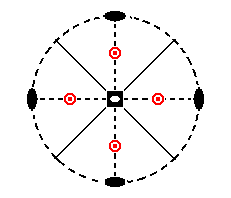
Figure 10a. Stereogram of the Type II (sphenoidic hemihedric) Tetragonal Bipyramid.
The face a : na : mc is the general face. Its position in the stereographic projection is depicted in Figure 11.
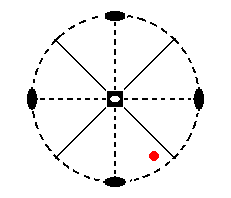
Figure 11. Stereogram of the symmetry elements of the Tetragonal-scalenohedric Class, and the position of the face a : na : mc (red dot).
The nearby mirror plane will generate a second face, making an angle with the initial face. When we subject this pair to the 4-fold roto-inversion axis, we will obtain a tetragonal scalenohedron (Figure 3).
We can develop its stereographic projection in the same way as we did with respect to the sphenoid, according to the next Figures :
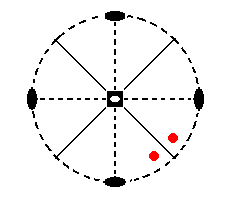
Figure 11a. In virtue of the nearby mirror plane the initial face is duplicated, resulting in an upper face pair.
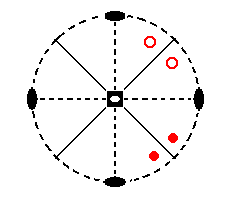
Figure 11b. (A copy of) this upper face pair is now subjected to the 4* axis, which means that it is rotated clockwise 900 about the main crystallographic axis and then inverted through the origin of the system of crystallographic axes. This results in a second face pair, a lower face pair.
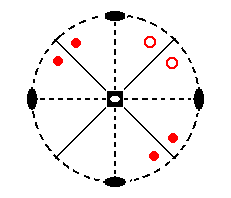
Figure 11c. When we subject this latter face pair in turn to the 4* axis we will rotate (a copy of) it clockwise 900 and invert it through the origin of the crystallographic axes resulting in a third face pair, an upper face pair.
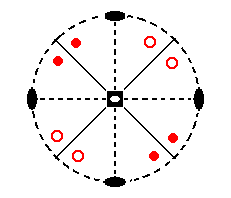
Figure 11d. When we, finally do the same with the latter face pair we will obtain a fourth face pair. Further repetition of these operations does not yield new faces anymore. These four face pairs together form the Tetragonal Scalenohedron of which the stereogram is depicted here.
The face a : a : ~c (See Figure 12) is vertically oriented. It appears therefore in the stereographic projection at the periphery of the projection plane. It cuts off equal pieces of the horizontal crystallographic axes.
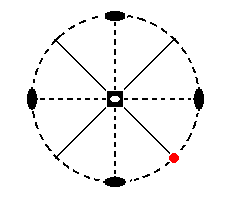
Figure 12. Position of the face (pole) a : a : ~c in the stereographic projection of the symmetry elements of the Tetragonal-scalenohedric Crystal Class (I have not indicated the multiplication of the pole of the general face a : na : mc anymore, which had served earlier to show the workings of the symmetry elements more clearly, because these workings will by now be clear to the reader from inspecting just the stereogram of the symmetry elements only).
The face is not affected by the mirror plane that is perpendicular to it. But the other mirror plane duplicates it. So we have now two parallel faces. When we next apply to this face pair the 4-fold roto-inversion axis (4*) a copy of each face is turned 900 about that axis and immediately inverted through the origin of the crystallographic axes, resulting in new opposite lower faces. But because these 'lower' faces are vertical they are identical with their upper counterparts, i.e. with their upwardly directed extensions. So the result is a tetragonal prism of type I (Figure 4), but of course having a lower symmetry than the holohedric protoprism.
Because the effect of the 4-fold roto-inversion axis is equivalent to a rotation of 900 directly followed by a reflection with respect to a horizontal (equatorial) mirror plane (notice that this plane, all by itself, is not a symmetry element of the present Class, only its combination with a 4-fold axis exists as such a symmetry element), we can also visualize the generation of the tetragonal prism in the following way :
A copy of the parallel face pair (generated as described) is turned 900 and then directly reflected with respect to the mentioned equatorial mirror plane. Because the faces are vertical this reflection will not affect them, and we now already possess the prism.
The stereographic projection of the (sphenoidic hemihedric) type I tetragonal prism is depicted in Figure 12a.
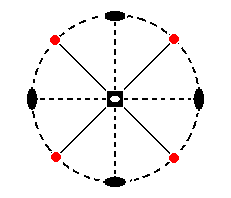
Figure 12a. Stereogram of the (sphenoidic hemihedric) type I Tetragonal Prism.
The face a : ~a : ~c is vertical and is parallel to the east-west crystallographic axis. Its stereographic projection is located at the periphery of the projection plane as figure 13 indicates.
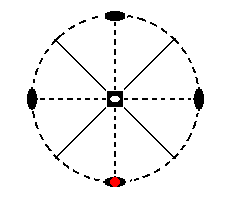
Figure 13. Stereogram of the face (pole) a : ~a : ~c (red dot).
One mirror plane duplicates this face resulting in a pair of faces making an angle (smaller than 1800) with each other. The other mirror plane duplicates this pair resulting in a tetragonal prism of type II.
The stereographic projection of the (sphenoidic hemihedric) Type II tetragonal prism is depicted in Figure 13a.
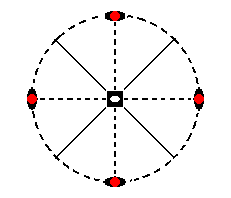
Figure 13a. Stereogram of the Type II Tetragonal Prism.
The face a : na : ~c is vertical. It cuts off unequal pieces from the horizontal axes.
n (like in the case of the face a : na : mc) can vary between 1 and infinity. Its position in the stereographic projection of the symmetry elements of the present Class is depicted in Figure 14.
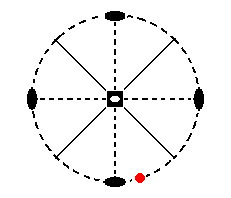
Figure 14. Stereogram of the face (pole) a : na : ~c, and of the symmetry elements of the Tetragonal-scalenohedric Crystal Class.
This face is duplicated by one of the mirror planes resulting in two faces making an angle. This pair is rotated 900 and reflected with respect to the equatorial plane. But because this reflection has no effect the axis works like an ordinary 4-fold rotation axis and multiplies the face pair four times, resulting in a (sphenoidic hemihedric) ditetragonal prism. Its stereographic projection is pictured in Figure 14a.
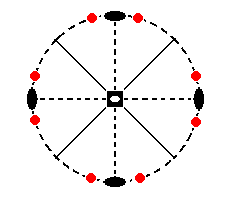
Figure 14a. Stereogram of the (sphenoidic hemihedric) Ditetragonal Prism.
Finally the face ~a : ~a : c is horizontally oriented, so its stereographic projection will place it in the center of the projection plane, as indicated in Figure 15.
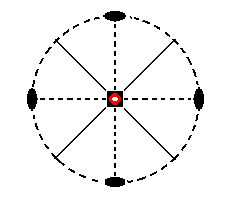
Figure 15. Position of the face (pole) (red dot in the center) ~a : ~a : c in the stereogram of the symmetry elements of the Tetragonal-scalenohedric Crystal Class.
The mirror planes have no effect on that face, but the 2-fold rotation axes generate a second face parallel to the initial one. The 4-fold roto-inversion axis has the same effect, its operation can be described by either a rotation of 900 directly followed by an inversion, or a rotation of 900 directly followed by a reflection in the equatorial plane. Following this last prescription we observe that the rotation does not have an effect upon the face, but the reflection will, and so a second face is generated parallel to the initial one. This pair of faces is called a basic pinacoid. Its stereographic projection is the same as the one in Figure 15, but in this case there are two projections superposed upon each other, one from above and one from below. See Figure 15a.
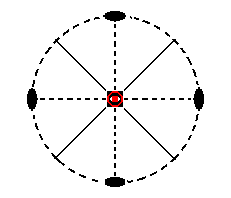
Figure 15a. Stereogram of the sphenoidic hemihedric Basic Pinacoid.
Red dot : upper face. Red (small) circle : lower face.
This concludes our exposition of the Tetragonal-scalenohedric Crystal Class.
To continue, klick HERE for Part Four.