back to Part One(Alternative name : Quadratic System)
Protopyramid
Deuteropyramid
Ditetragonal Bipyramid
Protoprism
Deuteroprism
Ditetragonal Prism
Basic Pinacoid
The protopyramid yields again a type I tetragonal bipyramid as is evident from Figure 16.

Figure 16. When we apply the pyramidal hemihedric to the Protopyramid, we obtain again a Type I Tetragonal Bipyramid, but with corresponding lower symmetry. It is accordingly a Type I pyramidal hemihedric Tetragonal Pyramid. The brackets are used to distinguish this hemihedric from others.
The deuteropyramid yields again a type II tetragonal bipyramid as is evident from Figure 17.
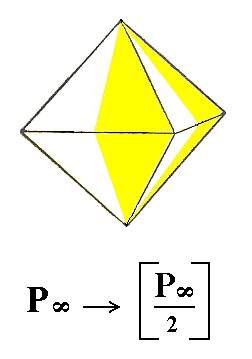
Figure 17. The Deuteropyramid, when subjected to the pyramidal hemihedric, yields again a Type II Tetragonal Bipyramid. It is accordingly a pyramidal hemihedric Type II Tetragonal Bipyramid.
The ditetragonal bipyramid, when subjected to this hemihedric, yields two tritopyramids, i.e. pyramids of type III. These pyramids have the same shape as the type I and II have, and are distinguished only by their orientation. In Figure 18 it is evident that the holohedric ditetragonal bipyramid admits of two tritopyramids, depending on which faces (the striped ones or the unstriped ones) are let to survive.
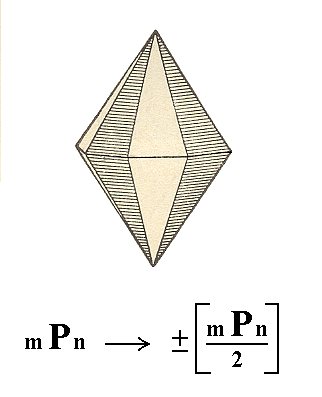
Figure 18. Because of the suppression of all the vertical mirror planes ( = to apply the pyramidal hemihedric) the Ditetragonal Bipyramid looses half its faces (because the suppressed mirror planes are not perpendicular to any face) resulting in either a Tetragonal Tritopyramid constituted of the unstriped faces, or a Tetragonal Tritopyramid constituted of the striped faces.
For a better understanding it is probably useful to compare the several pyramids, the type I, II and III tetragonal (bi)pyramids, and the ditetragonal (bi)pyramids, by means of (comparing) their respective equatorial planes. See Figures 19, 20 and 21.
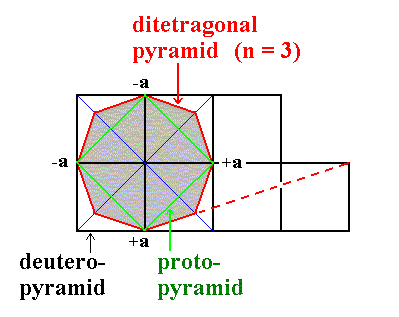
Figure 19. Equatorial planes of Protopyramid (= type I pyramid), Deuteropyramid (= type II pyramid) and Ditetragonal Pyramid (n = 3).
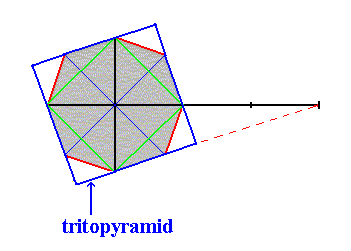
Figure 20. Derivation of one of the Tritopyramids (= type III pyramid) from the Ditetragonal Pyramid. Like the Type I and Type II Pyramids the equatorial section of the Tritopyramid is a square.
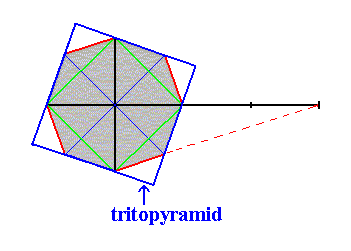
Figure 21. Derivation of the other Tritopyramid (= type III pyramid) from the same Ditetragonal Pyramid. Like the Type I and Type II pyramids the equatorial section of a Tritopyramid is a square.
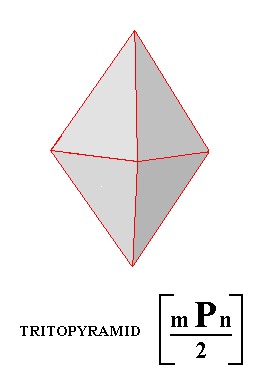
Figure 22. The Tritopyramid, derived from the striped faces of the Ditetragonal Pyramid of Figure 18.
The protoprism does not change its external shape, when subjected to this hemihedric. It becomes a pyramidal hemihedric type I tetragonal prism. See Figure 23.
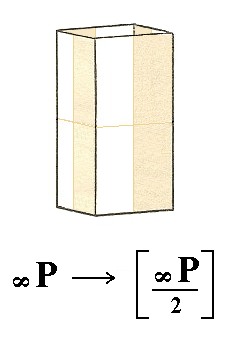
Figure 23. The Protoprism does not change its shape but looses some symmetry.
The deuteroprism does also not change its external shape when subjected to the pyramidal hemihedric, but looses some symmetry. See Figure 24.
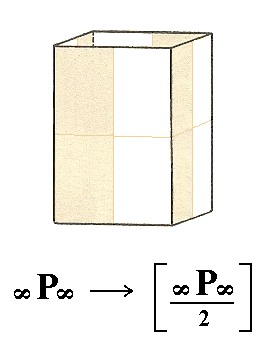
Figure 24. The Deuteroprism becomes a pyramidal hemihedric Type II Tetragonal Prism.
The ditetragonal prism does change its shape when subjected to the pyramidal hemihedric. It becomes a tetragonal tritoprism. See Figure 25, 26 and 27.
The tetragonal tritoprism is generated in a way analogous to the tritopyramid (Figures 19, 29 and 21).
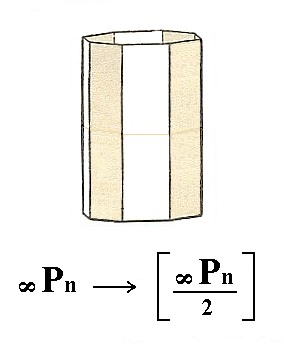
Figure 25. The Ditetragonal Prism undergoing pyramidal hemihedric, which results in two Tritoprisms.
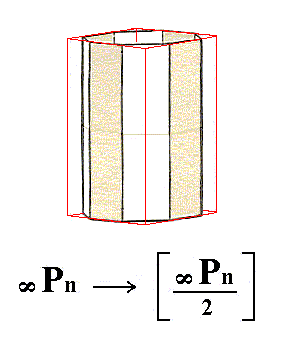
Figure 26. Actual construction of a Tritoprism by letting the colored faces of the Ditetragonal Prism extend, till they meet.
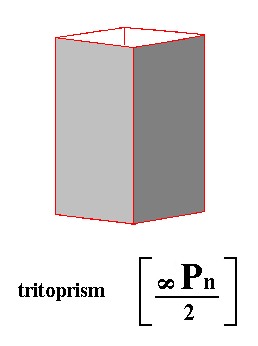
Figure 27. Tritoprism, as a result of the construction in Figure 26.
The final holohedric Form to be subjected to the pyramidal hemihedric is the basic pinacoid. The suppression of all the vertical mirror planes does not have any effect on the external shape of the basic pinacoid, so we will obtain a pyramidal hemihedric basic pinacoid. See Figure 28.
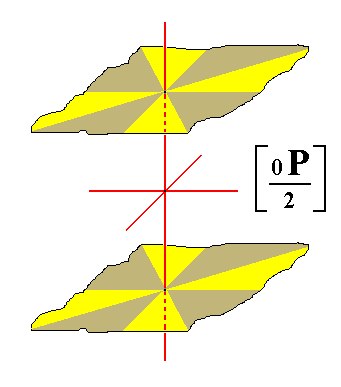
Figure 28. The pyramidal hemihedric Basic Pinacoid.
The coloring of the areas symbolizes the suppression of all the vertical mirror planes. Both faces remain however (after applying this hemihedric). The non-suppression of the vertical mirror plane is also symbolized by the colors : Vertically below each yellow area of the upper face we find a yellow area of the lower face, and below each brown area of the upper face we find a brown area of the lower face.
This concludes the derivation of the Forms of the Tetragonal-bipyramidal Class by means of the Merohedric Approach.
All these Forms can engage in combinations.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Tetragonal Crystal System) one by one to the symmetry operations of the present Class (the Tetragonal-bipyramidal Crystal Class).
Recall that the basic faces were the following :
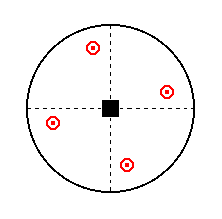
Figure 29. Stereographic projection of the symmetry elements of the Tetragonal-bipyramidal Crystal Class, and of the faces of the most general Form, a Tetragonal Bipyramid.
The face a : a : c is the unit face of the Tetragonal Crystal System. It therefore cuts off equal pieces (by definition unit distances from the origin of the axes) from the horizontal crystallographic axes and is inclined in such a way (by definition) as to cut off a piece of unit length from the vertical axis. Its stereographic projection is depicted in Figure 30.
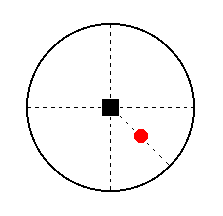
Figure 30. Position of the face a : a : c in the stereographic projection of the symmetry elements of the Tetragonal-bipyramidal Crystal Class.
This face is multiplied four times in virtue of the 4-fold rotation axis, and the result (four faces, forming an open monopyramid, is reflected with respect to the mirror plane coinciding with the equatorial plane, resulting in a (pyramidal hemihedric) Type I tetragonal bipyramid (Figure 16). Its stereographic projection is depicted in Figure 30a.
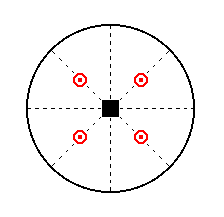
Figure 30a. Stereogram of the pyramidal hemihedric Type I Tetragonal Bipyramid.
Recall that a mirror plane in a stereographic projection is always depicted as a solid line, either a circle or a straight line. In the stereogram of this figure the only mirror plane is the equatorial plane (solid circle). The north-south and east-west dashed lines, as they appear in the stereogram, are in this case not symmetry elements (i.e. also not rotation axes). They represent the equatorial crystallographic axes. The other dashed lines are just visual aids.
The face a : ~a : c is parallel to the east-west crystallographic axis. It cuts off unit distances from the north-south crystallographic axis and from the vertical crystallographic axis. Its position in the stereographic projection is depicted in Figure 31.
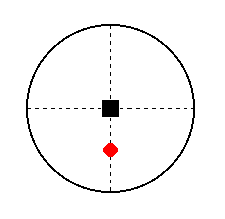
Figure 31. The position of the face a : ~a : c in the stereogram of the Tetragonal-bipyramidal Crystal Class.
This face is multiplied four times by the 4-fold rotation axis, resulting in an open monopyramid. Then this pyramid is reflected by the equatorial mirror plane resulting in a (pyramidal hemihedric) Type II tetragonal bipyramid (Figure 17). See Figure 31a.
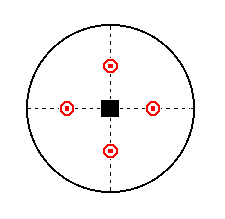
Figure 31a. Stereogram of the pyramidal hemihedric Type II Tetragonal Bipyramid.
The face a : na : mc is the most general face, the intercepts with respect to the east-west and the vertical crystallographic axes are different from the respective unit intercepts. It has an arbitrary position in the stereographic projection. See Figure 32.
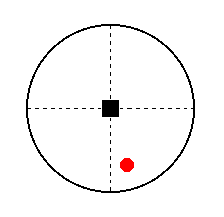
Figure 32. Position of the face a : na : mc in the stereogram of the Tetragonal-bipyramidal Crystal Class.
This face is multiplied four times in virtue of the 4-fold rotation axis, resulting in a tetragonal monopyramid. This pyramid is then reflected with respect to the equatorial mirror plane resulting in a (pyramidal hemihedric) type III tetragonal bipyramid (tritopyramid) (Figure 22). The stereogram of this tritopyramid is depicted in Figure 32a.

Figure 32a. Stereogram of the Tetragonal Tritopyramid.
The face a : a : ~c is vertical, so in the stereographic projection it lies on the periphery of the projection plane. See Figure 33.
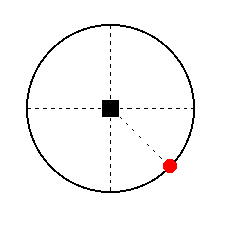
Figure 33. Position of the face a : a : ~c in the stereographic projection of (the symmetry elements of) the Tetragonal-bipyramidal Crystal Class.
This face is multiplied four times in virtue of the 4-fold rotation axis. The equatorial mirror plane has no further effect on the result. So we obtain a (pyramidal hemihedric) type I tetragonal prism (Figure 23). The stereographic projection of this prism is depicted in Figure 33a.
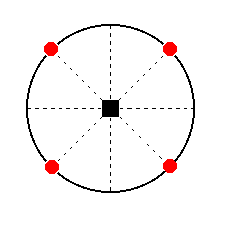
Figure 33a. Stereogram of the pyramidal hemihedric Type I Tetragonal Prism.
The face a : ~a : ~c is also vertical. It is moreover parallel to the east-west crystallographic axis. Its position in the stereographic projection is depicted in Figure 34.
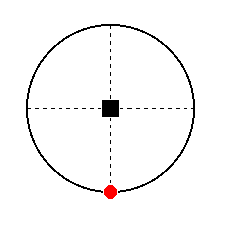
Figure 34. Position of the face a : ~a : ~c in the stereographic projection of (the symmetry elements of) the Tetragonal-bipyramidal Crystal Class.
The 4-fold rotation axis generates a prism when applied to this face. Again the equatorial mirror plane has no effect. The result is a (pyramidal hemihedric) Type II tetragonal prism. Its stereographic projection is depicted in Figure 34a.
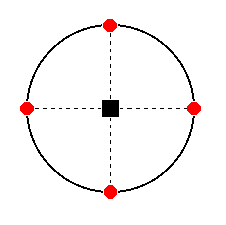
Figure 34a. Stereogram of the pyramidal hemihedric Type II Tetragonal Prism.
The face a : na : ~c is vertical. From the east-west crystallographic axis it cuts off a piece different from the unit piece.
n can have values greater than 1 and smaller than infinity [if it is smaller than 1, then we multiply it with a factor such that it becomes 1, multiply the other coefficients with the same factor -- recall that only proportions count -- and rotate the system of axes 900 clockwise about the vertical axis, in order to make the axis, of which the cut-off piece is now equal to 1, the north-south crystallographic axis].
The position of this face in the stereographic projection is shown in Figure 35.
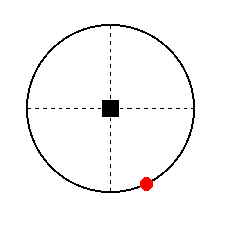
Figure 35. Position of the face a : na : ~c in the stereographic projection of (the symmetry elements of) the Tetragonal-bipyramidal Crystal Class..
This face is multiplied four times, resulting in a Type III tetragonal prism ( = tetragonal tritoprism), the equatorial mirror plane does not add anything further.
The stereographic projection of the (pyramidal hemihedric) type III tetragonal prism is shown in Figure 35a.
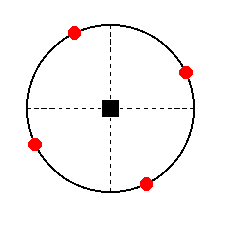
Figure 35a. Stereogram of the Tetragonal Tritoprism.
The face ~a : ~a : c is horizontal. Its position in the stereogram of the present Class is shown in Figure 36.
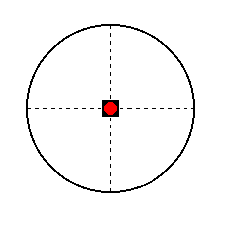
Figure 36. Position (red dot) of the face ~a : ~a : c in the stereogram of (the symmetry elements of) the Tetragonal-bipyramidal Crystal Class.
The 4-fold rotation axis has no effect upon it, but the horizontal mirror plane does. So we obtain a (pyramidal hemihedric) basic pinacoid. It consists of two horizontal parallel faces. Its stereographic projection is shown in Figure 36a.
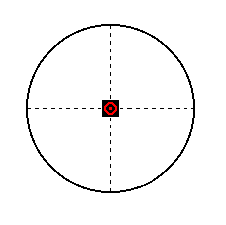
Figure 36a. Stereogram of the pyramidal hemihedric Basic Pinacoid. Its two faces coincide in the projection as indicated.
This concludes our derivation (by means of two approaches) of the Forms of the Tetragonal-bipyramidal Crystal Class (= Pyramidal Hemihedric Division).
To continue, klick HERE for Part Five.