back to Part One(Alternative name : Quadratic System)
The symmetry content of this Class is :
In doing so we first show (again) the relevant pyramidal hemihedric Form, and then show the derivation of the hemimorphous Form from it.
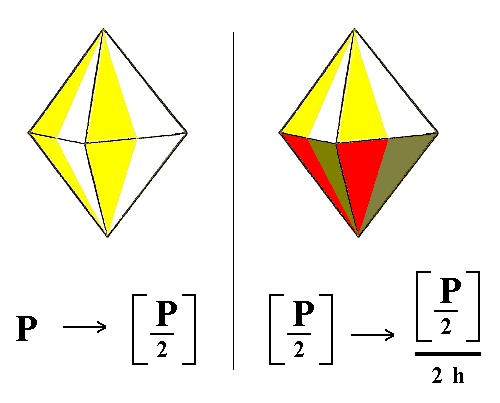
1. Derivation from the pyramidal hemihedric Type I Tetragonal Bipyramid.
Figure 1.
Left image.
The pyramidal hemihedric Type I Tetragonal Bipyramid, derived from the holohedric Protopyramid.
Right image.
Applying hemimorphy to the pyramidal hemihedric Type I Tetragonal Bipyramid.
The Naumann symbol clearly shows the repeated hemihedric (pyramidal hemihedric and hemimorphy), i.e. the successive application of two hemihedrics to a holohedric Form.
The "h" in 2 h signifies the second hemihedric (being applied), namely the hemimorphy.
The hemimorphy demands the suppression of the equatorial mirror plane which was present in the pyramidal hemihedric Form, which implies that in the derivation we must mark the bottom faces in such a way that they are distinguished from any upper face, garanteeing the absence of the equatorial mirror plane. See Figure 1, right image.
The result is a Type I tetragonal monopyramid possessing no mirror planes whatsoever.
Of course two are possible, the upper half of the initial bipyramid and the lower half of that pyramid. They are independent of each other and can occur together as a combination. But also the one or the other can combine with other Forms of this Class. The monopyramids are open Forms, so a single monopyramid cannot occur all by itself.
Figure 2 shows them.
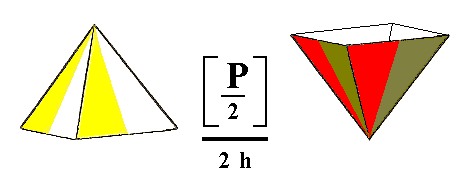
Figure 2. The two possible Tetragonal Monopyramids. Forms of the Tetragonal-pyramidal Crystal Class.
2. Derivation from the pyramidal hemihedric Type II Tetragonal Bipyramid.
The hemimorphy suppresses the equatorial mirror plane, resulting in the suppression of either the lower faces or the upper ones. So we obtain two hemimorphous type II tetragonal monopyramids. See Figure 3.
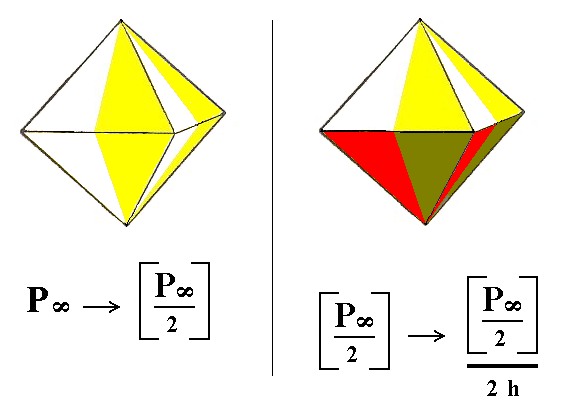
Figure 3. The derivation of the Monopyramids by subjecting a Type II Tetragonal Bipyramid to hemimorphy. It will result in two monopyramids, as depicted in Figure 4.
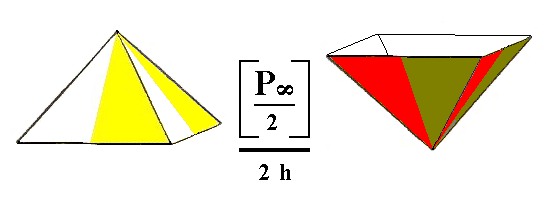
Figure 4. Two independent Tetragonal Monopyramids, originated by hemimorphy applied to a pyramidal hemihedric Type II Tetragonal Bipyramid.
3. Derivation from the pyramidal hemihedric Type III Tetragonal Bipyramid, the Tetragonal Tritopyramid.
Also here the suppression of the equatorial mirror plane ( = application of hemimorphy) results in two independent type III monopyramids, one of which is shown in Figure 5.
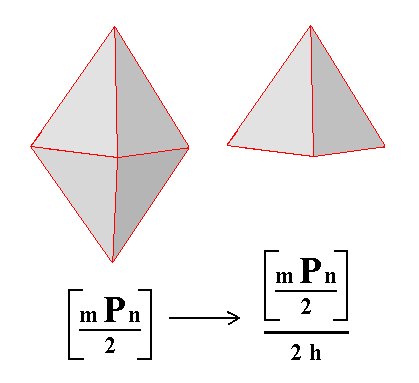
Figure 5. Derivation of the Type III monopyramid from the pyramidal hemihedric Type III Bipyramid by applying hemimorphy. This monopyramid is exactly identical to the above monopyramids of type I and type II, except its orientation with respect to the crystallographic axes. Also here we can indicate the absence of (vertical) mirror planes as done in the next Figure.
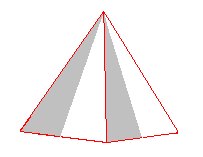
Figure 6. The hemimorphic Type III Tetragonal Pyramid. Absence of vertical mirror planes is indicated.
4. Derivation from the pyramidal hemihedric Type I Tetragonal Prism.
The suppression of the equatorial mirror plane ( = applying hemimorphy) does not have any effect on the external shape of the prism, but of course it looses some symmetry. So we obtain again a type I tetragonal prism. See Figure 7.
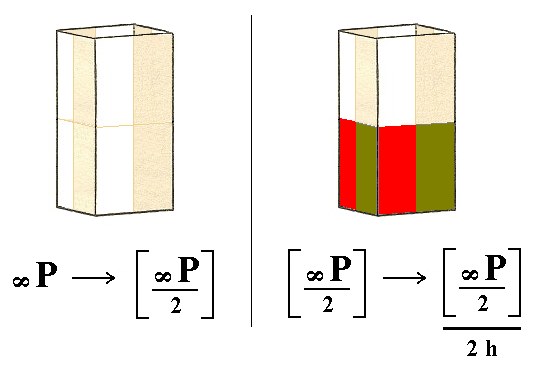
Figure 7. Derivation of the hemimorphous Type I Tetragonal Prism from the pyramidal hemihedric Type I Tetragonal Prism. The absence of vertical as well as of horizontal mirror planes is indicated.
5. Derivation from the pyramidal hemihedric Type II Tetragonal Prism.
Applying hemimorphy to the pyramidal hemihedric type II tetragonal prism gives again rise to a type II tetragonal prism but with lower symmetry. See Figure 8.
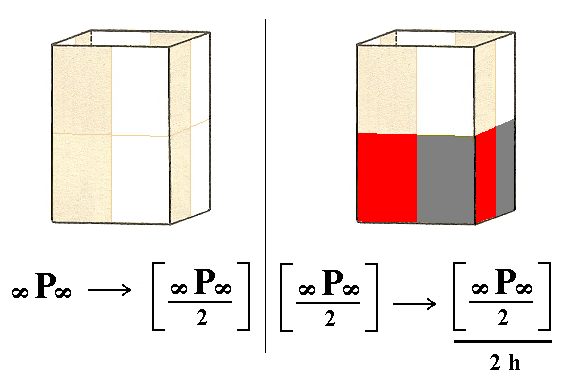
Figure 8. Getting a hemimorphous Type II Tetragonal Prism from a pyramidal hemihedric Type II Tetragonal Prism. The absence of all the mirror planes is indicated.
6. Derivation from the pyramidal hemihedric Type III Tetragonal Prism, the Tetragonal Tritoprism.
Applying hemimorphy to the tritoprism does not change its external shape, but lowers its (crystallographic) symmetry accordingly. See Figure 9.
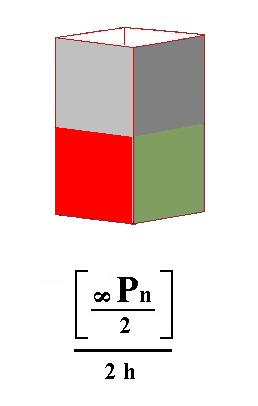
Figure 9. The pyramidal hemihedric Tritoprism has become a hemimorphous (pyramidal hemihedric) Type III Tetragonal Prism, having no mirror planes whatsoever, despite the fact that the Figure suggests some vertical mirror planes.
7. Derivation from the pyramidal hemihedric Basic Pinacoid.
The basic pinacoid consists of two parallel faces. When hemimorphy is applied to this Form we obtain two independent halves of it, two pedions. So this new Form, the pedion, is just one face. The derivation of one such pedion is depicted in Figure 10 and 10a.
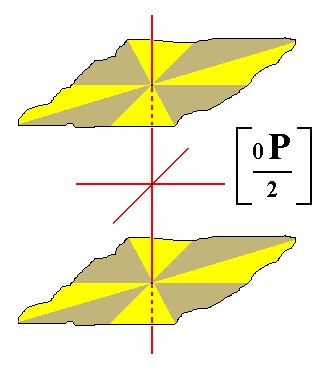
Figure 10. The pyramidal hemihedric Basic Pinacoid, from which the Pedion is derived by hemimorphy.
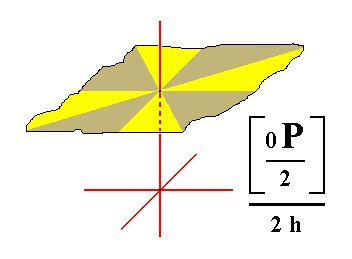
Figure 10a. A Pedion (monohedron), derived from the pyramidal hemihedric Basic Pinacoid.
All these Forms can engage in combinations.
As an example could serve the combination of Forms in crystals of the mineral Wulfenite (BRUHNS, 1912, p. 63). See Figure 11. On top we see the primary protopyramid (here a monopyramid)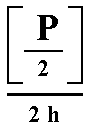 
(p in the Figure), of which the corners are cut off
in an oblique fashion by the tritoprism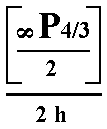 
(r in the Figure). At the bottom the
polar corner of the other monopyramid 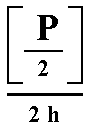(p' in the Figure) is cut off by a pedion.
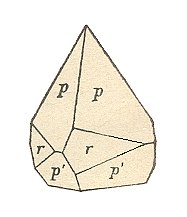
Figure 11. Combination of two Tetragonal Type I Pyramids (p and p') and a Tritoprism (r).
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Tetragonal Crystal System) one by one to the symmetry operations of the present Class (the Tetragonal-pyramidal Crystal Class).
Recall that the basic faces were the following :
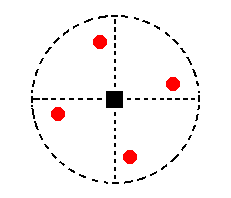
Figure 12. Stereogram of the symmetry elements of the Tetragonal-pyramidal Crystal Class and of all the face poles of the most general Form.
The face a : a : c is the unit face of the Tetragonal Crystal System. Its position in the stereographic projection of the symmetry elements of the present Class is shown in Figure 13.
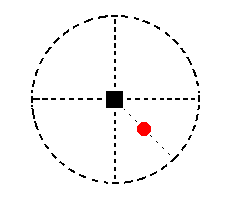
Figure 13. Stereogram of the symmetry elements of the Tetragonal-pyramidal Crystal Class and the position of the face a : a : c.
This face a : a : c generates, when subjected to the symmetry elements of the present Class, consisting of a 4-fold rotation axis only, a type I tetragonal monopyramid (Figure 2). Its stereographic projection is depicted in Figure 13a.
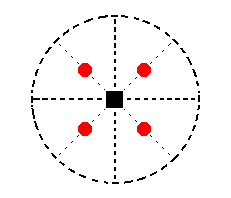
Figure 13a. Stereogram of the hemimorphous Type I Tetragonal Pyramid.
The face a : ~a : c is parallel to the east-west crystallographic axis and cuts off a unit piece from the main crystallographic axis. Its position is depicted in Figure 14.
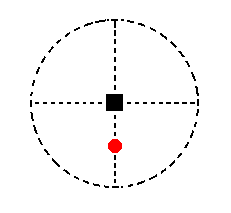
Figure 14. Position if the facea : ~a : c in the stereographic projection of the symmetry elements of the Tetragonal-pyramidal Crystal Class.
The 4-fold rotation axis generates from this face a type II tetragonal monopyramid (Figure 4). The stereographic projection of it is shown in Figure 14a.
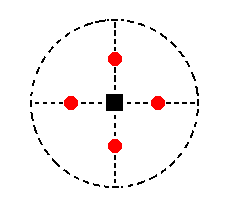
Figure 14a. Stereogram of the hemimorphous Type II Tetragonal Pyramid.
The face a : na : mc is the general face. Its position in the stereogaphic projection is shown in Figure 15.
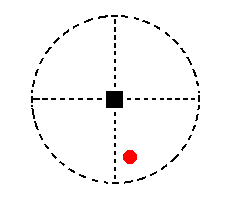
Figure 15. Position of the face a : na : mc in the stereographic projection of the symmetry elements of the Tetragonal-pyramidal Crystal Class.
The 4-fold rotation axis generates a type III tetragonal monopyramid (Figure 6). Its stereographic projection is shown in Figure 15a.
Figure 15a. Stereogram of the hemimorphous Type III Tetragonal Pyramid.
The face a : a : ~c is vertical. Its position is indicated in Figure 16.
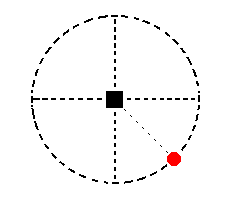
Figure 16. The position of the face a : a : ~c in the stereographic projection of the symmetry elements of the Tetragonal-pyramidal Crystal Class.
The 4-fold rotation axis generates from this face a type I tetragonal prism (Figure 7). Its stereographic projection is indicated in Figure 16a.
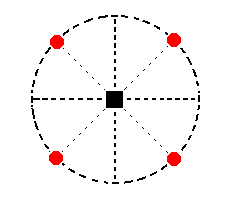
Figure 16a. Stereogram of the hemimorphous Type I Tetragonal Prism.
The face a : ~a : ~c is also vertical. It is moreover parallel to the east-west crystallographic axis. Its position in the stereographic projection is indicated in Figure 17.
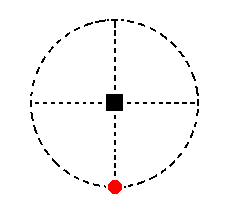
Figure 17. Stereogram of the position of the face a : ~a : ~c in the stereographic projection of the symmetry elements of the Tetragonal-pyramidal Crystal Class.
The 4-fold rotation axis generates from this face the type II tetragonal prism (Figure 8). Its stereographic projection is shown in Figure 17a.
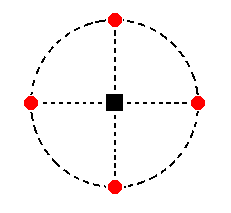
Figure 17a. Stereogram of the hemimorphous Type II Tetragonal Prism.
The face a : na : ~c is also vertical but cuts off a non-unit piece of the east-west crystallographic axis. Its position in the stereographic projection is indicated in Figure 18.
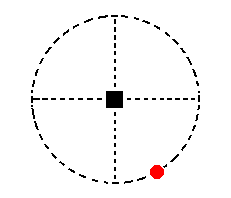
Figure 18. Position of the face a : na : ~c in the stereographic projection of the symmetry elements of the Tetragonal-pyramidal Crystal Class. The 4-fold rotation axis generates from this face a type III tetragonal prism (Figure 9). Its stereographic projection is shown in Figure 18a.
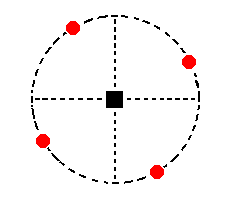
Figure 18a. Stereogram of a hemimorphous Type III Tetragonal Prism.
Recall that the second coefficient (relating to the east-west crystallographic axis) is variable. Its value ranges between n = 1 (type I prism) and n = infinity (type II prism). So the next stereogram is also that of a type III tetragonal prism :
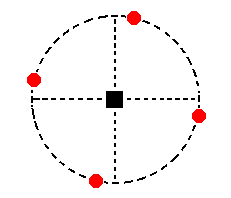
Figure 18b. Stereogram of another Type III hemimorphous Tetragonal Prism.
Finally we have the face ~a : ~a : c. It is horizontally oriented. Its position in the stereographic projection in indicated in Figure 19.
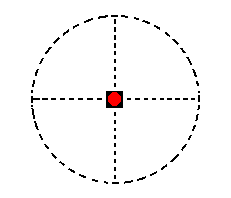
Figure 19. Position of the face ~a : ~a : c in the stereographic projection of the symmetry elements of the Tetragonal-pyramidal Crystal Class.
The only symmetry element of the Class, the 4-fold rotation axis, has no effect on this face, i.e. the face will not be multiplied by this axis. Said differently, when we consider this face to be subjected to the symmetry elements of the present Class, it will be transformed onto itself, by the actions of the 4-fold rotation axis, which actions are : rotations (of the Form) about the main crystallographic axis by 900, 1800, 2700 (and of course, 00 [= 3600] ). So the face ~a : ~a : c turns out to be already a Form all by itself of the present Class. It consists of that one face and is called a pedion (Figure 10a).
Its stereographic projection is of course identical with the one depicted in Figure 19.
This concludes our exposition of the derivation of all the Forms of the Tetragonal-pyramidal Crystal Class, by means of two approaches.
To continue, klick HERE for Part Six.