back to Part One(Alternative name : Quadratic System)
The symmetry content of this Class is :
Protopyramid
Deuteropyramid
Ditetragonal Bipyramid
Protoprism
Deuteroprism
Ditetragonal Prism
Basic Pinacoid
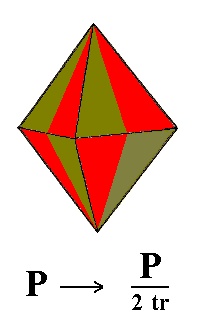
The protopyramid (bipyramid), when subjected to this hemihedric, retains its external shape, but of course looses some symmetry accordingly. We thus obtain a trapezohedric hemihedric type I tetragonal bipyramid. See Figure 1.

Figure 1. The suppression of all the mirror planes of the holohedric Tetragonal Protopyramid (= Type I Bipyramid) yields again a Type I Tetragonal Bipyramid. Concerning the Naumann symbol : By the (sub)symbol "tr" in the expression "2tr" I indicate that we have to do with the trapezohedric hemihedric.
The deuteropyramid (bipyramid), when subjected to this hemihedric, also does not alter its external shape, but looses some symmetry accordingly. We will obtain a trapezohedric hemihedric type II tetragonal bipyramid. See Figure 2.
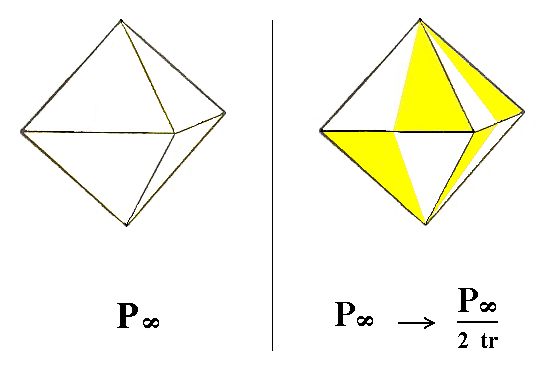
Figure 2. The holohedric Deuteropyramid does not alter its shape when subjected to the trapezohedric hemihedric.
The ditetragonal pyramid (bipyramid) yields two possible tetragonal trapezohedrons, a right one and a left one, as is evident in Figure 3.
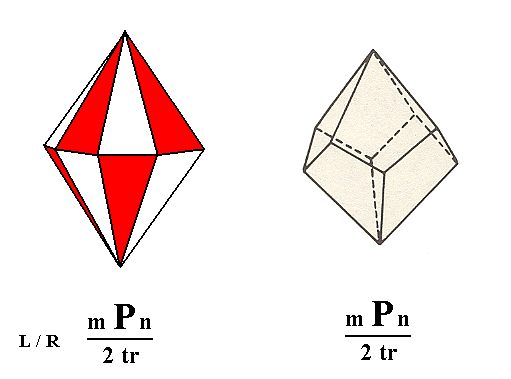
Figure 3. Derivation of a Tetragonal Trapezohedron from a Ditetragonal bipyramid.
Although the scales of the images are slightly different, one can easily see how the Trapezohedron derives from the Ditetragonal Bipyramid by suppressing all mirror planes at once. In the depicted case the Trapezohedron originates from the white faces of the Ditetragonal Bipyramid.
The protoprism does not change its external shape when subjected to this hemihedric, but looses some symmetry accordingly. We obtain a trapezohedric hemihedric type I tetragonal prism, as Figure 4 shows.
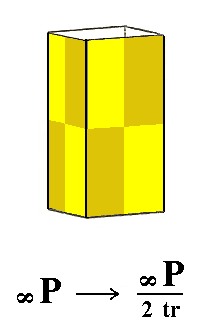
Figure 4. The Protoprism does not change its external shape when subjected to trapezohedric hemihedric.
Also the deuteroprism does not alter its external shape when subjected to this hemihedric. We will obtain a trapezohedric hemihedric Type II tetragonal prism, as Figure 5 shows.
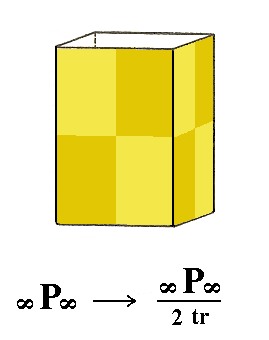
Figure 5. The Deuteroprism retains its shape but looses some symmetry when subjected to trapezohedric hemihedric.
The ditetragonal prism also is not altered with respect to its external shape, when subjected to the trapezohedric hemihedric. We obtain a trapezohedric hemihedric ditetragonal prism. See Figure 6.
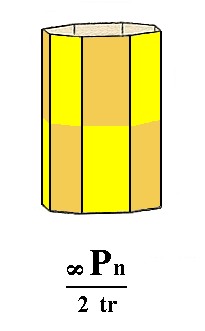
Figure 6. The Ditetragonal Prism retains its external shape when it becomes a trapezohedric hemihedric Ditetragonal Prism.
The basic pinacoid does not alter its external shape (it remains a parallelohedron).
We can explain this as follows (See Figure 7) :
The above Forms of this Class (the tetragonal pyramids and prisms, and the trapezohedron) were merohedrically derived from the holohedric Forms by dropping all the mirror planes. We did this symbolically by alternately coloring the areas lying on either side of a suppressed mirror plane . To make this more explicit we next drop all the faces of one color and let the remaining faces extend till they meet (when their angle is not 1800). In this way we get two possible Forms, one of the one colored set of faces, the other from the other set.
When we adopt the same procedure with respect to the derivation of a trapezohedric hemihedric Form from the holohedric basic pinacoid, we see that, because of this alternating coloring the top face and the bottom face are not symmetrical counterparts anymore. I.e. there is no mirror plane parallel to them (no equatorial mirror plane), because vertically below a yellow area of the top face we find a brown area of the bottom face, and below a brown area of the top face we find a yellow area of the bottom face. Now all the brown faces together form again a basic pinacoid, and the yellow faces together form another pinacoid, but these two pinacoids are exactly identical. So now we can say that the trapezohedric hemihedric generates, from the holohedric basic pinacoid , a trapezohedric hemihedric basic pinacoid.
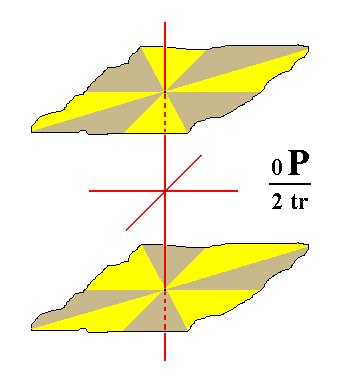
Figure 7. The Basic Pinacoid, when subjected to trapezohedric hemihedric, yields again a Basic Pinacoid, but one with lower symmetry.
All these Forms can engage in combinations.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Tetragonal Crystal System) one by one to the symmetry operations of the present Class (the Tetragonal-trapezohedric Crystal Class).
Recall that the basic faces were the following :
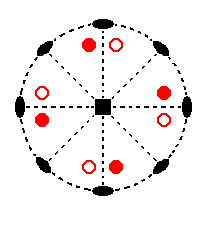
Figure 8. Stereogram of the symmetry elements of the Tetragonal-trapezohedric Crystal Class, and all the faces of the most general Form.
The face a : a : c, the unit face of the Tetragonal Crystal System, cuts off unit pieces from all three crystallographic axes. Its position in the stereographical projection of the symmetry elements of the present Class is shown in Figure 9.
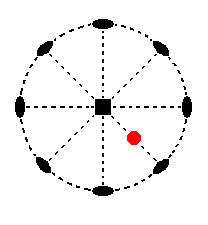
Figure 9. Position of the face a : a : c in the stereographic projection of the symmetry elements of the Tetragonal-trapezohedric Crystal Class.
When we subject this face to the 2-fold rotation axis which goes through it, a second face will be generated exactly below the initial one. When we next apply the 4-fold rotation axis this pair will be multiplied four times resulting in a type I tetragonal bipyramid (Figure 1). The initial face is not allowed to be symmetric because mirror planes are excluded in this Class, So also their multiplication by rotation does not generate any mirror symmetry.
The stereographic projection of the type I tetragonal bipyramid is shown in Figure 9a.
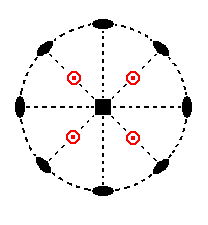
Figure 9a. Stereogram of the trapezohedric hemihedric Type I Tetragonal Bipyramid.
A small red circle, centered with a red point indicates the coinciding projections of a lower face and an upper face (respectively).
The face a : ~a : c is parallel to the east-west crystallographic axis. It cuts off unit pieces from the other two axes. Its position in the stereographic projection in indicated in Figure 10.
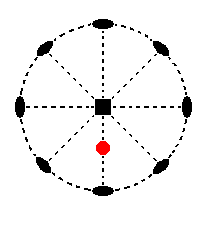
Figure 10. Position of the face a : ~a : c in the stereographic projection of the symmetry elements of the Tetragonal-trapezohedric Crystal Class.
When we subject this face to the 2-fold rotation axis which goes through it, a second face is generated just below the initial one. When we next apply the 4-fold rotation axis this pair will be multiplied four times resulting in a type II tetragonal bipyramid (Figure 2).
Its stereographic projection is shown in Figure 10a.
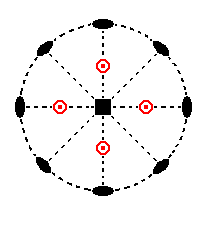
Figure 10a. Stereogram of the trapezohedric hemihedric Type II Tetragonal Bipyramid.
The face a : na : mc is the general face. Its position in the stereographic projection of the symmetry elements of the present Class is shown in Figure 11.
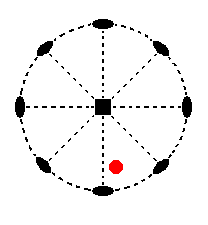
Figure 11. Position of the face a : na : mc in the stereographic projection of the Tetragonal-trapezohedric Crystal Class.
When we subject this face to a nearby 2-fold rotation axis a second face obliquely below it (i.e. not exactly below it) will be generated. When we next subject this pair to the 4-fold rotation axis it will be multiplied four times resulting in a tetragonal trapezohedron (Figure 3).
Its stereographic projection is shown in Figure 11a.

Figure 11a. Stereogram of the Tetragonal Trapezohedron.
The face a : a : ~c is vertical. Its position in the stereographic projection of the symmetry elements of the present Class is indicated in Figure 12.
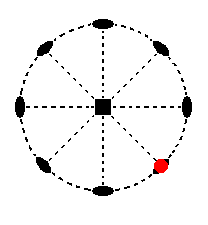
Figure 12. Position of the face a : a : ~c in the stereographic projection of the Tetragonal-trapezohedric Crystal Class.
When we subject this face to the 2-fold rotation axis which goes through it, no second face is generated. The 4-fold rotation axis will multiply the face four times resulting in a type I tetragonal prism (Figure 4). Its stereographic projection is shown in Figure 12a.
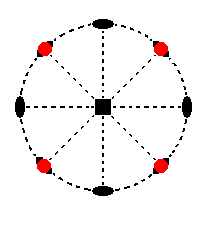
Figure 12a. Stereogram of the trapezohedric hemihedric Type I Tetragonal Prism.
The face a : ~a : ~c is also vertical. It is parallel to the east-west crystallographic axis. Its position in the stereographic projection of the symmetry elements is indicated in Figure 13.
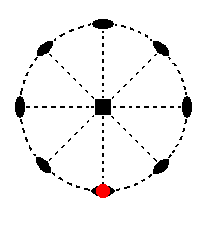
Figure 13. Position of the face a : ~a : ~c in the stereographic projection of the symmetry elements of the Tetragonal-trapezohedric Crystal Class.
Also here the 2-fold rotation axis which goes through this face does not generate a second face. The 4-fold rotation axis multiplies the face four times resulting in a type II tetragonal prism (Figure 5). Its stereographic projection is shown in Figure 13a.
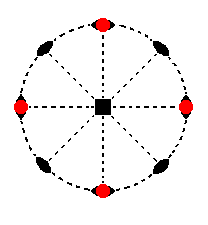
Figure 13a. Stereogram of the trapezohedric hemihedric Type II Tetragonal Prism.
The face a : na : ~c is also vertical, but cuts off a non-unit piece from the east-west crystallographic axis. Its position in the stereographic projection of the symmetry elements of the present Class is indicated in Figure 14.
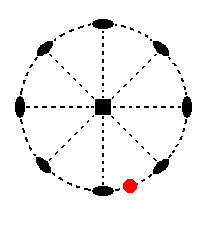
Figure 14. Position of the face a : na : ~c in the stereographic projection of the symmetry elements of the Tetragonal-trapezohedric Crystal Class.
The nearby 2-fold rotation axis will generate a second face that makes an angle (between 00 and 1800) with the initial one. This pair is multiplied four times resulting in a ditetragonal prism (Figure 6). Its stereographic projection is shown in Figure 14a.

Figure 14a. Stereogram of the trapezohedric hemihedric Ditetragonal Prism.
The last face to be considered is the face ~a : ~a : c. It is horizontally orientated. Its position in the stereographic projection of the symmetry elements of the present Class is indicated in Figure 15.
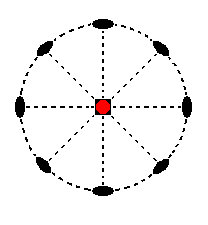
Figure 15. Position of the face ~a : ~a : c in the stereographic projection of the Tetragonal-trapezohedric Crystal Class.
A 2-fold rotation axis will generate a second face parallel to the initial one. The resulting face pair now complies with the other 2-fold axes (they do not have any further effect upon it). The 4-fold rotation axis does not affect this face pair, so the resulting Form is the basic pinacoid (Figure 7). Its stereographic projection is depicted in Figure 15a.
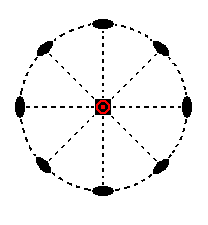
Figure 15a. Stereogram of the trapezohedric hemihedric Basic Pinacoid.
This concludes our exposition of the Tetragonal-trapezohedric Crystal Class.
To continue, klick HERE for Part Seven.