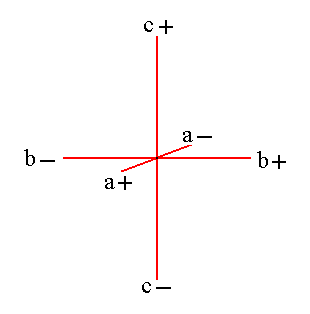
a+ a- is the brachy axis, and b+ b- is the macro axis, while c+ c- is the vertical axis.
(Alternative name : Rhombic System)
The Orthorhombic System contains Forms that can be referred to three non-equivalent (i.e. having unequal lengths) crystallographic axes holding angles of 900 between them. One uses to orient the orthorhombic axial system such that one axis is vertical which is then called the c axis. Whithin this system of crystallographic axes there is no main axis (like there is in the Tetragonal and Hexagonal Systems), which means that any orthorhombic crystal can be orientated arbitrarily. There is indeed no generally accepted convention of how to orient them, i.e. which crystal axis is to be set vertical implying it to be the c axis. In elongated crystals generally the c axis will be chosen along the elongated dimension of such a crystal, while in flattened crystals the c axis will be chosen as perpendicular to the prominent face (which causes the crystal to have a flattened habit).
With respect to the two horizontal crystallographic axes the shorter one is called the brachy axis (= a axis), or brachy diagonal, while the longer one is called the macro axis (= b axis) or macro diagonal. The brachy axis points obliquely to the beholder, while the macro axis is transverse with respect to the beholder.
When the axial ratio is being indicated one sets b = 1, in which b is the macro axis. The other axes are then expressed in terms of b.
Because all the axes are unequal -- and so also the two horizontal axes -- the equatorial plane of the system of orthorhombic crystallographic axes is a rhombus, not a square. A rhombus is a plane figure consisting of four sides of equal length. Two of these sides are parallel to each other, and the other two are also parallel to each other, but not parallel to the former two. Opposite angles are equal, but not 900, and the angles of one set of opposite angles are not equal to those of the other set.
The system of orthorhombic crystallographic axes and its orientation to the beholder is shown in Figure 1, while the equatorial plane of this axial system is shown in Figure 2.
 |
Figure 1. The Orthorhombic System of Crystallographic Axes in its usual orientation. a+ a- is the brachy axis, and b+ b- is the macro axis, while c+ c- is the vertical axis. |
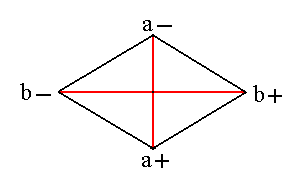 |
Figure 2. The equatorial section of the Orthorhombic System of Crystallographic Axes is a rhombus. a+ a- is the brachy axis, and b+ b- is the macro axis. |
The Forms (A Form is a primary set of faces observing the symmetry of the relevant Crystal Class) are characterized and signified by one of their faces, and such a face in turn is characterized by the proportion of the distances measured from the origin of the axial system to the points of intersection of such a face with those axes (i.e. the proportion of the face's axial cut-off's). In this way we obtain, for Forms of the Orthorhombic System, three derivation coefficients characterizing a face and with it a Form. There are three methods of signifying faces and Forms by means of such derivation coefficients, namely the Weissian (signifying faces or Forms), Naumannian (signifying Forms) and the Millerian (signifying faces or Forms) (See the introductory Essay on The Morphology of Crystals). The Naumann symbols signifying orthorhombic Forms consist of the letter P plus several derivation coefficients. A derivation coefficient in front of (i.e. to the left of) P relates to the c axis cut-off, while a derivation coefficient behind (i.e. to the right of) P either signifies the a axis (= brachy axis) cut-off, or the b axis (= macro axis) cut-off. When a derivation coefficient relates to the (relative cut-off of the) brachy axis a sign
 is placed above the relevant coefficient (to the right of P) or -- as we will do -- above P. When a coefficient relates to the (relative cut-off of the) macro axis a sign
is placed above the relevant coefficient (to the right of P) or -- as we will do -- above P. When a coefficient relates to the (relative cut-off of the) macro axis a sign  is placed above the relevant coefficient, or -- as we will do -- above P.
is placed above the relevant coefficient, or -- as we will do -- above P.
The Hermann-Mauguin symbols signifying the symmetry of each Crystal Class (See also the Essay on The Morphology of Crystals) refer in the following way to the directions relevant in the Orthorhombic Crystal System :
These symbols are written so that the first element refers to the brachy axis (= a axis), the second to the macro axis (= b axis) and the third to the vertical axis (= c axis). In the orthorhombic Crystal Class denoted by the Hermann-Mauguin symbol m m 2, for example, the brachy axis is at right angles to a mirror (m), the macro axis is at right angles to a mirror (m), and the vertical axis is a 2-fold rotation axis (2).
Except for the m m 2 Class where the 2-fold rotation axis is taken as the c axis (vertical axis), no universally accepted convention determines which crystal axis coincides with which symmetry axis (rotation axis).
Derivation of the Forms of each Crystal Class of the Orthorhombic System will go as follows :
We take a face (i.e. an existing well recognizable face of some real orthorhombic crystal) that is supposed to cut each crystallographic axis at its unit distance from the axial origin. Each axis is connected with its own unit distance (which means that the absolute lengths of the three units are not the same). Next we subject this face to the symmetry operations of the highest symmetrical Class of the Orthorhombic system, i.e. we create a set of faces -- one of which is our initial face -- that as a whole, i.e. as a configuration of faces (a Form) complies with the symmetry of the highest symmetrical Class. The symmetry content of this Class consists of
We will now describe in more detail the Basic Form of the Orthorhombic Crystal System, with its Weissian symbol (a : b : c), its Naumann symbol P, and its Miller symbol {111}.
(a refers to the brachy axis, b to the macro axis, and c to the vertical axis).
It is a rhombic bipyramid, implying that its equatorial plane is a rhombus, not a square. This bipyramid consists of eight faces of which each is an unequilateral triangle. It has four equal middle edges and eight polar edges four of which are more obtuse while the other four are more acute. In the conventional orientation two obtuse polar edges, an upper one and a lower one, are directed to the beholder. It has six corners, and every two corners that are opposite to each other are equal. The crystallographic axes pass through the corners.
The symbols for this Basic Form, which is called a primary protopyramid are given above. See Figure 3.
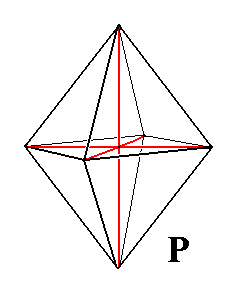 |
Figure 3. The Primary Protopyramid as Basic Form for the Orthorhombic Crystal System. All the Forms of the highest symmetrical Class can be derived from this Basic Form. |
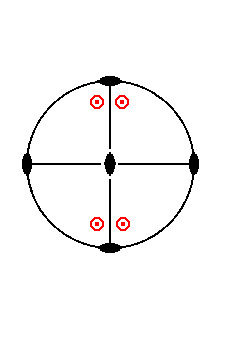 |
Figure 3a. Stereographic projection of the symmetry elements of the Rhombic-bipyramidal Crystal Class, and all the faces of the most general Form, the Rhombic Bipyramid (The position of the faces -- face poles -- is meant to be a general one, as actually depicted it represents a pyramid of the Macrodiagonal Series). Solid ellipses stand for 2-fold rotation axes. The solid circle represents a horizontal mirror plane, while the two straight diagonal lines represent two vertical mirror planes. The small red circles centred with a red dot represent upper and lower faces (face pairs), which -- as face poles -- coincide with each other on the plane of projection, i.e. the projections of the upper and the lower face of such a face pair end up at the same location on the plane of projection. |
Closed Forms (pyramids).
From the above described Basic Form -- the primary (proto-)pyramid -- a number of secondary pyramids can be derived whose axes stand in a rational relationship with those of the primary pyramid. And this does not -- like it does in the Tetragonal and Hexagonal Systems -- concern only one axis, the vertical axis, but all three axes (because there is no main axis to be found in the Orthorhombic Crystal System). This implies that we have three series of derived pyramids :
Varying the relative c axis cut-off distance, which is equivalent to varying the derivation coefficient m in (a : b : mc) and in mP, gives us the Vertical Series, the Protopyramids which can be denoted by the Weissian symbol (a : b : mc), the Naumann symbol mP and the Miller symbol {hhl} :
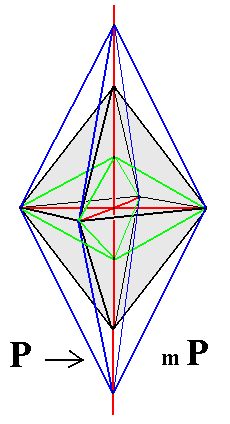 |
Figure 4. From the Primary Pyramid (P) can be derived the Vertical Series, the Protopyramids (mP), by varying the derivation coefficient m. Two possible non-primary (i.e. secondary) Protopyramids are indicated (blue and green respectively). The Primary Pyramid is a Protopyramid in which m = 1. |
Varying the relative a axis cut-off distance, which is equivalent to varying the derivation coefficient n in (na : b : c) and in Pn, gives us the Brachydiagonal Series (Brachypyramids). Because we can derive such brachypyramids from each protopyramid (including the primary protopyramid) the (general) Weissian symbol for a brachypyramid is (na : b : mc), and the corresponding Naumann symbol is
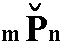 . The Miller symbol is {khl}.
. The Miller symbol is {khl}.
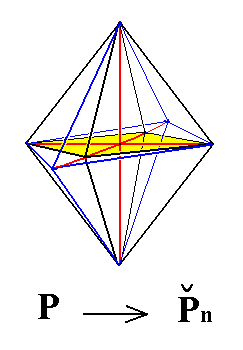 |
Figure 5. From the Primary Pyramid can be derived a Brachy diagonal Series, the primary Brachypyramids, by varying the derivation coefficient n of the Brachy axis. Also from any non-primary Protopyramid (i.e. a non-primary member of the Vertical Series) a Brachypyramid can be derived in the same way, yielding the Brachy diagonal Series. |
Varying the relative b axis cut-off distance, which is equivalent to varying the derivation coefficient n in (a : nb : c) and in Pn, gives us the Macrodiagonal Series (Macropyramids). Because we can derive such macropyramids from each protopyramid (including the primary protopyramid) the (general) Weissian symbol for a macropyramid is (a : nb : mc), and the corresponding Naumann symbol is
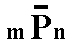 . The Miller symbol is {hkl}.
. The Miller symbol is {hkl}.
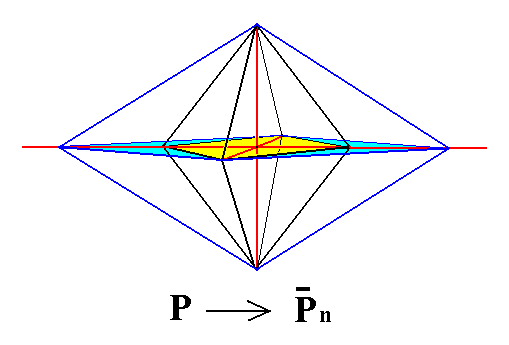
Figure 6. A primary Macropyramid (blue), derived from the primary Protopyramid.
Also from any Protopyramid of the Vertical Series can a Macropyramid be derived, by extention of the macro axis.
Open Forms (vertical and horizontal prisms and pinacoids).
 |
Figure 7. From any Rhombic Protopyramid (a : b : mc) can be derived the Rhombic Protoprism (a : b : ~c) by making m infinitely large. |
From the pyramids of the Brachydiagonal Series (na : b : mc) a second category of vertical prisms, the brachyprisms (na : b : ~c) (Miller symbol {kh0}) can be derived when we again make the derivation coefficient m infinitely large :
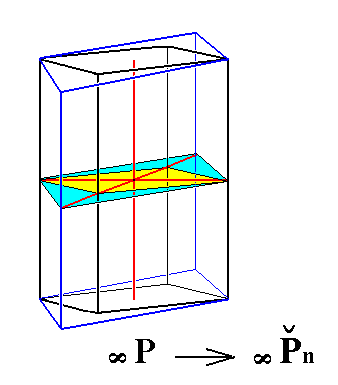 |
Figure 8. From any Rhombic Brachypyramid (na : b : mc) can be derived a Rhombic Brachyprism (na : b : ~c) by making m infinitely large. Here we derive such a Brachyprism directly from the Rhombic Protoprism, by extention of the cut-off distances of the brachy axis. |
Like in the Rhombic Protoprism the horizontal section of the Brachyprisms is a rhombus. See Figure 9.
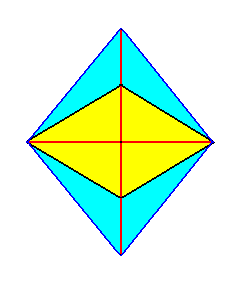 |
Figure 9. Horizontal sections through a Rhombic Protoprism (yellow) and a possible Rhombic Brachyprism (blue). Both are rhombi. |
From the pyramids of the Macrodiagonal Series (a : nb : mc) a third category of vertical prisms, the macroprisms (a : nb : ~c) ({hk0}) can be derived when we again make the derivation coefficient m infinitely large :
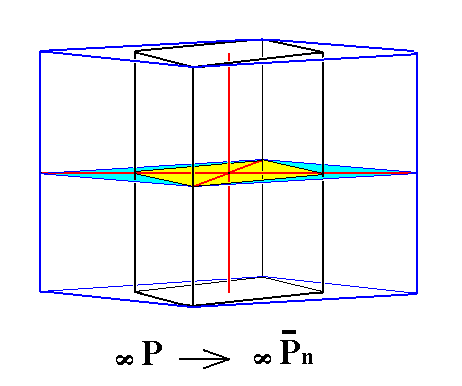
Figure 10. From any Rhombic Macropyramid (a : nb : mc) can be derived a Rhombic Macroprism (a : nb : ~c) by making m infinitely large. Here we derive such a Macroprism directly from the Rhombic Protoprism, by extention of the cut-off distances of the macro axis.
Also the horizontal sections of the macroprisms are rhombi, as the next Figure illustrates :
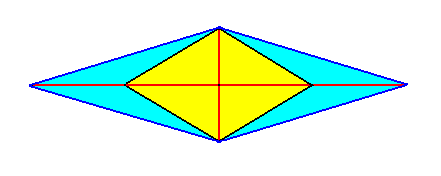
Figure 11. Horizontal sections through the Rhombic Protoprism (yellow) and a possible Macroprism (blue).
Further we can derive two categories of horizontal rhombic prisms that often are also called domes :
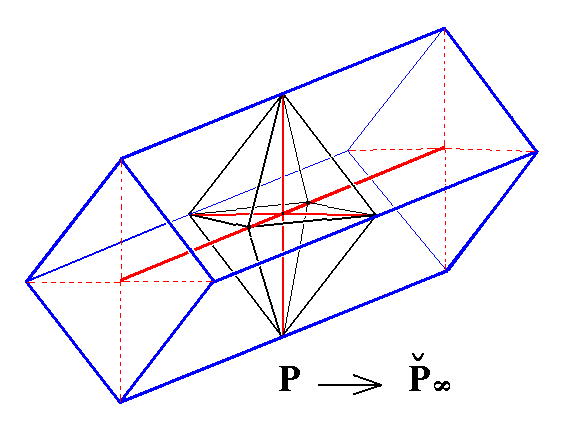
Figure 12. Derivation of the primary Brachydome ( in which m = 1 ) from the primary Protopyramid. It is an open Form (front side and back side open) -- the straight lines bordering its front and rear ends should not suggest a front and back face -- consisting of four faces parallel to the brachy axis. It is a horizontal rhombic prism.
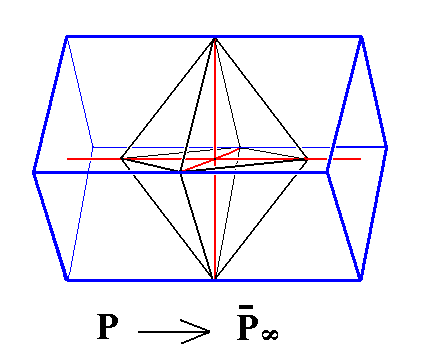
Figure 13. Derivation of the primary Macrodome ( in which m = 1 ) from the primary Protopyramid. It is an open Form (left side and right side open) -- the straight lines bordering its left and right ends should not suggest a left and right face -- consisting of four faces parallel to the macro axis. It is a horizontal rhombic prism.
Finally we can derive three more Forms of this Crystal Class, the pinacoids. They are Forms in which each face intersects only one and the same crystallogaphic axis :
To show the derivation, let us first depict the above constructed (primary) brachydome as it is all by itself. The Figure shows a shortened version of it which is immaterial because the length of the (horizontal) prism is not determined.
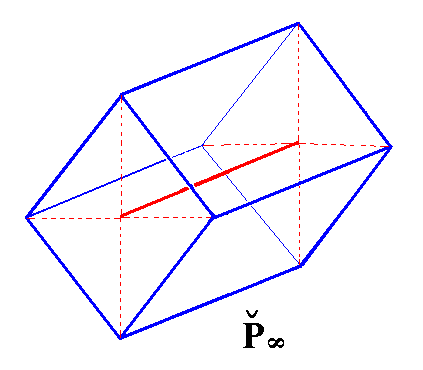 |
Figure 14. The primary Brachydome. The red solid line is the brachy axis. |
From this brachydome we can now derive the brachy pinacoid :
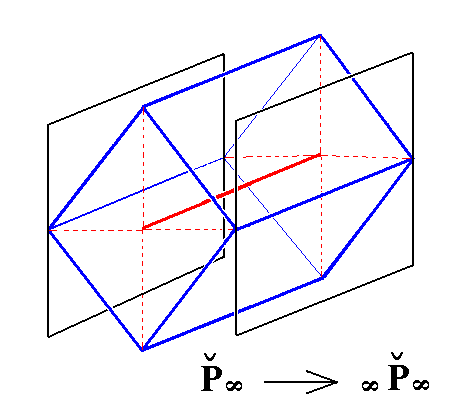 |
Figure 15. Derivation of the Brachy Pinacoid from the primary Brachydome. The red solid line is the brachy axis. |
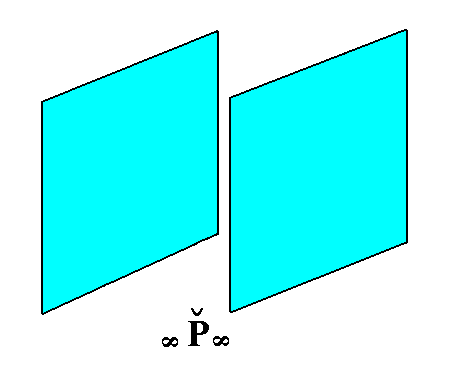 |
Figure 16. The Brachy Pinacoid. This Form consists of two vertical faces parallel to the brachy axis. |
Like the other pinacoids and all the prisms, the brachy pinacoid is an open Form and can only exist in real crystals when combined with Forms of this Crystal Class such that the combination is a closed structure.
From the macrodomes (a :~b : mc) (or from the primary macrodome (a :~b : c), for that matter), we can derive the macro pinacoid (a :~b : ~c) ({100}), by letting m (which is equal to 1 in the primary macrodome) become infinite . It consists of two vertical faces parallel to each other and to the macro axis. See Figure 17, 18 and 19.
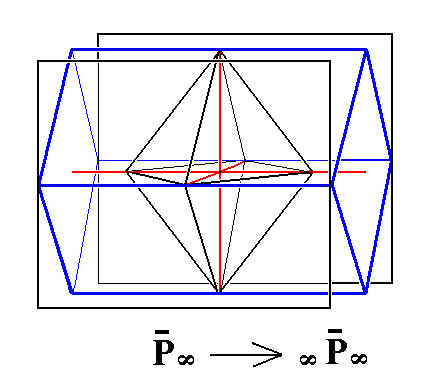 |
Figure 17. Derivation of the Macro Pinacoid from the primary Macrodome. The red lines indicate the crystallographic axes. |
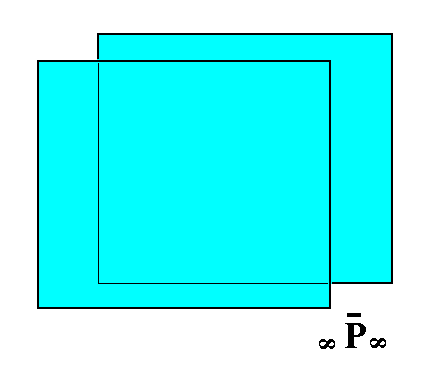 |
Figure 18. The Macro Pinacoid. It consists of two vertical faces parallel to the macro axis. |
Finally the basic pinacoid can be derived from either the brachydome or the macrodome by letting m (which is equal to 1 in the primary domes) become zero. The result will be a horizontal face pair, parallel to the horizontal crystallographic axes (the brachy axis and the macro axis). The Weissian symbol for this Form is (~a : ~b : c).
In the next Figure we will derive the basic pinacoid from the (primary) brachydome :
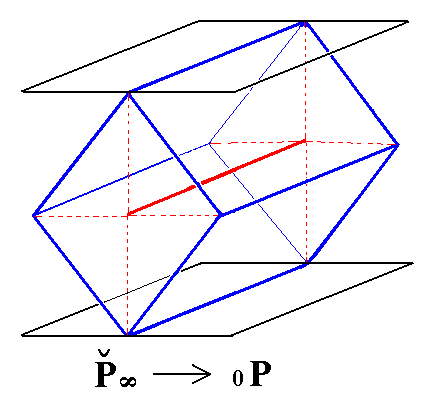 |
Figure 19. Derivation of the Basic Pinacoid from the primary Brachy Dome. |
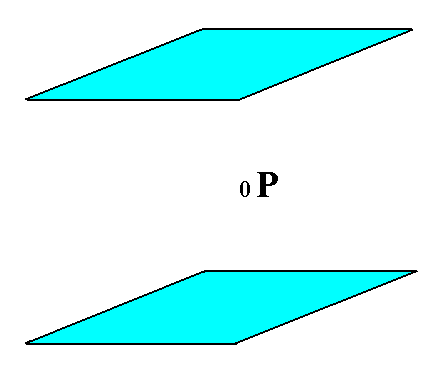 |
Figure 20. The Basic Pinacoid. It consists of two horizontal faces parallel to the brachy and macro axes. |
We now have derived all the Forms of the Rhombic-bipyramidal Crystal Class (= Holohedric Division). These Forms all comply with the symmetry of this Class (2/m 2/m 2/m). And all these Forms can enter in combinations with each other in real Crystals.
The faces that represent each Form are -- with respect to the Weissian symbolism -- placed between brackets (as is done above), for example (~a : ~b : c). As such they are Forms.
These faces themselves -- thus without brackets, i.e. as faces -- are then the eleven Basic Faces compatible with the Orthorhombic Crystal System.
To sum up these basic faces we get :
Subjecting each of these basic faces to the symmetry elements of the present Crystal Class -- which means generating new faces according to the symmetry demands of that Class imposed on the resulting face configuration (Form), i.e. the symmetry that this configuration should have according to those demands -- will yield the above Forms, i.e. the Forms of the Holohedric Division.
Subjecting those same basic faces to the symmetry elements of the other orthorhombic Crystal Classes will result in the Forms of those Classes.
The face a : b : c is the primary face (yielding the primary rhombic protopyramid, (a : b : c), when subjected to the symmetry elements of the present Class). This face, from which all listed faces are derivations, is taken from a conspicuous face of some (real) crystal belonging to the present Crystal Class.
That the above list of basic faces is complete can be shown by the location of their poles in the stereographic projection of the symmetry elements of the present Class :
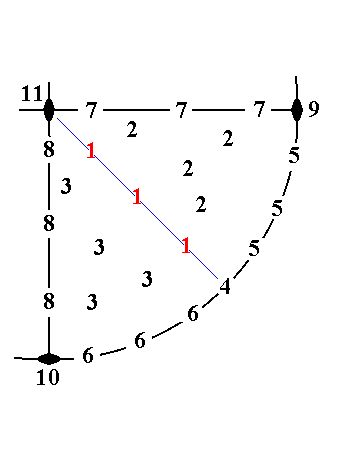 |
Figure 21. The lower right quadrant of the stereographic projection of the symmetry elements of the Rhombic-bipyramidal Class, and the possible locations of faces (face categories).
|
In the above Figure the straight solid black lines are vertical mirror planes, perpendicular to each other. The solid circumference of the the circle (one quarter shown) represents the equatorial mirror plane. The black solid ellipses signify 2-fold rotation axes. Two of them are horizontal and coincide with the two horizontal crystallogaphic axes (the vertically drawn axis is the brachy axis, the horizontally drawn axis is the macro axis). The third 2-fold rotation axis is vertical and coincides with the c axis, it is perpendicular to the plane of the drawing.
1 represents the faces (face category) a : b : mc. They can vary along the line bisecting the quadrant in two equal halves. They all cut off unit distances of the brachy and macro axes, and can vary with respect to the cut-off distance of the c axis. All these distances are given in the form of a ratio of the three axial cut-off distances. If m = 1 then we have the primary basic face, that generates a primary rhombic protopyramid (a bipyramid) when subjected to the symmetry elements of the present Class. Other finite non-zero values of m will yield derived protopyramids.
2 represents the faces (face category) na : b : mc. Such a face can be everywhere inside the upper sector of the quadrant. When subjected to the symmetry elements of the present Class such a face will yield a brachy pyramid.
3 represents the faces (face category) a : nb : mc. Such a face can be everywhere in the lower sector of the quadrant. When subjected to the symmetry elements of the present Class such a face will yield a macro pyramid
4 represents the face (face category) a : b : ~c. It is vertical and cuts off unit distances from the brachy and macro axes. Only one such face is possible. When it is subjected to the symmetry elements of the present Class it will yield a protoprism.
5 represents the faces (face category) na : b : ~c. They are vertical. When such a face is subjected to the symmetry elements of the present Class it will generate a brachy prism. It can vary along the circle segment bordering the upper sector of the quadrant.
6 represents the faces a : nb : ~c. They are also vertical. When such a face is subjected to the symmetry elements of the present Class it will generate a macro prism. It can vary along the circle segment bordering the lower sector of the quadrant.
7 represents the faces ~a : b : mc. They are parallel to the brachy axis. When such a face is subjected to the symmetry elements of the present Class it will generate a brachydome. It can vary along the the horizontal line in the drawing.
8 represents the faces a : ~b : mc. They are parallel to the macro axis. When such a face is subjected to the symmetry elements of the present Class it will generate a macrodome. It can vary along the the vertical line in the drawing.
9 represents the face ~a : b : ~c. It is vertical and parallel to the brachy axis. Only one such face is possible. When this face is subjected to the symmetry elements of the present Class it will generate a brachy pinacoid.
10 represents the face a : ~b : ~c. It is vertical and parallel to the macro axis. Only one such face is possible. When this face is subjected to the symmetry elements of the present Class it will generate a macro pinacoid.
11 represents the face ~a : ~b : c. It is horizontal. Only one such face is possible. When this face is subjected to the symmetry elements of the present Class it will generate a basic pinacoid.
Remark about the stereographic projection of Orthorhombic crystals :
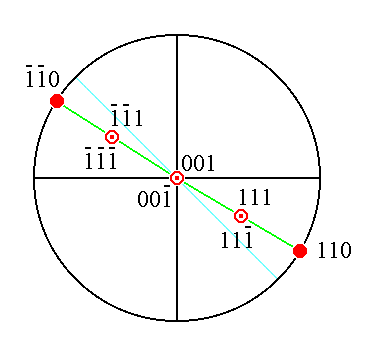
Figure 21a. Stereographic projection of the faces a : b : c (= (111)), a : b : -c (= (111*) (where 1* means a negative Miller index, written as a 1 with a score above it in the literature), -a : -b : c (= (1*1*1)), -a : -b : -c (= (1*1*1*)),
a : b : ~c (= (110)) and -a : -b : ~c (= (1*1*0)) of an orthorhombic crystal.
These faces all have equal derivation coefficients, respectively Miller indices, with a value equal to 1, negative or positive. The absolute cut-off distances are, however, not the same in this case as is to be expected for orthorhombic crystals. So those faces do not lie on the bisector (given in blue) of the relevant quadrants of the projection plane. They do lie, however, on one straight line (given in green), a diameter of the projection plane.
Also the projections of the two horizontal faces ~a : ~b : c (= (001)) and ~a : ~b : -c
(= (001*)) are shown.
In the stereographic projections that follow we will however place the faces with equal derivation coefficients with respect to the brachy axis (= a axis) and macro axis (= b axis) on the bisector of the relevant quadrant of the projection plane (Real crystals actually showing such positions of the relevant faces are not principally excluded in the Orthorhombic System). This we do to let the equality of the derivation coefficients stand out clearly.
Let us now actually execute the above mentioned generations of the Forms when each basic face is subjected to the symmetry elements of the present Class. Of course we'll end up with the same Forms that we have already derived above. But deriving those Forms from the basic faces better shows the fact that the set of derived Forms is complete.
FACIAL APPROACH
The face a : b : mc generates a (derived) protopyramid when subjected to the symmetry elements of the present Class. First the face is duplicated by one vertical mirror plane, then the two faces are again duplicated by the other vertical mirror plane, resulting in four faces, forming a monopyramid. Then this monopyramid is reflected in the horizontal mirror plane resulting in a bipyramid. The rest of the symmetry elements is then implied.
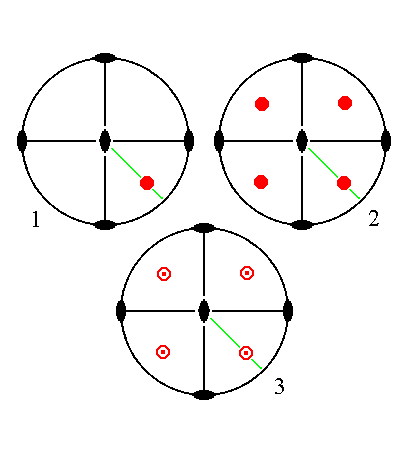 |
Figure 22. (1). Position of the face a : b : mc in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Generation of four faces in virtue of the action of the two vertical mirror planes (straight solid black lines). (3). Reflection of those four faces in the equatorial mirror plane (black solid circle). The small centred red circles indicate a pair of upper and lower faces. |
The face na : b : mc generates a brachy pyramid when subjected to the symmetry elements of the present Class. The face is duplicated by one vertical mirror plane. Then the resulted face pair is duplicated by the other vertical mirror plane. Finally the four resulted faces are reflected in the equatorial mirror plane resulting in a bipyramid. The other symmetry elements are then implied.
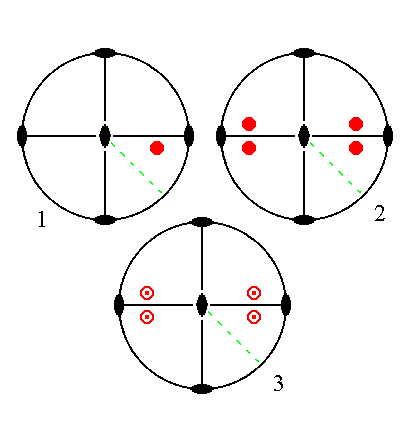 |
Figure 23. (1). Position of the face na : b : mc in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Generation of four faces in virtue of the action of the two vertical mirror planes (straight solid black lines). (3). Reflection of those four faces in the equatorial mirror plane (black solid circle). |
The face a : nb : mc generates a macropyramid when subjected to the symmetry elements of the present Class. It will be duplicated by one vertical mirror plane and again duplicated by the other vertical mirror plane. Then the resulted four faces are reflected in the equatorial mirror plane resulting in a bipyramid. The other symmetry elements are then implied.
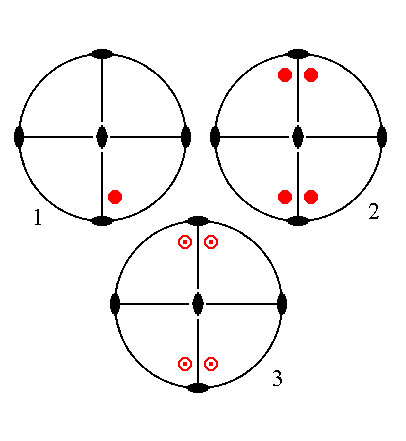 |
Figure 24. (1). Position of the face a : nb : mc in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Generation of four faces in virtue of the action of the two vertical mirror planes (straight solid black lines). (3). Reflection of those four faces in the equatorial mirror plane (black solid circle). |
The face a : b : ~c is vertical. It generates the rhombic protoprism when subjected to the symmetry elements of the present Class : The face is duplicated by one vertical mirror plane, and the resulted face pair is again duplicated (now) by the other vertical mirror plane, resulting in four vertical faces. The other symmetry elements are then implied. See figure 25.
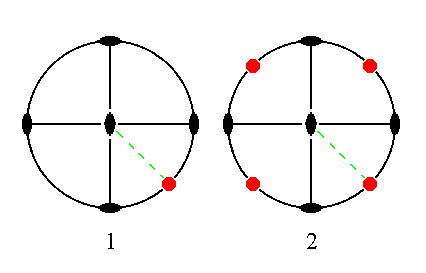 |
Figure 25. (1). Position of the face a : b : ~c in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Generation of four faces in virtue of the action of the two vertical mirror planes, making up a prism. |
The face na : b : ~c is also vertical. It generates a brachyprism when subjected to the symmetry elements of the present Class : The face is duplicated by one vertical mirror plane, and the resulted face pair is again duplicated (now) by the other vertical mirror plane, resulting in four vertical faces making up a prism. See Figure 26.
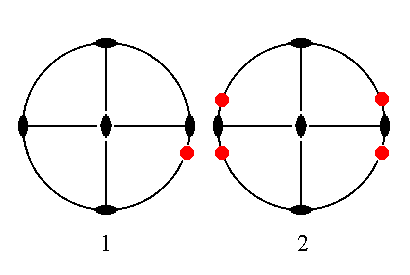 |
Figure 26. (1). Position of the face na : b : ~c in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Generation of four faces in virtue of the action of the two vertical mirror planes, making up a prism. |
The face a : nb : ~c is also vertical. It generates a macroprism when subjected to the symmetry elements of the present Class : The face will be duplicated by one vertical mirror plane and the result is again duplicated (now) by the other vertical mirror plane, resulting in four vertical faces making up a prism. All other symmetries of the Class are then implied.
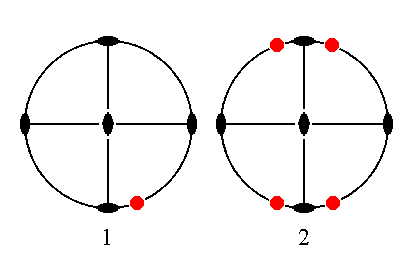 |
Figure 27. (1). Position of the face a : nb : ~c in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Generation of four faces in virtue of the action of the two vertical mirror planes, making up a prism. |
The face ~a : b : mc is parallel to the brachy axis. It generates a brachydome when subjected to the symmetry elements of the present Class : The face is duplicated by the vertical mirror plane in which the brachy axis lies (or, having the same effect in this case, it is duplicated by the vertical 2-fold rotation axis). The resulting face pair is then reflected in the equatorial mirror plane, yielding four faces parallel to the brachy axis making up a horizontal prism, in this case a brachydome. See Figure 28.
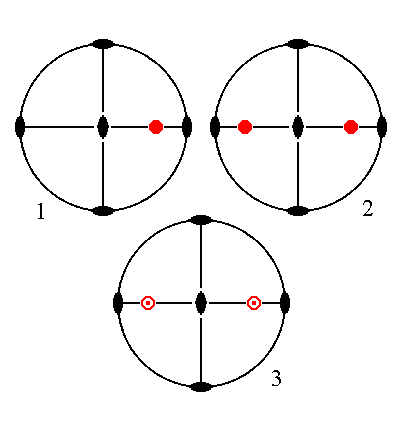 |
Figure 28. (1). Position of the face ~a : b : mc in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Duplication of the face in virtue of the action of the vertical mirror plane in which the brachy axis lies. (3). The resulted face pair is then in turn duplicated by the action of the equatorial mirror plane yielding four faces parallel to the brachy axis, making up a horizontal prism. |
The face a : ~b : mc is parallel to the macro axis. It generates a macrodome when subjected to the symmetry elements of the present Class : The face is duplicated by the action of the vertical mirror plane in which the macro axis lies (or, giving the same result, is duplicated by the action of the vertical 2-fold rotation axis). Then the resulted face pair is reflected in the equatorial mirror plane yielding four faces parallel to the macro axis, a horizontal prism, in the present case a macrodome. See Figure 29.
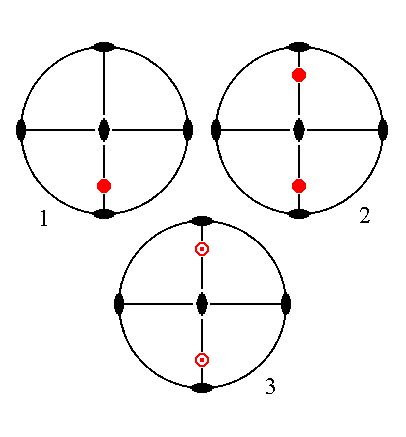 |
Figure 29. (1). Position of the face a : ~b : mc in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Duplication of the face in virtue of the action of the vertical mirror plane in which the macro axis lies. (3). The resulted face pair is then in turn duplicated by the action of the equatorial mirror plane yielding four faces parallel to the macro axis, making up a horizontal prism. |
The face ~a : b : ~c is vertical and parallel to the brachy axis. It will generate a brachy pinacoid when subjected to the symmetry elements of the present Class : The face is duplicated by the vertical mirror plane that contains the brachy axis (or, having the same effect, it is duplicated by the vertical 2-fold rotation axis). All other symmetries are now implied. The result is a Form consisting of two vertical faces parallel to the brachy axis, the brachy pinacoid. See Figure 30.
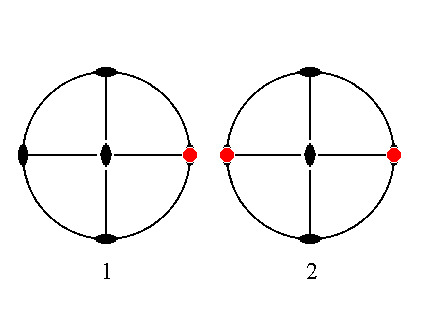 |
Figure 30. (1). Position of the face ~a : b : ~c in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Duplication of the face in virtue of the action of the vertical mirror plane in which the brachy axis lies, resulting in a vertical face pair parallel to the brachy axis. |
The face a : ~b : ~c is vertical and parallel to the macro axis. It generates a macropinacoid when subjected to the symmetry elements of the present class : The face is duplicated by the action of the vertical mirror plane that contains the macro axis (or, giving the same effect, it is duplicated by the action of the vertical 2-fold rotation axis), resulting in a vertical face pair parallel to the macro axis, making up the macro pinacoid. See Figure 31.
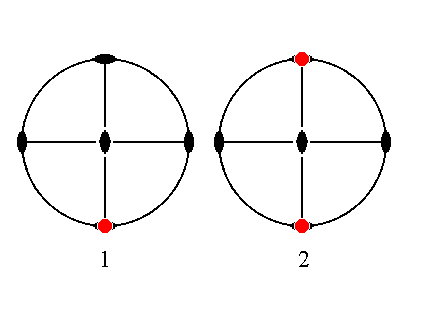 |
Figure 31. (1). Position of the face a : ~b : ~c in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Duplication of the face in virtue of the action of the vertical mirror plane in which the macro axis lies, resulting in a vertical face pair parallel to the macro axis. |
The face ~a : ~b : c, finally, is horizontal. It generates a basic pinacoid when subjected to the symmetry elements of the present Class : The face is reflected in the equatorial mirror plane, resulting in a horizontal face pair, the basic pinacoid. The other symmetries of the Class are then implied. See Figure 32.
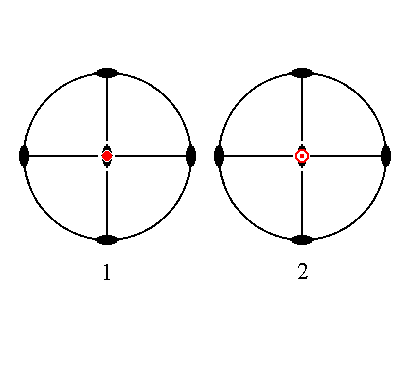 |
Figure 32. (1). Position of the face ~a : ~b : c in the stereogram of the symmetry elements of the Rhombic-bipyramidal Crystal Class. (2). Duplication of the face in virtue of the action of the horizontal mirror plane (that contains the brachy and the macro axis) resulting in a horizontal face pair parallel to the brachy and macro axis. |
This concludes our exposition of the Rhombic-bipyramidal Crystal Class (= Holohedric Division of the Orthorhombic Crystal System).
To continue, klick HERE for Part Two (Class m m 2).