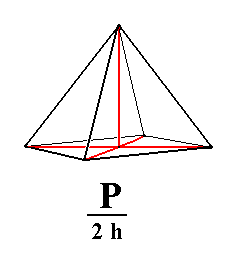
From any Protopyramid (i.e. from any member of the Vertical Series) can be derived the corresponding Rhombic Monopyramid.
The sign "2h" in the Naumann symbol means that hemimorphy is being applied.
(Alternative name : Rhombic System)
The symmetry elements of the present Class, the Rhombic-pyramidal Class (= Hemimorphous Division), are then the following :
The Forms of this Class will be derived from the Holohedric Forms by subjecting them to hemimorphy, which here means that we suppress one mirror plane. As has been said, the 2-fold rotation axis perpendicular to this (now suppressed) mirror plane will be considered to be coincident with the crystallographic c axis which is (by convention) placed vertically.
Recall from Part One that the holohedric Forms of the Orthorhombic System were the following :
Protopyramid
Brachypyramid
Macropyramid
Protoprism
Brachyprism
Macroprism
Brachydome
Macrodome
Brachypinacoid
Macropinacoid
Basic Pinacoid
From the holohedric rhombic protopyramid we can derive two hemimorphous rhombic monopyramids of the Vertical Series, an upper one and a lower one, when hemimorphy is applied to it. The upper monopyramid is depicted in figure 1.
 |
Figure 1. From the holohedric Primary Pyramid can be derived the primary Rhombic Monopyramid, when applying hemimorphy to it. From any Protopyramid (i.e. from any member of the Vertical Series) can be derived the corresponding Rhombic Monopyramid. The sign "2h" in the Naumann symbol means that hemimorphy is being applied. |
From the holohedric rhombic brachypyramid can be derived two hemimorphous rhombic monopyramids of the Brachydiagonal Series, when hemimorphy is applied to it. See Figure 2.
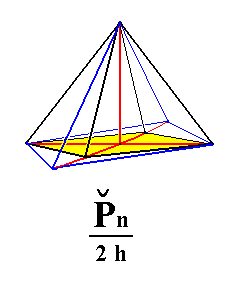 |
Figure 2. From a holohedric Primary Brachy Pyramid can be derived a primary Rhombic Monopyramid (from the Brachydiagonal Series), when applying hemimorphy to it. From any Brachypyramid (i.e. from any member of the Brachydiagonal Series) can be derived the corresponding Rhombic Monopyramid. The sign "2h" in the Naumann symbol means that hemimorphy is being applied. |
From the holohedric rhombic macropyramid can be derived two hemimorphous rhombic monopyramids of the Macrodiagonal Series, when hemimorphy is applied to it. See Figure 3.
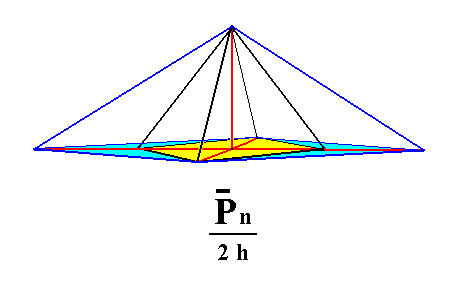
Figure 3. From a holohedric Primary Macropyramid can be derived a primary Rhombic Monopyramid (from the Macrodiagonal Series), when applying hemimorphy to it.
From any Macropyramid (i.e. from any member of the Macrodiagonal Series) can be derived the corresponding Rhombic Monopyramid.
The sign "2h" in the Naumann symbol means that hemimorphy is being applied.
From the holohedric rhombic protoprism can be derived the hemimorphous rhombic protoprism when applying hemimorphy. There is no change in external shape involved, but the symmetry content is lowered accordingly. See Figure 4.
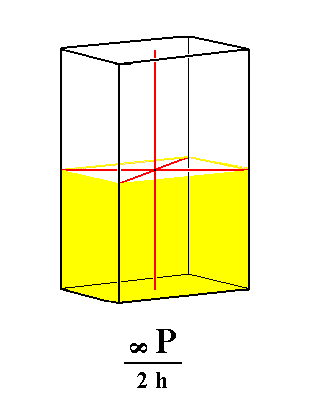 |
Figure 4. From the holohedric Protoprism can be derived the hemimorphous Protoprism, when applying hemimorphy to it. The external shape remains the same. |
From the holohedric rhombic brachyprism can be derived the hemimorphous rhombic brachyprism when hemimorphy is applied to it. The external shape is unaffected.
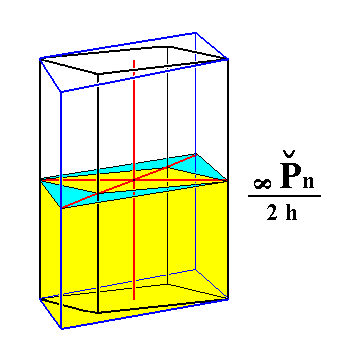 |
Figure 5. From the holohedric Brachyprism can be derived the hemimorphous Brachyprism, when applying hemimorphy to it. The external shape remains the same. |
From the holohedric rhombic macroprism can be derived the hemimorphous rhombic macroprism when hemimorphy is applied to it. The external shape is unaffected.
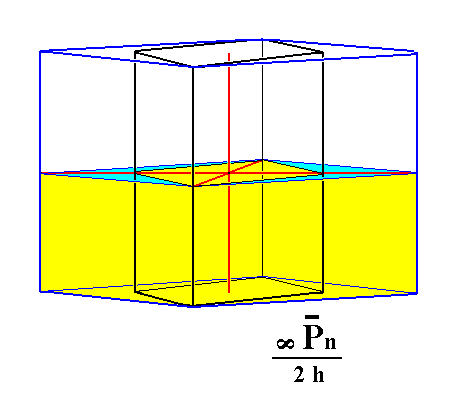 |
Figure 6. From the holohedric Macroprism can be derived the hemimorphous Macroprism, when applying hemimorphy to it. The external shape remains the same. |
From the holohedric rhombic brachydome can be derived two hemimorphous hemidomes, in this case hemibrachydomes, when hemimorphy is applied to it : The brachydome decays into two independent halves, an upper and a lower one. See Figure 7.
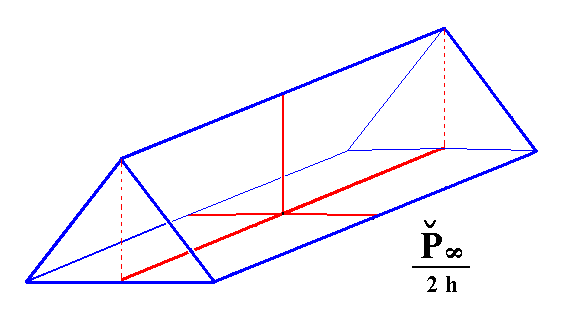
Figure 7. From the primary Brachydome is derived the primary hemimorphous (upper) Hemibrachydome.
From any Brachydome (i.e. not only from the primary one) corresponding hemimorphous Hemidomes can be derived.
Like the vertical prisms these Hemidomes are open Forms. The straight lines bordering the lower end of the upper Hemidome should not suggest the presence of a horizontal face : A Hemidome is a Form consisting of only two faces.
From the holohedric rhombic macrodome can be derived two hemimorphous Hemimacrodomes, when hemimorphy is applied to it : The macrodome decays into two independent halves, an upper and a lower one. See Figure 8.
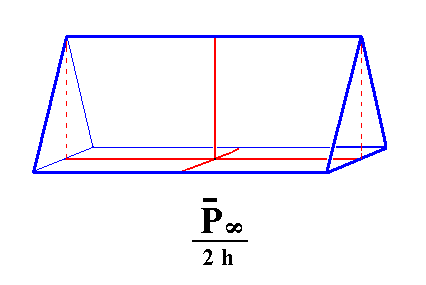
Figure 8. From the primary Macrodome is derived the primary hemimorphous (upper) Hemimacrodome.
From any Macrodome (i.e. not only from the primary one) corresponding hemimorphous Hemidomes can be derived.
Like the vertical prisms these Hemidomes are open Forms. The straight lines bordering the lower end of the upper Hemidome should not suggest the presence of a horizontal face : A Hemidome is a Form consisting of only two faces.
From the holohedric brachy pinacoid we can derive the hemimorphous brachy pinacoid, when hemimorphy is applied to it. Like the vertical prisms, it does not change its external shape. See Figure 9.
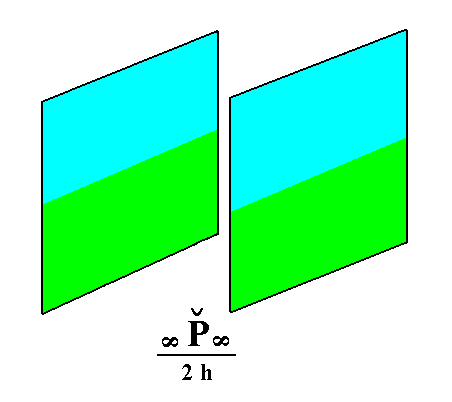 |
Figure 9. From the holohedric Brachy Pinacoid can be derived the hemimorphous Brachy Pinacoid, when applying hemimorphy to it. The external shape remains the same. |
From the holohedric macro pinacoid can be derived the hemimorphous macro pinacoid when hemimorphy is applied to it. The external shape remains the same. See Figure 10.
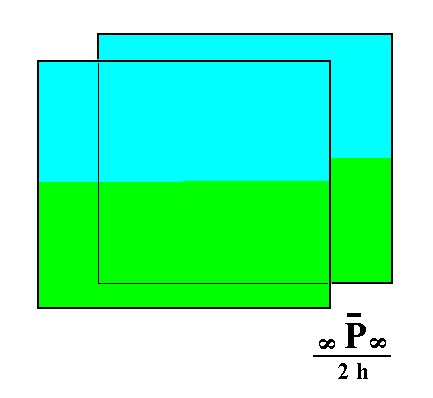 |
Figure 10. From the holohedric Macro Pinacoid can be derived the hemimorphous Macro Pinacoid, when applying hemimorphy to it. The external shape remains the same. |
From the holohedric basic pinacoid can be derived two pedions, that are single faces (monohedra), an upper one and a lower one, when hemimorphy is applied to it. So here we have a Form consisting of just one face. See Figure 11.
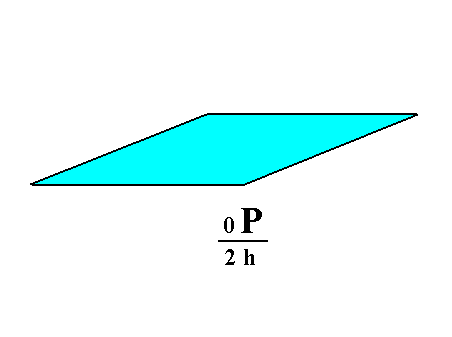 |
Figure 11. From the holohedric Basic Pinacoid (which itself consists of two horizontal faces) can be derived the hemimorphous Pedion (Monohedron), when applying hemimorphy to it. This Pedion is an open Form, it is just one horizontal face. |
This concludes our derivation of all the Forms of the Rhombic-pyramidal Crystal Class, by the merohedric approach.
All these Forms can enter in combinations with each other in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Orthorhombic Crystal System) one by one to the symmetry operations of the present Class (the Rhombic-pyramidal Crystal Class).
In Part One we found the following eleven basic faces compatible with the Orthorhombic Crystal System :
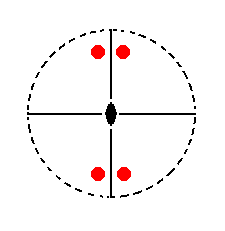 |
Figure 12. Stereogram of the symmetry elements of the Rhombic-pyramidal Crystal Class, and of all the faces of the most general Form. There are two mirror planes, perpendicular to each other, indicated by straight solid lines, each containing one of the two horizontal crystallographic axes. Further there is one vertical 2-fold rotation axis (indicated by a small solid ellips). There is no horizontal (i.e. perpendicular to the 2-fold rotation axis) mirror plane, indicated by the dashing of the circumference of the projection plane. |
The face a : b : mc generates the upper half of a rhombic protopyramid, a rhombic monopyramid of the Vertical Series, when subjected to the symmetry elements of the present Class : The face is duplicated by one of the two mirror planes, and the resulting face pair is again duplicated, yielding four faces that make up a monopyramid. The 2-fold rotation axis is then implied. See Figure 13 and 13a.
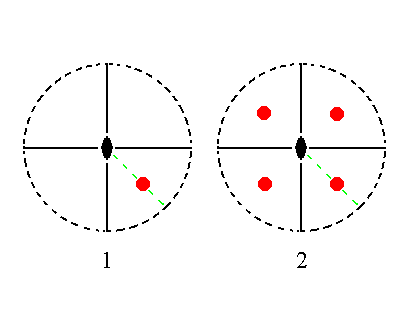 |
Figure 13. (1). Position of the face a : b : mc in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in one of the two mirror planes giving two faces, and these are in turn reflected in the other mirror plane resulting in four faces making up a monopyramid. |
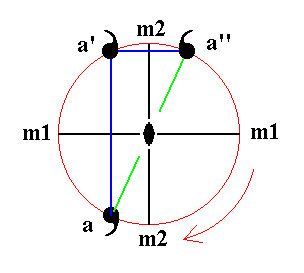
Figure 13a. In this Figure it is explained why the 2-fold rotation axis is implied by the other symmetry elements.
We have drawn two vertical mirror planes, m1 and m2, perpendicular to each other. Their line of intersection coincides (in our drawing) with a vertical 2-fold rotation axis (perpendicular to the plane of the drawing).
When motif a, in the form of a comma, is relected in m1 the image a' is generated. When this newly generated motif is reflected in m2 a motif a" is generated.
But when we take motif a and subject it to the action of the 2-fold rotation axis (a rotation about this axis by 1800) we directly obtain motif a". So we see that this 2-fold rotation axis is already implied by the presence of the two mirror planes.
The face na : b : mc generates the upper half of a rhombic brachypyramid, i.e. a monopyramid of the Brachydiagonal Series, when subjected to the symmetry elements of the present Class : The face is duplicated by one of the mirror planes yielding two faces. This face pair is then duplicated by the other mirror plane resulting in four faces making up a monopyramid. The 2-fold rotation axis is then implied. See Figure 14.
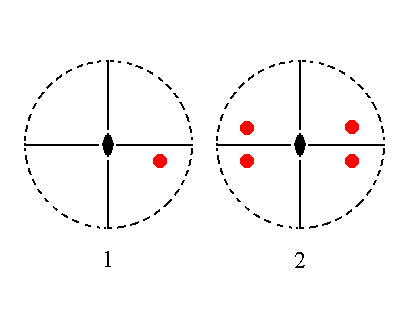 |
Figure 14. (1). Position of the face na : b : mc in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in one of the two mirror planes giving two faces, and these are in turn reflected in the other mirror plane resulting in four faces making up a monopyramid. |
The face a : nb : mc will generate the upper half of a rhombic macropyramid, i.e. a monopyramid of the Macrodiagonal Series, when subjected to the symmetry elements of the present Class : The face will be duplicated by one of the two mirror planes yielding a face pair, which is in turn duplicated by the other mirror plane resulting in four faces making up a monopyramid. The 2-fold rotation axis is then implied. See Figure 15.
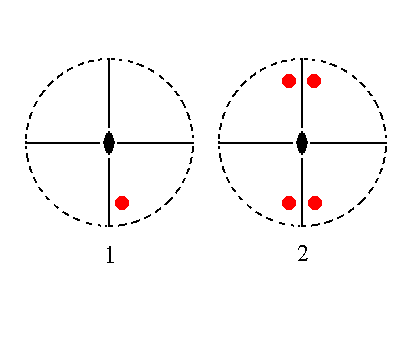 |
Figure 15. (1). Position of the face a : nb : mc in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in one of the two mirror planes giving two faces, and these are in turn reflected in the other mirror plane resulting in four faces making up a monopyramid. |
The face a : b : ~c is vertical. It generates the hemimorphous rhombic protoprism when subjected to the symmetry elements of the present Class : The face is duplicated by one of the mirror planes, and the resulting face pair is in turn duplicated by the other mirror plane, giving a Form consisting of four vertical faces, the rhombic protoprism. The 2-fold rotation axis is implied. See Figure 16.
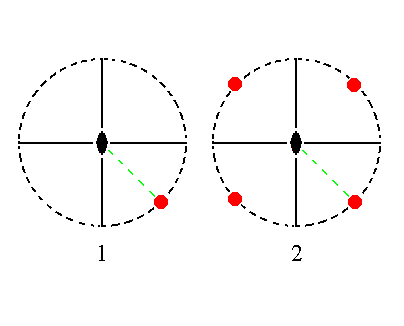 |
Figure 16. (1). Position of the face a : b : ~c in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in one of the two mirror planes giving two faces, and these are in turn reflected in the other mirror plane resulting in four faces making up a prism. |
The face na : b : ~c is also vertical. It generates a hemimorphous brachyprism when subjected to the symmetry elements of the present Class : The face is duplicated by a mirror plane, and the resulting face pair is in turn duplicated by the other mirror plane yielding four vertical faces making up a brachyprism. The 2-fold rotation axis is then implied. See Figure 17.
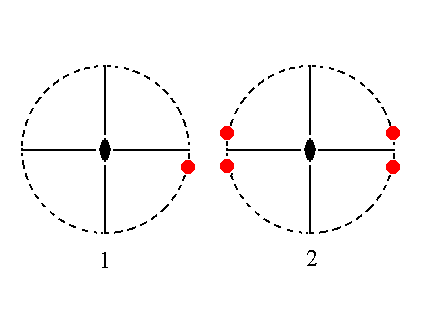 |
Figure 17. (1). Position of the face na : b : ~c in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in one of the two mirror planes giving two faces, and these are in turn reflected in the other mirror plane resulting in four faces making up a prism. |
The face a : nb : ~c is also vertical. It generates a hemimorphous macroprism when subjected to the symmetry elements of the present Class : The face is duplicated by a mirror plane, giving two faces that are in turn duplicated by the other mirror plane resulting in four vertical faces making up a prism. The 2-fold rotation axis is then implied. See Figure 18.
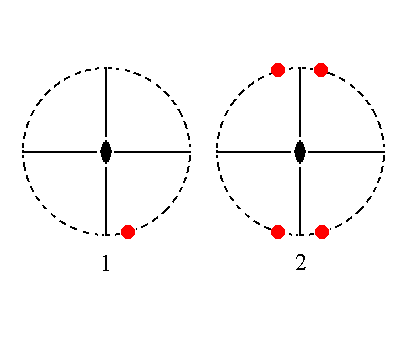 |
Figure 18. (1). Position of the face a : nb : ~c in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in one of the two mirror planes giving two faces, and these are in turn reflected in the other mirror plane resulting in four faces making up a prism. |
The face ~a : b : mc is parallel to the brachy axis and generates the upper half of a brachydome (a hemidome), when subjected to the symmetry elements of the present Class : The face is duplicated by the mirror plane which is not perpendicular to it. The result is a face pair parallel to the brachy axis. The other symmetry elements are implied : The 2-fold rotation axis does not generate new faces (i.e. the face pair has already this 2-fold symmetry). Also the second mirror plane, parallel to the macro axis, does not generate new faces because it is perpendicular to both faces of the generated pair. The latter is, as has been said, a hemidome. See Figure 19.
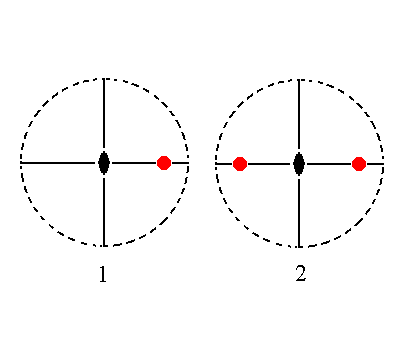 |
Figure 19. (1). Position of the face ~a : b : mc in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in the mirror plane that is not perpendicular to it, and the other symmetry elements do not have any further effect. The result is a pair of faces parallel to the brachy axis, a hemidome. |
The face a : ~b : mc is parallel to the macro axis. It generates the upper half of a macrodome (a hemidome) when subjected to the symmetry elements of the present Class : The face is duplicated by the mirror plane which is not perpendicular to it. The result is a face pair parallel to the macro axis, making up a hemidome. The other symmetry elements are then implied.
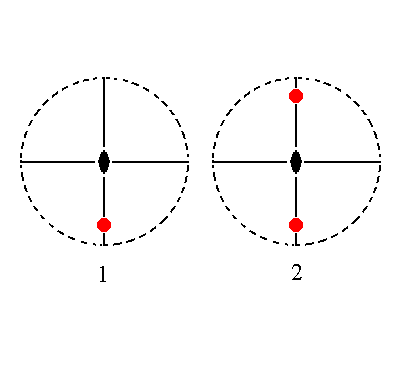 |
Figure 20. (1). Position of the face a : ~b : mc in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in the mirror plane that is not perpendicular to it, and the other symmetry elements do not have any further effect. The result is a pair of faces parallel to the macro axis, a hemidome. |
The face ~a : b : ~c is parallel to the brachy and vertical axes. It generates a hemimorphous brachy pinacoid when subjected to the symmetry elements of the present Class : The face is duplicated by the mirror plane which is not perpendicular to it. The other symmetry elements are then implied. So the result is two vertical faces parallel to the brachy axis. See Figure 21.
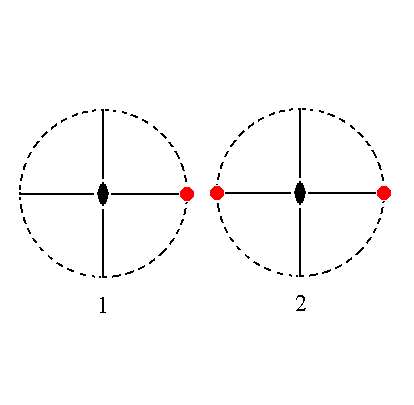 |
Figure 21. (1). Position of the face ~a : b : ~c in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in the mirror plane that is not perpendicular to it, and the other symmetry elements do not have any further effect. The result is a pair of vertical faces parallel to the brachy axis, the Brachy Pinacoid. |
The face a : ~b : ~c is parallel to the macro and vertical axes. It generates a hemimorphous macro pinacoid when subjected to the symmetry elements of the present Class : The face is duplicated by the mirror plane which is not perpendicular to it, resulting in a vertical face pair parallel to the macro axis. The other symmetry elements are then implied. See Figure 22.
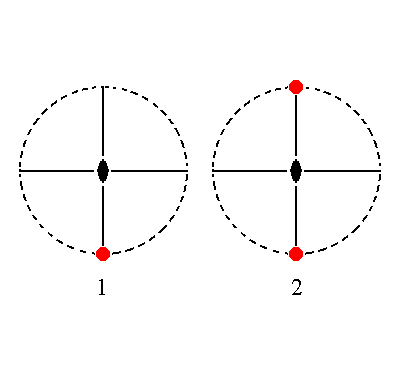 |
Figure 22. (1). Position of the face a : ~b : ~c in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. (2). The face is reflected in the mirror plane that is not perpendicular to it, and the other symmetry elements do not have any further effect. The result is a pair of vertical faces parallel to the macro axis, the Macro Pinacoid. |
The face ~a : ~b : c, finally, is parallel to the brachy and macro axes, i.e. it is horizontal. It generates a pedion, i.e. a single face, when subjected to the symmetry elements of the present Class : Not any one of the symmetry elements does have an effect in the sense that new faces are generated, so we end up with that same single horizontal face, a pedion. See Figure 23.
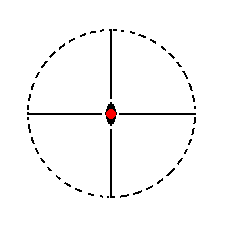 |
Figure 23. Position of the face ~a : ~b : c in the stereographic projection of the symmetry elements of the Rhombic-pyramidal Crystal Class. The actions of all these symmetry elements do not generate new faces, so the resulting Form is just that one horizontal face. |
This concludes our exposition of the Rhombic-pyramidal Crystal Class.
To continue, klick HERE for Part Three (Class 2 2 2).