(Alternative name : Rhombic System)
The symmetry elements of the present Class, the Rhombic-bisphenoidic Class (= Hemihedric Division), are accordingly the following :
The Forms of this Class will be derived from the Holohedric Forms by subjecting them to hemihedric, which here means that we suppress the mirror planes.
Recall from Part One that the holohedric Forms of the Orthorhombic System were the following :
Protopyramid
Brachypyramid
Macropyramid
Protoprism
Brachyprism
Macroprism
Brachydome
Macrodome
Brachypinacoid
Macropinacoid
Basic Pinacoid
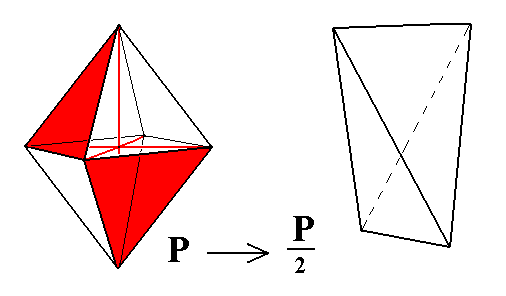
From the holohedric rhombic protopyramid we can derive two rhombic sphenoids(also called bisphenoids) of the Vertical Series. The rhombic sphenoid looks like the tetragonal sphenoid (See Figure 1 of Part Three of the Tetragonal System), but differs from it by the fact that its faces are unequilateral triangles, that the horizontal polar edges (i.e. its upper and lower edges) do not make a right, but an oblique angle with each other, and that the middle edges are alternately equal. See Figure 1.

Figure 1. From the holohedric Primary Pyramid can be derived a primary Rhombic Sphenoid, when applying hemihedric to it. The partition of the pyramid into red and white faces (only shown with respect to the actually visible faces) expresses the suppression of all the mirror planes. Here a Sphenoid is derived from the white faces of the pyramid.
From any Protopyramid (i.e. from any member of the Vertical Series) can be derived the corresponding Rhombic Sphenoid.
The sign "2" in the Naumann symbol means that hemihedric is being applied.
In the same way we can derive the corresponding rhombic sphenoids from the holohedric brachy and macropyramids.
All the remaining holohedric Forms remain externally unchanged when hemihedric is applied to them :
From the holohedric rhombic protoprism can be derived the hemihedric rhombic protoprism when hemihedric is applied to it. The external shape remains the same.
See Figure 2.
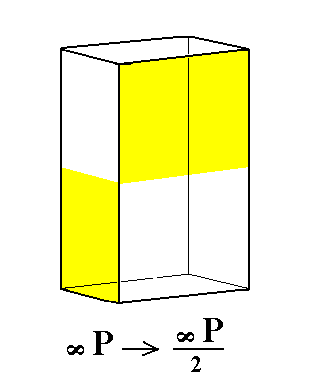 |
Figure 2. From the holohedric Rhombic Protoprism can be derived the hemihedric Rhombic Protoprism, when applying hemihedric to it. As can be seen by the partition of the prism into colored areas (shown only with respect to the actually visible faces), expressing the suppression of all the mirror planes, the external shape remains the same. The sign "2" in the Naumann symbol means that hemihedric is being applied. |
In the same way hemihedric rhombic prisms can be derived from the holohedric brachy and macroprisms.
From the holohedric brachydome can be derived the hemihedric brachydome when hemihedric is applied to it. The external shape remains the same. See figure 3.
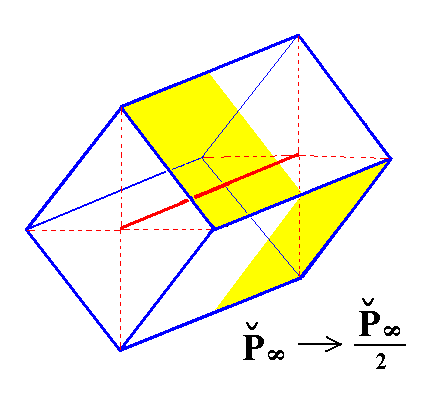 |
Figure 3. From the holohedric Brachydome can be derived the hemihedric Brachydome, when applying hemihedric to it. As can be seen by the partition of the dome into colored areas, expressing the suppression of all the mirror planes, the external shape remains the same. The sign "2" in the Naumann symbol means that hemihedric is being applied. |
From the holohedric macrodome can be derived the the hemihedric macrodome when hemihedric is being applied to it. The external shape remains the same. See Figure 4.
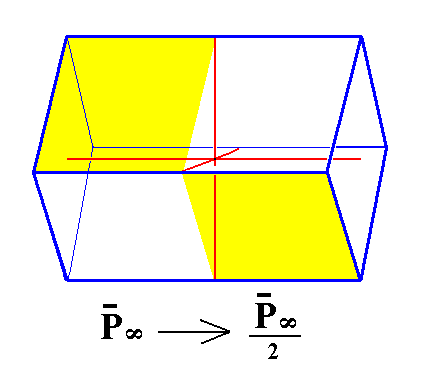 |
Figure 4. From the holohedric Macrodome can be derived the hemihedric Macrodome, when applying hemihedric to it. As can be seen by the partition of the dome into colored areas, expressing the suppression of all the mirror planes, the external shape remains the same. |
From the holohedric brachy pinacoid can be derived the hemihedric brachy pinacoid when hemihedric is applied to it. The external shape remains the same. See Figure 5.
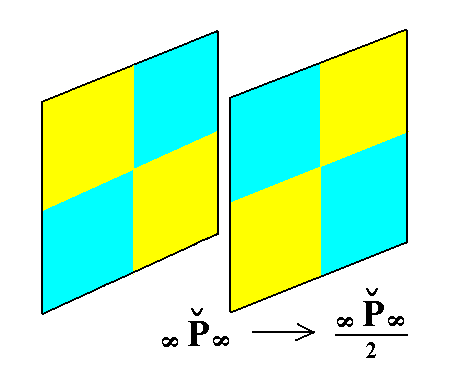 |
Figure 5. From the holohedric Brachy Pinacoid can be derived the hemihedric Brachy Pinacoid, when applying hemihedric to it. As can be seen by the partition of the pinacoid into colored areas, expressing the suppression of all the mirror planes, the external shape remains the same. |
From the holohedric macro pinacoid can be derived the hemihedric macro pinacoid when hemihedric is applied to it. The external shape remains the same. See Figure 6.
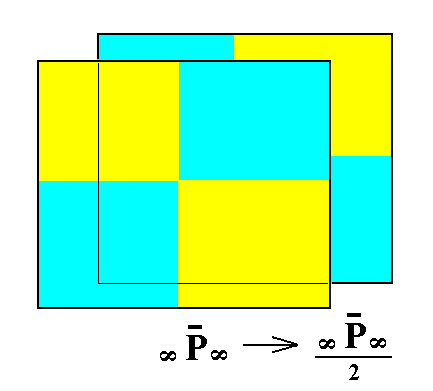 |
Figure 6. From the holohedric Macro Pinacoid can be derived the hemihedric Macro Pinacoid, when applying hemihedric to it. As can be seen by the partition of the pinacoid into colored areas, expressing the suppression of all the mirror planes, the external shape remains the same. |
From the holohedric basic pinacoid can be derived the hemihedric basic pinacoid when hemihedric is applied to it. Its external shape remains the same. See Figure 7.
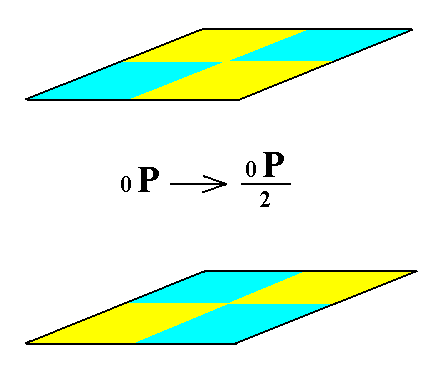 |
Figure 7. From the holohedric Basic Pinacoid can be derived the hemihedric Basic Pinacoid, when applying hemihedric to it. As can be seen by the partition of the pinacoid into colored areas, expressing the suppression of all the mirror planes, the external shape remains the same. |
This concludes our derivation of all the Forms of the Rhombic-bisphenoidic Crystal Class by means of the merohedric approach.
All these Forms can enter in combinations with each other in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Orthorhombic Crystal System) one by one to the symmetry operations of the present Class (the Rhombic-bisphenoidic Crystal Class).
In Part One we found the following eleven basic faces compatible with the Orthorhombic Crystal System :
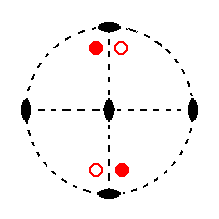 |
Figure 8. Stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class, and of all the faces of the most general Form. There are no mirror planes. The three 2-fold rotation axes are indicated by small black solid ellipses. These rotation axes are perpendicular to each other and coincident with the three crystallographic axes. |
The face a : b : mc generates a rhombic sphenoid when subjected to the symmetry elements of the present Class : First the face is duplicated by the vertical 2-fold rotation axis, resulting in two upper faces. Then one of the two horizontal 2-fold rotation axes generates for each face a corresponding lower face. The result is a Form consisting of four faces, two upper and two lower ones, a sphenoid (also called bisphenoid). The other horizontal 2-fold rotation axis is now implied, as can be seen in the next Figure.
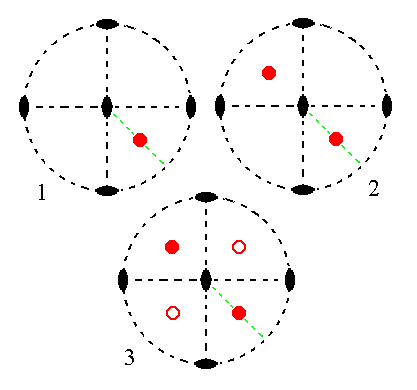
Figure 9.
(1). Position of the face a : b : mc in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face (this is equivalent to demanding that the resulting face configuration -- here the two faces -- has a 2-fold rotational symmetry). Both faces are upper faces.
(3). One of the two horizontal 2-fold rotation axes generates for each face an additional corresponding lower one (indicated by a small open red circle). The final result then also already complies with the other horizontal 2-fold rotation axis, so the resulting face configuration (four faces) has 2 2 2 symmetry (i.e. the symmetry of our Class). It is a Rhombic Sphenoid.
The face na : b : mc generates a rhombic sphenoid when subjected to the symmetry elements of the present Class : The face is duplicated by the vertical 2-fold rotation axis giving two upper faces. These faces get their respective lower faces by the action of a horizontal 2-fold rotation axis, resulting in four faces making up a Rhombic Sphenoid. The other 2-fold rotation axis is then implied. See Figure 10.
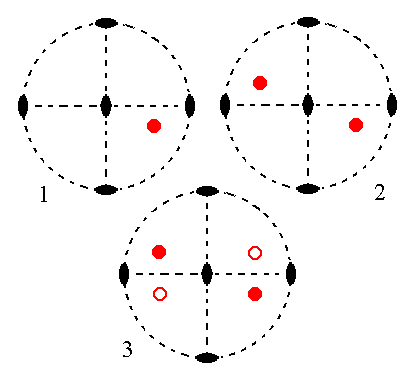
Figure 10.
(1). Position of the face na : b : mc in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face (this is equivalent to demanding that the resulting face configuration -- here the two faces -- has a 2-fold rotational symmetry). Both faces are upper faces.
(3). One of the two horizontal 2-fold rotation axes generates for each face an additional corresponding lower one (indicated by a small open red circle). The final result then also already complies with the other horizontal 2-fold rotation axis, so the resulting face configuration (four faces) has 2 2 2 symmetry (i.e. the symmetry of our Class). It is a Rhombic Sphenoid.
The face a : nb : mc behaves in the same way as the ones above. It generates a rhombic sphenoid when subjected to the symmetry elements of the present Class. See Figure 11.
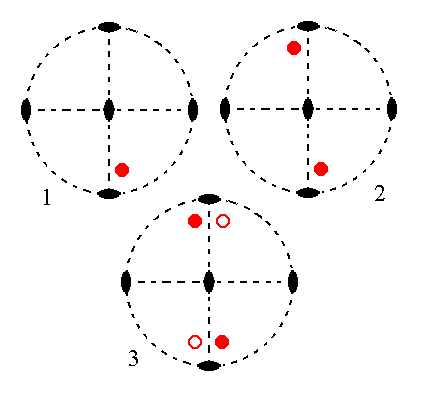
Figure 11.
(1). Position of the face a : nb : mc in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face. Both faces are upper faces.
(3). One of the two horizontal 2-fold rotation axes generates for each face an additional corresponding lower one. The final result then also already complies with the other horizontal 2-fold rotation axis, so the resulting face configuration (four faces) has 2 2 2 symmetry (i.e. the symmetry of our Class). It is a Rhombic Sphenoid.
The face a : b : ~c is vertical. It generates a hemihedric rhombic protoprism when subjected to the symmetry elements of the present Class : The face is duplicated by the action of the vertical 2-fold rotation axis, giving two vertical faces. Each face is then again duplicated by a horizontal 2-fold rotation axis resulting in four vertical faces making up a prism. The other 2-fold rotation axis is then implied. See Figure 12.
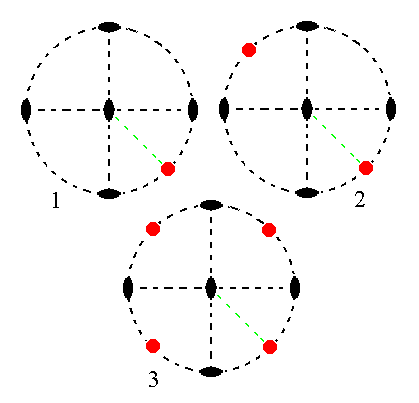
Figure 12.
(1). Position of the face a : b : ~c in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face. Both faces are vertical.
(3). One of the two horizontal 2-fold rotation axes generates for each face an additional one. The final result then also already complies with the other horizontal 2-fold rotation axis, so the resulting face configuration (four vertical faces) has 2 2 2 symmetry (i.e. the symmetry of our Class). It is a hemihedric Rhombic Protoprism.
The face na : b : ~c is also vertical. It generates a hemihedric brachyprism when subjected to the symmetry elements of the present Class : The face is duplicated by the vertical 2-fold rotation axis giving two vertical faces. Each of these faces will be duplicated by a horizontal 2-fold rotation axis resulting in four vertical faces making up a prism. The other horizontal 2-fold rotation axis is then implied. See Figure 13.
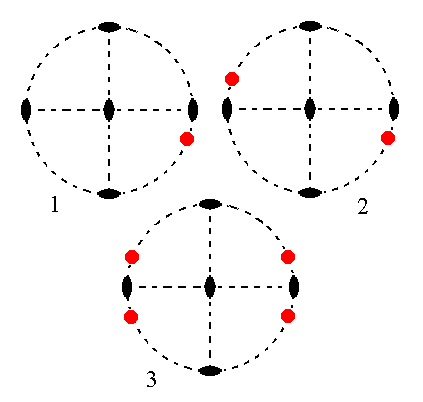
Figure 13.
(1). Position of the face na : b : ~c in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face. Both faces are vertical.
(3). One of the two horizontal 2-fold rotation axes generates for each face an additional one. The final result then also already complies with the other horizontal 2-fold rotation axis, so the resulting face configuration (four vertical faces) has 2 2 2 symmetry (i.e. the symmetry of our Class). It is a hemihedric Rhombic Brachyprism.
The face a : nb : ~c is also vertical. It generates a hemihedric macroprism when subjected to the symmetry elements of the present Class : The face is duplicated by the vertical 2-fold rotation axis giving two vertical faces each one of them is in turn duplicated by a horizontal 2-fold rotation axis resulting in four vertical faces making up a prism. The other 2-fold rotation axis is then implied. See Figure 14.
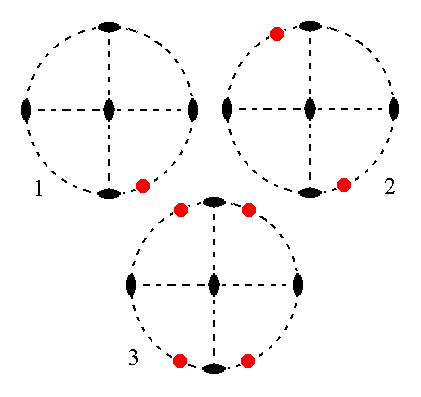
Figure 14.
(1). Position of the face a : nb : ~c in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face. Both faces are vertical.
(3). One of the two horizontal 2-fold rotation axes generates for each face an additional one. The final result then also already complies with the other horizontal 2-fold rotation axis, so the resulting face configuration (four vertical faces) has 2 2 2 symmetry (i.e. the symmetry of our Class). It is a hemihedric Rhombic Macroprism.
The face ~a : b : mc is parallel to the brachy axis. It generates a hemihedric brachydome when subjected to the symmetry elements of the present Class : The face is duplicated by the vertical 2-fold rotation axis giving two upper faces. Each of these faces is then rotated 1800 about the horizontal 2-fold rotation axis that is not parallel to those faces resulting in their obtaining lower counter faces, so we get two face pairs each consisting of an upper and lower face. These pairs together make up the brachydome. See Figure 15.
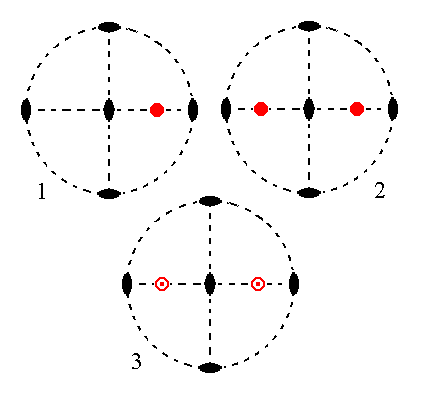
Figure 15.
(1). Position of the face ~a : b : mc in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face. These two faces are not parallel to each other but form an angle less then 1800.
(3). One of the two horizontal 2-fold rotation axes generates for each face an additional one just below it, resulting in four faces making up a Brachydome. The other rotation axis is then implied.
The face a : ~b : mc is parallel to the macro axis. It generates a hemihedric macrodome when subjected to the symmetry elements of the present Class : The face is duplicated by the vertical 2-fold rotation axis giving two upper faces making an angle smaller than 1800 with each other. Each of these faces becomes its lower counter face in virtue of the action of one of the horizontal 2-fold rotation axis resulting in four faces parallel to the macro axis making up a Macrodome. The other 2-fold rotation axis is then implied. See Figure 16.
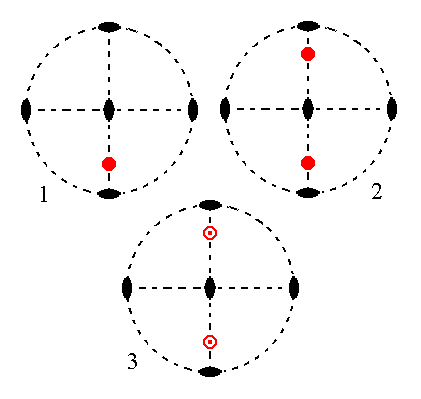
Figure 16.
(1). Position of the face a : ~b : mc in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face. These two faces are not parallel to each other but form an angle less then 1800.
(3). One of the two horizontal 2-fold rotation axes generates for each face an additional one just below it, resulting in four faces making up a Macrodome. The other rotation axis is then implied.
The face ~a : b : ~c is parallel to the brachy and vertical axes. It generates the hemihedric brachy pinacoid when subjected to the symmetry elements of the present Class : The face is duplicated by the action of the vertical 2-fold rotation axis, giving two parallel vertical faces parallel to the brachy axis, making up the brachy pinacoid. The other symmetry elements are then implied. See Figure 17.
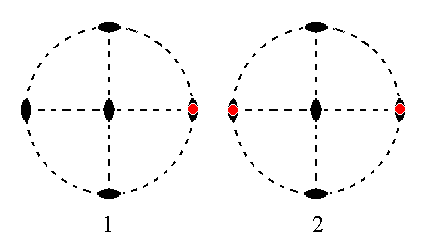
Figure 17.
(1). Position of the face ~a : b : ~c in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face parallel to the initial one. The other symmetry elements are then implied and we end up with a Form consisting of two vertical faces parallel to the brachy axis, a Brachy Pinacoid.
The face a : ~b : ~c is parallel to the macro and vertical axes. It generates the hemihedric macro pinacoid when subjected to the symmetry elements of the present Class : The face is duplicated by the vertical 2-fold rotation axis giving two vertical faces parallel to the macro axis making up the macro pinacoid. The other symmetry elements are then implied. See figure 18.
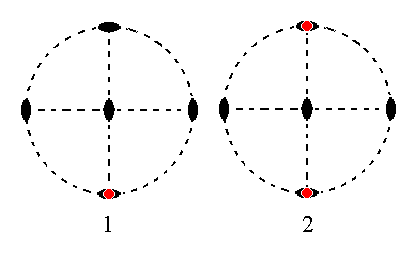
Figure 18.
(1). Position of the face a : ~b : ~c in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about the vertical 2-fold rotation axis by 1800 resulting in a second face parallel to the initial one. The other symmetry elements are then implied and we end up with a Form consisting of two vertical faces parallel to the macro axis, a Macro Pinacoid.
The face ~a : ~b : c, finally, is parallel to the brachy and macro axes which means that it is horizontal. It generates a hemihedric basic pinacoid when subjected to the symmetry elements of the present Class : The vertical 2-fold rotation axis does not generate new faces. One of the two horizontal 2-fold rotation axes duplicates this face resulting in a face pair consisting of an upper and a lower horizontal face, the basic pinacoid. The other horizontal 2-fold rotation axis is then implied. See figure 19.
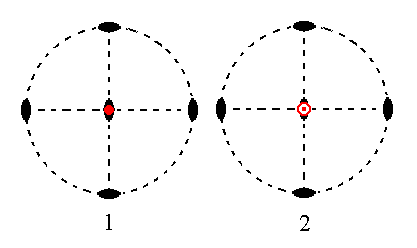
Figure 19.
(1). Position of the face ~a : ~b : c in the stereogram of the symmetry elements of the Rhombic-bisphenoidic Crystal Class.
(2). The face is rotated about a horizontal 2-fold rotation axis by 1800 resulting in a second face parallel to the initial one. The other symmetry elements are then implied and we end up with a Form consisting of two horizontal faces parallel to the brachy and macro axis, a Basic Pinacoid.
This concludes our exposition of the Rhombic-bisphenoidic Crystal Class, and with it our exposition of the Orthorhombic Crystal System.
To continue, klick HERE for Part One of the Monoclinic Crystal System (Class 2/m).