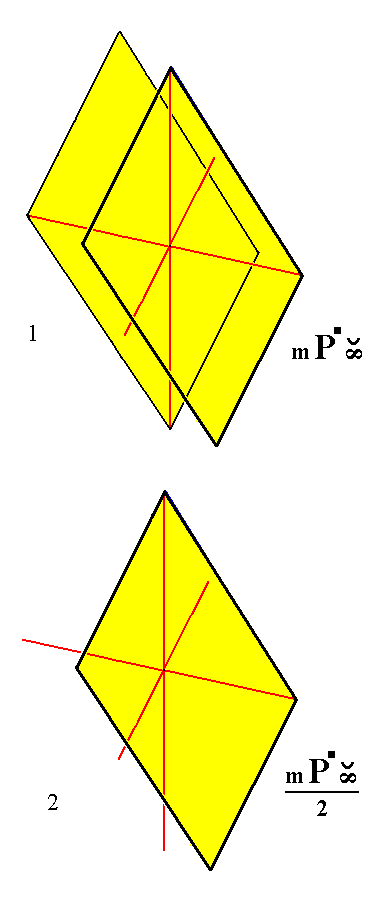The Forms of this Class can be derived from those of the Holohedric Division by applying hemihedric to them. We do this by suppressing the center of symmetry (being the only symmetry element possessed by Forms and crystals of the Holohedric Division). The effect of this suppression is a halving of the number of faces of each (holohedric) Form which here results in the fact that all the Forms of this new Class consist of only one face. So every Form is an open Form and must combine with other Forms (of the same Class, i.e. having the same symmetry) in order to be able to exist in real crystals.
Recall from Part One that the triclinic holohedric (simple) Forms were the following :
Generalized Triclinic Prototetartopyramid
Generalized Triclinic Brachytetartopyramid
Generalized Triclinic Macrotetartopyramid
Triclinic Protohemiprism
Generalized Triclinic Brachyhemiprism
Generalized Triclinic Macrohemiprism
Generalized Triclinic Brachyhemidome
Generalized Triclinic Macrohemidome
Triclinic Brachypinacoid
Triclinic Macropinacoid
Triclinic Basic Pinacoid
MEROHEDRIC APPROACH
We shall derive the Forms of the present Class (Triclinic-asymmetric Class, Hemihedric Division of the Triclinic System) by subjecting the listed holohedric Forms to hemihedric, which here means that the center of symmetry is suppressed. All the Forms of the holohedric division -- being parallel face pairs -- then end up as single faced Forms by suppressing one of their faces, which is equivalent to suppressing the center of symmetry. Each single face of a crystal belonging to the Asymmetric Class is thus an independent Form.
From the holohedric triclinic prototetartopyramid we can derive the triclinic proto-ogdopyramid when it is subjected to hemihedric, which here means that one of the two faces is suppressed. The result is a Form consisting of a single face, an ogdopyramid. See Figure 1.
 |
Figure 1. Derivation of a Triclinic non-primary Proto-ogdopyramid from a Triclinic Prototetartopyramid. (1). The non-primary Triclinic Prototetartopyramid. (2). Suppression of a face (here the lower one), resulting in a Triclinic Proto-ogdopyramid. The sign "2" in the Naumann symbol means that hemihedric is being applied. |
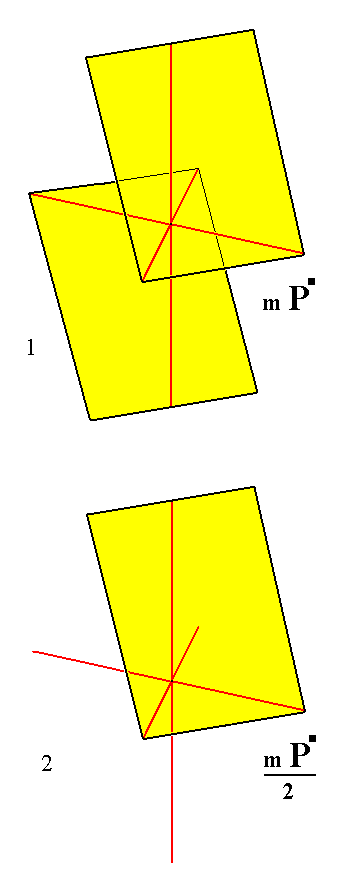
From the holohedric triclinic brachytetartopyramid we can derive the triclinic brachyogdopyramid when hemihedric is applied to it. Again the result is a single face.
 |
Figure 2. Derivation of a Triclinic non-primary Brachyogdopyramid from a Triclinic Brachytetartopyramid. (1). The non-primary Triclinic Brachytetartopyramid. (2). Suppression of a face (here the lower one), resulting in a Triclinic Brachyogdopyramid. The sign "2" in the Naumann symbol means that hemihedric is being applied. |
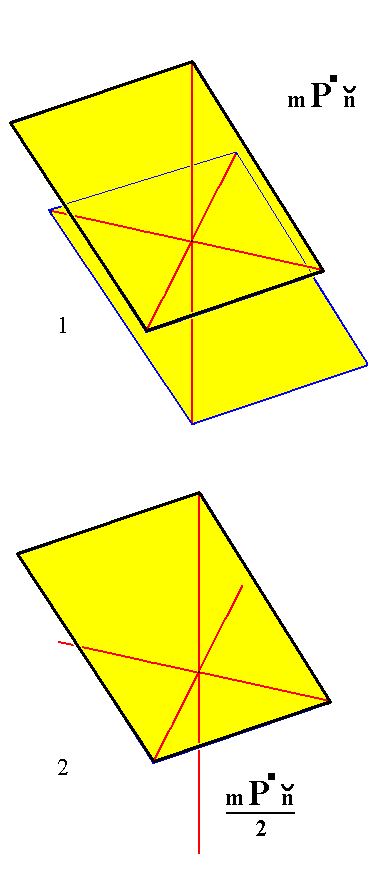
From the holohedric triclinic macrotetartopyramid we can derive the triclinic macro-ogdopyramid when it is subjected to hemihedric. This is accomplished by removing one of its faces. See Figure 3.
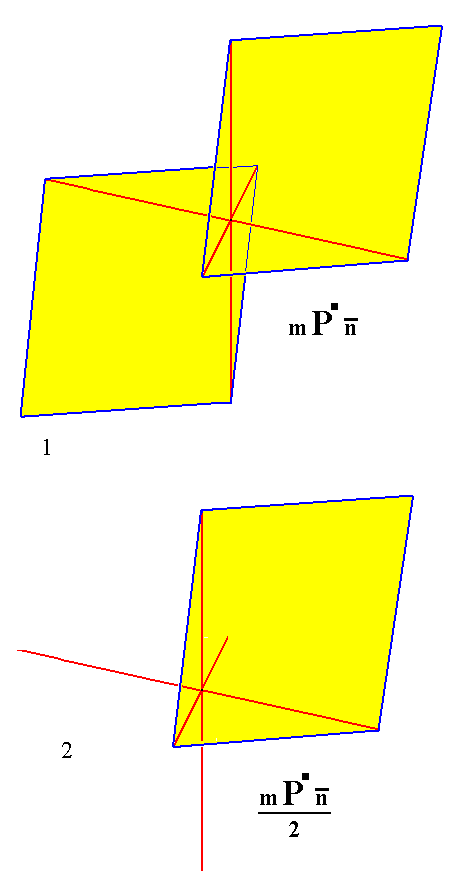
Figure 3.
Derivation of a Triclinic non-primary Macro-ogdopyramid from a Triclinic Macrotetartopyramid.
(1). The non-primary Triclinic Macrotetartopyramid.
(2). Suppression of a face (here the lower one), resulting in a Triclinic Macro-ogdopyramid.
The sign "2" in the Naumann symbol means that hemihedric is being applied.
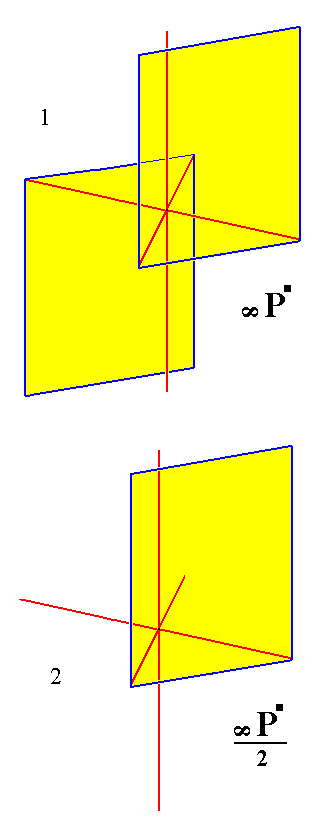
From the holohedric triclinic protohemiprism we can derive the triclinic prototetartoprism when it is subjected to hemihedric. This is accomplished by dropping one of the faces. See Figure 4.
 |
Figure 4. Derivation of the Triclinic Prototetartoprism from the Triclinic Protohemiprism. (1). The Triclinic Protohemiprism. (2). Suppression of a face (here the lower one), resulting in the Triclinic Prototetartoprism. |
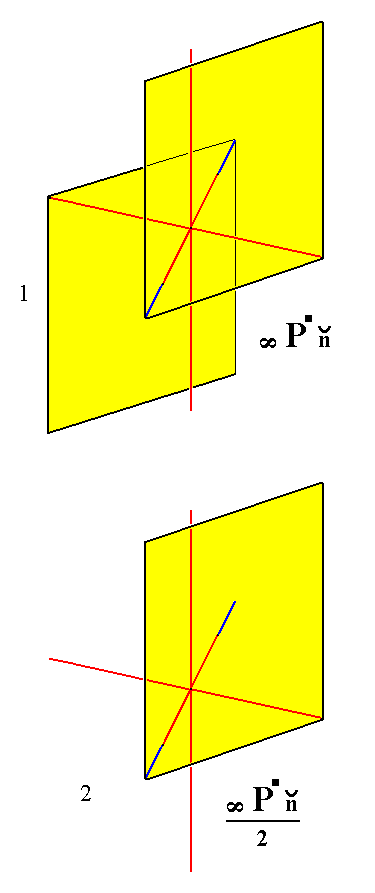
From the holohedric triclinic brachyhemiprism we can derive a triclinic brachytetartoprism when it is subjected to hemihedric. This is accomplished by dropping one of its faces. See Figure 5.
 |
Figure 5. Derivation of the Triclinic Brachytetartoprism from the Triclinic Brachyhemiprism. (1). The Triclinic Brachyhemiprism. (2). Suppression of a face (here the lower one), resulting in the Triclinic Brachytetartoprism. |
From the holohedric triclinic macrohemiprism we can derive a triclinic macrotetartoprism when it is subjected to hemihedric. This is accomplished by dropping one of its faces.
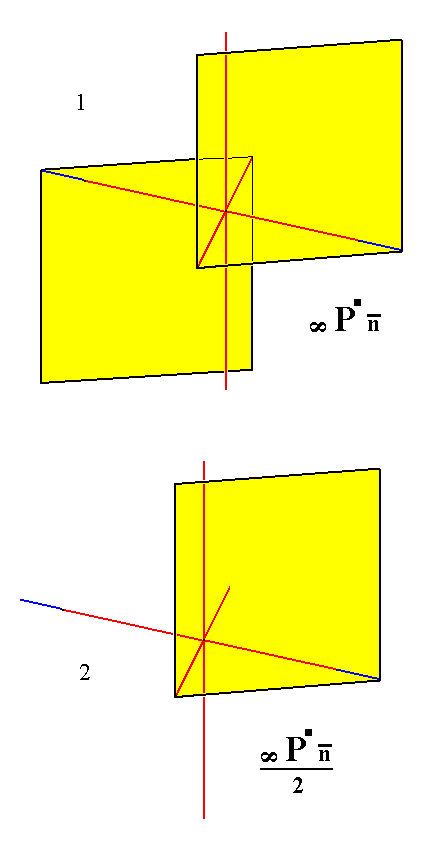
Figure 6.
Derivation of a Triclinic Macrotetartoprism from a Triclinic Macrohemiprism.
(1). The Triclinic Macrohemiprism.
(2). Suppression of a face (here the lower one), resulting in a Triclinic Macrotetartoprism.
From the holohedric triclinic brachyhemidome we can derive a triclinic brachytetartodome when it is subjected to hemihedric. This is accomplished by suppressing one of its faces. See Figure 7.
 |
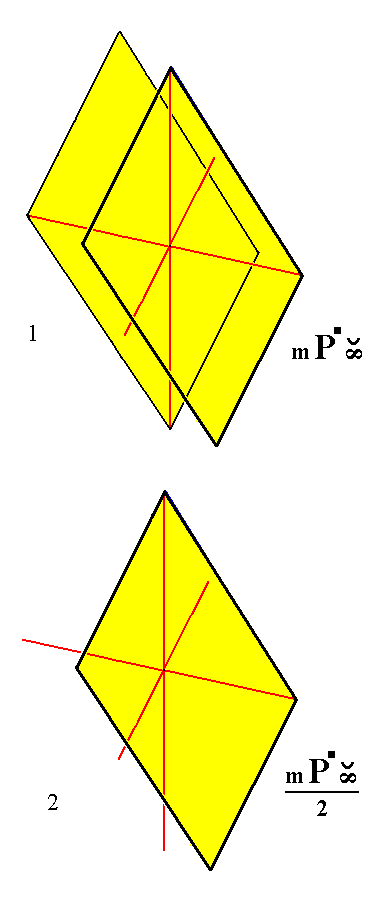Figure 7. Derivation of the Triclinic Brachytetartodome from the Triclinic Brachyhemidome. (1). The Triclinic Brachyhemidome. (2). Suppression of a face (here the lower one), resulting in the Triclinic Brachytetartodome. |
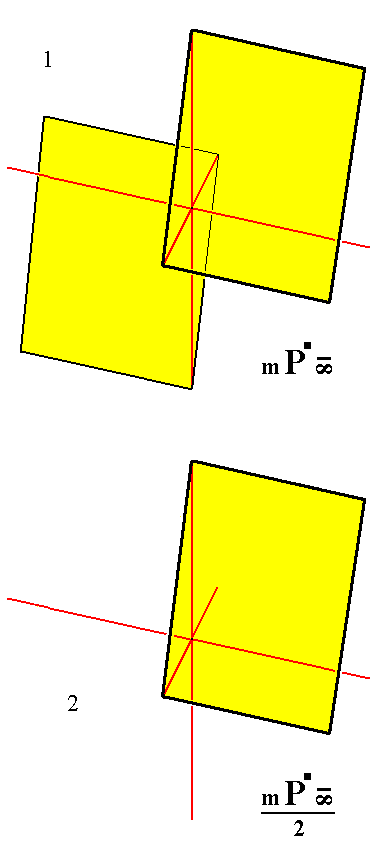
From the holohedric triclinic macrohemidome we can derive the triclinic macrotetartodome when it is subjected to hemihedric. This is accomplished by suppressing one of its faces. See Figure 8.
 |
Figure 8. Derivation of the Triclinic Macrotetartodome from the Triclinic Macrohemidome. (1). The Triclinic Macrohemidome. (2). Suppression of a face (here the lower one), resulting in the Triclinic Macrotetartodome. |
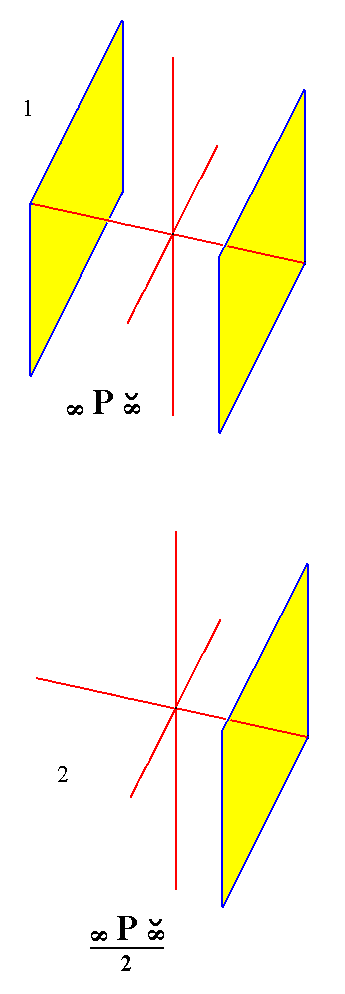
From the holohedric triclinic brachypinacoid we can derive the triclinic brachyhemipinacoid when it is subjected to hemihedric. This is accomplished by suppressing one of its faces. See Figure 9.
 |
Figure 9. Derivation of the Triclinic Brachyhemipinacoid from the Triclinic Brachypinacoid. (1). The Triclinic Brachypinacoid. (2). Suppression of a face (here the left one), resulting in the Triclinic Brachyhemipinacoid. |
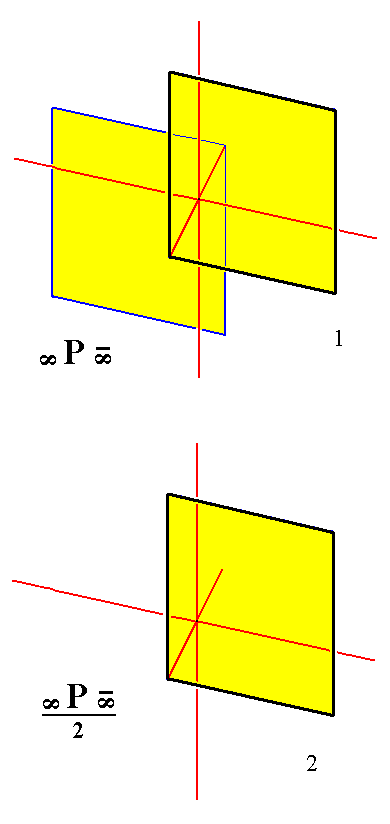
From the holohedric triclinic macropinacoid we can derive the triclinic macrohemipinacoid when it is subjected to hemihedric. This is accomplished by suppressing one of its faces.
 |
Figure 10. Derivation of the Triclinic Macrohemipinacoid from the Triclinic Macropinacoid. (1). The Triclinic Macropinacoid. (2). Suppression of a face (here the back face), resulting in the Triclinic Macrohemipinacoid. |
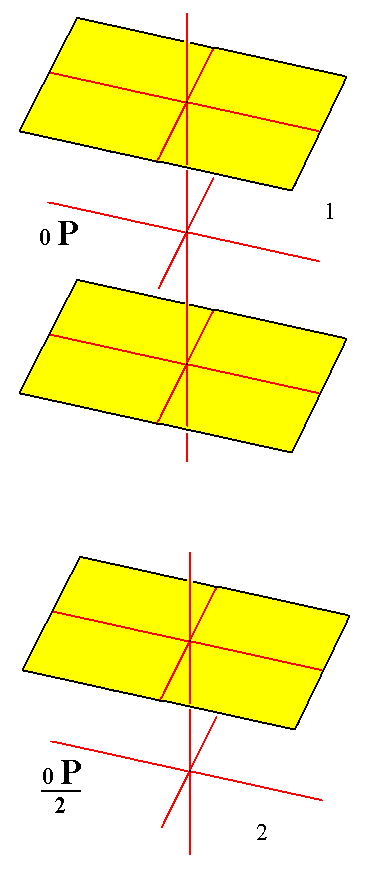
From the holohedric triclinic basic pinacoid, finally, we can derive the triclinic pedion when it is subjected to hemihedric. This is accomplished by suppressing one of its faces.
 |
Figure 11. Derivation of the Triclinic Pedion from the Triclinic Basic Pinacoid. (1). The Triclinic Basic Pinacoid. (2). Suppression of a face (here the lower one), resulting in the Triclinic Pedion. |
This concludes our derivation of all the Forms of the Triclinic-asymmetric Crystal Class.
Every Form of this Class consists of a single face, so they all are open Forms and can only exist in real crystals when combined with each other such that a space is fully enclosed.
FACIAL APPROACH
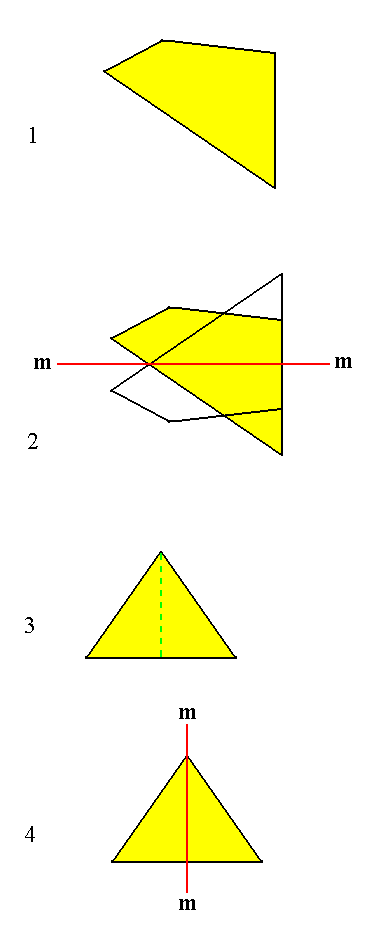
We will now derive those same Forms from the basic faces compatible with the Triclinic Crystal System, by subjecting those faces one by one to the symmetry elements of the present Class. This Class, however, does not have any symmetry elements that could multiply any face, because the only symmetry element is a 1-fold rotation axis. Such an axis is in fact no symmetry element at all because an object, possessing only such an axis, does not have each of its parts -- that do not lie on the symmetry element itself -- mapped onto another by any symmetry operation. The parts are instead only mapped onto themselves by the 1-fold rotation axis, the action of which is a rotation of 3600 about it . In Figure 12 the fact that the parts are not mapped onto other parts is shown for two-dimensional objects with respect to the symmetry operation of reflection.
 |
Figure 12. (1). A two-dimensional asymmetric object. (2). Reflection of the object in whatever mirror line ( m ) does not map every part of it -- not lying on the mirror line -- onto another part of it. (3). A two-dimensional symmetric object. (4). Reflection in the mirror line m does map every part of it -- that does not coincide with the mirror line -- onto another part of it. |
It is now clear that when we subject a face to the symmetry elements of the present Class the resulting Form is that same face. So all the basic faces are at the same time Form types. We will show these Forms in stereographic projection.
(For the stereographic projection of triclinic crystals see Part One).
Recall from Part One that the basic faces compatible with the Triclinic Crystal System were the ones enumerated in the following list. In this list we now accompany each basic face with the Form it represents in the present Class :
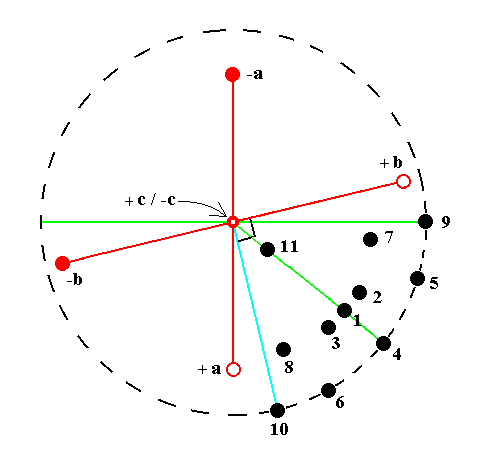
Figure 13. Position of all the basic faces of the above list (given by the numerals in that list) in the stereogram of the symmetry elements of the Triclinic-asymmetric Crystal Class. Each basic face is at the same time a Form of the Class.
Also indicated are the projections of the piercing points (through the projection sphere) of the brachy, macro and vertical axes (i.e. the crystallographic axes).
This concludes our exposition of the Triclinic-asymmetric Crystal Class, and with it our exposition of the Triclinic Crystal System.