

Go to the HOMEPAGE of this site, so that you can navigate through it, and find my e-mail address.
If your browser does NOT support FRAMES (The current page does not have them, but others do), please click HERE . You will arrive at the HOMEPAGE of this site (without FRAMES). From there you can navigate through this website by means of the links in the CONTENTS-section.
to bottom
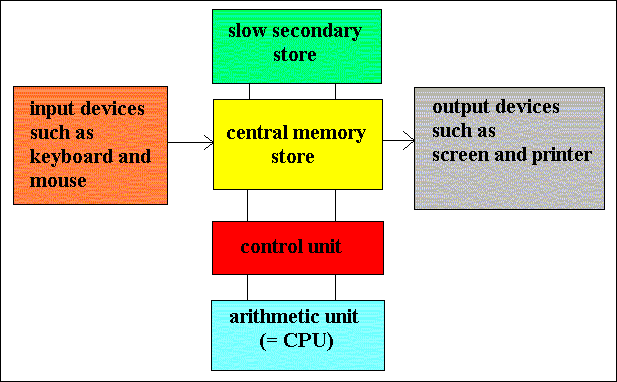
Figure 1. Von Neumann's computer architecture -- the layout of a typical serial machine. Except with respect to input and output devices, the information-flow is in a back-and-forth fashion.
To program such a computer, in order that it will solve a certain problem or generate some desired result, the programmer first writes an algorithm, which is a solution of the problem in the form of a sequence of steps, written in ordinary language. This algorithm is then coded into a suitable programming language that will enable the computer to ' understand ' and successfully execute the corresponding instructions. Usually, this involves one of the ' higher ' programming languages, so called because they are reasonable close to human language. But because the Central Processing Unit (CPU) is composed of a set of Boolean logic circuits, it is capable only of performing elementary arithmetic operations such as addition, subtraction, multiplication, and so on. Thus the original programming language fed into the computer must be first converted by means of an interpreter (translates one line of code and executes it, then translates the next line, etc.), or a compiler (translates the whole program and then executes it) into a machine-readable assembly language (instructions, coded in this assembly language are then directly translated into machine-code, that consists of the electronical equivalents of 0's and 1's) . Only then the machine is able to execute the fed-in instructions.
The input is coded up in memory, which is a grid of electronic on-off switches. The processor, which is a chip of integrated circuitry, alters what is in the memory, resulting in a different on-off pattern of switches, and then the output decodes and displays the new contents of the memory. So the actual computation consists of the processor's activities on the memory. Accordingly the processor and the memory stand in mutual contact with each other.
Turing Machines
Now exactly what is it that the processor has done? [See among other sources, RUCKER, Mind Tools, 1988]
Suppose [PETERSON, pp. 195] a Turing Machine must add two integers (this accordingly is a special Turing Machine -- out of many possible -- that specializes in executing this particualer task, the adding of any two whole numbers). We can represent such a whole number by a consecutive series of BLACK cells, for example the number 3 can be represented by three consecutive BLACK cells on the tape, and the number 4 can be represented by four such cells.
If we now want to ADD these two numbers, we write them both on the tape, with a WHITE cell in between. When we think of the cell-states as being either OFF (= WHITE) or ON (= BLACK), then our INPUT will be written on the tape as follows :
...00011101111000...
In order to ADD these numbers the machine fills in the blank cell, giving :
...00011111111000... ,
and then goes to the end of the string (of 1's) and erases the last 1 in the row, which results in the correct answer, namely a consecutive series of seven 1's :
...00011111110000...
An action table is needed to instruct the machine how to perform this addition (The foregoing was just an algorithm, a recipe, that still must be translated into an executable program). The table's first column gives the machine's possible internal states, and the first row lists all the cell-states being used (in our case the cell-states BLACK and WHITE).
Cell-state encountered
BLACK WHITE
(Internal) State 0 move right, get in state 0. put BLACK, move right, get in state 1.
(Internal) State 1 move right, get in state 1. move left, get in state 2.
(Internal) State 2 erase, stop.
Each combination of (internal) State and Cell-state specifies what, if anything, needs to be done to a cell, in which direction to move after the action, and the (internal) state of the machine, that is, which set of instructions it will follow for its next move.
Each one of these five instructions implies, among other things,











Figure 2. At each step, a Turing Machine may move one space to the left or right. By following a simple set of rules, this particular machine can add two whole numbers. The strategy of this particular machine is : Starting with separate groups of -- as in the example -- three and four BLACK cells, and ending up with one group of -- as in the example -- seven BLACK cells.
The same action-table can generate the sum of any two whole numbers, no matter what their size, as long as it is finite. But adding two numbers such as 49985 and 51664, by itself, would require a tape with at least 100000 cells. To be capable of adding any two numbers, the tape would have to be infinitely long, which does however not mean an actually infinite tape, but only a potentially infinite tape, which means that what ever the length of the tape already is, we can always add some tape if necessary.
Similar tables can be worked out for subtraction and for practically any other mathematical operation. The sole condition is that the number of internal states of the machine, and the number of different cell-states listed in the action-table, is finite, which ensures that a routine, mechanical process can do the job.
For every calculation a digital computer can perform there is a corresponding Turing machine which can do that same calculation. Let us consider some more of such Turing Machines. In expounding them we will use the above notation :
1XL2
2BR1
At the start the machine enters state 1 and reads a left-most BLACK cell. So it must execute the first instruction, which means it must go one cell to the left and enter state 2. There it encounters a WHITE cell, so it must now follow the second instruction, which means that it must move one cell to the right and enter state 1. There it finds a BLACK cell, so it must follow the first rule, i.e. it has returned to the original situation, and from now on these actions will be repeated ad infinitum.
If we denote the number of the (particular) machine's non-zero (internal) states with K, then the machine's total program contains at most 2K instructions, each of which begins with one of the 2K possible prefixes 1B--, 1X--, 2B--, 2X--, ..., KB--, KX--. This follows from the fact that any time the machine is on, its state is one of the numbers 1, 2, ..., K, and the cell it is examining is either a B or an X. Each " -- " can be filled in 4(K + 1) ways, because, for to fill in the last entry of " -- " we have K + 1 possible internal states (now including the 0-state), and for to fill in the first entry of " -- " we have four possible symbol-types : X, B, L and R.
This makes for [4(K + 1)]2K possible programs (action-tables) in all, i.e. 4(K + 1), multiplied with itself 2K times.
Let me explain this last assessment.
When we have, say, three symbol-types, a, b, c, and when we want to make strings, each consisting of four such symbols, then we can ask how many such strings are posible.
For the first entry of such a four-symbol string we have three possibilities, a, b, or c.
For the second entry we also have three possibilities, a, b, and c.
So each of the possible three first-entries has three possibilities with respect to the second entry. That makes 3 x 3 = 9 possibilities.
For the third entry of the four-symbol string we again have three possibilities, a, b, and c.
So each of the nine possibilies regarding the first two entries has three possibilities regarding the third entry, so that makes 3 x 9 = 27 possibilities.
For the fourth (and last) entry of the string we again have three possibilities, a, b, and c.
So each of the twenty-seven possibilities regarding the first, second and third entries has three possibilities regarding the choice of the fourth entry of the string, and that makes 3 x 27 = 81 possibilities in total four a four-symbol string using three different kinds of symbol.
81 equals 3 x 3 x 3 x 3 = 34. It is easy to generalize on that :
The number of possible strings, consisting of S different types of symbols, and with a length of L symbols equals SL.
Applying this to the assessment of the number of possible Turing Machine programs (action-tables) in dependence on the number of non-zero internal states, we can say the following :
A Turing Machine program can be considered as a string of instructions. Each instruction, like for instance 2XR1, can be interpreted as a conditional statement of the form IF .... THEN. The first half represents the condition to be satisfied, the second halve represents the instruction proper. In the above example 2X is the condition, and R1 is the action to be taken (go one cell to the right and enter internal state 1). We have 4(K + 1) different kinds of instruction proper, which we can call ' symbols'. These symbols must be carried by at most 2K instructions. So the length of the symbol-string is 2K. It follows that the number of strings with length 2K, consisting of 4(K + 1) different symbol-types equals
[4(K + 1)]2K, and this is thus the number of possible Turing Machine programs.
This is quite a large number even for small K's : for K = 2 it is already about twenty thousand, but the number of possible K-state Turing Machines is finite, and for large K, the value is roughly the same size as K2K. Of course an instruction (in a program),like for instance 3XB2, can be used more than one time during the running of the program.
Turing Machines can just do about anything. It can perform the same numerical tasks as any digital computer, but in general it is extremely slow. The importance therefore of the Turing machine is its being the fundamental concept of any digital computer.
We are now ready to describe a few Turing machines. A Turing machine computes a function
T(X) = Y, where X is some input and Y the output. We shall confine ourselves to the manipulation of non-zero natural numbers, thus the numbers 1, 2, 3, 4, ... .
Such a function could be : T(N) = N + 3.
This means that we can give any such natural number N as input, and the Turing Machine will compute the addition of 3, i.e. it will compute N + 3. This can be done with a five-state Turing Machine, that adds three BLACK cells to the right end of the starting string (of BLACK cells) [See RUCKER, 1988, Mind Tools, p. 232] :
Let us execute this program, for N = 2. Thus we will compute T(2) = 2 + 3. [said in a more elegant way : We will compute the function T(N) = N + 3, for N = 3].
The input is XX, two BLACK cells on the tape.
To start with, the machine is placed on the left-most BLACK cell and set in internal state 1.
So the first instruction to execute is one (from the list) beginning with 1X, thus 1XR1. This will cause the machine to move one cell to the right while the machine remains in state 1. It encounters a BLACK cell, so again the instruction beginning with 1X, thus 1XR1, must be executed. The machine goes one cell to the right, encounters a WHITE cell, and remains in state 1. Now the machine must look for an instruction that begins with, 1B, hence 1BX2. This tells the machine to make that cell BLACK and to enter state 2. Now the machine must look in the list for an instruction that begins with 2X, it finds it : 2XR3. According to this instruction the machine must move one cell to the right and enter state 3. It encounters a WHITE cell, so the machine must look for an instruction beginning with 3B, this is instruction 3BX3. So it must make this cell BLACK and remain in state 3. Now it must look up an instruction beginning with 3X, and that is 3XR4. Again it must move one cell to the right and enter state 4. It encounters a WHITE cell, so it must find an instruction beginning with 4B, that is 4BX0, so the machine must make this cell BLACK and turn itself off. The calculation is completed, we started with two consecutive BLACK cells and ended up with five consecutive BLACK cells.
A next example of a Turing machine is a machine with a program that computes the function
T(N) = N + N. This programm uses the original number of BLACK cells (i.e. the input, the value of N) as a counter : it erases them one by one and replaces each of them with two new BLACK cells. When the original BLACK cells are all erased then the program will halt, and the computation is done. This can be performed with an 8-state Turing machine, one 0-state (the STOP sign) and 7 non-zero states, so K = 7.
Let us calculate the above function for N = 3, thus the calculation
T(3) = 3 + 3 :















The program now starts all over again, beginning (again) with the first instruction.
This repetition will go on until all the original N's are erased and replaced --
at the end of the string -- by two N's each :








As can be seen, when we anticipate to need more tape, we just add more tape.
In this way the memory (capacity) of the Turing Machine is potentially infinite.








Again the program will revert to the first instruction.

















The program now sees that all the original N's are erased.

The machine will now turn itself off, and the calculation is completed.
We started off with X X X (input), and ended up with X X X X X X (output).
It took 47 steps for this machine to accomplish this, i.e. to calculate
the function T(N) = N + N for N = 3.
A Turing Machine can become a universal Turing Machine, U, because it can (be made to) accept any program P and data D.
The binary number system is just a different notation for numbers. Whereas the conventional (denary) notation uses powers of 10 (for example 358 = 3 x 102 + 5 x 101 + 8 x 100), the binary notation uses powers of 2 (for example 1101 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 13 in denary) [ a number raised to the 0th power always equals 1. Proof :
a0 = ab-b = ab divided by ab = 1 ].
Because a computer-design always consists of a pattern of switches that are either ON or OFF, the binary number system of notation is very convenient for coding data and instructions.
Each Turing machine characterizes itself by its set of instructions. It will start to operate when we feed in some data. The data will consist of a number (or numbers) on which a certain operation will be carried out by the machine according to its set of instructions.

Figure 3. A twelve-state Turing machine. The horizontal bar symbolizes the possible different internal states the machine can be in. The program is the set of instructions (here applying a notation we used earlier). The machine can move along the tape one cell at a time. It can read its current state and the state of the cell it is visiting.
( After RUCKER, 1988, Mind Tools.)
Since a Turing Machine has only a finite number of distinct internal states it cannot be expected to ' internalize ' all the external data nor all the results of its own calculations. Instead it must examine only those parts of the data or (parts of results of) previous calculations that it is immediately dealing with (i.e. which it locally encounters), and then perform whatever operation it is required to perform on them. It can note down, perhaps in the external storage space, the relevant results of that operation, and then proceed in a precisely determined way to the next stage of operation.
Let us give a first coding scheme (that will later be altered, in order to be suitable for the construction of a universal Turing machine) for these instructions :
A typical instruction could then be
0O implies 0OR
This instruction means :
If the machine finds itself in state 0, and if it reads an unmarked cell, then it must remain in state 0, and put a O, i.e. leave that cell unmarked.
Another typical instruction could be
11O implies 1001011L
This instruction means :
If the machine finds itself in state 11, and reads an unmarked cell, then it must enter state 100101, and put a 1, i.e. it must mark that cell.
After the machine has executed such an instruction, it will read its new state, and it will read the cell on which it is now placed, namely whether this cell is marked or unmarked. These two readings together determine which instruction is to be executed next.
Our aim is finally to code the instruction list using only the symbols 0 and 1, because that will be convenient for a computer (of which the Turing machine is the bare concept) that operates with swiches that can either be ON or OFF. So we must code the symbols L, R, STOP and punctuation marks (like commas, or marks that indicate the termination of, say, an instruction) with the aid of the symbols 0 and 1. Also any kind of other mathematical symbols must be coded by means of only these two symbols. But how is it possible, using only strings of 0's and 1's, to distinguish instructions and all kinds of other marks from just numbers? Where does the string of 0's and 1's representing not a number end, in a for the machine recognizable way, and then followed by a string of 0's and 1's which represents a number, and where does this string in turn end, to be followed by yet another string of 0's and 1's representing again not a number? Further there will be Turing Machines that need as input two or more numbers, for example a Turing Machine that should calculate the highest common factor of two given numbers. Also, there will be operations that will output a pair of numbers, for example division with a remainder. All these numbers must be separated somehow from each other, for example by means of a comma. So we must find a way how to code items like a comma, an instruction, a mathematical symbol, by means of the symbols 0 and 1.
This can indeed be done by the following method :
Because representing a number N just by N 1's will be very inefficient for large numbers, we first of all are going to use the binary number notation (thus not just using two symbols instead of ten, but a complete notational scheme). This notation uses only 0's and 1's, but the position of them in the string indicates their value as has been explaned above. So for example the number 29 is 11101 (1 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20). In order to code numbers (in binary notation) as well as instructions, commas, etcetera into strings of 0's and 1's we could apply the following transformations :
Later on we will change this coding a little (they are of course optional, but once settled we must stick to it). We call this : coding by expansion [PENROSE, 1990, The Emperor's New Mind ].
First of all we shall concentrate on the first three transformations, that garantee the unambiguous coding of a sequence of more then one number. Let us take as an example the number-sequence
5, 13, 0, 1, 1, 4,
The last comma serves to mark the end of the sequence, that otherwise would not be clear when this sequence is transformed into a sequence of 0's and 1's, because the tape of the Turing Machine must be potentially infinite in both directions and thus looks like this :
.................000000000 any number coded with 0's and 1's 00000000.................
The Machine must know for sure that the number sequence has ended, and that there will not appear any 1 further down the (potentially) infinite series of 0's on the right.
Let us first change the denary notation of the numbers above into binary. We get the sequence
101, 1101, 0, 1, 1, 100,
Now we will code this sequence by expansion according to the above transformations. This will generate the following string (for convenience we color the coded commas) :
...00001001011010100101100110101101011010001100000....
It is clear that by this method of coding the actual NUMBERS appear as sequences of 0's and 1's in such a way that there will never appear more than one 1 directly after each other (because 0 is coded as 0, and 1 is coded as 10). So we can now use sequences-of-more-than-one-1-directly-after-each-other -- and terminated with a 0 ( as can be seen in the above transformation list), to code all kinds of non-numbers, like we just did concerning the comma (that separates numbers) which was coded as 110. Other sequences, like 1110, 11110, etc. can now be used for other symbols, for instance instructions, the STOP sign, mathematical symbols, etc.
One more final point should be made about this coding. In the binary notation (as in the denary notation) one or more 0's in front of a number is redundant, resulting in the fact that for example
0001101 is equal to 1101, and also 000 (or 00 or 0000, etc.) is equal to 0. In not-expanded (but binary) notation this could lead to confusions as to whether a 0 separates two numbers or whether it belongs to one or the other number or whether it is a part of one number. With the expanded binary notation such confusions cannot occur, because of the possibility to use a coding for commas. But then we even do not need to explicitly write down a 0 between two commas, like we see in the above sequence, where the third number is a 0. We can simply code ,0, as two commas directly next to one another (,,). In expanded notation this would give
...000110110000...
Thus the above set of six numbers can finally be coded as :
...0000100101101010010110110101101011010001100000....
This string has accordingly one 0 missing in comparison with the string we had before.
By means of this coding by expansion we can conveniently code DATA (and output) for a Turing machine, also when they consist of more than one number.
Besides the natural numbers [the numbers 0, 1, 2, 3, ... ] on which we have concentrated so far, there are other numbers, like negative numbers (like -34), fractions (like 23/5), numbers as finite decimal expressions (like 3. 54789), and numbers as infinite decimal expressions (like pi, 3.14159265358979...). When we must code for negative numbers, then we must have a code for the minus-sign, and such a code can easily be provided (using expanded binary notation) by sequences of consecutive 1's, terminated by a 0, like 1111110. The same can be said for fractions. There we need a code for the / sign. Also a finite decimal expression can be coded as a division, using the (coding for the) / sign again.
For example 3. 476 = 3476/1000.
So all these numbers can be handled by Turing Machines.
However numbers that must be represented by infinite decimal expressions can present difficulties. We can conceive of a Turing machine churning out all the successive digits of the number pi (that must be represented by an infinite string of symbols, decimal or otherwise), and consequently running forever. But this is not allowed for a Turing Machine, because when the machine does not halt we don't know whether the result will be changed during further calculation (the machine can visit previous outputs and rework these). Only after the machine has halted we can trust the result.
But there is a way to conceive of a legitimately specified Turing machine that can generate one digit of pi after another : It must produce the 1st digit by acting on the number 1, then it must produce the 2nd digit by acting on the number 2, then it must produce the 3rd digit by acting on the number 3, etcetera. So when the machine starts to act on a next number we know that the calculation of the previous digit was wholly completed.
Until now we have described the general construction of one or another specific Turing Machine. With " specific " we mean a Turing Machine supplied with a special program, i.e. supplied with a special set of instructions (instructions like for instance
11010O implies 10011R ) in order to perform a special task, for example multiplying any given number with 25. Such a machine has this set of instructions internalized (see figure 3., but in fact more so than the figure suggests) -- this set of instructions are part of its hardware, while the data is fed in by the tape as input, and the result will be placed on the tape as output.
We will now try to describe a Universal Turing Machine.
In such a machine we want to externalize the program, so that it becomes software for a universal hardware machine. We can do this by coding the set of instructions for an arbitrary Turing machine T into a string of 0's and 1's that can be represented on a tape, and becomes as such externalized, and so part of the input for the machine. As such it then is not a part of the machine anymore, but an optional input -- a program, instructing the universal machine (how) to execute a certain task. This tape, i.e. this program, is accordingly used as the initial part of the input for the universal machine U which then acts on the remainder of the input (the data) just as T would have done. This universal Turing Machine is a universal mimic. The initial part of the tape provides the full information for the universal machine U that it needs for it to imitate any given machine T exactly. This universal Turing machine must be instructed how and when to read the initial part of the tape and how and when to shift the reading-activity to the second part (the data part) of the tape. The relevant instructions for performing these activities form the instruction-set of the machine U itself, i.e. its own instruction-set, that we can interpret as its hardware (its wiring-circuit).
To see how we can conceptually construct such a universal Turing machine, we need a way of numbering Turing Machines. To accomplish this we must start with a general way of coding the instruction-set of an arbitrary Turing machine. Let us, to understand the procedure, take the Turing machine that will add ONE to any given input. Let us call this Turing machine
XN + 1. This Turing machine acceps a number, written in expanded binary notation (where, as we learned above, 0 becomes 0, and 1 becomes 10) and acts on this number leading to an output that must also be considered as expanded binary, and this number has ONE added to the original number (whether we interprete input and output as ordinary binary or expanded binary).
In this particular Turing machine, XN + 1, the instruction-set still figures as its hardware and is (interpreted as) ' soldered ' into the machine (such a machine can only perform one task, in this case ADDING ONE to a given number). Therefore the instruction-set is not coded using only 0's and 1's. The tape only consists of the data, in this case one number, written in expanded binary. The instruction-set for the machine XN + 1 is as follows [See PENROSE, 1990, p. 60]
(recall that an instruction such as 110O implies 0OR means : If the machine is in state 110 (binary notation) and reads a O, then it must enter state 0 and move one cell to the right ) :
0O implies 0OR
01 implies 11R
1O implies 0OR
11 implies 101R
10O implies 11OL
101 implies 101R
11O implies 01STOP
111 implies 100OL
100O implies 1011L
1001 implies 1001L
101O implies 110OR
1011 implies 101R
1101 implies 1111R
111O implies 111R
1111 implies 111OR
When this machine is fed with a number N (in expanded binary notation) it will output a number (in expanded binary notation) N + 1.
When we now want this instruction-set to become just a program for the universal Turing machine, we must code this program into a sequence of 0's and 1's so that we can put it as marks on a tape (BLACK cells, or WHITE cells), and in this way externalize the instruction-set. To begin with, we do not have to distinguish between ordinary 0's and 1's and boldface O's and 1's as we see them in the above instruction-set, because those boldface figures occur only once in each condition of an instruction (i.e. the sequence of symbols before IMPLIES), and also only once in each action-term of an instruction (i.e. the sequence of symbols coming after IMPLIES) Thus for, say, 11O we can write just 110. We can further economize considerably by omitting the IMPLIES-term and also omitting all that comes before that term, relying instead upon the numerical ordering of instructions to specify what those instructions must be. Let me explain this.
The list of instructions can be ordered according to their conditions (the part of the instruction that precedes the IMPLIES-term) when we read them as binary numbers. When we want to use this ordering (i.e. the place of each instruction in an ordered list) then this ordering must not contain gaps, because in that case the specification, saying which instruction must be followed next, will be spoiled. So when there is such a gap then we must insert a dummie-instruction. Indeed in the list of instructions for the machine XN + 1 we miss (in the conditions) 110O, so we will insert a dummie-instruction : 110O implies 0OR . This results in a complete ordering of the list (the dummie-instruction will not be visited by this machine so it does not make a difference in its calculation-procedure). Let us give this list (including the dummie-instruction) and indicate its ordering by a series of consecutive indexes:
00R
11R
00R
101R
110L
101R
01STOP
1000L
1011L
1001L
1100R
101R
00R (dummie)
1111R
111R
1110R
Now we are ready to code these instructions into expanded binary according to the following list of transformations (recall that by coding in this way we are able to distinguish between numbers and non-numbers -- non-numbers are things like R, L, STOP, etc.) :
0 becomes 0
1 becomes 10
R becomes 110
L becomes 1110
STOP becomes 11110
Because these instructions are well separated by R, L and STOP, and correspondingly well separated by 110, 1110 and 11110 (because apart from them we can never encounter more then one 1's directly after each other) we can omit any 00 when this is all there is between two such signs (for example between R and L). So ... R 0 0 L ... -- where R is the last part of an instruction, and 0 0 L is the next instruction meaning : enter state 0, write a 0, and move one cell to the left -- can be written as . . . R L . . . , and thus coded as . . . 1 1 0 1 1 1 0 . . . .
It is also clear that 01, when that is all there is between two (separating) signs like R, L or STOP, can be replaced by 1, because then we see this 1 between two separating signs (like R, L or STOP) and the fact that before it stands nothing, can be interpreted as a 0 , so, for example
. . . R 0 1 L . . . can be replaced by . . . R 1 L . . . , and coded as . . . 1 1 0 1 1 1 1 0 . . . . In reading . . . 1 1 0 1 1 1 1 0 . . . the machine cannot be confused by the fact that it encounters . . . 1 1 1 1 0 . . . and interprets this (falsely) as " STOP", because then it reads . . . R STOP . . . , and because STOP itself already means R STOP, the machine would read R R STOP, which cannot be a proper instruction because in one and the same individual instruction the movement of the machine is only one cell (to the right or left), and not two times to the right, nor two times to the left, nor to the left and (then) to the right (because this latter is no movement at all and should not be coded).
The above already abbreviated instruction-list (including the dummie-instruction) for Turing Machine XN + 1 will accordingly look like this (written horizontally) :
R 1 1 R R 1 0 1 R 1 1 0 L 1 0 1 R 1 S T O P 1 0 0 0 L 1 0 1 1 L 1 0 0 1 L 1 1 0 0 R 1 0 1 R R 1 1 1 1 R 1 1 1 R 1 1 1 0 R
This is coded as the tape sequence :
11010101101101001011010100111010010110101
11101000011101001010111010001011101010001
1010010110110101010101101010101101010100110
To the left and to the right of this sequence we must think of a potentially infinite string of 0's.
We see that the sequence begins with 110 and ends with 110. We can leave out the initial 110, because this means 00R, representing the initial instruction
00 implies 00R that we assume (i.e. stipulate) common to all Turing machines, so that the device can start arbitrarily far to the left of the marks on the tape and run to the right until it comes up to the first mark (1).
Also we may delete the final 110, since all Turing Machines must have their descriptions ending this way, because they all end with R ( 110 ), L ( 1110 ) or STOP ( 11110 ). The machine will always start with reading an 110 in front of this economized sequence, and always read an 110 after this sequence.
When we moreover imagine to leave out the infinite strings of 0's to the left and to the right, then the resulting BINARY NUMBER (i.e. the resulting sequence interpreted as an ordinary binary number) is THE NUMBER OF THE TURING MACHINE, which in our case of the Turing machine XN + 1 is :
10101101101001011010100111010010110101 11101000011101001010111010001011101010001 1010010110110101010101101010101101010100
In standard denary notation, this particular number is :
450813704461593958982113775643437908.
Sometimes one loosely refers to a Turing machine whose number is N as the Nth Turing machine TN. Thus XN + 1 is the
450813704461593958982113775643437908th Turing machine.
In principle with each binary number should correspond a certain Turing Machine, which could perform a certain task. But many of them are not really genuine Turing machines at all because many of them turn out not to be defined unambiguously or run forever without giving a final output [See PENROSE, 1990, p.70/1].
So we have now succeeded in coding the instruction-set of any Turing machine into a string of 0's and 1's, and this string can be represented on a tape and serve as a program for a universal Turing machine. The machine reads this string by adding 110 at the beginning and at the end, and by interpreting this whole string as expanded binary it reads in fact its instruction-set. But of course this is not enough. Every Turing machine needs DATA, so also our universal Turing machine.
The DATA must be coded on the tape after the coding (sequence) of the instruction-set (the program), separated by the sign 111110. This coding of DATA must also be done by means of expanded binary, because sometimes we need more than one number as input, and these numbers must be separated by signs themselves also consisting of 0's and 1's only. Moreover one can have Turing Machines which operate directly on mathematical formulae, such as algebraic or trigonometric expressions. In these expressions all kinds of signs occur that are themselves not numbers, such as integrals sines and cosines. They all must be coded using only 0's and 1's. And this can be done conveniently by the method of expansion. And the Machine must accordingly read such a string as a result of this expansion. So far so good.
Besides the fact that the machine interprets such a string in such and such a way (in this case as the result of expansion), WE ourselves can (also) interprete (i.e. read) such a string in another way (namely for the purpose of generating a concept for a universal Turing Machine) :
Because the data-string always consists of 0's and 1's only, we can always (also) interpret it as just the representation of ONE binary number (We did this already with the string, representing the instructions, and in that way obtained the number of the Turing Machine). But because the series of 0's and 1's always ends up with an potentially infinite series of 0's it can as such not be interpreted as a definite binary number (the value of this number would be indefinitely large), so we must terminate it somewhere. Because now we interpret that string NOT as the result of expansion (which the machine does), we cannot interpret sequences as, say, 110, as commas, one of them terminating the data-string. One way of reading the string as an ordinary binary number could be by only reading this string till the last 1 appears, and including this last 1. But then our reading would result in odd numbers only. To remedy this problem we, in our effort to read the data-string as ONE number (the machine reads it another way), will NOT read the last 1, and then readings of both odd and even numbers are indeed possible. For example we can read the input-string
as the following binary number :
and the number
as the following binary number :
And this interpretation of the input-string can be used to generate the concept of the universal Turing machine, as follows :
Our discussion will first of all use only valid Turing Machines, i.e. correctly specified machines, which means that the machine, when turned on will come to a halt after a finite number of steps, and delivers an output.
We call the data-string, interpreted as a single binary number, the number M. When the Nth Turing Machine TN is fed with the number M, then it will, provided that this Turing machine is correctly specified, generate an output after a finite number of steps. This output can in fact be a complex expression containing all kinds of signs coded in expanded binary. But, just as was the case with the data-string, we can (also) interpret this output-string as representing ONE (ordinary) binary number. Let us call this number P.
So when we feed TN with M, then we get P. We can express this as follows :
But we can look at this relation in a slightly different way also. When we know the numbers N and M, then we can work out what P is, by seeing what the Nth Turing machine does to M. This particular operation is entirely algorithmic and can therefore be carried out by a Turing machine U. This machine U works on the pair (N,M) and outputs P.:
Since the machine U has to act on both N and M, and since we want to put both N and M on a tape, we need some way of separating the two. We can do this by the same type of sign we already use in N to specify things like R (110, L 1110, STOP 11110, etc.). So if we use a not yet used sign, say, 111110, to code for this separation-mark, then we can separate N and M easily. When the Machine is working after this mark, then it is working on the data, and here we can use for example 110 for coding a comma, and other such marks for other signs and symbols.
So it is now possible to code both N and M on the tape of U. When we start U it will work on M according to N, i.e. it simulates the Turing Machine TN. So this Machine U can simulate any Turing Machine, and thus is a Universal Turing Machine.
Let us quote an example, adapted from PENROSE, p. 73, for U simulating the eleventh Turing Machine, T11. We give this Turing machine T11 the number 722 as input. So we then have a Universal Turing Machine working on the numbers N and M, where N = 11 (denary notation) and M = 722.
When we express the number 11 in (ordinary) binary notation, then we get N = 1011. We know that the machine reads this sequence as being preceded by 110, and also terminated by 110. So it reads (we space the digits for clarity) :
This represents the action-parts of the instruction (i.e. the instruction-set, represented by the sequence of the -- ordered -- action-parts of the instructions) :
1 1 0 = R,
1 1 1 1 0 = STOP
Between these we find 1 0, that must be interpreted (read) as 1, because the expanded form of 1 is 1 0. So we have :
Before R we see nothing. This means that we must read this " nothing " as 0 0, because before signs like STOP, R, L, etc. we expect TWO symbols. Likewise we must interpret the 1 . Because before STOP we expect TWO symbols, we must interprete this 1 as 0 1. So we accordingly have :
This corresponds to the action-parts of two instructions, namely
00R means : enter internal state 0, write 0, and move one cell to the right.
01STOP means : enter internal state 0, write 1, move one cell to the right and stop (recall that STOP means RSTOP).
We know that each action-part (00R and 01STOP) must be connected with the term IMPLIES, and before that term the conditional-part of the instruction must be conceived present : the FIRST action-part must relate to the numerical FIRST conditional-part ( 00 ), the SECOND action-part must relate to the numerical SECOND conditional-part ( 01 )
[Recall that the full instructions are ORDERED according to the numerical value of the conditional-parts, which means that the machine, after having executed a complete instruction, knows which instruction to execute next. For example when, after having executed a complete instruction, it reads its internal state as 1101 (binary notation for 13), and it reads a marked (1) cell, then it must look for the 11011th instruction (in denary notation this is the 27th instruction). This next instruction to be executed can be found in the ordered list of action-parts, and the machine knows that the corresponding conditional-part is 11011, which means : IF the machine finds itself in state 1101, and reads a marked cell, then it must ..... ].
For our example we found that the conditional part of 00R is 00, and the conditional part of 01STOP is 01. So the complete instruction-set for T11, and consequently (the complete instructon-set, i.e. its program) for U (11, 722), is :
This instruction set means :
IF the machine is in internal state 0, and finds itself on a blank cell (it is stipulated that every Turing mache starts this way), THEN it must remain in state 0, write a 0, and moves one cell to the right. IF the machine is in internal state 0, and reads a marked cell, THEN it must move one cell to the right and switch itself off (recall again that STOP = RSTOP).
This instruction-set will now become the program (that could easily be replaced by another such program) of the Universal Turing machine U. This program (the instruction-set of T11) will be represented on the tape of U by the binary representation of the number 11 (N = 11) : 1 0 1 1. This number will be separated from the number M (M = 722) representing the data, by the sign 1 1 1 1 1 0 , and after this termination-sign should come the binary representation of 722, that is 1 0 1 1 0 1 0 0 1 0 , but this must be represented on the tape as 1 0 1 1 0 1 0 0 1 0 1 where the last 1 is readed as a termination-mark. So we feed U with the following string :
where,
. . . 0 0 0 is the initial blank tape,
1 0 1 1 is the binary representation of 11,
1 1 1 1 1 0 is the termination mark of N,
1 0 1 1 0 1 0 0 1 0 is the binary representation of 722,
1 0 0 0 . . . is the remainder of the tape.
What the Turing machine U would have to do, at each successive step of the operation of TN on M, would be to examine the structure of the succession of digits in the expression for N (i.e. reading the successive instructions for TN), so that the appropriate replacement (the calculation activities) in the digits for M (i.e. TN's ' tape ') can be made.
U's own list of instructions would simply be providing a means of reading the appropriate entry in that list (which is encoded in the number N) at each stage of application to the digits of the data-string as given by M.
There would admittedly be a lot of dodging backwards and forwards between the digits of M and those of N, and the procedure would tend to be exceedingly slow. Nevertheless a list of instructions for such a machine can certainly be provided [PENROSE, p. 73], and we call such a machine a universal Turing Machine. The machine U, when first fed with the number N, precisely imitates the Nth Turing machine.
Since U is a Turing Machine, it will itself have a number, i.e. we have
for some number u.
At last we have described one of the possible versions of a UNIVERAL TURING MACHINE.
We can feed this machine with any correctly specified program (the number N), and then it will execute the task that the program dictates. We can perhaps interpret its own instruction-set (described with the number u ) as the hardware of the machine, i.e. the totally internalized specification, that should be realized by means of electrical circuits inside the machine [See PART TWO of this Essay].
All modern (serial and parallel) general purpose computers are in effect universal Turing machines, but of course their logical design needs not to be identical with the machine just described. What we have done here is to describe the general CONCEPT of a general purpose digital computer, by means of the description of a universal Turing machine.

Go to the HOMEPAGE of this site, so that you can navigate through it, and find my e-mail address.