Derivation of the Crystal Classes II

Derivation of the 32 Crystal Classes (Part Two)

back to homepage

back to Part One

In Part One we started the derivation of the first 27 Crystal Classes. The stereographic projections of the symmetry elements of these Classes and the projections of the face poles of the most general Form of each Class was given in a table. Earlier a matrix (i.e. a general outline) of the entries of this table was given.
We started to derive from the first 10 Classes of this table, columns A and B, which were considered to be already present from the outset, on the basis of our considerations concerning the possible rotational symmetries in Crystals (Part One).
In the ensuing derivations we will call the different Crystal Classes by their entries as given in the matrix and in the table itself.
Until now we have derived (from these 10 Classes) the following Classes :
C2, C4, and C5.
Next we will depict the matrix of the table (of stereographic projections) again, but now with the ten initial Classes and the newly derived Classes in red. Blue entries signify Classes that are still to be derived :

A 1 B 1 C 1 D 1 E 1 F 1 G 1

A 2 B 2 C 2 D 2 E 2 F 2 G 2

A 3 B 3 C 3 D 3 E 3 F 3 G 3

A 4 B 4 C 4 D 4 E 4 F 4 G 4

A 5 B 5 C 5 D 5 E 5 F 5 G 5

The next symmetry element to be added is a 2-fold rotation axis perpendicular to the n-fold axis.
We start again with column A.
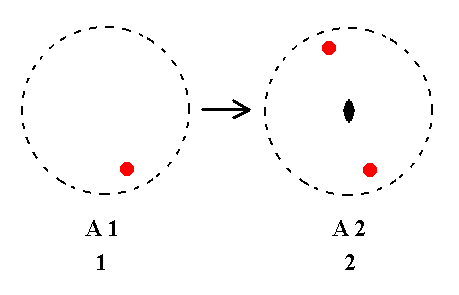
Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to A1 yields A2.
See Figure 1.

Figure 1.
A1---A2

The Class A1 does not have any directionality because the direction of the 1-fold axis is not determined by any crystal face. It can have any direction. When another (than 1-fold) symmetry axis -- in our case a 2-fold rotation axis -- is added we induce a direction, and set the stereogram such that this axis is perpendicular to the plane of the drawing, in accordance with the followed convention for our table.
Nothing new is actually generated in the present case.

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to A2 yields D2.
See Figure 2.

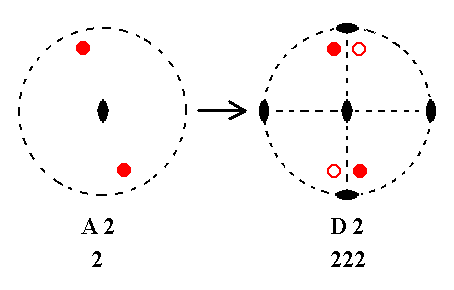Figure 2.
A2---D2

The new 2-fold axis generates, to both initial faces, counter faces by flipping them. The resulting face configuration then implies yet another 2-fold axis, as can be seen from the Figure.

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to A3 yields D3.
See Figure 3.

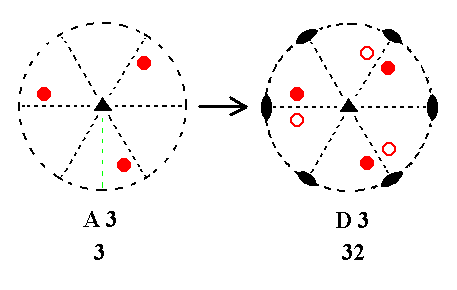Figure 3.
A3---D3

The new 2-fold axis generates to each initial face a counter face by flipping them. The resulting face configuration then implies yet two more 2-fold axes, as can be seen from the Figure.

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to A4 yields D4.
See Figure 4.

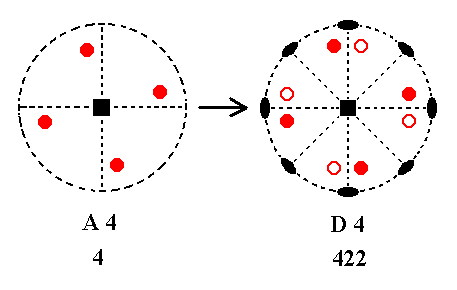Figure 4.
A4---D4

The new 2-fold axis generates to each initial face a counter face by flipping them. The resulting face configuration then implies yet three more 2-fold axes, as can be seen from the Figure.

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to A5 yields D5.
See Figure 5.

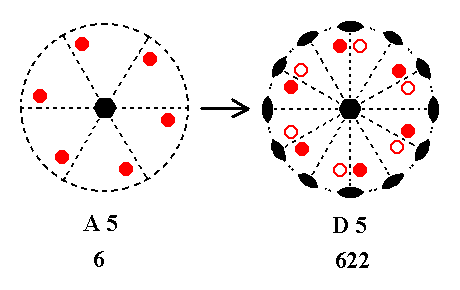Figure 5.
A5---D5

The new 2-fold axis generates to each initial face a counter face by flipping them. The resulting face configuration then implies yet five more 2-fold axes, as can be seen from the Figure ( The right image of this Figure is (drawn) rotated a little bit with respect to the left image, but this is immaterial).

We have now generated from column A four new Classes, D2, D3, D4, and D5, making up column D.
We can summarize our derivations, done so far, in our matrix of table entries :

Next we will add a 2-fold rotation axis perpendicular to the n-fold axis to the Classes in column B :

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to B1 yields C2.
See Figure 6.

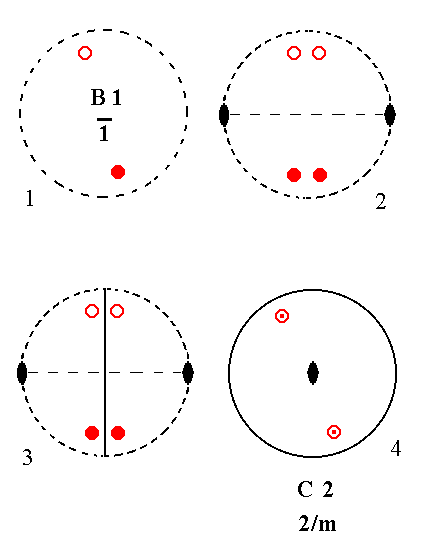Figure 6.
B1---C2
Stages in the derivation of C2 from B1.
(1). Stereogram of the symmetry elements of the Class 1* and of the face poles of the most general Form.
(2). Addition of a 2-fold rotation axis generates two more motifs.
(3). The resulting motif pattern implies a mirror plane. The symmetry now being consistent with 2/m.
(4). In accordance with the adopted convention of our table the stereogram is reoriented as to let the projection plane be perpendicular to the 2-fold axis.

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to B2 yields E2.
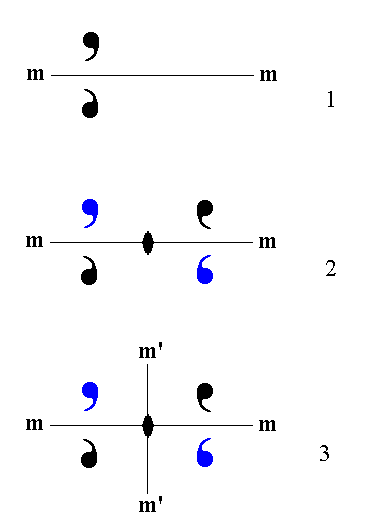The added 2-fold rotation axis generates a second face pair, and implies a new mirror plane containing the 2-fold axis. This new mirror plane is perpendicular to the mirror plane which was already present. See Figures 7 and 8.

Figure 7.
(1). Distribution of motifs consistent with 2* (= m) symmetry (Entry B2).
m signifies the mirror plane. The 2* axis (not drawn) is perpendicular to the mirror plane.
(2). Addition of a 2-fold rotation axis parallel to the mirror plane (which contains that axis) generates two more motifs.
(3). The resulting motif pattern implies a second mirror plane, m'. The symmetry now being consistent with mm2.

The next Figure depicts this in stereographic projection.

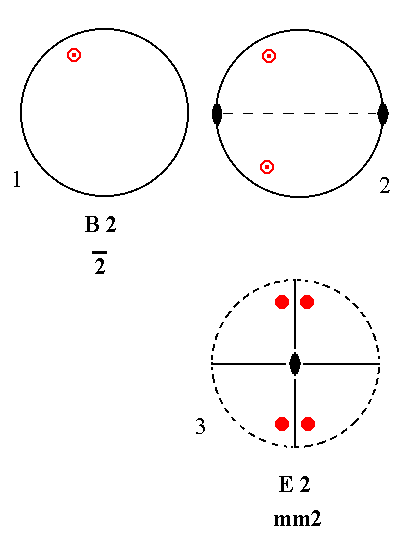Figure 8.
B2---E2
Stages in the derivation of E2 from B2.
(1). Stereogram of the symmetry elements of the Class 2* and of the face poles of the most general Form.
(2). Addition of a 2-fold rotation axis generates two more motifs.
(3). The resulting motif pattern implies a second mirror plane. The symmetry now being consistent with mm2.
In accordance with the adopted convention of our table the stereogram is reoriented as to let the projection plane be perpendicular to the 2-fold axis.

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to B3 yields E3.
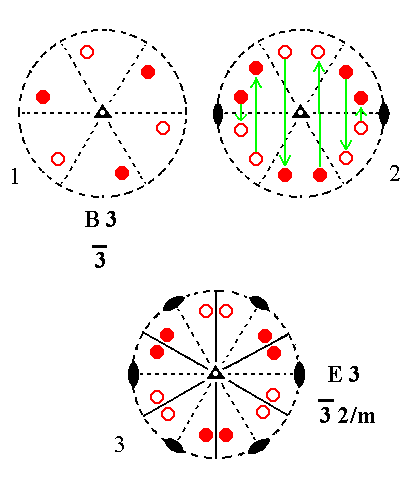See Figure 9. ( The slight rearrangement of the motifs in (3) of this Figure is immaterial since we deal here with a general position of the face poles, implying two degrees of freedom).

Figure 9.
B3---E3
Stages in the derivation of E3 from B3.
(1). Stereogram of the symmetry elements of the Class 3* and of the face poles of the most general Form.
(2). Addition of a 2-fold rotation axis generates six more motifs.
(3). The resulting motif pattern implies three mirror planes and two more 2-fold rotation axes. The symmetry now being consistent with 3*2/m.

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to B4 yields E4.
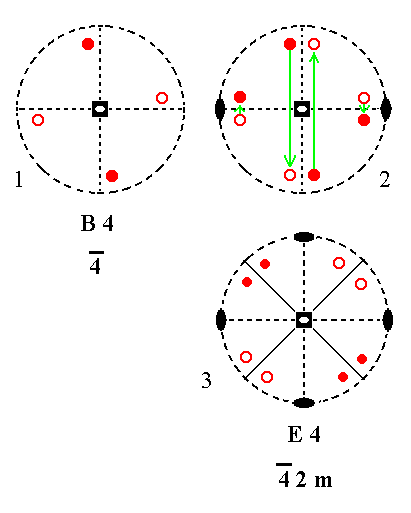Four more motifs are generated by that axis. The resulting motif pattern implies two vertical mirror planes and one more 2-fold rotation axis. See Figure 10 ( The rearrangement of the motifs in (3) of this Figure is immaterial, the stereograms involved being equivalent in so far as they express the symmetry).

Figure 10.
B4---E4
Stages in the derivation of E4 from B4.
(1). Stereogram of the symmetry elements of the Class 4* and of the face poles of the most general Form.
(2). Addition of a 2-fold rotation axis generates four more motifs.
(3). The resulting motif pattern implies two mirror planes and one more 2-fold rotation axis. The symmetry now being consistent with 4*2m.

Addition of a 2-fold rotation axis perpendicular to the n-fold axis, to B5 yields E5.
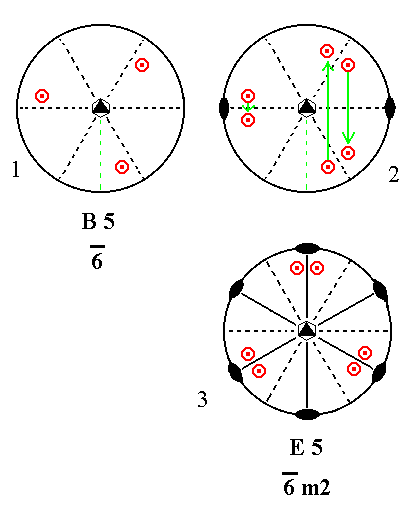Six new motifs are generated. The resulting motif pattern implies three more mirror planes, being vertical, and three 2-fold rotation axes. See Figure 11 ( The motif pattern of (3) of this Figure is (drawn) rotated with respect to that of (2), but this is immaterial, because the position of the motifs with respect to the crystallographic axes remains a general one. So the stereograms involved are equivalent in so far as they express the symmetry).

Figure 11.
B5---E5
Stages in the derivation of E5 from B5.
(1). Stereogram of the symmetry elements of the Class 6* and of the face poles of the most general Form.
(2). Addition of a 2-fold rotation axis generates six more motifs.
(3). The resulting motif pattern implies three vertical mirror planes and three 2-fold rotation axes. The symmetry now being consistent with 6*m2.

Summing up, by adding a 2-fold rotation axis we have generated from the Classes of column B the following new Classes : E2, E3, E4 and E5, i.e. we have generated column E of our table of the (stereograms of the) first 27 Crystal Classes. We will indicate the progress made so far, in the matrix of our table ( The by now derived Crystal Classes are indicated by their respective entries placed in a red background) :

The next symmetry element to be added is a mirror plane parallel to the n-fold axes of the Classes of column A. We will get three new Classes :

Addition of a mirror plane parallel to the n-fold axis of (the Class represented by the entry) A1 yields B2. See Figure 12.

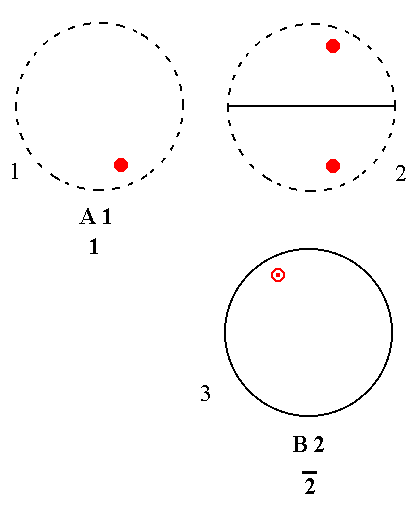Figure 12.
A1---B2
Derivation of B2 from A1.
(1). Stereogram of the symmetry elements of the Class 1 and of the face poles of the most general Form.
(2). Addition of a mirror plane generates a second motif.
(3). Reorientation of the stereogram. The resulting motif pattern is consistent with 2* (= m) symmetry.

Addition of a mirror plane parallel to the n-fold axis of A2 yields E2. See Figure 13.

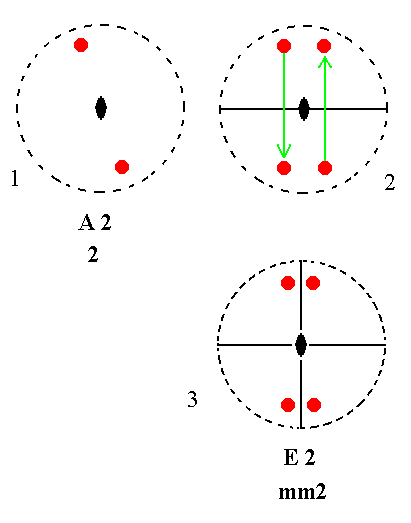Figure 13.
A2---E2
Derivation of E2 from A2.
(1). Stereogram of the symmetry elements of the Class 2 and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates two more motifs.
(3). The resulting motif pattern is consistent with mm2 symmetry.

Addition of a mirror plane parallel to the n-fold axis of A3 yields F3. See Figure 14 ( The motif pattern of (3) of this Figure is (drawn) rotated with respect to that of (2), and also a bit rearranged, but this is immaterial, because the position of the motifs with respect to the crystallographic axes remains a general one. So the stereograms involved are equivalent in so far as they express the symmetry).

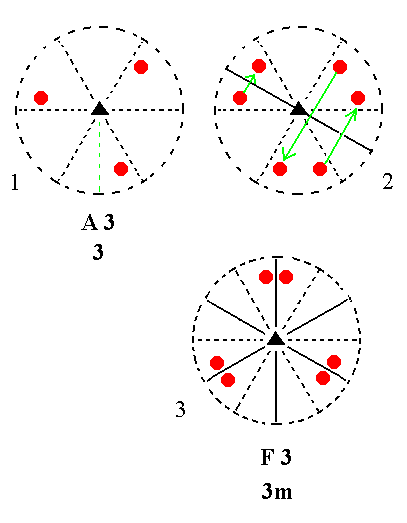Figure 14.
A3---F3
Derivation of F3 from A3.
(1). Stereogram of the symmetry elements of the Class 3 and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates three more motifs.
(3). The resulting motif pattern implies two more vertical mirror planes, and is consistent with 3m symmetry.

Addition of a mirror plane parallel to the n-fold axis of A4 yields F4. See Figure 15.

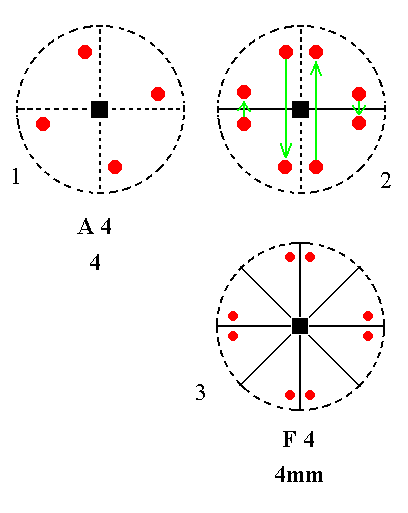Figure 15.
A4---F4
Derivation of F4 from A4.
(1). Stereogram of the symmetry elements of the Class 4 and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates four more motifs.
(3). The resulting motif pattern implies three more vertical mirror planes, and is consistent with 4mm symmetry.

Addition of a mirror plane parallel to the n-fold axis of A5 yields F5. See Figure 16 ( The slight rearrangement of motifs in (3) of this Figure is immaterial because their position is (still) general, so the stereograms involved are equivalent in so far as they express the symmetry).

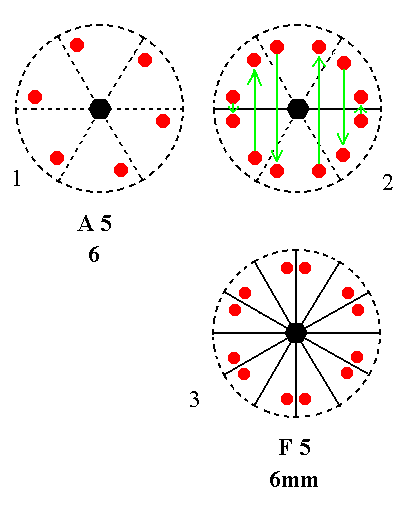Figure 16.
A5---F5
Derivation of F5 from A5.
(1). Stereogram of the symmetry elements of the Class 6 and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates six more motifs.
(3). The resulting motif pattern implies five more vertical mirror planes, and is consistent with 6mm symmetry.

By adding a mirror plane parallel to the n-fold axis of the Classes of column A we have derived three new Classes, namely F3, F4 and F5, i.e. we now have derived all the Classes of column F.
Let us indicate this progress in the matrix of our table of the first 27 Crystal Classes :

Addition of a mirror plane parallel to the n-fold axis of column B does not yield any new Classes :

Addition of a mirror plane parallel to the n-fold axis of (the Class represented by) B1 yields C2.
The Class 1* (= B1) does not have intrinsic directionality imposed by an intrinsic axis. The addition of a mirror plane induces a 2-fold rotation axis, which is now the n-fold rotation axis of the set of motifs. According to the convention of our table the orientation will be such that this 2-fold rotation axis is perpendicular to the projection plane (and thus to the plane of the drawing of the stereogram). See Figure 17.

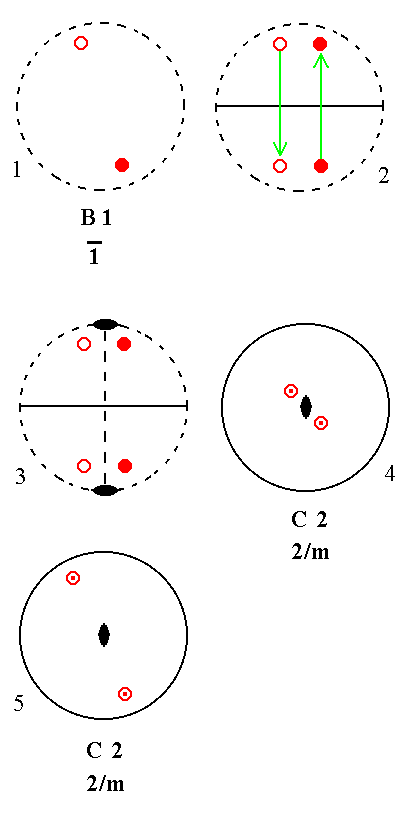Figure 17.
B1---C2
Derivation of C2 from B1.
(1). Stereogram of the symmetry elements of the Class 1* and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates two more motifs.
(3). This addition of the mirror plane and the resulting motif pattern imply a 2-fold rotation axis perpendicular to the added mirror plane, and the motif pattern is now consistent with 2/m symmetry. The resulting stereogram is equivalent to the stereogram of (4), which is obtained by reorienting it.
(4). Stereogram after reorientation of that of (3).
(5). Stereogram with rearranged motifs, causing no change of symmetry.

Addition of a mirror plane parallel to the n-fold axis of B2 yields E2. See Figure 18.

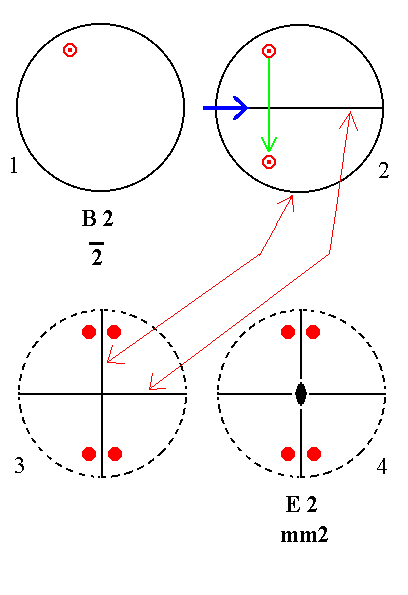Figure 18.
B2---E2
Derivation of E2 from B2.
(1). Stereogram of the symmetry elements of the Class 2* and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates two more motifs.
(3). Reorientation of the stereographic projection, such that the resulting (equivalent) stereogram is as (2) when
' viewed' in the direction of the bold blue arrow. In this reorientation we see again the two mirror planes perpendicular to each other.
(4). The resulting motif pattern implies a 2-fold rotation axis as indicated.

Addition of a mirror plane parallel to the n-fold axis of B3 yields E3.
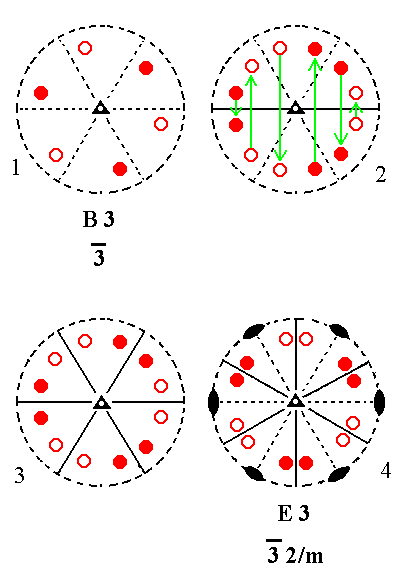See Figure 19 ( The stereogram of (4) of this figure is (drawn) rotated with respect to that of (3), but this is immaterial insofar as symmetry is concerned).

Figure 19.
B3---E3
Derivation of E3 from B3.
(1). Stereogram of the symmetry elements of the Class 3* and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates six more motifs.
(3). The resulting motif pattern implies two more vertical mirror planes.
(4). Also three 2-fold rotation axes are implied. The motif pattern is consistent with 3*2/m symmetry.

Addition of a mirror plane parallel to the n-fold axis of B4 yields E4.
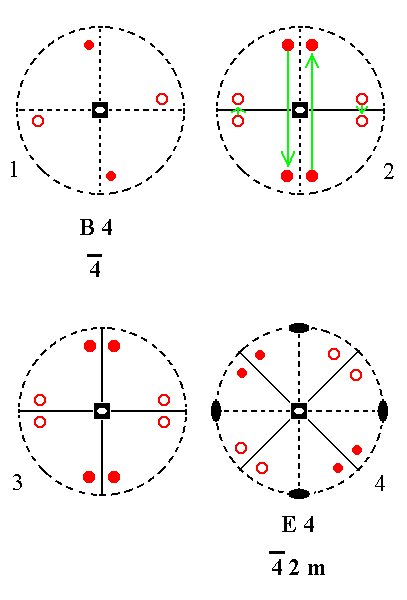See Figure 20 ( The stereogram of (4) is (drawn) rotated with respect to that of (3), but this is immaterial in so far as symmetry is concerned).

Figure 20.
B4---E4
Derivation of E4 from B4.
(1). Stereogram of the symmetry elements of the Class 4* and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates four more motifs.
(3). The resulting motif pattern implies one more vertical mirror plane.
(4). Also two 2-fold rotation axes are implied. The motif pattern is consistent with 4*2m symmetry.

Addition of a mirror plane parallel to the n-fold axis of B5 yields E5.
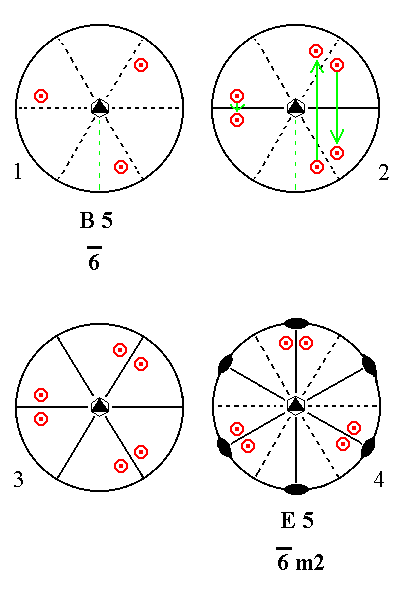See Figure 21 ( The stereogram of (4) of this figure is (drawn) rotated with respect to that of (3), but this is immaterial insofar as symmetry is concerned).

Figure 21.
B5---E5
Derivation of E5 from B5.
(1). Stereogram of the symmetry elements of the Class 6* and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates six more motifs.
(3). The resulting motif pattern implies two more vertical mirror planes.
(4). Also three 2-fold rotation axes are implied. The motif pattern is consistent with 6*m2 symmetry.

So by adding a mirror plane parallel to the n-fold axes of the Classes of column B the following Classes (given by their entries in our table) are generated : C2, E2, E3, E4 and E5.
C2 we had aready generated before, and also all the members of column E were already generated earlier. So no new classes are generated.

The next symmetry element to be added is a mirror plane perpendicular to the n-fold rotation axis.
When we add such a mirror plane to the Classes of columns A and B no new combinations (of symmetry elements) will be generated :

Addition of a mirror plane perpendicular to the n-fold axis of A1 yields B2. The direction of the n-fold axis is not fixed, because it is a 1-fold axis, that can have any direction. See Figure 22.

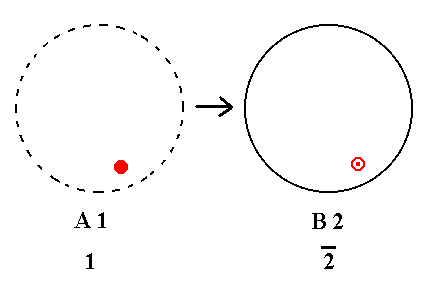Figure 22.
A1---B2

Addition of a mirror plane perpendicular to the n-fold axis of A2 yields C2. See Figure 23.

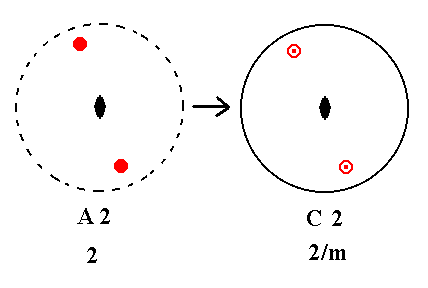Figure 23.
A2---C2

Addition of a mirror plane perpendicular to the n-fold axis of A3 yields B5. See Figure 24.

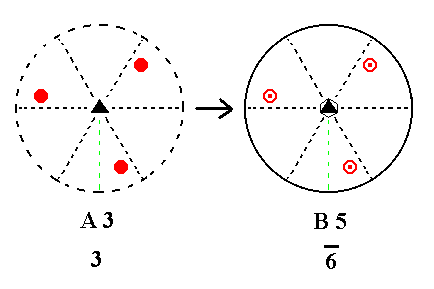Figure 24.
A3---B5

Addition of a mirror plane perpendicular to the n-fold axis of A4 yields C4. See Figure 25.

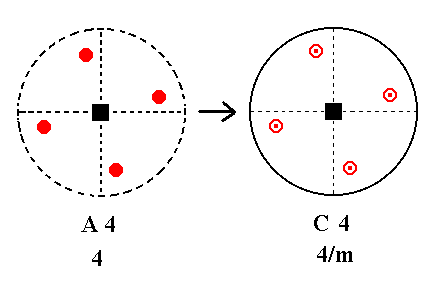Figure 25.
A4---C4

Addition of a mirror plane perpendicular to the n-fold axis of A5 yields C5. See Figure 26.

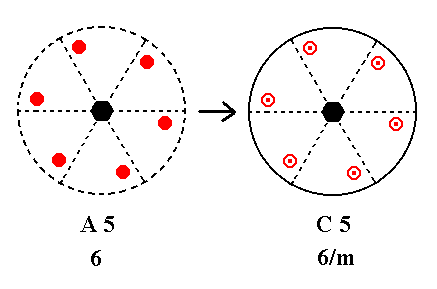Figure 26.
A5---C5

Summing up, addition of a mirror plane perpendicular to the n-fold axes of the Classes of column A yielded the following Classes (as represented by their entries in our table) : B2, C2, B5, C4 and C5.
All these five classes were already derived earlier, so nothing new is generated.

Addition of a mirror plane perpendicular to the n-fold axis of B1 yields C2.
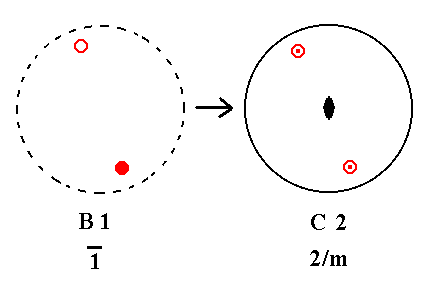B1 only has a center of symmetry. So the direction of the n-fold axis (which is here a 1* axis) is not fixed. Axial direction is finally given by the implied 2-fold rotation axis that comes perpendicular to the added mirror plane. See Figure 27.

Figure 27.
B1---C2
Addition of a mirror plane perpendicular to the initial n-fold axis implies a 2-fold rotation axis that imposes a definite axial direction by being the new n-fold axis.

Addition of a mirror plane perpendicular to the n-fold axis of B2 yields B2.
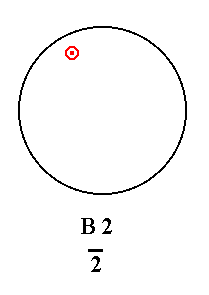The Class represented by B2, namely 2* (= m), has a 2* axis which is perpendicular to the plane of the drawing of our stereogram. Such a 2* axis then already implies a mirror plane perpendicular to it. So nothing changes. See Figure 28.

Figure 28.
B2---B2
Addition of a mirror plane perpendicular to the n-fold axis does not change the Class because that mirror plane was already present.

Addition of a mirror plane perpendicular to the n-fold axis of B3 yields C5. See Figure 29.

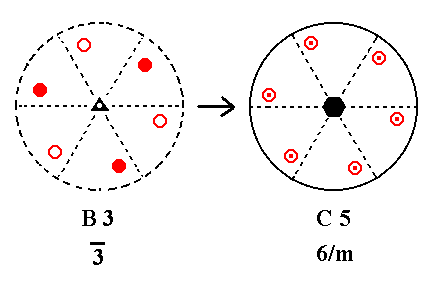Figure 29.
B3---C5

Addition of a mirror plane perpendicular to the n-fold axis of B4 yields C4. See Figure 30.

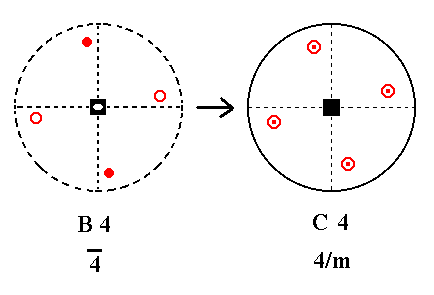Figure 30.
B4---C4

Addition of a mirror plane perpendicular to the n-fold axis of B5 yields B5. See Figure 31.

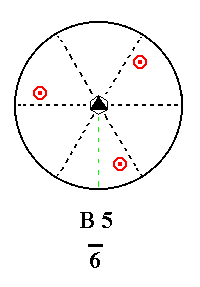Figure 31.
B5---B5
Addition of a mirror plane perpendicular to the n-fold axis does not change the Class because that mirror plane was already present.

Summing up, addition of a mirror plane perpendicular to the n-fold axes of the Classes of column B yielded the following Classes (as represented by their entries in our table) : C2, B2, C5, C4 and B5.
All these five classes were already derived earlier, so nothing new is generated.

Finally we must see what happens when symmetry elements are added to columns C, D, E and F.
If we combine, for example, column C with a 2-fold rotation axis perpendicular to the n-fold axis, then three new classes will be generated, constituting column G :

Adding a 2-fold rotation axis perpendicular to the n-fold axis of C2 (= the first Class in column C) yields G2. Two vertical mirror planes and one more 2-fold rotation axis are implied by the resulting motif pattern. ( The slight displacement of the motifs, as drawn in the stereograms, and the rotation of the drawing are immaterial as far as symmetry is concerned). See Figure 32.

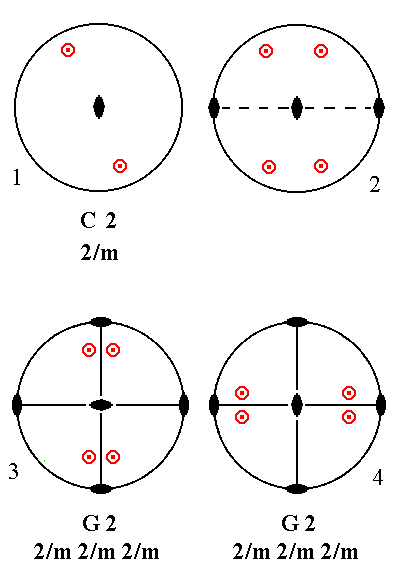Figure 32.
C2---G2
Derivation of G2 from C2.
(1). Stereogram of the symmetry elements of the Class 2/m and of the face poles of the most general Form.
(2). Addition of a 2-fold rotation axis perpendicular to the n-fold axis generates four more motifs.
(3). The resulting motif pattern implies two vertical mirror planes and one more 2-fold rotation axis. The resulting stereogram is equivalent to that of (4).
(4). Rotated stereogram as it is given in the table of the first 27 Classes to be derived.

Adding a 2-fold rotation axis perpendicular to the n-fold axis of C4 (= the second Class in column C) yields G4. See Figure 33.

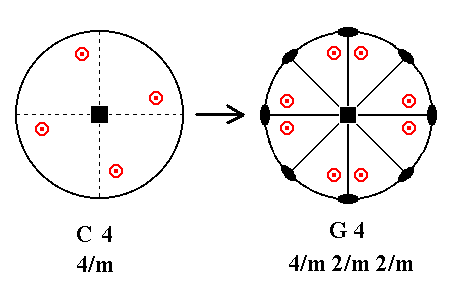Figure 33.
C4---G4
Addition of a 2-fold rotation axis perpendicular to the n-fold axis generates eight new motifs, and implies four vertical mirror planes and three more 2-fold rotation axes.

Adding a 2-fold rotation axis perpendicular to the n-fold axis of C5 yields G5. See Figure 34 ( The motifs are (drawn) a little reshuffled, but their positions remain general, and so still reflect the effect of the generated new symmetry).

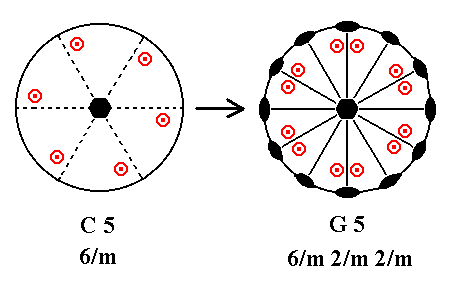Figure 34.
C5---G5
Addition of a 2-fold rotation axis perpendicular to the n-fold axis generates 12 new motifs, and implies six vertical mirror planes and five more 2-fold rotation axes.

Summarizing : By adding a 2-fold rotation axis perpendicular to the n-fold axis of the Classes of column C yielded the following new Classes : G2, G4 and G5, i.e. all the Classes of column G. Let us indicate this result in the matrix of entries of our table of the first 27 Crystal Classes :

We see that we now have derived all the Crystal Classes listed in our table. Of course this table was already presupposed from the beginning, so we must check if, or if not, the table is in fact bigger, i.e. we must check whether the addition of the above mentioned symmetry elements to Classes having at most one more-than-2-fold axis -- (an addition) such that this one more-than-2-fold axis will not be multiplied -- will now have generated all the Classes with at most one more-than-2-fold axis.

So we must still add those symmetry elements to the Classes of the columns C, D, E, F and G.
For column C we have done so already with respect to the addition of a 2-fold rotation axis perpendicular to the n-fold axis.

The Classes of column C all have already a center of symmetry, so the addition of that symmetry element cannot have any effect. Let's explain this. See Figures 34a and b.

As an example we take the first Class of column C, i.e. Class C2, and show that it already has a center of symmetry.

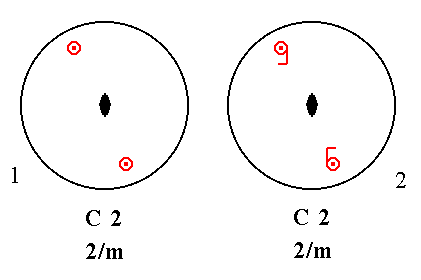Figure 34a.
(1). Stereogram of the Class C2.
(2). Invocation of real motifs (represented by comma's) at the locations of the (projections of the) face poles.

In the next Figure (continuing the explanation that the Classes of column C already possess a center of symmetry) we depict the configuration of Figure 34a, such that our direction of view is perpendicular to that of Figure 34a.

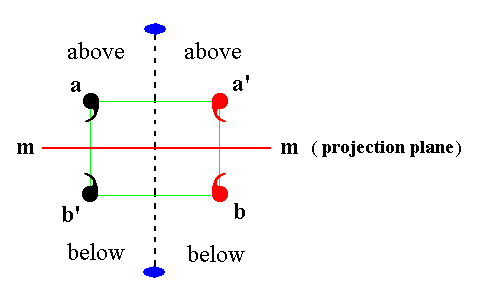
Figure 34b.
Four motifs related to each other by a 2-fold rotation and a reflection.
In this drawing we should imagine that a comma also differs in the direction of viewing, indicated by the coloring : If a comma with its black side toward the beholder is rotated by 180⁰ about the axis indicated by the small blue solid ellipses (This axis thus lies in the plane of the drawing), then it will show its red side. So there is no mirror plane perpendicular to the projection plane and containing that 2-fold axis.
We can clearly see that motif b is the inverted image of motif a (and vice versa), and that motif b' is the inverted image of motif a' (and vice versa), because every detail of the comma, including the color, is interchanged. And that is precisely what happens when the motifs are related to each other by the operation of inversion (with the intersection of the 2-fold axis with the projection plane as inversion point). Then the whole motif configuration indeed possesses a center of symmetry (About a center of symmetry see also Figure 3 in Part One, and Figure 38b in the present Part).

The same reasoning applies to the other two Classes of column C.

Addition of a mirror plane perpendicular to the n-fold axis of the Classes of column C also cannot have any effect because these Classes already have such a mirror plane.

Addition of a mirror plane parallel to the n-fold axis of the Classes of column C will yield the same Classes as did the addition of a 2-fold rotation axis perpendicular to the n-fold axis :

Addition of a mirror plane parallel to the n-fold axis of C2 yields G2. See Figure 35 ( The displacements of motifs as drawn in this Figure are immaterial insofar symmetry is concerned).

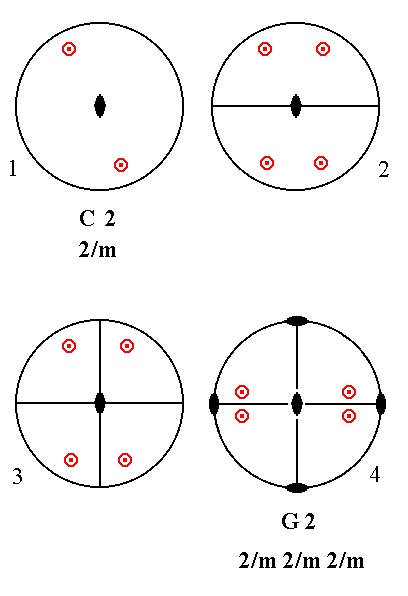Figure 35.
C2---G2
Derivation of G2 from C2.
(1). Stereogram of the symmetry elements of the Class 2/m and of the face poles of the most general Form.
(2). Addition of a mirror plane parallel to the n-fold axis generates four more motifs.
(3). The resulting motif pattern implies one more vertical mirror plane and two more 2-fold rotation axes (indicated in (4)).
(4). Rotated stereogram, with the implied 2-fold rotation axes indicated, as it was given in the table of the first 27 Classes to be derived.

In (3) of the above Figure we stated that "the resulting motif pattern implies one more vertical mirror plane and two more 2-fold rotation axes". Although that is true, it is not evident just like that.
In the Remark (Inframe) in Part Four, below Figure 1 there, the implication of mirror planes and 2-fold axes is explained. There, in Figure 1a (lower part of that Figure) we can see that if we have a mirror plane (= the added mirror plane) and also a mirror plane perpendicular to it (coinciding with the projection plane), then a 2-fold rotation axis, lying in the projection plane, is implied. And if we have a mirror plane (= the added mirror plane) and a 2-fold axis (= the (vertical) n-fold axis) lying in that mirror plane, then another mirror plane, perpendicular to the first, and containing that 2-fold axis, is implied, and then also another 2-fold axis contained in the implied mirror plane, is implied.
For easy reference we here reproduce Figure 1a of the mentioned Remark. The lower part of the Figure is especially relevant :

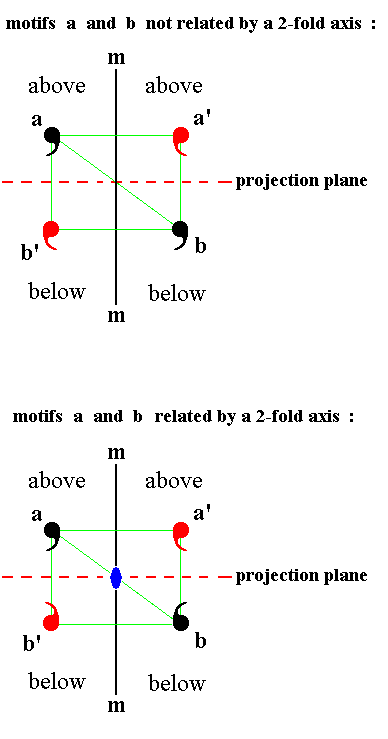
Figure 35a. Figure 1a from Remark (inframe) in Part Four.

Addition of a mirror plane parallel to the n-fold axis of C4 yields G4. See Figure 36.

Figure 36.
C4---G4
Addition of a mirror plane parallel to the n-fold axis generates eight new motifs, and implies three more vertical mirror planes and four 2-fold rotation axes.

This needs to be further explained.
Because of the action of the added mirror plane we now have four sets of motifs (each set containing four motifs, two upper and two lower ones). These four sets must comply with the vertical 4-fold axis such that they are congruent with respect to each other, i.e. they are repeated every 90⁰ when rotated about the vertical axis. A second vertical mirror plane, perpendicular to the added mirror plane, is implied by the vertical 4-fold axis.
So what we have up to now is the following :

Figure 36a.

Two more vertical mirror planes are implied as follows :

Figure 36b.

Motif pair a is symmetric to motif pair b with respect to the mirror plane lying between them. The pairs a and b, and their mirror plane, are repeated, yielding the pair c and d with a mirror plane between them. Let's depict this situation using motifs (represented by comma's) instead of (projections of) face poles :

Figure 36c.

In the above Figure we clearly see that the configuration is symmetric with respect to the line (representing a plane) m. So a mirror plane is implied. This mirror plane is then duplicated by the mirror plane between a and b resulting in yet another mirror plane.
In Figure 35a (lower part) we can see that when we have two mirror planes perpendicular to each other, then a 2-fold rotation axis is implied lying in both planes (namely in their line of intersection). This means that all the vertical mirror planes -- being perpendicular to the projection plane which is in our case also a (horizontal) mirror plane -- must contain a 2-fold rotation axis also contained in the projection plane. This, finally gives us the symmetry configuration of G4 (Figure 36).

Addition of a mirror plane parallel to the n-fold axis of C5 yields G5. See Figure 37.

Figure 37.
C5---G5
Addition of a mirror plane parallel to the n-fold axis generates 12 new motifs, and implies five more vertical mirror planes and six 2-fold rotation axes.

The explanation of this derivation is analogous to the one given above.

So by adding a mirror plane parallel to the n-fold axis of the Classes of column C yields column G :
G2, G4 and G5. Indeed nothing new is generated.

Now we must check whether or not still new Classes appear when we add the mentioned symmetry elements (center of symmetry, a 2-fold rotation axis perpendicular to the n-fold axis, a mirror plane parallel to the n-fold axis, and a mirror plane perpendicular to that axis) to the (Classes in the) columns D, E, F and G.
Let's start to add a center of symmetry to the Classes of these columns :

Addition of a center of symmetry to (the Class represented by) D2 yields G2.
For a motif pattern to possess a center of symmetry it is demanded that for each motif there must exist (in that same motif pattern) a parallel counter motif lying exactly opposite to it. If we meet this demand in the stereogram of D2 we get the motif pattern of G2 where at the same time a horizontal and two vertical mirror planes are implied. See Figure 38.

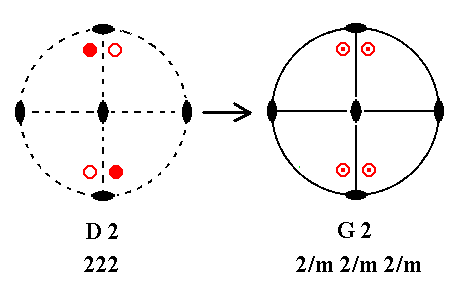Figure 38.
D2---G2
Addition of a center of symmetry generates four new motifs, and implies a horizontal and two vertical mirror planes.

Let's explain this.
The next Figure uses motifs (represented by comma's) there where we normally indicate the location of projected face poles (by means of small solid or open circles).

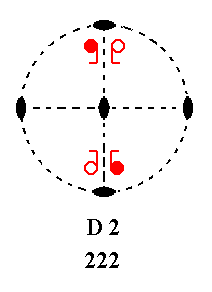Figure 38a.
Motifs, represented by comma's. Solid comma's correspond to upper face poles, open comma's to lower face poles. One can easily see the action of the 2-fold rotation axes on the motifs.

Addition of a center of symmetry generates for each motif a counter motif. See the next Figure.

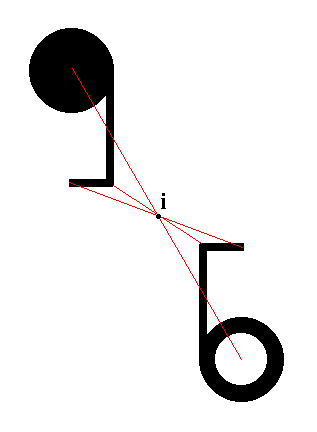Figure 38b.
Two motifs related by a center of symmetry (i). This means that the whole pattern has a center of symmetry : it will be mapped onto itself by the operation of inversion in the point i.
When one motif is subjected to inversion left and right will be interchanged as well as top and bottom, and back and belly.
One motif is drawn as a solid comma, the other as an open comma, where solid and open stand for the fact that one motif is lying above the projection plane, and the other is lying below it, while they are at the same time turned upside down with respect to each other.

The next Figure shows that when a center of symmetry is added (going to lie at the center of the projection plane) each motif sends an inversed copy of itself right to the opposite side of the point of inversion.

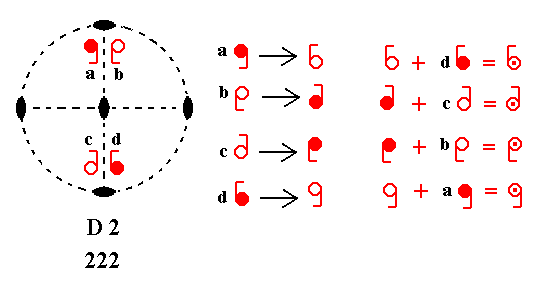
Figure 38c.
Upper motif a sends an inverted copy to the location right below (with respect to the projection plane, which is the plane of the drawing) the upper motif d.
Lower motif b sends an inverted copy to the location right above the lower motif c.
Lower motif c sends an inverted copy to the location right above lower motif b.
Upper motif d sends an inverted copy to the location right below upper motif a.
So in each of the four locations a, b, c, d we will see two motifs right above each other, and symmetrical with respect to the projection plane.

The resulting motif configuration is depicted in the next Figure.

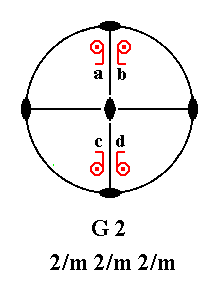Figure 38d.
Motifs, represented by comma's. A comma, centered with a point, signifies two motifs, one right below the other, and related by a reflection in the projection plane.
We can clearly see that one horizontal mirror plane and two vertical mirror planes are now implied.
The symmetry configuration is that of G2.

Addition of a center of symmetry to D3 yields E3.
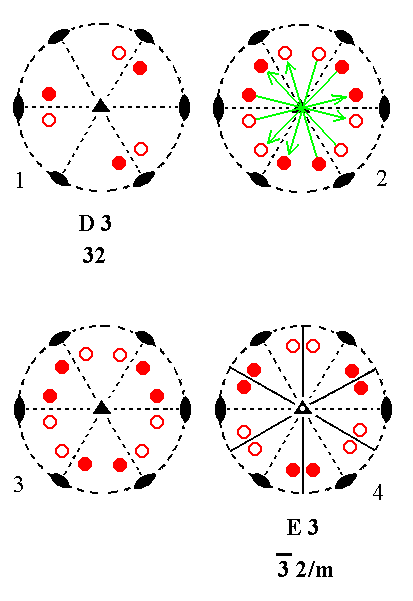Again, each motif should have a counter motif exactly opposite to it. See Figure 39 ( The motifs in (4) are (drawn) a bit reshuffled with respect to those of (3), but this is immaterial as far as symmetry is concerned).

Figure 39.
D3---E3
Derivation of E3 from D3.
(1). Stereogram of the symmetry elements of the Class 32 and of the face poles of the most general Form.
(2). Addition of a center of symmetry generates six more motifs.
(3). The resulting motif pattern.
(4). The new motif pattern implies three vertical mirror planes, and is consistent with 3*2/m symmetry.

The next Figures explain this.

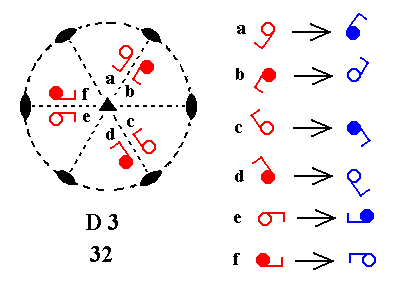
Figure 39a.
In the stereogram of D3 motifs are placed at the locations of the (projections of the) face poles. When a center of symmetry is added each motif sends an inverted copy of itself to the opposite side of the center of the projection plane. The inversion of the motifs a, b, c, d, e, f is indicated on the right side of the Figure.

The resulting motif configuration is depicted in the next Figure.

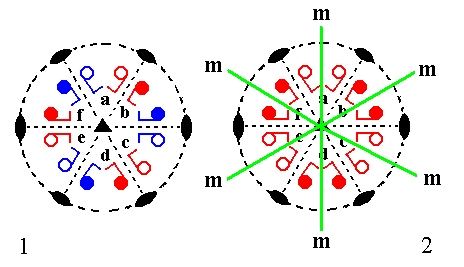
Figure 39b.
The inverted motifs are put in place, resulting in each motif now having a counter part that results from its inversion in (through) the projection plane's central point. The motif pattern now clearly implies three vertical mirror planes, but no horizontal mirror plane. The symmetry configuration is that of E3.

Addition of a center of symmetry to D4 yields G4. See Figure 40.

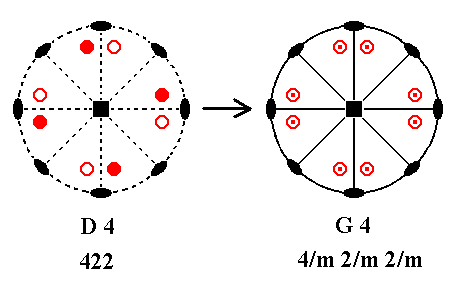Figure 40.
D4---G4
Addition of a center of symmetry generates eight new motifs, and implies a horizontal and four vertical mirror planes.

Addition of a center of symmetry to D5 yields G5. See Figure 41.

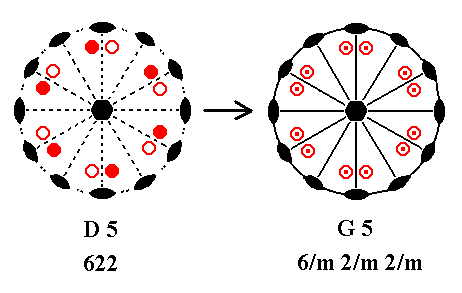Figure 41.
D5---G5
Addition of a center of symmetry generates twelve new motifs, and implies a horizontal and six vertical mirror planes.

Summarizing : By adding a center of symmetry to the Classes of column D we obtained G2, E3, G4 and G5. So nothing new is generated.
In Part Three we will continue this search, by adding a center of symmetry to the Classes of column E, etc.

To continue, click HERE for Part Three.

back to homepage

back to Part One

****************

A 1	B 1	C 1	D 1	E 1	F 1	G 1
A 2	B 2	C 2	D 2	E 2	F 2	G 2
A 3	B 3	C 3	D 3	E 3	F 3	G 3
A 4	B 4	C 4	D 4	E 4	F 4	G 4
A 5	B 5	C 5	D 5	E 5	F 5	G 5