Continuing the investigation of Part Three, we're now going to check whether or not the addition of a mirror plane parallel to the (vertical) n-fold axis, to the symmetry content of the Crystal Classes of the columns D, E, F and G of our table of the first 27 Crystal Classes, will generate new Classes, i.e. Classes, different from the 27 Classes already derived possessing at most one more-than-2-fold axis.
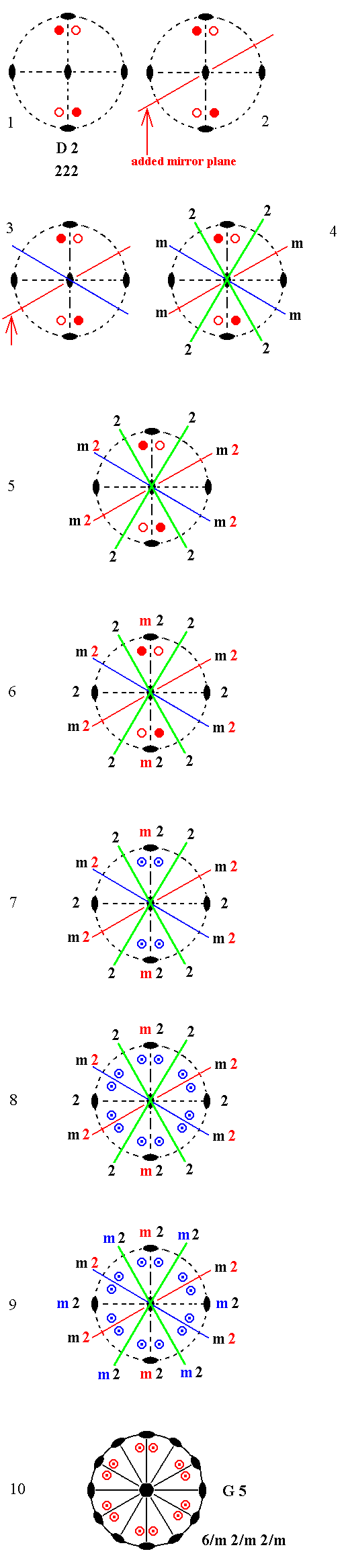
Addition of a mirror plane parallel to the (vertical) n-fold axis of the Class represented by the entry D2 (= the first Class of column D) and making angles of 300 and 600 with existing 2-fold axes yields G5. See Figure 1.

Figure 1. Derivation of G5 from D2.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 222 represented by the entry D2.
(2). Addition of a mirror plane parallel to the (vertical) n-fold axis of D2 and making angles of 300 and 600 with existing 2-fold axes.
(3). The action of the existing horizontal 2-fold axes generates a second mirror plane.
(4). Each mirror plane generates a new 2-fold axis (green) by reflection of an existing one.
( A 2-fold rotation axis is indicated by its conventional graphic symbol or by the
symbol 2, while a mirror plane is indicated by the symbol m ).
(5). The new 2-fold axes duplicate existing 2-fold axes, resulting in new 2-fold axes contained in the mirror planes ( This fact is indicated by the symbol m2 ).
(6). The 2-fold axes, indicated in green, duplicate a mirror plane resulting in yet another mirror plane containing one of the horizontal 2-fold axes originally present (the one that is vertically drawn in the stereogram).
(7). The motifs now must comply with the fact that they should be related to each other by a mirror plane (the one vertically drawn in the stereogram). This means that four new motifs are generated as indicated.
(8). The symmetry elements, now present, multiply the motifs resulting in a pattern as indicated.
(9). This motif pattern demands the presence of two more vertical mirror planes containing the 2-fold axes that had been indicated by the color green.
One of the originally existing 2-fold axes came to be contained in a
mirror plane earlier ((6)). Now the motif pattern demands yet another mirror plane containing the other horizontal 2-fold axis which was originally present (horizontally drawn in the stereogram).
So we now have six sets, each consisting of a vertical mirror plane containing a horizontal 2-fold axis.
A horizontal mirror plane is implied by the configuration of the motifs (i.e. the presence of lower motifs precisely below corresponding upper motifs) and by (i.e. combined with) their relation to the 2-fold axes ( See for further explanation concerning the question when mirror planes are implied and when they are not, the Remark (Inframe) directly below).
The resulting symmetry configuration is that of G5.
(10). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 6/m 2/m 2/m represented by the entry G5.
Remark (Inframe, including several Figures) :
Addition of a mirror plane parallel to the n-fold axis of D2 and making angles of 450 with existing 2-fold axes yields E4. See Figure 2.
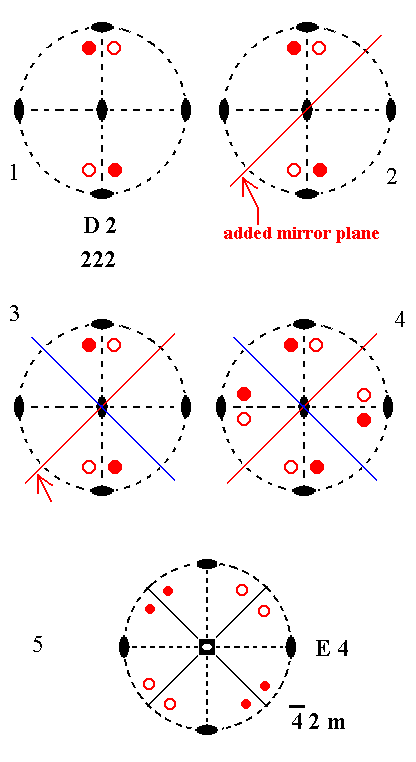
Figure 2. Derivation of E4 from D2.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 222 represented by the entry D2.
(2). Addition of a mirror plane parallel to the n-fold axis of D2 and making angles of 450 with existing 2-fold axes.
(3). The horizontal 2-fold axes generate a second mirror plane.
(4). The mirror planes generate four more motifs as indicated. The resulting motif pattern demands that the n-fold axis, which was originally a 2-fold rotation axis, becomes a 4-fold roto-inversion axis (See (5)). The final symmetry configuration is that of E4.
(5). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 4*2m represented by the entry E4 (In this stereogram the motifs are (drawn) redistributed with respect to (4), but insofar the symmetry is concerned they show the same pattern, and their positions are still general).
Addition of a mirror plane parallel to the n-fold axis of D2 and making an angle of 900 with one of the existing 2-fold axes, yields G2. See Figure 3.
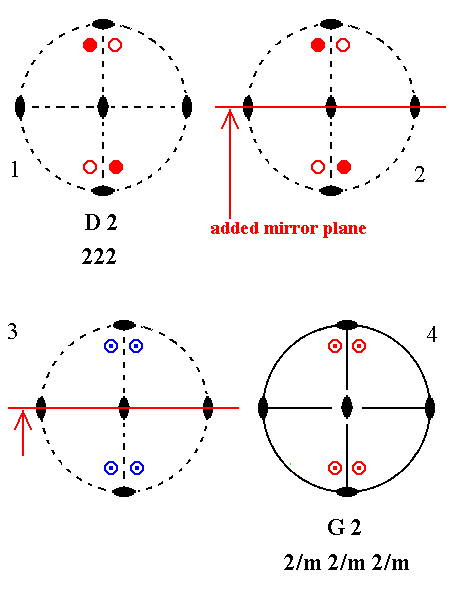
Figure 3. Derivation of G2 from D2.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 222 represented by the entry D2.
(2). Addition of a mirror plane parallel to the n-fold axis and making an angle of 900 with one of the existing 2-fold axes.
(3). The added mirror plane generates four more motifs as indicated. The resulting motif pattern demands one more vertical mirror plane, and a horizontal mirror plane (See (4)). For an explanation about when and how a mirror plane is implied, see the Remark (inframe) above.
The symmetry configuration is now that of G2.
(4). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 2/m 2/m 2/m represented by the entry G2.
Addition of a mirror plane parallel to the n-fold axis of D3 and making angles of 300 and 900 with existing 2-fold axes, yields E3. See Figure 4.
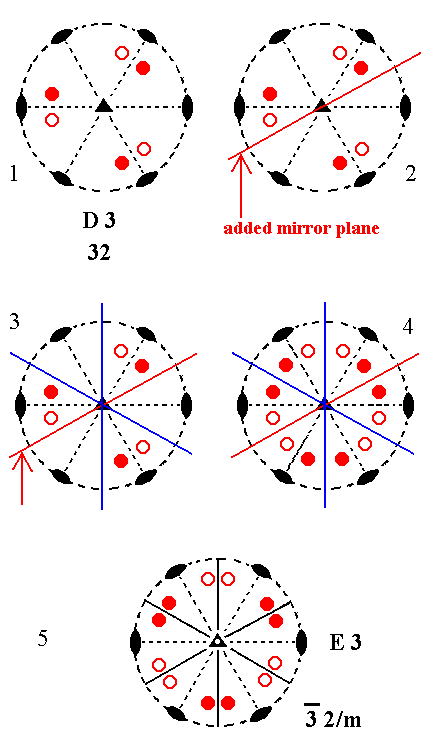
Figure 4. Derivation of E3 from D3.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 32 represented by the entry D3.
(2). Addition of a mirror plane parallel to the n-fold axis of D3 and making angles of 300 and 900 with existing 2-fold axes.
(3). The existing 2-fold axes generate two more mirror planes.
(4). The mirror planes, now present, generate six more motifs as indicated. The resulting motif pattern demands that the (vertical) n-fold axis, which originally was a 2-fold axis, becomes a 3-fold roto-inversion axis (See (5).
(5). The resulting symmetry configuration is that of E3.
If we add a mirror plane (parallel to the n-fold axis) to the symmetry content of D3 and making an angle of 450 with an existing 2-fold axis, then an angle of 150 will be involved, leading to a symmetry forbidden for crystals.
Addition of a mirror plane parallel to the n-fold axis of D3 and making angles of 600 with existing 2-fold axes yields E5. See Figure 5.
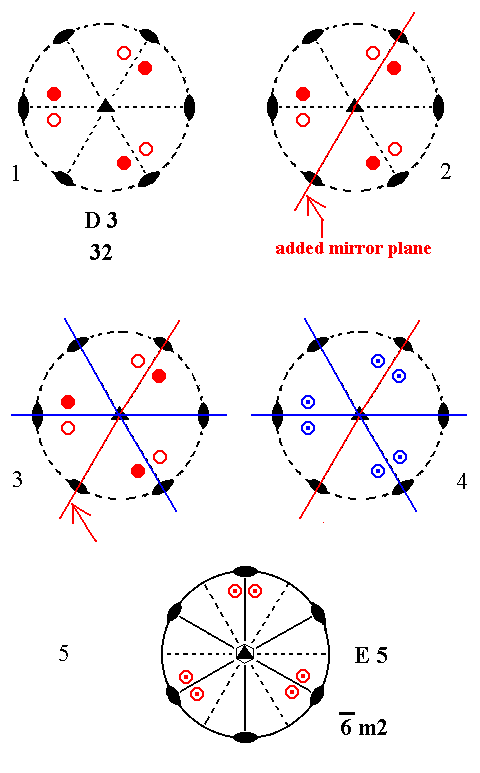
Figure 5. Derivation of E5 from D3.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 32 represented by the entry D3.
(2). Addition of a mirror plane parallel to the n-fold axis of D3 and making angles of 600 with existing 2-fold axes.
(3). The existing 2-fold axes generate two more mirror planes.
(4). The mirror planes generate six more motifs as indicated.
(5). The resulting motif pattern demands a horizontal mirror plane ( See for an explanation about when and how a horizontal mirror plane is implied, the Remark (inframe) above ). It also demands that the (vertical) n-fold axis, which was originally a 3-fold rotation axis, becomes a 6-fold roto-inversion axis. The resulting symmetry configuration is that of E5.
Addition of a mirror plane parallel to the n-fold axis of D4 and making angles of 450 and 900 with existing 2-fold axes, yields G4. See Figure 6.
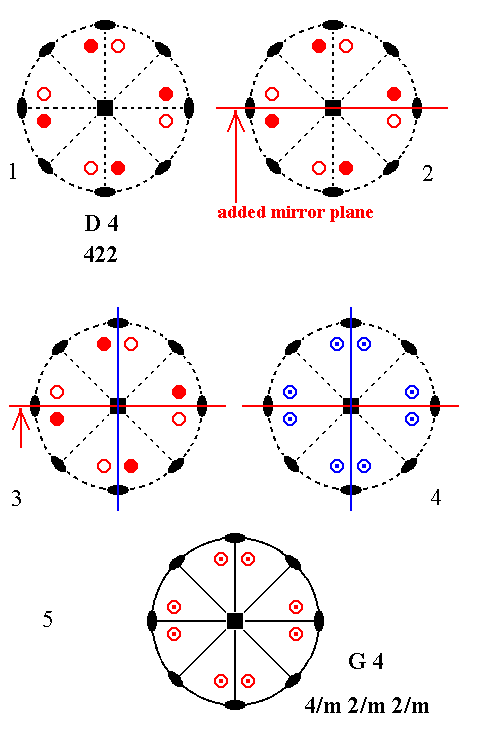
Figure 6. Derivation of G4 from D4.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form of the Class 422 represented by the entry D4.
(2). Addition of a mirror plane parallel to the n-fold axis of D4 and making angles of 450 and 900 with existing 2-fold axes.
(3). An existing 2-fold axis generates a second mirror plane.
(4). The mirror planes generate eight new motifs as indicated.
(5). The resulting motif pattern demands a horizontal mirror plane ( See for explanation the Remark (inframe) above ), and two more vertical mirror planes. The resulting symmetry configuration is that of G4.
Angles of 300 and 600 imply angles of 150 leading to forbidden symmetry.
Addition of a mirror plane parallel to the n-fold axis of D5 and making angles of 300, 600 and 900 with existing 2-fold axes, yields G5. See Figure 7.
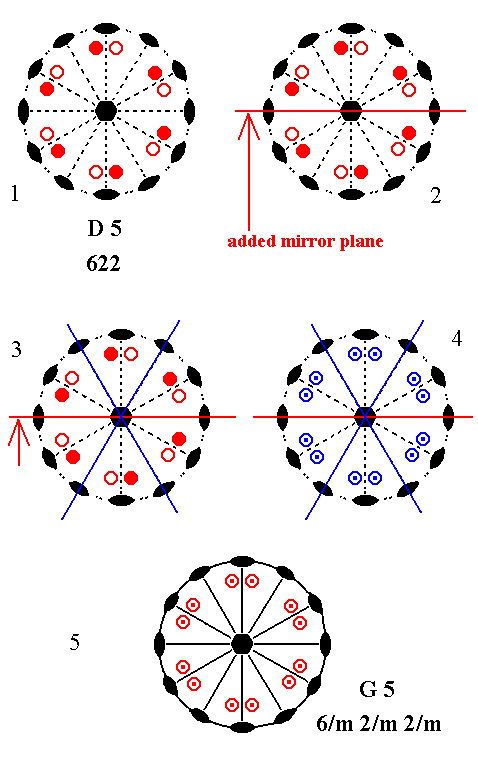
Figure 7. Derivation of G5 from D5.
(1). Stereogram of the symmetry elements and of the face poles of te most general Form, of the Class 622 represented by the entry D5.
(2). Addition of a mirror plane parallel to the n-fold axis of D5 and making angles of 300, 600 and 900 with existing 2-fold axes.
(3). The added mirror plane is duplicated by an existing 2-fold axis, and the resulting second mirror plane is again duplicated by another existing 2-fold axis.
(4). The mirror planes generate 12 new motifs as indicated.
(5). The resulting motif pattern demands one horizontal mirror plane and three more vertical mirror planes. ( See for the explanation of the implication of mirror planes the Remark (inframe) above ). The resulting symmetry configuration is that of G5.
We continue with the addition of a mirror plane parallel to the n-fold axis of D5.
Summing up : Addition of a mirror plane parallel to the (vertical) n-fold axis of the Classes of column D generated the following Classes : G5, E4, G2, E3, E5 and G4.
Next we will investigate the addition of a mirror plane parallel to the (vertical) n-fold axis of the Classes of column E.
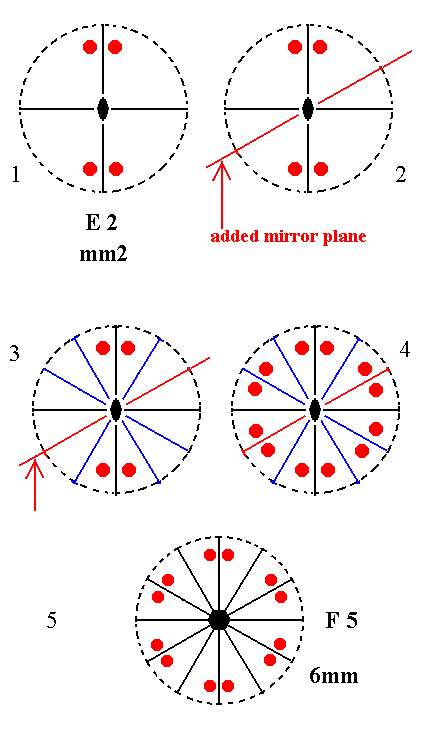
Figure 8. Derivation of F5 from E2.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class mm2 represented by the entry E2.
(2). Addition of a mirror plane parallel to the n-fold axis of the Class represented by the entry E2 and making angles of 300 and 600 with existing vertical mirror planes.
(3). The added mirror plane, together with the existing mirror planes generates three more vertical mirror planes.
(4). All these mirror planes generate eight more motifs.
(5). The resulting motif configuration demands that the (vertical) n-fold axis, which originally was a 2-fold rotation axis, becomes a 6-fold rotation axis. The symmetry configuration is now that of F5.
Addition of a mirror plane parallel to the n-fold axis of E2 and making angles of 450 with existing mirror planes, yields F4. See Figure 9.
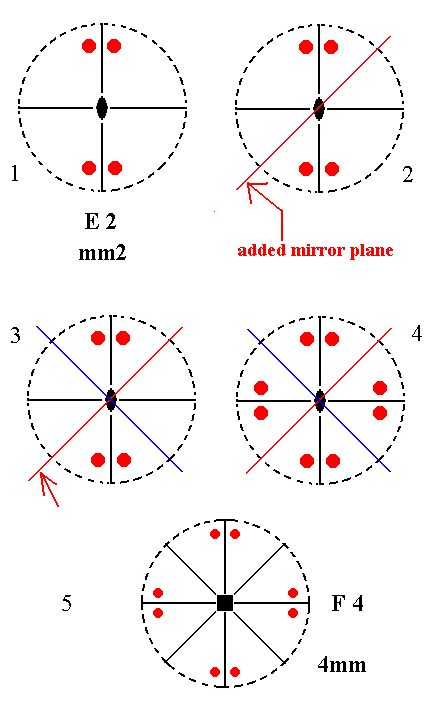
Figure 9. Derivation of F4 from E2.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class mm2 represented by the entry E2.
(2). Addition of a mirror plane parallel to the n-fold axis of E2 and making angles of 450 with existing mirror planes.
(3). A second mirror plane is generated.
(4). The mirror planes generate four more motifs.
(5). The resulting motif pattern now implies a 4-fold vertical rotation axis. The symmetry configuration is that of F4.
A mirror plane 900 apart from another mirror plane is already present in the symmetry configurarion of E2.
Addition of a mirror plane parallel to the n-fold axis of E3 can only be such that it contains one of the existing horizontal 2-fold axes. In all other cases it either coincides with an already existing mirror plane (and then, of course nothing is added at all), or an angle smaller then 300 will be involved, leading to a forbidden symmetry.
Addition of a mirror plane parallel to the n-fold axis of E3 and coinciding with one of the horizontal 2-fold axes yields G5. See Figure 10.
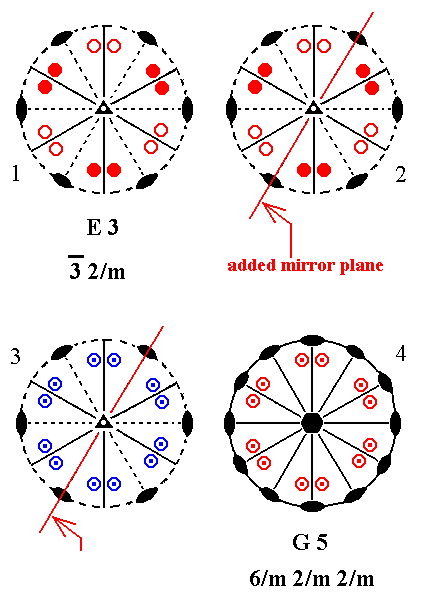
Figure 10. Derivation of G5 from E3.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 3*2/m represented by the entry E3.
(2). Addition of a mirror plane parallel to the n-fold axis and coinciding with one of the horizontal 2-fold rotation axes.
(3). The added mirror plane generates 12 new motifs as indicated.
(4). The resulting motif pattern demands a horizontal mirror plane, and three more horizontal 2-fold rotation axes. The vertical mirror planes, now present, generate two more vertical mirror planes. The (vertical) n-fold axis, which was originally a 3-fold roto-inversion axis, becomes a 6-fold rotation axis. The symmetry configuration is that of G5.
Addition of a mirror plane parallel to the n-fold axis of E4 can only be such that it coincides with an existing horizontal 2-fold axis, otherwise it would either coincide with an already existing mirror plane, or involve an angle of 150 -- implied when an angle of 300 or 600 is taken -- leading to a forbidden symmetry.
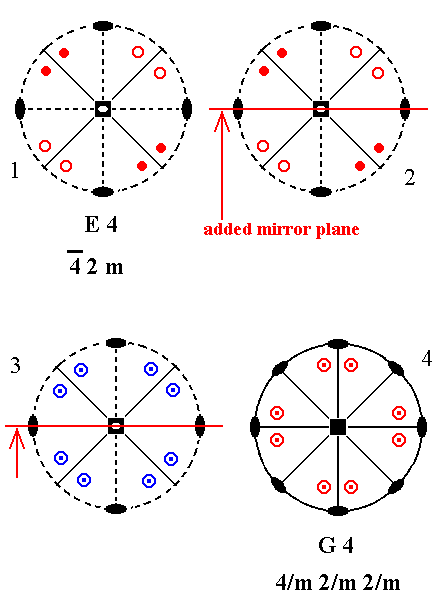
Figure 11. Derivation of G4 from E4.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 4*2m represented by the entry E4.
(2). Addition of a mirror plane parallel to the n-fold axis of E4 and coinciding with an existing horizontal 2-fold rotation axis.
(3). The added mirror plane generates eight new motifs.
(4). The resulting motif pattern implies a horizontal mirror plane and two more horizontal 2-fold rotation axes. The originally existing mirror planes duplicate the added mirror plane. The motif pattern also demands that the (vertical) n-fold axis, which originally was a 4-fold roto-inversion axis, becomes a 4-fold rotation axis. The symmetry configuration is that of G4 ( The fact that the motifs of (4) are drawn rotated with respect to those of (3) is immaterial insofar symmetry is concerned).
Addition of a mirror plane parallel to the n-fold axis of E5 can only be such that it bisects the angle between existing mirror planes, otherwise it either coincides with an already existing mirror plane, or involves an angle of 150 -- which will be implied when an angle of 450 is taken -- leading to a forbidden symmetry.
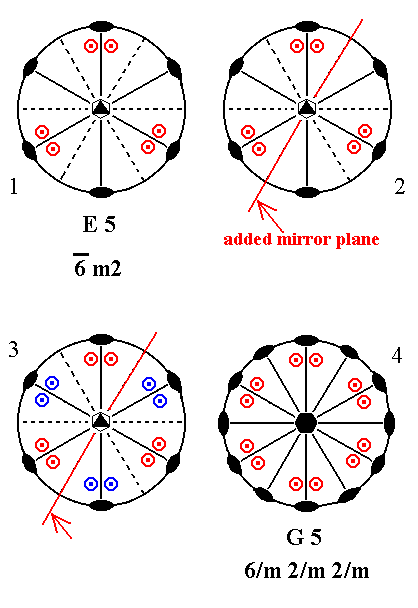
Figure 12. Derivation of G5 from E5.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 6*m2 represented by the entry E5.
(2). Addition of a mirror plane parallel to the n-fold axis of E5 and bisecting the angle between existing mirror planes.
(3). The added mirror plane generates 12 new motifs as indicated.
(4). The resulting motif pattern implies three more horizontal 2-fold axes. It also demands that the (vertical) n-fold axis, which was originally a 6-fold roto-inversion axis, becomes a 6-fold rotation axis. The mirror planes, now present, generate two more vertical mirror planes.
The symmetry configuration is that of G5.
Summing up : Addition of a mirror plane parallel to the n-fold axis of the Classes of column E generated the following Classes : F5, F4, G5 and G4.
Next we will investigate the addition of a mirror plane parallel to the n-fold axis of the Classes of column F.
Addition of a mirror plane parallel to the n-fold axis of (the Class represented by the entry) F3 (= the first Class of column F) can only be such that it bisects the angle between existing mirror planes, otherwise it will either coincide with an already existing mirror plane, or involve an angle of 150 -- implied by taking an angle of 450 -- leading to a forbiddden symmetry.
Addition of a mirror plane parallel to the n-fold axis of F3 and bisecting the angle between existing mirror planes yields F5. See Figure 13.
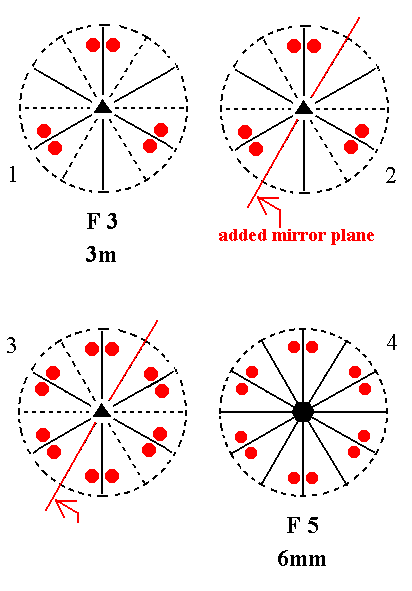
Figure 13. Derivation of F5 from F3.
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 3m represented by the entry F3.
(2). Addition of a mirror plane parallel to the n-fold axis of F3 and bisecting the angle between existing mirror planes.
(3). The added mirror plane generates six more motifs as indicated.
(4). The mirror planes, now present, generate two more vertical mirror planes. The resulting motif pattern demands that the (vertical) n-fold axis, which originally was a 3-fold rotation axis, becomes a 6-fold rotation axis. The symmetry configuration is that of F5.
Addition of a mirror plane parallel to the n-fold axis of F4 is impossible, because it either will coincide with already existing mirror planes, or involve an angle of 1/2(45)0 or smaller, leading to a forbidden symmetry. See Figure 14.
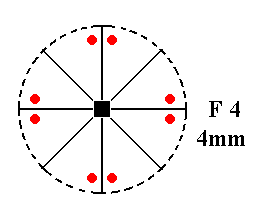
Figure 14. F4---F4.
Addition of a mirror plane parallel to the n-fold axis of F5 is also impossible, because it will either coincide with an existing mirror plane, or involve an angle of 150 or smaller, leading to a forbidden symmetry. See Figure 15.
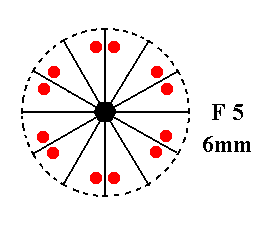
Figure 15. F5---F5.
Summing up : Addition of a mirror plane parallel to the n-fold axis of the Classes of column F generated the following Classes : F5.
Finally we will investigate the addition of a mirror plane parallel to the (vertical) n-fold axis of the Classes of column G.
Addition of a mirror plane parallel to the n-fold axis of G2 (= the first Class of column G) and making angles of 300 and 600 with existing vertical mirror planes, yields G5. See Figure 16.
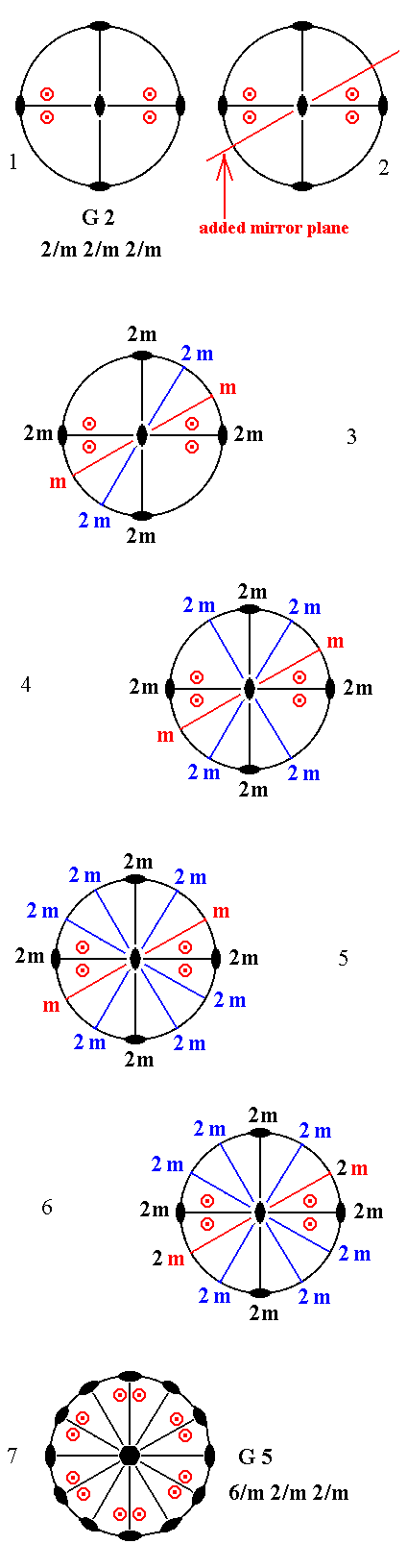 |
Figure 16. G2---G5
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class (2). Addition of a mirror plane parallel to the n-fold axis of G2 and making angles of 300 and 600 with existing mirror planes. (3). The added mirror plane reflects an existing mirror plane (containing a 2-fold rotation axis, and as such indicated by the symbol "2m") lying in the 3 o'clock position, (this reflection) resulting in a 2m at the 1 o'clock position (and, consequently, at the corresponding (opposite) 7 o'clock position).
(4). This generated 2m is itself duplicated by the existing 2m at 12 o'clock, resulting in a 2m at 11 o'clock.
|
Addition of a mirror plane parallel to the n-fold axis of G2 and making angles of 450 with existing vertical mirror planes, yields G4. See Figure 17.
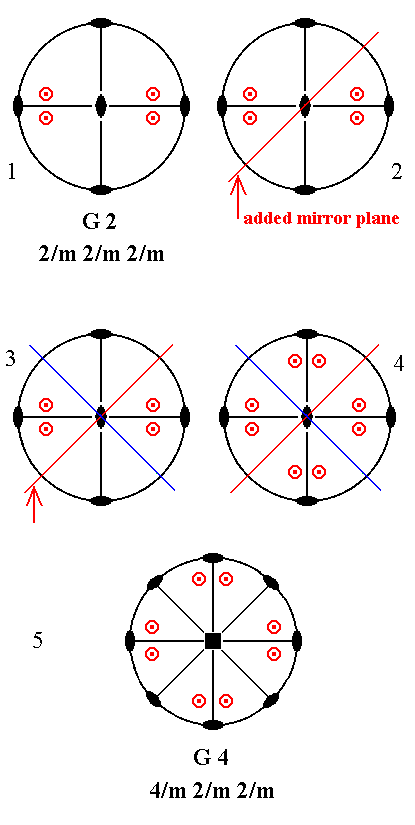 |
Figure 17. G2---G4
(1). Stereogram of the symmetry elements and of the face poles of the most general Form, of the Class 2/m 2/m 2/m represented by the entry G2. |
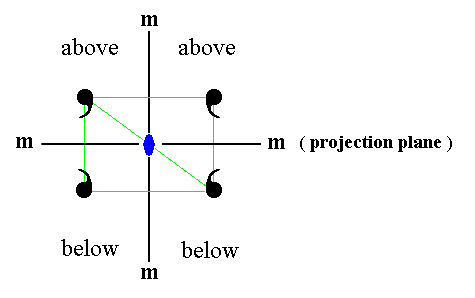 |
Figure 17a. Two mirror planes perpendicular to each other imply a 2-fold rotation axis (small solid blue ellipse) through their line of intersection. |
Addition of a mirror plane parallel to the n-fold axis of G2 and making an angle of 900 with an existing vertical mirror plane does not have any effect because G2 already has vertical mirror planes making an angle of 900 with each other.
Addition of a mirror plane parallel to the n-fold axis of G4 (= the second Class of column G) is not possible because in that case either it coincides with an already existing vertical mirror plane, or forbidden angles become involved.
The same applies to the addition of such a mirror plane to G5.
Summarizing : Addition of a mirror plane parallel to the n-fold axis of the Classes of column G yielded G5 and G4. So nothing new is actually generated.
Now we must add the last symmetry element (from our group of symmetry elements to be added), namely a mirror plane perpendicular to the n-fold axis of the Classes of columns D, E and F (The Classes of column G already have such a mirror plane).
Addition of a mirror plane perpendicular to the (vertical) n-fold axis of the Class represented by the entry D2 (= the first Class of column D) yields G2. See Figure 18.
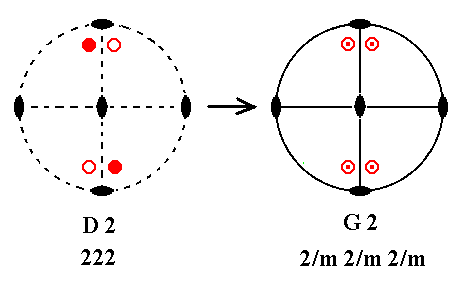
Figure 18. D2---G2.
In Figure 17a we can see that if we have a mirror plane containing a 2-fold axis, then a second mirror plane, perpendicular to the first and also containing that 2-fold axis, is implied. So two new vertical mirror planes are implied, resulting in a symmetry configuration equal to that of G2.
Addition of a mirror plane perpendicular to the n-fold axis of D3 yields E5. See Figure 19.
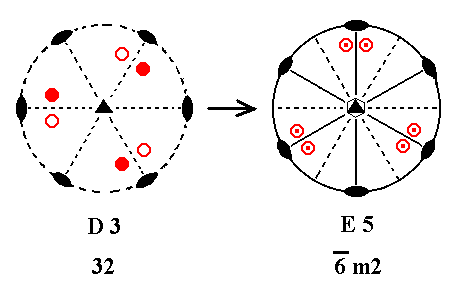
Figure 19. D3---E5.
Like the above case, after adding a horizontal mirror plane, we then have a mirror plane containing horizontal 2-fold axes. Thus these 2-fold axes must be contained in vertical mirror planes. The resulting symmetry configuration is that of E5 ( The stereogram of E5 is (drawn) rotated with respect to that of D3, and its motifs reshuffled, but this is immaterial as far as symmetry is concerned).
Addition of a mirror plane perpendicular to the n-fold axis of D4 yields G4. See Figure 20.
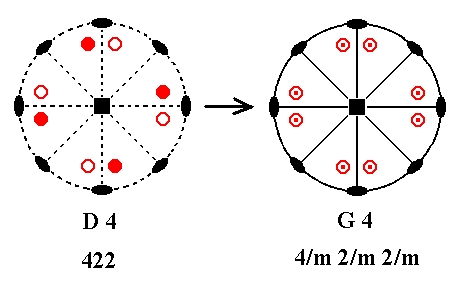
Figure 20. D4---G4.
Also here we get a (horizontal) mirror plane containing horizontal 2-fold axes. These axes will now be contained in vertical mirror planes. The resulting symmetry configuration is that of G4.
Addition of a mirror plane perpendicular to the n-fold axis of D5 yields G5. See Figure 21.
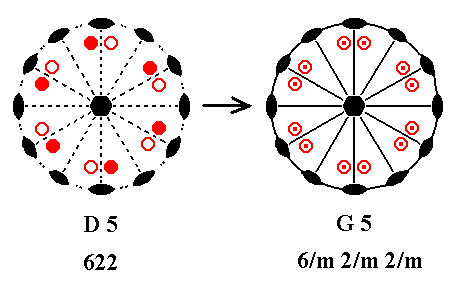
Figure 21. D5---G5.
Also in this case we get a (horizontal) mirror plane containing horizontal 2-fold axes. These axes will now be contained in vertical mirror planes. The resulting symmetry configuration is that of G5.
Summarizing : Addition of a mirror plane perpendicular to the (vertical) n-fold axis of the Classes of column D yielded the following Classes : G2, E5, G4 and G5.
Addition of a mirror plane perpendicular to the n-fold axis of E2 (= the first Class of column E) yields G2. See Figure 22.
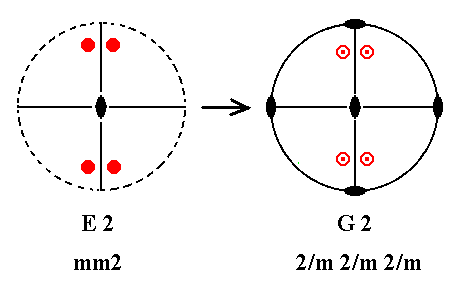
Figure 22. E2---G2.
When we add a horizontal mirror plane we then have the two already existing vertical mirror planes being perpendicular to the added mirror plane. But then 2-fold rotation axes are implied going through the lines of intersection. The resulting symmetry configuration is that of G2.
Addition of a mirror plane perpendicular to the n-fold axis of E3 yields G5. See Figure 23.
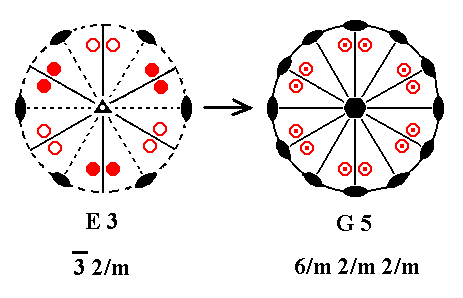
Figure 23. E3---G5.
Addition of a horizontal mirror plane again creates the situation of the already existing vertical mirror planes being perpendicular to the added mirror plane, and thus implying 2-fold axes going through the lines of intersection. Also we now have the originally existing horizonal 2-fold axes lying in a mirror plane (the added horizontal mirror plane), and thus implying vertical mirror planes containing those axes. The resulting symmetry configuration is that of G5.
Addition of a mirror plane perpendicular to the n-fold axis of E4 yields G4. See Figure 24.
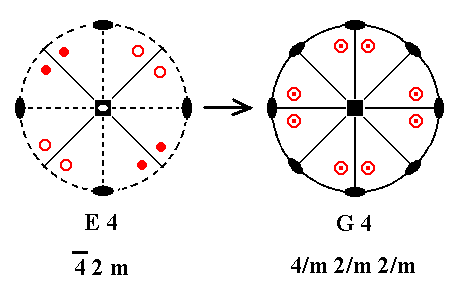
Figure 24. E4---G4.
Addition of a horizontal mirror plane again implies vertical mirror planes and horizontal 2-fold axes as described earlier. The resulting symmetry configuration is that of G4 ( The different position of the motifs as drawn in the stereogram of G4 is immaterial with respect to symmetry because their positions are still general).
Addition of a mirror plane perpendicular to the n-fold axis of E5 yields E5, because it already possesses a horizontal mirror plane. See Figure 25.
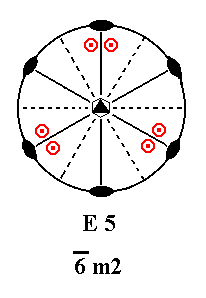
Figure 25. E5---E5.
Summarizing : Addition of a mirror plane perpendicular to the (vertical) n-fold axis of the Classes of column E yielded the folowing Classes : G2, G5, G4 and E5.
Addition of a mirror plane perpendicular to the n-fold axis of F3 (= the first Class of column F) yields E5. See Figure 26.
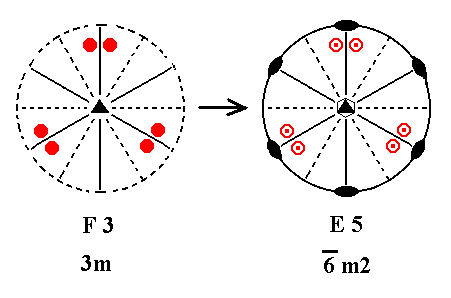
Figure 26. F3---E5.
Addition of a horizontal mirror plane creates the situation of the existing vertical mirror planes being perpendicular to the added mirror plane and thus implying 2-fold axes going through their lines of intersection. The resulting symmetry configuration is that of E5.
Addition of a mirror plane perpendicular to the n-fold axis of F4 yields G4. See Figure 27.
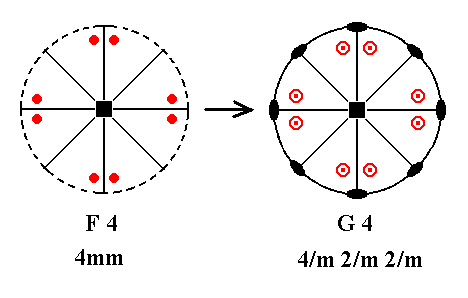
Figure 27. F4---G4.
The added horizontal mirror plane creates the situation of the existing vertical mirror planes being perpendicular to the added mirror plane and thus implying horizontal 2-fold axes going through their lines of intersection. The resulting symmetry configuration is that of G4.
Finally, addition of a mirror plane perpendicular to the n-fold axis of F5 yields G5.
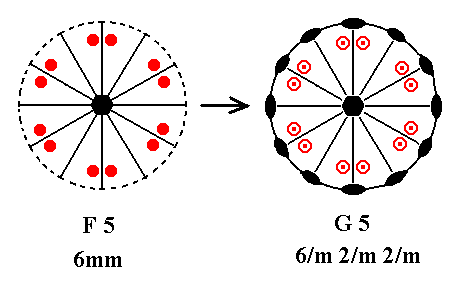
Figure 28. F5---G5.
The added horizontal mirror plane creates the situation of the existing vertical mirror planes being perpendicular to the added mirror plane and thus implying 2-fold axes going through their lines of intersection. The resulting symmetry configuration is that of G5.
Summing up : Addition of a mirror plane perpendicular to the (vertical) n-fold axis of the Classes of column F yielded the following Classes : E5, G4 and G5.
As has been said, the Classes of column G already have a mirror plane perpendicular to the (vertical) n-fold axis, so nothing new will be generated by adding one.
We now have, finally, derived all the 27 Crystal Classes of our table (given in Part One), and have shown that these are the only Classes having at most one more-than-2-fold axis.
It remains to derive all the Crystal Classes having more than one more-than-2-fold rotation axis (They are the Classes of the Isometric Crystal System).
To continue, click HERE for Part Five.
****************