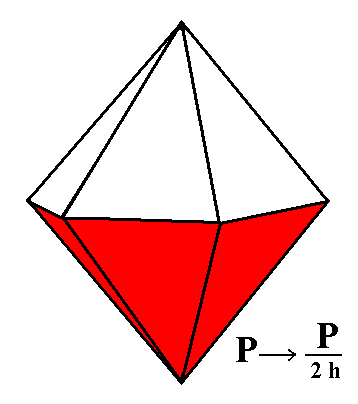
Protopyramid (= hexagonal type I bipyramid)
Deuteropyramid (= hexagonal type II bipyramid)
Dihexagonal Bipyramid
Protoprism (= hexagonal type I prism)
Deuteroprism (= hexagonal type II prism)
Dihexagonal Prism
Basic Pinacoid
When we suppress the horizontal mirror plane of the hexagonal protopyramid we obtain two independent halves of it. Of course they can combine with each other again but also in this case the horizontal mirror plane is still absent and the main axis is still polar. See Figure 1, 2 and 3.
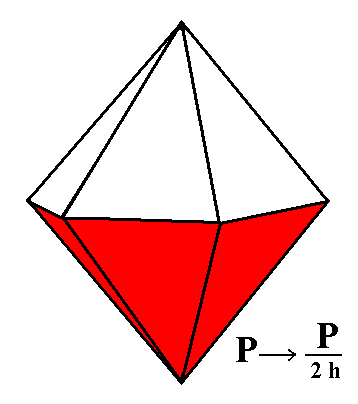 |
Figure 1. Red faces are suppressed, white faces are allowed to extend, or, white faces are suppressed, red faces are allowed to extend (in virtue of the suppression of the horizontal mirror plane). This yields two independent monopyramids. |
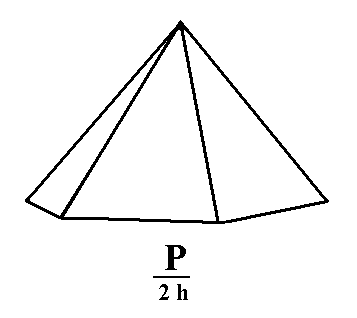 |
Figure 2. Hexagonal Type I Monopyramid (hemimorphic pyramid) generated from the white faces of the pyramid of Figure 1. |
The straight lines bordering the basis of this monopyramid (Figure 2 and 3) do not indicate the presence of a basis of this pyramid in the sense of a face (the seventh face of the pyramid). The pyramid lacks such a face, it is an open Form. So we should in fact indicate the pyramid as having no boundaries at its lower end (because it doesn't have such an end). Often one indicates this by drawing these lines irregularly, as if the pyramid was broken off at its lower end. We here however stick to drawing them as straight lines for reasons of clarity.
Only by means of a combination with another Form, the Pedion (see below), could the pyramid be closed at its bottom by one flat face.
The "h" in the expression "2h" of the Naumann symbol for this Form indicates that the applied hemihedric is a hemimorphy.
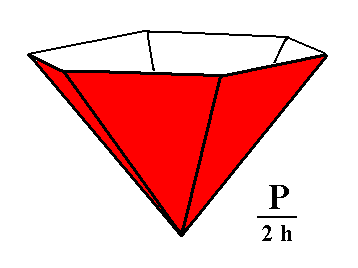 |
Figure 3. Hexagonal Type I Monopyramid (hemimorphic pyramid) generated from the red faces of the pyramid of Figure 1. |
From the holohedric deuteropyramid two independent type II hexagonal monopyramids can be derived by applying hemimorphy (= suppression of the horizontal mirror plane). They are open Forms. See Figure 3a.
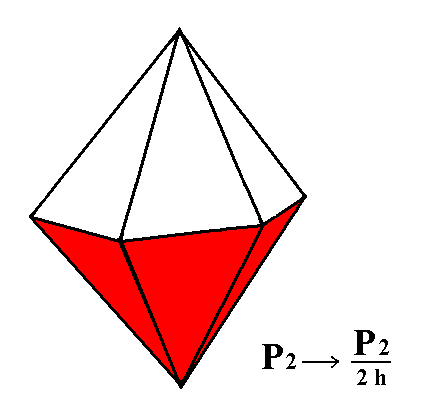 |
Figure 3a. By suppressing either the red faces or the white faces (as a result of suppression of the horizontal mirror plane) of the holohedric Deuteropyramid, a Type II Hexagonal Monopyramid can be generated. See Figures 3b and 3c. |
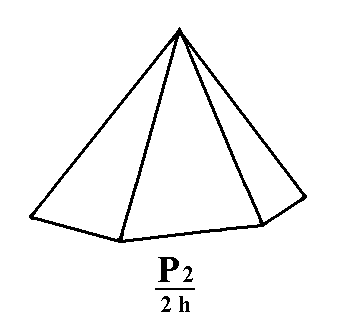 |
Figure 3b. A Type II Hexagonal Monopyramid is generated from the white faces of the holohedric Deuteropyramid of Figure 3a. |
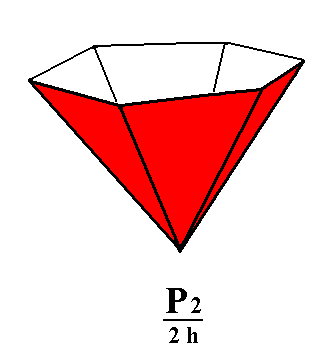 |
Figure 3c. A Type II Hexagonal Monopyramid is generated from the red faces of the holohedric Deuteropyramid of Figure 3a. |
From the dihexagonal bipyramid we can derive a dihexagonal monopyramid (by applying hemimorphy), yet another Form of this Crystal Class.
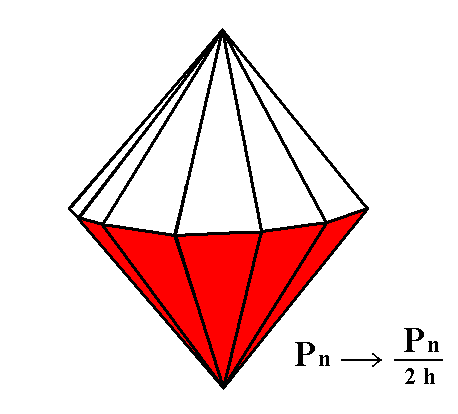 |
Figure 4. The red faces of the Dihexagonal Bipyramid are suppressed by hemimorphy while the white faces are allowed to extend themselves, or vice versa. Two dihexagonal monopyramids are generated in this way. |
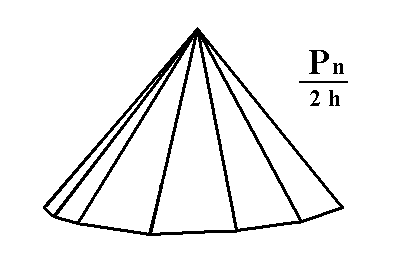 |
Figure 5. Dihexagonal Monopyramid, derived from the white faces of the Dihexagonal Bipyramid of Figure 4. Any horizontal section of it is a dihexagon. The higher up the section is taken the smaller the resulting dihexagon. |
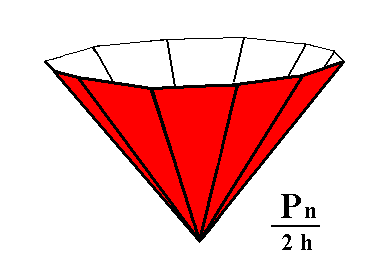 |
Figure 6. Dihexagonal Monopyramid, derived from the red faces of the Dihexagonal Bipyramid of Figure 4. Any horizontal section of it is a dihexagon. The lower down the section is taken the smaller the resulting dihexagon. |
From the protoprism we can derive (by applying hemimorphy) the type I hexagonal prism. This hemimorphic prism has the same shape as the holohedric protoprism, but possesses nonetheless a lower symmetry than the latter. It lacks a horizontal mirror plane which becomes evident in certain physical properties.
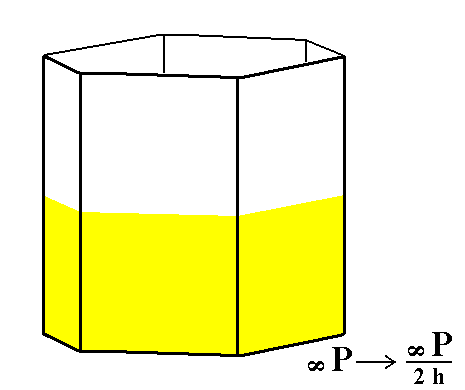 |
Figure 7. The hemimorphic Type I Hexagonal Prism can be derived from the holohedric Hexagonal Protoprism. Because the suppressed mirror plane is perpendicular to the faces no loss of faces will result. |
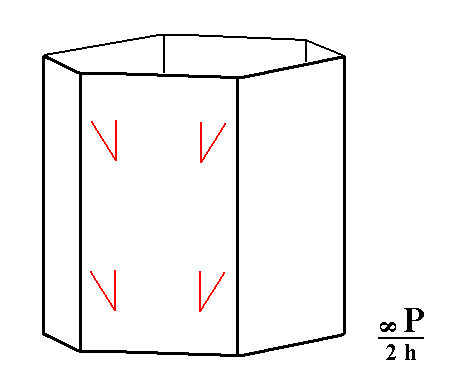 |
Figure 8. The hemimorphic Type I Hexagonal Prism. The marks indicate the absence of the horizontal mirror plane. |
When hemimorphy is applied to the holohedric hexagonal deuteroprism we get a hemimorphic Type II hexagonal prism. Because the suppressed mirror plane is perpendicular to the faces no loss of faces will be effected. See Figures 9 and 10.
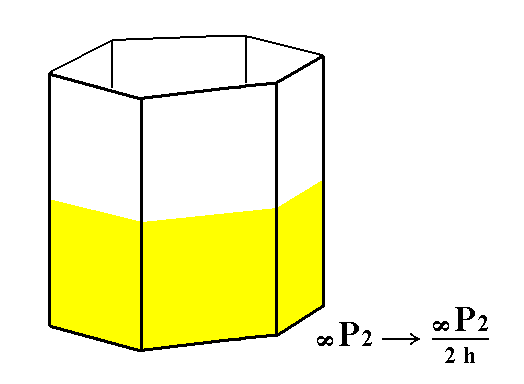
Figure 9. From the holohedric Deuteroprism the hemimorphic Type II Hexagonal Prism can be derived.
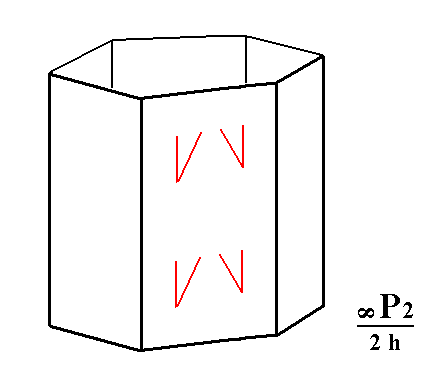
Figure 10. The hemimorphic Type II Hexagonal Prism. It has the same shape as the holohedric Deuteroprism. The marks indicate the absence of the horizontal mirror plane.
The next Form to be derived is the hemimorphic dihexagonal prism. It is derived from the holohedric dihexagonal prism. Seem Figures 11 and 12.
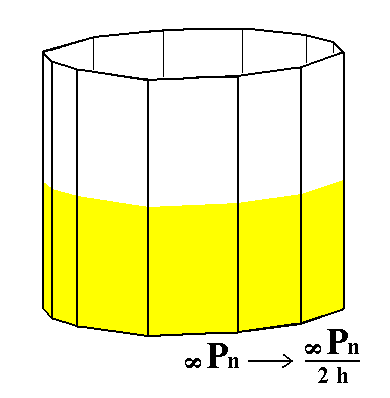 |
Figure 11. The hemimorphic Dihexagonal Prism can be derived from the holohedric Dihexagonal Prism by suppressing the horizontal mirror plane of the latter. Because this plane is perpendicular to the faces no loss of faces is effected, but the resulting prism has lower symmetry (See Figure 12.). |
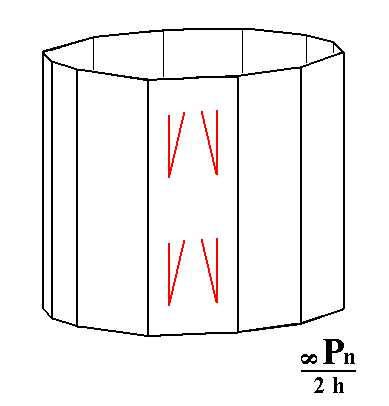 |
Figure 12. The hemimorphic Dihexagonal Prism. The absence of a horizontal mirror plane is indicated by marks. |
The final Form of this Crystal Class is the pedion. It is derived from the holohedric basic pinacoid, by suppressing the horizontal mirror plane of this Form. Two pedions are in fact derived this way, an upper one and a lower one, which are independent of each other. They (i.e. two pedions) can close a hemimorphic prism at its top and at its bottom, or one of them can close a prism at, say, its top, while that prism is closed at its bottom by another Form of this Class, for instance a monopyramid with its top down (like in Figure 6, 3c, or 3).
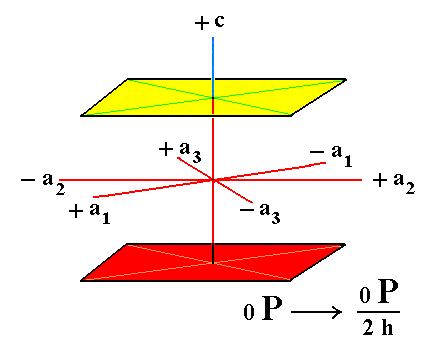
Figure 13. The hemimorphic Pedion can be derived from the holohedric Basic Pinacoid by suppressing the horizontal mirror plane (i.e. the equatorial mirror plane, lying between its faces), resulting in suppression of either the yellow face or the red face. In this way two independent Pedions, an upper one and a lower one can be generated. See Figures 14 and 15.
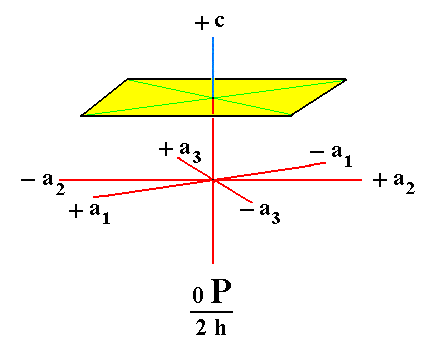
Figure 14. A hemimorphic Pedion (Monohedron), generated from the yellow face of the holohedric Basic Pinacoid of Figure 13.
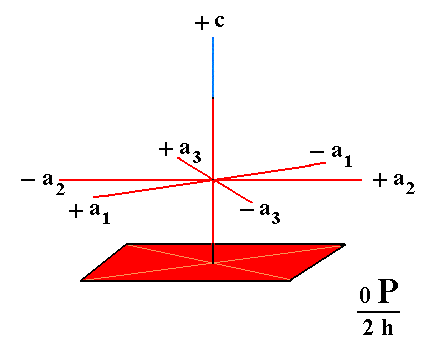
Figure 15. A hemimorphic Pedion (Monohedron), generated from the red face of the holohedric Basic Pinacoid of Figure 13.
This concludes the derivation of all the Forms of the Dihexagonal-pyramidal Crystal Class (= hemimorphy of holohedric) by means of the Merohedric Approach.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Dihexagonal-pyramidal Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :
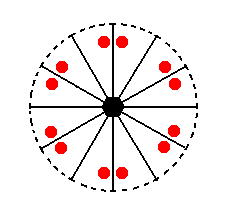 |
Figure 16. Stereogram of the symmetry elements of the Dihexagonal-pyramidal Crystal Class, and of all the faces of the most general Form. |
The face a : ~a : -a : c is parallel to the a2 axis. Its position in the stereographic projection is given in (1) of Figure 17, and the generation of the Form -- the type I hexagonal monopyramid -- is given in (2) of Figure 17.
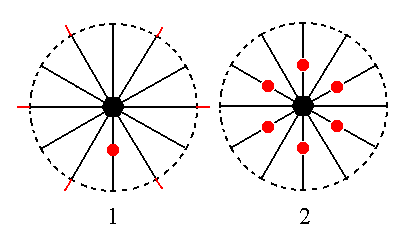
Figure 17. (1). Position of the face a : ~a : -a : c in the stereographic projection of the symmetry elements of the Dihexagonal-pyramidal Crystal Class. The three horizontal crystallographic axes are indicated. (2). Generation of a configuration of faces that as a whole complies with the symmetries of the Class. Generated is a Type I Hexagonal monopyramid.
The face 2a : 2a : -a : c cuts off twice the unit length of two horizontal crystallographic axes, while from the third horizontal axis and from the vertical axis it cuts off a piece of unit length (i.e. the a3 intercept and the c intercept both are equal to the corresponding intercepts in the protopyramid which are set equal to 1).
The position of the face and the generation of the Type II hexagonal monopyramid in stereographic projection is depicted in Figure 18. The face is multiplied six times in virtue of the 6-fold rotation axis. The remaining symmetry elements have no further effect anymore.
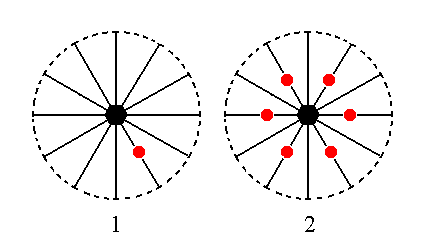
Figure 18. (1). Position of the face 2a : 2a : -a : c in the stereogaphic projection of the symmetry elements of the Dihexagonal-pyramidal Crystal Class. (2). Generation of the Type II Hexagonal Monopyramid.
The face [3/2]a : 3a : -a : c is a definite face and can be indicated precisely in the stereographic projection of the symmetry elements of the present Crystal Class. It is however just as instructive to take the general form of this face, namely [s/(s-1)]a : sa : -a : c, and depict the position of this general face in the stereographic projection. Its location should be somewhere between the locations of the two faces discussed above.
Figure 19 shows this location and the generation of the corresponding Form, namely the dihexagonal monopyramid. This generation goes as follows : Because the face does not lie perpendicular to one of the (vertical) mirror planes (contrary to the case of each of the above discussed faces), the face is duplicated by that mirror plane, resulting in two faces making an angle (smaller than 1800) with each other. Next this pair will be multiplied six times in virtue of the 6-fold rotation axis, resulting in a dihexagonal monopyramid. The remaining symmetry elements do not add anything further.
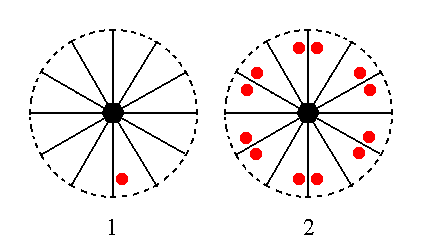
Figure 19. (1). Position of the face [s/(s-1)]a : sa : -a : c in the stereographic projection of the symmetry elements of the Dihexagonal-pyramidal Crystal Class. (2). Generation of the Dihexagonal Monopyramid.
The face [3/2]a : 3a : -a : ~c is vertical. Horizontally it has the same orientation as the face just discussed above. For the stereographic picture we will take the generalized face, namely [s/(s-1)]a : sa : -a : ~c. The position of this face, as well as the Form -- the dihexagonal prism generated from it is shown in stereographic projection in Figure 20.
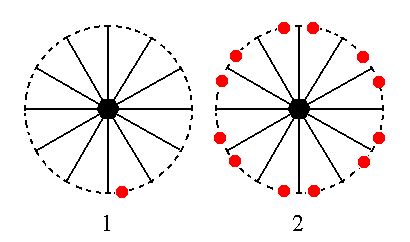
Figure 20. (1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereographic projection of the symmetry elements of the Dihexagonal-pyramidal Crystal Class. (2). Stereogram of the generated Form, the hemimorphic Dihexagonal Prism.
Like the case of the dihexagonal pyramid, the face is duplicated by a mirror plane, resulting in a face pair consisting of two non-parallel faces. Next this pair is multiplied six times in virtue of the 6-fold rotation axis.
The face a : ~a : -a : ~c is also vertical. Its horizontal orientation is the same as that of the first discussed face. Its position and the Form generated from it is stereographically depicted in Figure 21.
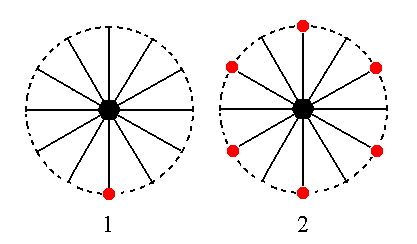
Figure 21. (1). Position of the face a : ~a : -a : ~c in the stereographic projection of the symmetry elements of the Dihexagonal-pyramidal Crystal Class. (2). Generation of a hemimorphic Type I Hexagonal Prism.
Because this face is perpendicular to the mirror plane on the stereographic trace of which its face pole lies (i.e. the mirror plane lying between the a1 axis and the a3 axis), it is not duplicated (by that mirror plane). But it is multiplied six times in virtue of the 6-fold rotation axis. The resulting configuration of faces (a Form) is a hemimorphic Type I hexagonal prism.
The face 2a : 2a : -a : ~c is also vertical. Its horizontal orientation is the same as the second face from the above list of basic faces. Its position in the stereographic projection as well as that of the faces generated from it -- together constituting the hemimorphic Type II Hexagonal Prism -- is given in Figure 22.
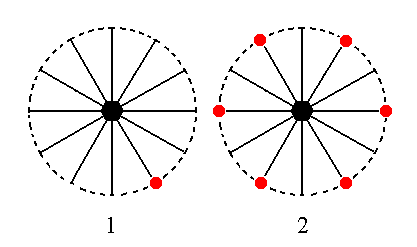
Figure 22. (1). Position of the face 2a : 2a : -a : ~c in the stereographic projection of the symmetry elements of the Dihexagonal-pyramidal Crystal Class. (2). Stereogram of the hemimorphic Type II Hexagonal Prism.
The last face -- ~a : ~a : ~a : c -- is horizontal. The vertical mirror planes do not multiply this face, and also the 6-fold rotation axis does not generate more faces. So the resulting Form is this same face, a pedion (monohedron). Its position in the stereographic projection is shown in Figure 23.
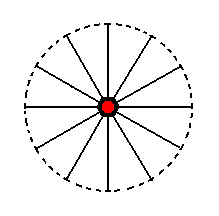 |
Figure 23. Stereogram of the Pedion, generated from the face ~a : ~a : ~a : c . |
This concludes our exposition of the Dihexagonal-pyramidal Crystal Class.
To continue, klick HERE for Part Three (Class 6/m).