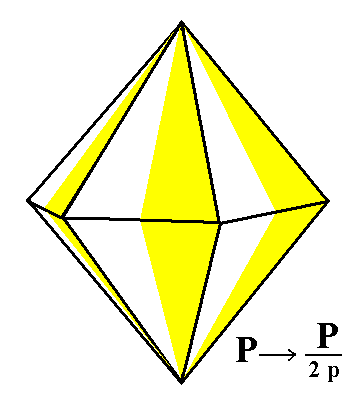
The "p" in the expression "2p" of the Naumann symbol expresses the fact that we here have to do with the pyramidal hemihedric (of the Hexagonal Crystal System).
Protopyramid (= hexagonal type I bipyramid)
Deuteropyramid (= hexagonal type II bipyramid)
Dihexagonal Bipyramid
Protoprism (= hexagonal type I prism)
Deuteroprism (= hexagonal type II prism)
Dihexagonal Prism
Basic Pinacoid
From the holohedric protopyramid we can derive the pyramidal hemihedric Type I hexagonal bipyramid by suppression of all the vertical mirror planes.
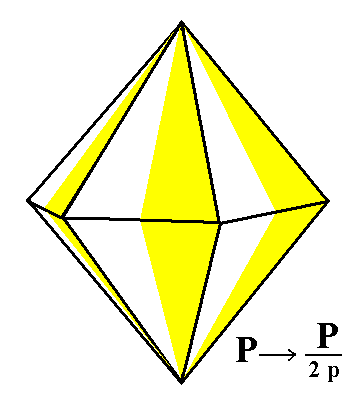 |
Figure 1. Suppression of the vertical mirror planes of the holohedric Protopyramid does not result in a reduction of faces, because each face is perpendicular to one or another suppressed mirror plane. If we let dissappear the colored halves of the faces (expressing the suppression of the mirror planes), the subsequent extension of the surviving halves will recover the original pyramid, but now having a lower symmetry. The "p" in the expression "2p" of the Naumann symbol expresses the fact that we here have to do with the pyramidal hemihedric (of the Hexagonal Crystal System). |
Also the holohedric deuteropyramid will not change its external shape when subjected to the pyramidal hemihedric. The result is a pyramidal hemihedric Type II hexagonal bipyramid. See Figure 2.
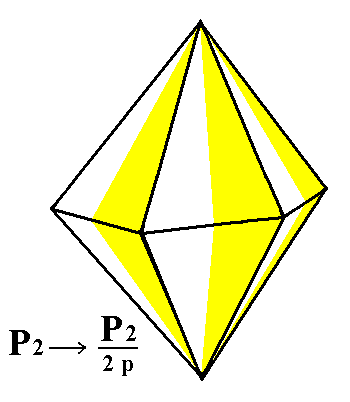 |
Figure 2. Suppression of the vertical mirror planes of the holohedric Deuteropyramid does not result in a reduction of faces, because each face is perpendicular to one or another suppressed mirror plane. If we let dissappear the colored halves of the faces (expressing the suppression of the mirror planes), the subsequent extension of the surviving halves will recover the original pyramid, but now having a lower symmetry. Again the "p" in the expression "2p" of the Naumann symbol expresses the fact that we here have to do with the pyramidal hemihedric (of the Hexagonal Crystal System). |
From the dihexagonal bipyramid we can derive a pyramidal hemihedric Type III hexagonal bipyramid (= pyramidal hemihedric tritopyramid). So here the application of the pyramidal hemihedric effects a change in shape : from a dihexagonal bipyramid we get a hexagonal bipyramid, like the hexagonal type I and type II bipyramids, but with a different orientation with respect to the crystallographic axes. The best way to show what happens to the faces of the dihexagonal bipyramid is to consider its equatorial plane. We can then clearly see the orientations and the number of faces of the several bipyramids.
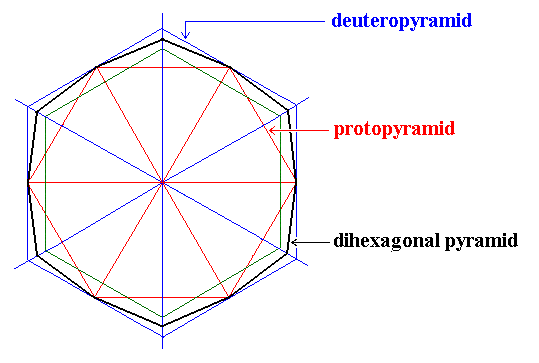
Figure 3. Equatorial planes of the Hexagonal Protopyramid, the Hexagonal Deuteropyramid and the Dihexagonal pyramid. The three horizontal (equatorial) crystallographic axes are indicated (red), and also their bisectors (blue).
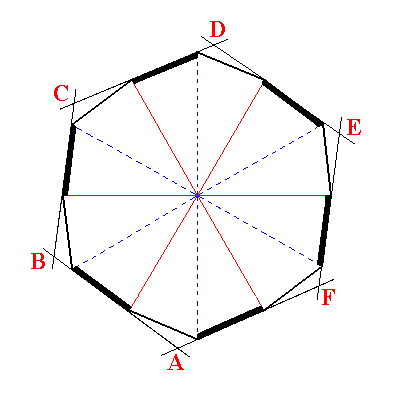
Figure 4. Generation of the equatorial plane of the Hexagonal Tritopyramid (= Type III hexagonal bipyramid) from the equatorial plane of the Dihexagonal Bipyramid by alternately suppressing half of the sides (in virtue of the suppression of all the vertical mirror planes) and extending the survived sides till they meet. The equatorial plane of the generated Tritopyramid is indicated by A B C D E F.
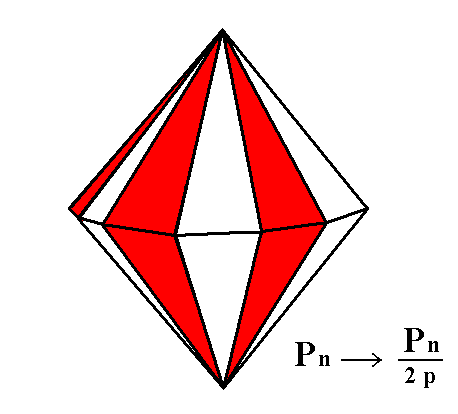
Figure 5. Generation of the Hexagonal Tritopyramid from the Dihexagonal Bipyramid, by applying pyramidal hemihedric to the latter. Two Tritopyramids can be derived, depending on which set of faces (the red ones or the white ones) is suppressed.
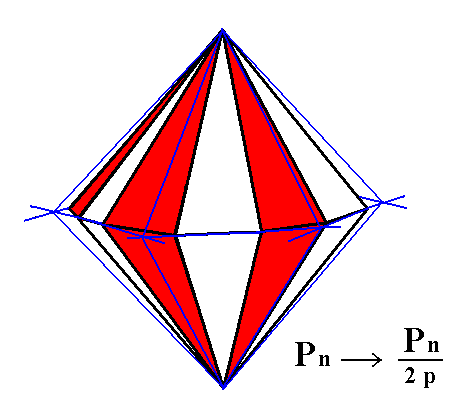
Figure 6. Construction of a Hexagonal Tritopyramid from the white faces of the Dihexagonal Bipyramid. A similar pyramid (but with a slightly different orientation) can be constructed from the red faces.
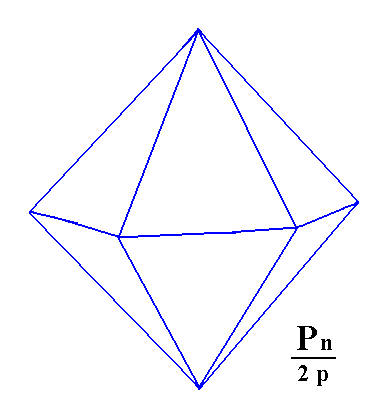
Figure 7. Result of the construction of a Hexagonal Tritopyramid (= Type III Hexagonal Bipyramid) from the white faces of a Dihexagonal Bipyramid.
By applying pyramidal hemihedric to the holohedric hexagonal protoprism we get a pyramidal hemihedric type I hexagonal prism, having the same shape as the holohedric one, but possessing less symmetry (that can, like all cases of geometrically (morphologically) unchanged Forms, be detected physically). See Figure 8.
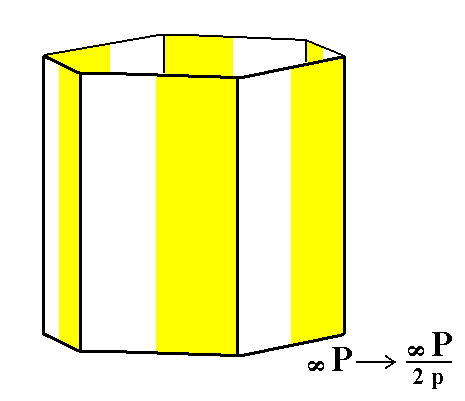
Figure 8. Generation (derivation) of the pyramidal hemihedric Type I Hexagonal Prism from the holohedric Protoprism. Because the suppression of either the colored or the white regions, followed by extension of the surviving regions, does not result in a loss of faces the hemihedric prism has the same external shape as the holohedric prism.
By applying pyramidal hemihedric to the holohedric deuteroprism we get a pyramidal hemihedric type II hexagonal prism having the same shape as the holohedric one.
See Figure 9.
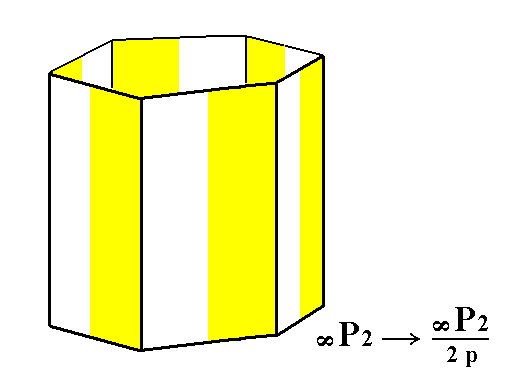
Figure 9. Generation of the pyramidal hemihedric Type II Hexagonal Prism from the holohedric hexagonal Deuteroprism.
By applying pyramidal hemihedric to the holohedric dihexagonal prism we get a hexagonal tritoprism (= type III hexagonal prism), in the same way as in the case of the derivation of the pyramidal hemihedric tritopyramid from the holohedric dihexagonal pyramid.
See Figure 10, 11 and 12.
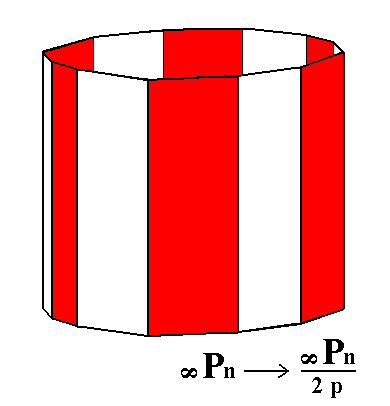
Figure 10. Derivation of the pyramidal hemihedric Type III Hexagonal Prism (= pyramidal hemihedric Hexagonal Tritoprism) from the holohedric Dihexagonal Prism.
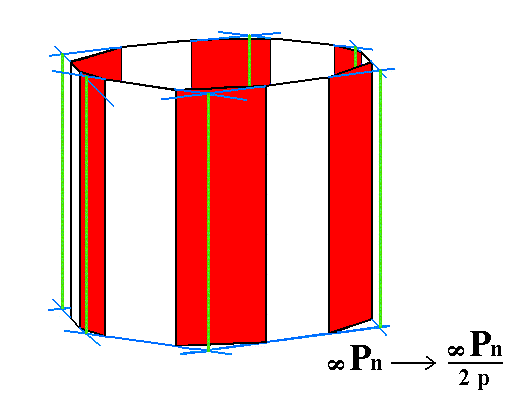
Figure 11. Actual construction of a pyramidal hemihedric Tritoprism, by means of suppression of the red faces and extension of the white faces till they meet. A similar hexagonal prism can be constructed by suppression of the white faces and extension of the red ones.
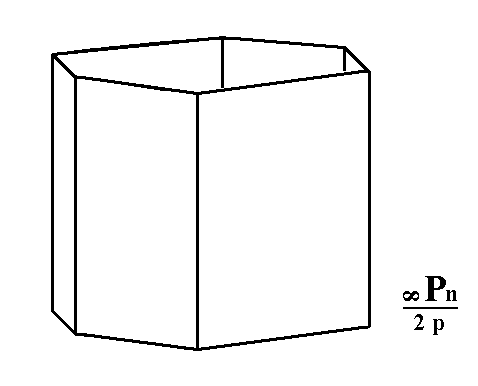
Figure 12. A pyramidal hemihedric Tritoprism, generated from the white faces of the Dihexagonal Prism of the Figures 10 and 11.
If, finally, we apply the pyramidal hemihedric to the holohedric basic pinacoid, the result -- the pyramidal hemihedric basic pinacoid -- will have the same shape, but its symmetry is lowered accordingly. See Figure 13.
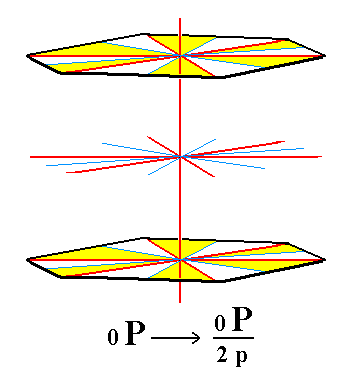
Figure 13. Suppression of the vertical mirror planes of the holohedric Basic Pinacoid does not result in a reduction of faces, because both faces are perpendicular to those suppressed mirror planes. If we let dissappear the colored regions of the faces (expressing the suppression of the mirror planes), the subsequent extension of the surviving (white) regions will recover the original faces, and thus the Basic Pinacoid, but the latter now having a lower symmetry.
Indicated are the four crystallographic axes (red) and the bisectors of the equatorial crystallographic axes.
Again the "p" in the expression "2p" of the Naumann symbol expresses the fact that we here have to do with the pyramidal hemihedric (of the Hexagonal Crystal System).
This concludes our derivation of all the Forms of the Hexagonal-Bipyramidal Crystal Class by means of the Merohedric Approach.
All these Forms can engage in combinations in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Hexagonal-bipyramidal Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :
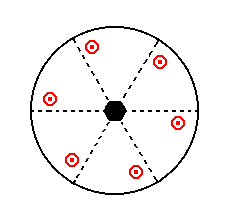 |
Figure 14. Stereogram of the symmetry elements of the Hexagonal-bipyramidal Crystal Class, and of all the faces of the most general Form. |
The face a : ~a : -a : c cuts off a piece of unit length from the a1 axis, it is parallel to the a2 axis, and cuts off a piece of unit length from the (negative end of the) a3 axis and from the c axis as well. Its position in the stereographic projection of the symmetry elements of the present Class, and the generation of the Form by subjecting this face to the symmetry elements of the Class, is shown in Figure 15. In generating the Form this face is multiplied six times in virtue of the 6-fold rotation axis, resulting in a hexagonal monopyramid. Next this monopyramid will be duplicated because of the equatorial mirror plane. The result is a pyramidal hemihedric type I hexagonal bipyramid.
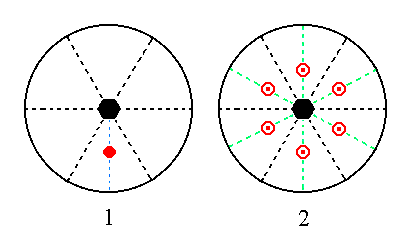
Figure 15. (1). The position of the face a : ~a : -a : c and (2) the generation of the pyramidal hemihedric Type I Hexagonal Bipyramid in the stereographic projection of the symmetry elements of the Hexagonal-bipyramidal Crystal Class.
The face 2a : 2a : -a : c cuts off a piece of unit length from the (negative end of the) a3 axis, and from the c axis, and cuts off twice a unit length from the a1 axis and also from the a2 axis. Its position in the stereographic projection, and the positions of the faces of the generated Form in that stereographic projection are shown in Figure 16. The face will be multiplied six times in virtue of the 6-fold rotation axis, resulting in a hexagonal monopyramid. Next this monopyramid is duplicated in virtue of the equatorial mirror plane. The result is a pyramidal hemihedric Type II hexagonal bipyramid.
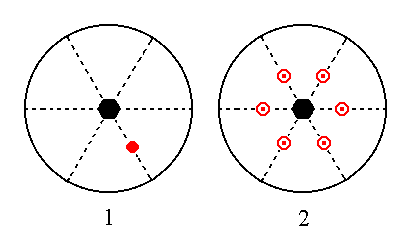
Figure 16. (1). Position of the face 2a : 2a : -a : c in the stereographic projection of the symmetry elements of the Hexagonal-bipyramidal Crystal Class. (2)The positions of the faces of the generated Form.
The face [3/2]a : 3a : -a : c is a definite face. Here we will consider the generalized version of it, namely the face [s/(s-1)]a : sa : -a : c. Its position in the stereographic projection, and the generation of the Form is depicted in Figure 17. The face will be multiplied six times in virtue of the 6-fold rotation axis, resulting in a hexagonal monopyramid. Then this monopyramid will be duplicated by the equatorial mirror plane, resulting in a pyramidal hemihedric type III hexagonal bipyramid (= pyramidal hemihedric hexagonal tritopyramid) .
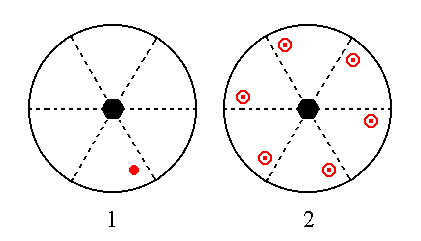
Figure 17. (1). Position of the face [s/(s-1)]a : sa : -a : c in the stereographic projection of the symmetry elements of the Hexagonal-bipyramidal Crystal Class. (2). Generation of the faces of the general Form in stereographic projection.
The face [3/2]a : 3a : -a : ~c is like the previous one but now vertically oriented. Its generalized version is [s/(s-1)]a : sa : -a : ~c. Its position, and the generation of all the faces of the Form is depicted in stereographic projection in Figure 18. The face is multiplied six times in virtue of the 6-fold rotation axis, resulting in a hexagonal prism. The equatorial mirror plane does not have any further effect in the sense of generating still more faces. So the result is a pyramidal hemihedric type III hexagonal prism (= pyramidal hemihedric hexagonal tritoprism).
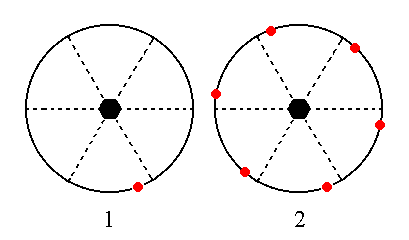
Figure 18. (1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-bipyramidal Crystal Class. (2). Stereogram of the pyramidal hemihedric Tritoprism.
The face a : ~a : -a : ~c is also vertical. Its position in the stereographic projection and the generation of all the faces of the Form is depicted in Figure 19. The face is multiplied six times in virtue of the 6-fold rotation axis, resulting in a hexagonal prism. The equatorial mirror plane does not have any further effect, so the resulting Form is a pyramidal hemihedric type I hexagonal prism.
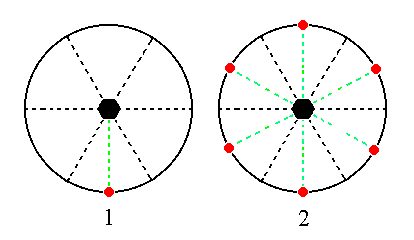
Figure 19. (1). Position of the face a : ~a : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-bipyramidal Crystal Class. (2). Stereogram of the generated pyramidal hemihedric Type I Hexagonal Prism.
The face 2a : 2a : -a : ~c is also vertical. Its position in the stereographic projection and the generation of all the faces of the Form is shown in Figure 20. The face will be multiplied six times in virtue of the 6-fold rotation axis, resulting in a hexagonal prism. The equatorial mirror plane does not have any further effect, so the resulting Form is a pyramidal hemihedric type II hexagonal prism.
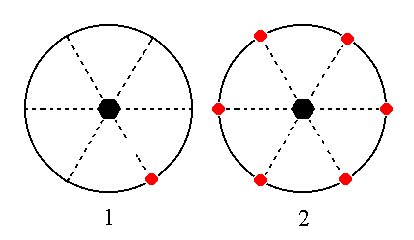
Figure 20. (1). Position of the face 2a : 2a : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-bipyramidal Crystal Class. (2). Generation of all the faces of the pyramidal hemihedric Type II Hexagonal Prism.
The face ~a : ~a : ~a : c is horizontal. Its position and the generation of the Form is depicted stereographically in Figure 21. If we subject this face to the 6-fold rotation axis no new faces are generated, but the equatorial mirror plane duplicates it, resulting in a Form consisting of two parallel horizontal faces, the pyramidal hemihedric basic pinacoid.
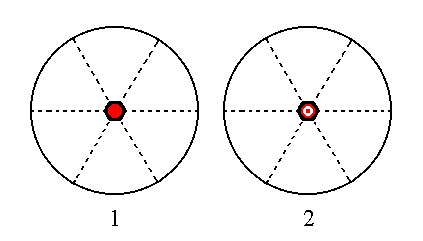
Figure 21. (1). Position of the face ~a : ~a : ~a : c in the stereographic projection of the symmetry elements of the Hexagonal-bipyramidal Crystal Class. (2). Generation of the pyramidal hemihedric Basic Pinacoid.
This concludes our exposition of the Hexagonal-bipyramidal Crystal Class.
To continue, klick HERE for Part Four (Class 6).