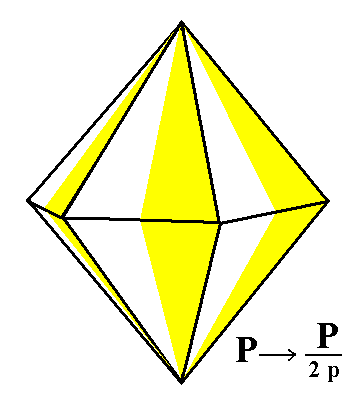
The holohedric Protopyramid (= hexagonal type I bipyramid) gave rise to the pyramidal hemihedric Type I hexagonal bipyramid.
The holohedric Deuteropyramid (= hexagonal type II bipyramid) gave rise to the pyramidal hemihedric Type II hexagonal bipyramid.
The holohedric Dihexagonal Bipyramid gave rise to the pyramidal hemihedric Type III hexagonal bipyramid (= pyramidal hemihedric tritopyramid).
The holohedric Protoprism (= hexagonal type I prism) gave rise to the pyramidal hemihedric type I hexagonal prism.
The holohedric Deuteroprism (= hexagonal type II prism) gave rise to the pyramidal hemihedric type II hexagonal prism.
The holohedric Dihexagonal Prism gave rise to the pyramidal hemihedric hexagonal tritoprism (= type III hexagonal prism).
The holohedric Basic Pinacoid gave rise to the pyramidal hemihedric basic pinacoid.
From these pyramidal hemihedric Forms we will now derive the Forms of the present Class (the Hexagonal-pyramidal Class), by suppressing their equatorial mirror plane.
We begin with the pyramidal hemihedric type I hexagonal bipyramid, shown in Figure 1.
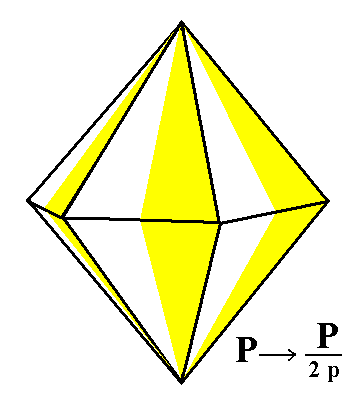 |
Figure 1. The pyramidal hemihedric Type I Hexagonal Bipyramid. |
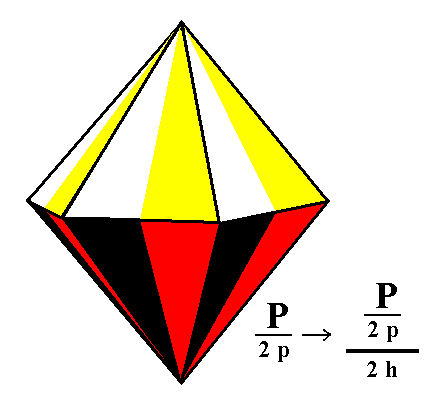 |
Figure 2. The pyramidal hemihedric Type I Hexagonal Bipyramid is deprived of its equatorial mirror plane. Two independent monopyramids are the result, when either the faces of the top halve are suppressed (in virtue of the suppression of the equatorial mirror plane) or the faces of the bottom halve . |
In Figure 2 we show the removal of the equatorial mirror plane. The Naumann symbol of the generated Form expresses the fact that a pyramidal hemihedric Form has been subjected to hemimorphy, (this hemimorphy) symbolized by "/ 2h".
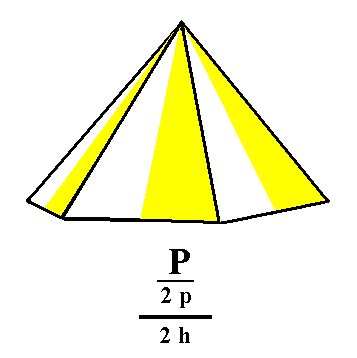 |
Figure 3. The hemimorphic pyramidal hemihedric Type I Hexagonal Monopyramid, derived from the top faces of the pyramidal hemihedric Type I Hexagonal Bipyramid. |
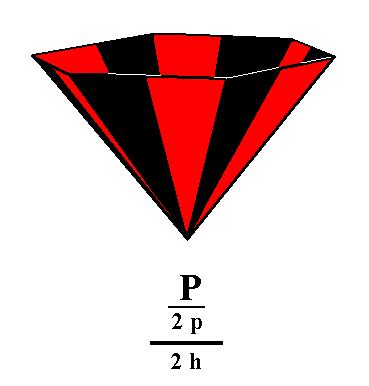 |
Figure 4. The hemimorphic pyramidal hemihedric Type I Hexagonal Monopyramid, derived from the lower faces of the pyramidal hemihedric Type I Hexagonal Bipyramid. |
The straight lines bordering the lower part of the pyramid of Figure 3, and the upper part of the pyramid of Figure 4, should not suggest that each of these pyramids is closed by a horizontal face. Both pyramids are open Forms and cannot exist just like that, but only in one or another combination, either with each other or, with another Form of this Class, for instance a pedion. In the latter case such a pyramid is closed by a horizontal face.
Here (i.e. in Figure 3 and 4) we depict the monopyramid with the straight lines mentioned for reasons of clarity (i.e. to let clearly come out the pyramidal shape of these Forms).
The next Form is derived from the pyramidal hemihedric Type II hexagonal bipyramid. Again we will obtain two independent halves of this pyramid, i.e. two hemimorphous pyramidal hemihedric type II hexagonal monopyramids. See Figure 5, 6, 7 and 8.
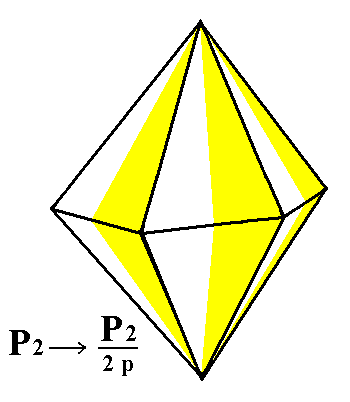 |
Figure 5. The pyramidal hemihedric Type II Hexagonal Bipyramid. |
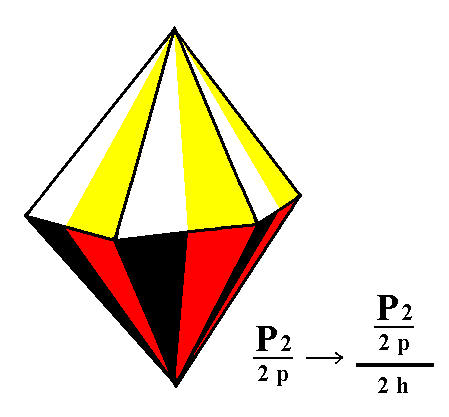
Figure 6. The Hexagonal Type II Bipyramid looses its equatorial mirror plane, yielding two independent halves.
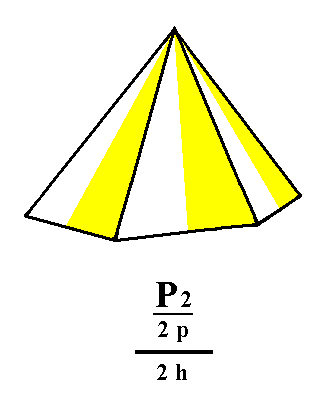 |
Figure 7. The hemimorphous pyramidal hemihedric Type II Hexagonal Monopyramid, derived from the upper faces of the bipyramid of Figure 6. |
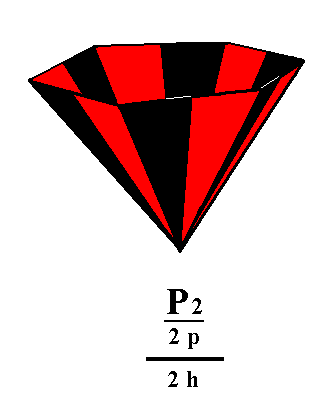 |
Figure 8. The hemimorphous pyramidal hemihedric Type II Hexagonal Monopyramid, derived from the lower faces of the bipyramid of Figure 6. |
From the pyramidal hemihedric Type III hexagonal bipyramid also two independent halves are generated by applying hemimorphy, namely two hemimorphous pyramidal hemihedric type III hexagonal monopyramids. See Figures 9, and 10.
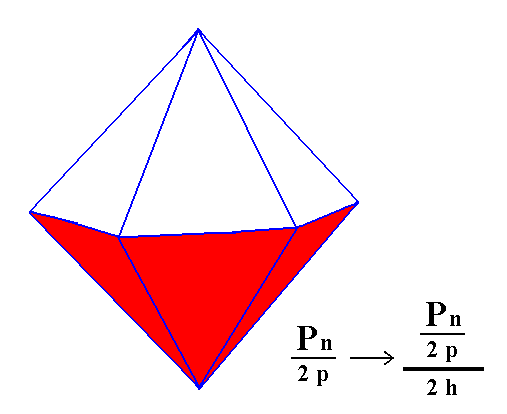
Figure 9. The pyramidal hemihedric Type III Hexagonal Bipyramid looses its equatorial mirror plane, resulting in two independent halves.
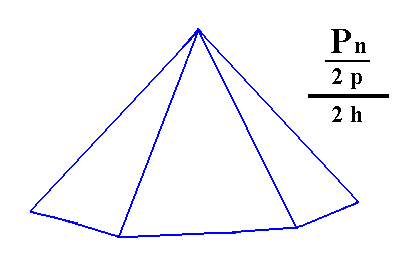 |
Figure 10. A hemimorphous pyramidal hemihedric Type III Hexagonal Monopyramid, derived from the white faces of the bipyramid of Figure 9. A similar pyramid, with its apex down, can be generated from the red faces of the bipyramid of Figure 9. |
Applying hemimorphy to the pyramidal hemihedric type I hexagonal prism results in a hemimorphous pyramidal hemihedric type I hexagonal prism, i.e. with respect to just its shape nothing happens when the equatorial mirror plane is removed. See Figure 11.
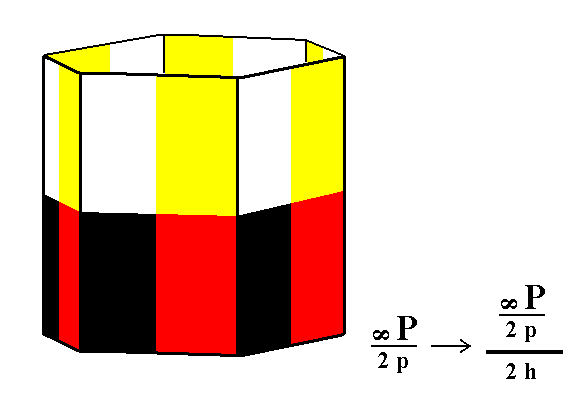
Figure 11. Generation (derivation) of the hemimorphous pyramidal hemihedric Type I Hexagonal Prism from the pyramidal hemihedric Type I Hexagonal Prism. Although its shape does not change, its symmetry is lowered, by loosing the equatorial mirror plane.
Applying hemimorphy to the pyramidal hemihedric type II hexagonal prism yields a hemimorphous pyramidal hemihedric type II hexagonal prism. Also in this case the external shape remains the same, but the symmetry is lowered. See Figure 12.
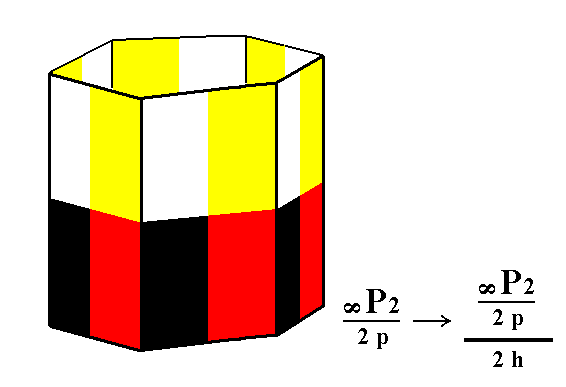
Figure 12. Generation of the hemimorphous pyramidal hemihedric Type II Hexagonal Prism from the pyramidal hemihedric Type II Hexagonal Prism.
Applying hemimorphy to the pyramidal hemihedric hexagonal tritoprism (= type III hexagonal prism) yields a hemimorphous pyramidal hemihedric type III hexagonal prism. Also here there is no change in outer shape, but there is lowering of symmetry, because of the removal of the equatorial mirror plane. See Figure 13.
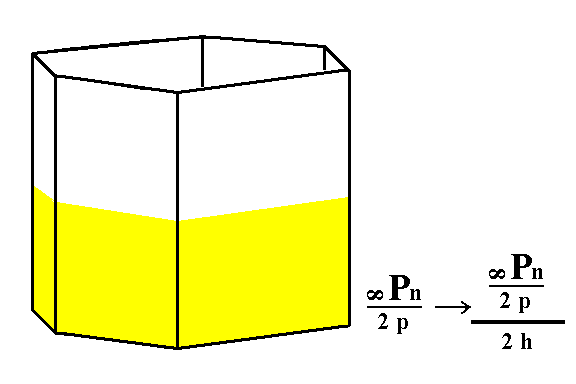
Figure 13. Generation of the hemimorphous pyramidal hemihedric Tritoprism (= hemimorphous pyramidal hemihedric Type III Hexagonal Prism) from the pyramidal hemihedric Type III Hexagonal Prism.
From the pyramidal hemihedric basic pinacoid is derived the hemimorphous pyramidal hemihedric pedion by applying hemimorphy. By dropping its equatorial mirror plane the basic pinacoid is dissolved into two independent halves, an upper and a lower one, i.e. an upper pedion and a lower pedion. So a pedion is a Form consisting of just one (horizontal) face. In combining with a hemimorphous pyramidal hemihedric prism it can close that prism at its bottom or at its top. Two pedions can close it at its top and bottom. See Figure 14 and 15.
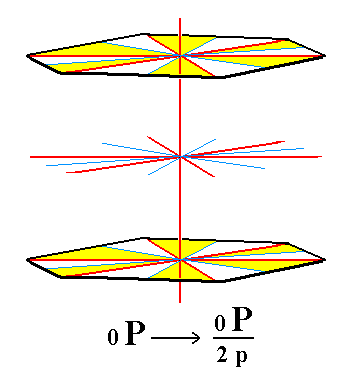 |
Figure 14. The pyramidal hemihedric Basic Pinacoid is derived from the holohedric Basic Pinacoid and supplies the Form from which we will derive the Pedion by applying hemimorphy (See Figure 15). |
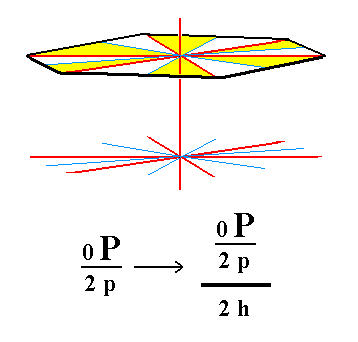 |
Figure 15. The hemimorphous pyramidal hemihedric upper Pedion is derived from the pyramidal hemihedric Basic Pinacoid by suppression of its lower halve in virtue of the removal of the equatorial mirror plane. In an analogous way a lower pedion can be derived. |
All these Forms can engage in combinations in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Hexagonal-pyramidal Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :
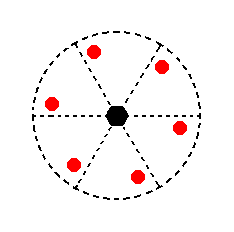 |
Figure 16. Stereogram of the symmetry elements of the Hexagonal-pyramidal Crystal Class, and of all the faces of the most general Form. |
The face a : ~a : -a : c will give rise to the Type I hexagonal monopyramid by subjecting it to all the symmetry elements of the present Class, which here means subjecting it to the workings of the 6-fold rotation axis (as the only symmetry element of the Class) coinciding with the crystallographic main axis, i.e. with the vertical axis, the c axis. This rotation axis multiplies the face six times around it and so generates a hexagonal monopyramid. See Figure 17.
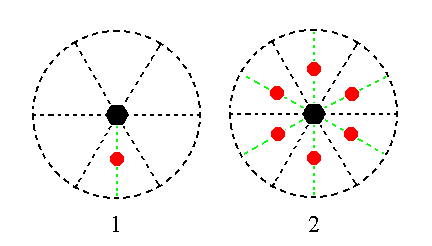
Figure 17. (1). Position of the face a : ~a : -a : c in the stereographic projection of the symmetry elements of the Hexagonal_pyramidal Crystal Class. (2). Generation -- depicting in stereographic projection -- of the Type I Hexagonal Monopyramid, by subjecting the face to the symmetry elements of the Class.
The face 2a : 2a : -a : c will give rise to a type II hexagonal monopyramid when it is subjected to the action of the 6-fold rotation axis : the face will be multiplied six times around that axis, resulting in a hexagonal monopyramid. See Figure 18.
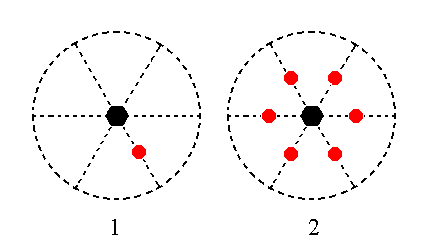
Figure 18. (1). Position of the face 2a : 2a : -a : c in the stereographic projection of the symmetry elements of the Hexagonal-pyramidal Crystal Class. (2). Stereogram of the Type II Hexagonal Monopyramid.
The face [3/2]a : 3a : -a : c is a definite face. I will treat however its generalized version, namely the face [s/(s-1)]a : sa : -a : c. Its position in the stereographic projection is a general position (i.e. it does not lie on a special location, especially not on a symmetry element, nor having a special orientation with respect to the crystallographic axes, for example being parallel to one of them or having equal intercepts with respect to two of them, like the two faces mentioned above (respectively)).
The position of that face and the generation of the Form is depicted stereographically in Figure 19. Again the Form is generated by subjecting the face to the workings of the 6-fold rotation axis, resulting in a type III hexagonal monopyramid (hexagonal tritopyramid).
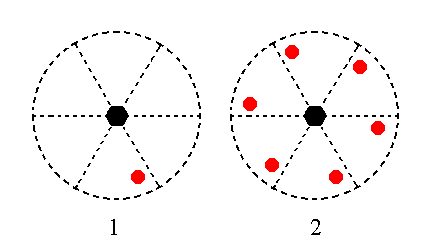
Figure 19. (1). Position of the face [s/(s-1)]a : sa : -a : c in the stereographic projection of the symmetry elements of the Hexagonal-pyramidal Crystal Class. (2). Stereogram of the generated Type III Hexagonal Monopyramid.
The face [3/2]a : 3a : -a : ~c is a definite face. We will again here treat of its generalized version, namely the face [s/(s-1)]a : sa : -a : ~c. Its orientation with respect to the horizontal crystallographic axes is the same as that of the foregoing face. It differs however in its orientation with respect to the vertical axis. It is parallel to that axis. The 6-fold rotation axis multiplies this face six times around it resulting in a type III hexagonal prism (hexagonal tritoprism).
The position of this face and the generation of the corresponding Form is depicted stereographically in Figure 20.
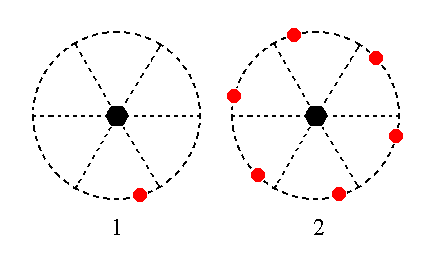
Figure 20. (1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-pyramidal Crystal Class. (2). Stereogram of the generated Type III Hexagonal Monopyramid.
The face a : ~a : -a : ~c is also vertical. When it is subjected to the 6-fold rotation axis it is multiplied six times around it, yielding a type I hexagonal prism. See Figure 21.
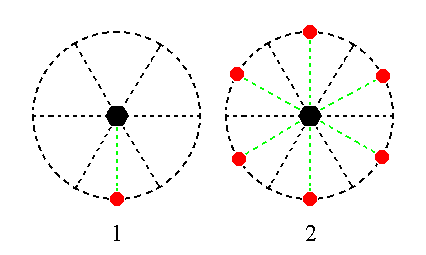
Figure 21. (1). Position of the face a : ~a : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-pyramidal Crystal Class. (2). Stereogram of the generated Type I Hexagonal Prism.
The face 2a : 2a : -a : ~c is also vertical. When subjected to the 6-fold rotation axis it is multiplied six times around it, resulting in a type II hexagonal prism. See Figure 22.
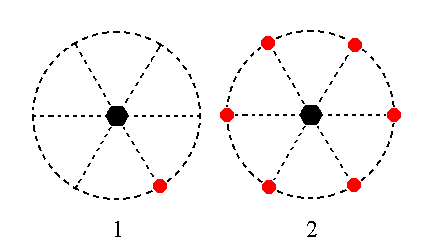
Figure 22. (1). Position of the face 2a : 2a : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-pyramidal Crystal Class. (2). Stereogram of the Type II Hexagonal Prism.
The face ~a : ~a : ~a : c is horizontal. Subjecting it to the 6-fold rotation axis does not produce new faces, so the resulting Form is that same face, a pedion. See Figure 23.
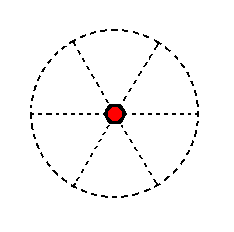 |
Figure 23. Position of the face ~a : ~a : ~a : c in the stereographic projection of the symmetry elements of the Hexagonal-pyramidal Crystal Class. The stereographic projection of the corresponding Form -- a Pedion -- is the same, because no new faces are generated. |
This concludes our exposition of the Hexagonal-pyramidal Crystal Class.
To continue, klick HERE for Part Five (Class 6 2 2).