

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Growth Rate Vector Rosette and Vector Rosette of Actual Growth
In the forgoing the Growth Rate Vector Rosette appears to indicate neatly the intrinsic shape of the crystal and its promorphological features. However, it turns out that this is not generally so. In order to express features of intrinsic shape and (some possible features) of promorphology we must not look to the Growth Rate Vector Rosette, but to a vector rosette that depicts the actually accomplished growth in a fully developed crystal, a rosette that we can call the Vector Rossette of Actual Growth. This latter rosette is a natural consequence of the Growth Rate Vector Rosette. Let us explain all this.
In the next four Figures (12m, 12n, 12o, 12p) we will construct the 2-D crystal of Figure 6 of the previous document , assuming that the chemical constitution is such that the C-faces grow fastest, then the A-faces, then the B-faces (For these faces, see Figure 3 of previous document ).
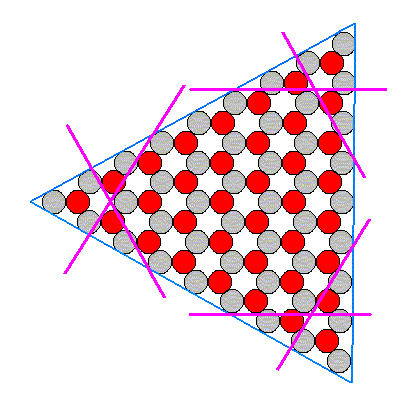
Figure 1. Construction (form evolution) of a 2-D ionic crystal, in which the C-faces grow fastest (and they have already disappeared), then the A-faces, then the B-faces . The purple lines indicate A-faces (See Figure 3 of previous document ).
Figure 2. Intermediate result of the construction of the 2-D ionic crystal.
If the growth rates of the A-faces and the B-faces were equal, then the crystal depicted in the present Figure would represent a final (form) stage.
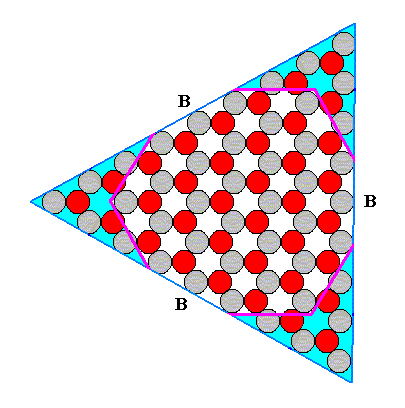
Figure 3. Continued growth of the A-faces till they disappear (as a result of their surface becoming smaller and smaller).
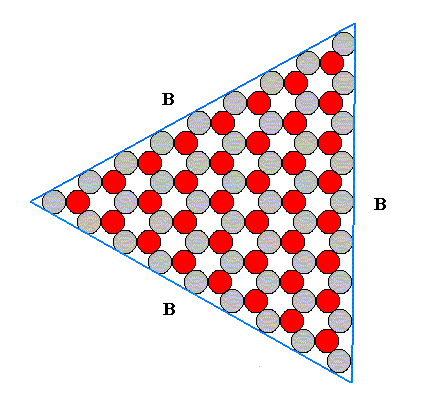
Figure 4. Final result of the construction of the 2-D ionic crystal. The A-faces have disappeared. We have a 2-D crystal bounded by three B-faces .
Next we will construct this same 2-D crystal, but now supposing that the A-faces grow fastest, then the C-faces, then the B-faces (For these faces, see Figure 3 of previous document ).
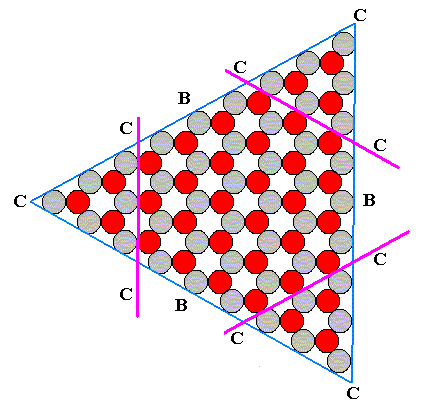
Figure 5. Construction (form evolution) of the 2-D crystal of Figure 6 of previous document , assuming now that the A-faces grow fastest, then the C-faces , then the B-faces . Purple lines indicate the growing C-faces . The A-faces have already disappeared.
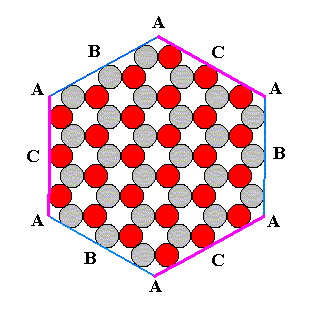
Figure 6. Intermediate phase of the construction of the 2-D crystal of Figure 6 of previous document . The A-faces have disappeared, while the C-faces continue to grow (i.e. new layers of ions are still being deposited). Compare with Figure 2 . If the B-faces were to grow exactly as fast as the C-faces , the crystal depicted here would represent already a final (form) stage.
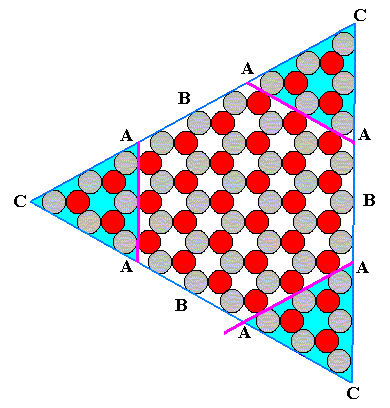
Figure 7. Final phase of the construction of the 2-D crystal of Figure 6 of previous document . The C-faces have disappeared (during growth their surface was diminishing up to its disappearance altogether), and the resulting crystal consists of the three B-faces . See next Figure.

Figure 8. Final result of the construction of the 2-D crystal of Figure 6 of previous document .
If we now add the (alleged) Growth Rate Vector Rosette of the 2-D crystal of Figure 6 of previous document in our drawing, we get the following :
Figure 9. (Alleged) Growth Rate Vector Rosette of the above constructed 2-D crystal.
Inspecting the above Figure, we can note the following :
Figure 10. True Growth Rate Vector Rosette of the above constructed 2-D crystal in the case of the A-faces growing fastest, then the C-faces , then the B-faces .
The geometry of the lattice, and the chemical nature of the motifs, of a given crystal, together determine the atomic aspects (s.l.) presented by the growing crystal to the nutrient environment, i.e. aspects along (the fronts representing) possible crystal faces. These aspects can vary with the orientation of the growing face. And they in turn determine the relative growth rates in directions perpendicular to those possible faces ( In the case of 2-D crystals having a symmetry according to the plane group P3m1 (point group 3m, or, equivalently, D3 ) these possible faces are indicated in Figure 2 of previous document ) while assuming uniform growth conditions. In this way a Growth Rate Vector Rosette results, as we have seen, for example, in Figure 10 . This Growth Rate Vector Rosette determines which possible faces will finally disappear, and thus determines the intrinsic shape of the crystal (and also the shapes of the intermediate growth stages) ( The fastest faces disappear, but this only happens when the adjacent slower growing faces taper toward each other, resulting in the diminishing of the surface of the fast growing face till that surface disappears altogether).
The presently discussed rosette consists of vectors , and a vector is just a magnitude and a direction, i.e. a vector is just a mathematical object. As such the rosette will, in the next section, be related to Promorphology (which also is mathematical in nature). But in a later document, namely Part XXIX Sequel-15 , we will relate the rosette (Vector Rosette of Actual Growth) to the shape-generating forces ('molethynes') present in a growing crystal. These forces, which are intrinsic to the given crystal, physically determine the (intrinsic) shape of the crystal. And from Part XXX onwards we will return to this rosette and again relating it to Promorphology.
Relation of Vector Rosette of Actual Growth to Antimers
A fully developed crystal has a definite number of corners. Seen from the crystal's center, these corners evidently represent definite directions (expressing the crystal's anisotropy). The rate of change of the distance from the crystal's surface to its center (this distance representing actually accomplished growth in the corresponding direction), changes abruptly at the crystal's corners. So the growth directions associated with these corners form a set of special directions within the crystal. And it is not unreasonable to assume that these special directions somehow reflect corresponding features in the chemical motif as the latter is obtained after elimination of all translational elements of the crystal, and that means that they are somehow bound up with the crystal's promorph. That this being bound up is not of a purely geometric nature only, is to be expected : chemical features also enter this relationship. This is, for instance, evident from the fact that the number of those special directions (lines to corners), that are visible when we look along the direction of the crystal's main axis, is not directly equal to the number of (microscopic) antimers, as we can see in hemi- or tetartohedric crystals (i.e. crystals, where the outer shape displays a higher symmetry than the crystal actually possesses). The number of antimers is then respectively half that number or a quarter of it. But all in all we have now established at least some connection between the Vector Rosette of Actual Growth and the crystal's antimers, i.e. between the number of directions of accomplished growth toward the corners of the crystal and the number of its (microscopic) antimers, and in turn this means that we have found some (sort of) relationship between the crystal's intrinsic shape and its promorph.
The Vector Rosette of Actual Growth must in some way be an implication (i.e. an effect) of the number and arrangement of the crystal's antimers in the (microscopic) chemical motif. This number and arrangement of antimers define such a motif and influence the way that it is repeated by translations, and so influence the crystal's shape (described by the rosette). However, the link between the latter and the number and arrangement of antimers is only indirect. A Vector Rosette of Actual Growth does not fix (in the process of reasoning from rosette to antimers) this number and arrangement. Various different patterns of antimers can, apparently, effect a same crystal shape, say that of a rectangle. To what extent the vectors of the Vector Rosette of Actual Growth reflect the number and arrangement of the crystal's antimers is dependent on the equivalence or non-equivalence of those vectors, i.e. on the nature of their surroundings.
In fact we're dealing with the following problem : At the end of Second Part of Website (and there the Section) : Basic Forms of Crystals (Especially the three concluding documents Promorphology of Crystals I, II, III ), we established the promorph of a crystal on the basis of the geometry of its microscopic motif (translation-free residue). So, in this way the promorph of a crystal (in contradistinction to that of an organism) is only microscopically expressed. Is it also at the same time in some way macroscopically expressed? The mentioned Vector Rosette of Actual Growth is, as has been said, at least some indication that the promorph of a crystal is indeed (also) macroscopically expressed. And in addition to this indication we could consider the following : The intrinsic point symmetry of the microscopic motif (as translation-free residue) is indeed macroscopically expressed, namely by the point symmetry (reflecting the Crystal Class) of the crystal as a whole, which can be determined by the inspection of the arrangement of its faces and supplemented by an inspection of the qualitative nature of these faces (etch figures, presence of striae, etc.). On the basis of this it could at least be expected that also the motif's promorph is, in addition to microscopically, in some way macroscopically expressed. In the diagrams to come (when considering examples of the relation between shape, symmetry and promorph) we 'express this being so expressed' of the promorph by explicitly drawing the macroscopical antimers (which determine the promorph) of the crystals (where we use two-dimensional crystals, for symplicity's sake).
Shape, Point symmetry, Motif and Stereometric Basic Form (Promorph).
The intrinsic internal structure of a real crystal is causally-dynamically determined by the relevant physically (including chemically) interpreted dynamical crystallization law.
For melts (i.e. molten material) this law starts to operate when certain thermodynamic conditions (temperature and pressure) prevail, causing the melt to become unstable, and sustaining crystal embryos to exist, which are then seeds for the ensuing crystallization. All this embodies the physical interpretation of the (mathematical) dynamical law.
For solutions (in solvents) the crystallization law starts to operate when, in conjunction with thermodynamic conditions (mainly temperature), certain concentration conditions are met, causing the solution to become unstable, and when seeds are present. Also this is in fact the mathematical dynamical law in a condition of physical interpretation.
In both cases (melt and solution) the physically interpreted dynamical law is a nexus category or (equivalently) a dynamical If / Then constant (as explained in Part One of the present Series of documents). It determines the trajectory leading from the initial state to a macroscopic crystal individual. So far so good with respect to the causal-dynamical determination of crystal structure.
In addition to causal-dynamical determination there is also a determination operating in another dimension, viz. the eidetical determination, i.e. determination by whatness categories or, equivalently, eidetical If / Then constants (Static If / Then constants, also explained in Part One, where also two other kinds of static If / Then constants are considered). The mentioned internal structure of a crystal is therefore also eidetically determined as to w h a t the given crystal is. It is that same dynamical law, mentioned above, that also, and at the same time, represents an eidetical If / Then constant (whatness category) with respect to the crystal it generates. It covers the whole whatness of that given crystal, i.e. it involves all its intrinsic features. It covers a complex whatness. While the dynamic crystallization law generates the crystal, namely in constituting nexus (plural) between dynamical states, the crystal's intrinsic properties are co-generated. From these intrinsic properties we have chosen to study : intrinsic shape, intrinsic symmetry (translational and non-translational), and stereometric basic form, or, equivalently, promorph, and we will investigate how they are connected and integrated in the web of determinative threads that are spun within the whole system of layers, viz. the mathematical, physical, organic, psychic and super-psychic layers (See for an introduction into such a theory of layers, Part One ). Eidetical determination of single properties, in our case shape, symmetry or promorph, is an implication emanating from such a property as analysed, to that same property as unanalysed, i.e. the latter is determined as to its whatness.
The crystal's internal symmetry structure (as an aspect of its total internal structure) can be seen as being eidetically determined by its lattice (prescribing the mode of periodic repetitiveness within the crystal) provided with chemical motifs, where, with respect to the mentioned internal symmetry, only their (point) symmetry matters, and not the additional geometric and structural features of these motifs. This lattice plus symmetry representatives of the chemical motifs constitute the crystal's Space Group (and for two-dimensional crystals we have their Plane Groups). Such a space or plane group is then a set of symmetry transformations that forms a definite algebraic structure under the operation of combining those symmetry transformations, a structure which is called a group. When we now (conceptually) eliminate all translational elements (i.e. eliminate all translations, wherever they occur in the crystal) from this Space Group (or from the Plane Group, in the 2-D case) we end up with the translation-free residue, the symmetry of which is then the crystal's Point Group. The latter is the eidetical If / Then constant (whatness determinant, whatness category) determining what the intrinsic (non-translational) symmetry, as it happens to occur in the crystal, in itself is. This Point Group thus eidetically determines the intrinsic symmetry of the (single) crystal-as-a-macroscopic (non-translational) object (because all translations -- which are by themselves microscopic -- are eliminated). And this symmetry of the crystal reflects the symmetry of the microscopic chemical motif that remains after all translations are eliminated. So we can let represent the crystal's intrinsic point symmetry by a macroscopic motif having this same (point) symmetry. This symmetry very often does not coincide with the s h a p e of the given crystal, even not with its intrinsic shape that results from a crystal being fully developed within uniform conditions. So in order to express these features conveniently, we can insert the appropriate macroscopic motif into a drawing of the intrinsic shape of a given crystal species. While the symmetry of this motif expresses the crystal's intrinsic point symmetry, the morphology of this motif (together with its symmetry) determines the promorph, i.e. it determines the number of antimers. Recall that in many cases a given definite (point) symmetry can allow for several different promorphs to be possible.
So in the diagrams of 2-D crystals (next document) we will depict the following items :
The next two Figures give some examples of "inserted macroscopic motifs" and their symmetry.
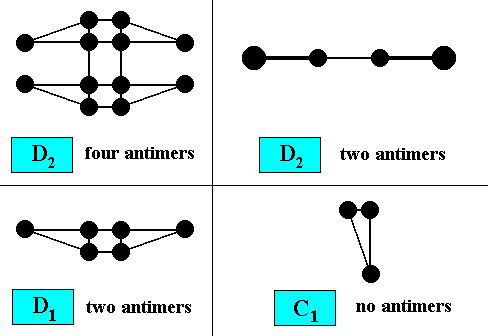
Figure 11. Possible two-dimensional motifs of two-dimensional crystals.
The symmetry of a macroscopical version of such a motif, inserted in a drawing of a crystal shape, can indicate the crystal's intrinsic point symmetry. The morphology of the motif allows for the crystal's promorph to be assessed, because it shows the number and arrangement of antimers. The next Figure illustrates the symmetry of those motifs, which are according to the groups D2 , D1 and C1 .
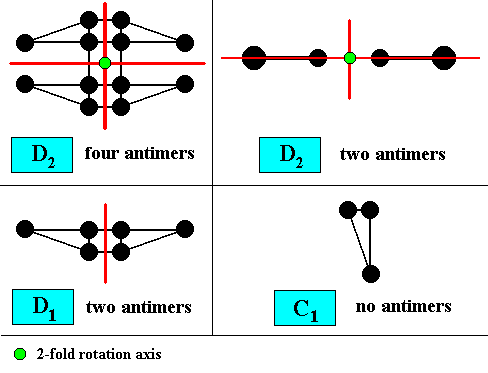
Figure 12. Symmetry of the two-dimensional motifs of the Figure above. Mirror lines indicated by red lines. Two-fold rotation axis indicated by a small solid green circle. The C1 motif does not have any symmetry at all besides the trivial symmetry transformation : 00 or, equivalently, 3600 rotation about any axis.
Shapes of Two-dimensional Crystals and Crystallographic Forms
Crystals (in our case, 2-D crystals) are bounded by possible faces. Possible crystal faces are either parallel to the edges of the unit mesh (which is that microscopic unit that is repeated periodically), or follow oblique stacking boundaries, such as indicated in the next Figure :
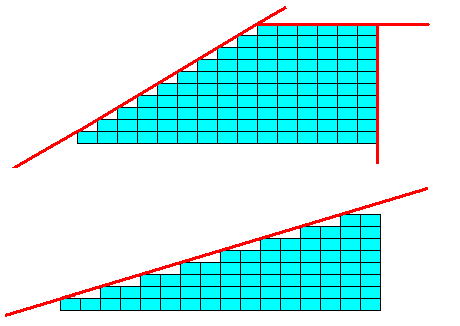
Figure 13. Possible faces (red) of a 2-D crystal with rectangular building blocks (unit meshes).
As has been explained earlier, the total set of crystal faces present on a given crystal is constituted by one or more Forms in the crystallographic sense. Recall that such a Form originates as follows : If we suppose one of the possible faces to be present, then the presence of copies of this face can automatically be expected, depending on the intrinsic point symmetry of the crystal and on the position of this face with respect to the symmetry elements (in 2-D crystals, reflection lines and/or rotation axes) of the crystal. When this produces a closed figure it could be a crystal. If only an open Form is produced (for instance two parallel lines and nothing more), then such a Form must be combined with one or more other Forms in order to represent a crystal. So the shape of a crystal consists of one or more stronger or weaker (i.e. prominent or not so) developed crystallographic Forms. In this way a rectangular 2-D crystal could consist of four, three, or two Forms, depending on the intrinsic point symmetry of the crystal, i.e. on its Crystal Class. In the ensuing series of diagrams we will indicate the crystallographic Forms involved in making up a given intrinsic shape of some 2-D crystal.
Crystals and Organisms
It is especially the promorph that eidetically connects crystals and organisms by determinative threads. Apart from symmetry, the promorph relates to purely morphological features, often not accounted for by symmetry alone : The number of antimers is generally not determined by symmetry alone, but also by conspicuous morphological features. The intention of this and the following documents indeed is to bring crystals and organisms together as far as possible, realizing, of course, that they have only a limited set of features in common. Crystals are periodic structures based on certain lattices, and although it is perhaps possible to suppose such lattices also to be present in certain organismic types, it is far from certain. An organic lattice could be present in the form of some chemical system (something like a Turing pattern) that provides for "position information" in a developing organism, it is true, but in many other cases, like in spiral organisms, it cannot be as such present. Often the regular spatial structure of organismic bodies is determined by certain stable and robust dynamical subsystems operating during morphogenesis without the necessity of some pre-existing or pre-generated organic lattice, as for instance in the phyllotaxis of plants, where leaf distribution in the growing plant is accomplished by a simple robust dynamic of repulsion of leaf primordia, resulting in the overall symmetry and promorph of the plant in the form of discrete spirals leading to a basic form that is somehow intermediate between Spiraxonia (continuous spirals) and Stauraxonia (pyramids and bipyramids) [See for a System of these promorphological categories our System of Basic Forms in Second Part of Website ].
A general pattern theory will connect crystals and organisms by determinative whatness categories, and in this way connect the Mathematical Layer on the one hand, with the Physical and Organic Layers on the other, which are otherwise separated by a huge complexity gap ( The latter already exists between the Physical [i.e. Inorganic] Layer and the Organic Layer, but is especially prominent between the Mathematical Layer and the Non-mathematical Layers [and therefore Temporal Layers], i.e. between the Ideal Sphere s.str. of Existence and the Real Sphere s.str. of Existence [See for this Part One] ).
Promorphs as whatness categories
Here we repeat, from Part I, a section on the ontology and essence of promorphs or basic forms, in order to clearly understand what promorphs in fact are, and especially what they are as co-determinants of the overall spatial structure of crystals and organisms.
Intrinsic symmetry is one of the aspects of the structure of a being. The promorph is also such an aspect. It presupposes intrinsic point symmetry, and is in many cases equivalent to it (apart from the fact that it involves exclusively geometric and dimensional aspects of structure), while in other cases the promorph goes beyond symmetry, especially in all cases where the number of antimers (counterparts of a body) is not fixed by symmetry alone. So like symmetry the promorph is an intrinsic property which is implied by the Essence of the given being and is as such part of that being's whatness.
We can say that an object (where we always mean an intrinsic being) has or has not symmetry. And only when we consider the trivial group C1 to be a symmetry as well, we can say that every object has (a certain) symmetry, or, equivalently, is symmetric.
In the same way we can say that an object has or has not a promorph. And only if we consider completely irregular bodies, namely bodies that do not possess a definite geometric body center, nor repeating parts, nor similar or homologous parts, as having a promorph as well, i.e. if we consider the Anaxonia acentra of our Promorphological System to represent a promorph as well, then we can say that every object has a promorph, or, equivalently, is promorphic. If, on the other hand, we do not so consider, then all promorphic bodies, and only promorphic bodies, show a definite pattern of polarities with respect to their axes, as well as to all other parts of their overall structure.
A body axis can be either homopolar, which means that both ends of that axis represent (or are embedded within) equal or similar body parts, or heteropolar, which means that one end of that axis represents a body part unequal to the body part represented by the other end of that axis ( Think of head---tail as representing a heteropolar axis of the body of many an animal). As with axes, these polarity features can also be present in other structural elements of a body. It is possible to express these polarities in a geometric way, and this is what Promorphology is doing, it finds the simplest geometric bodies or figures that fully express these polarities geometrically, which is equivalent to geometrically express the intrinsic point symmetry of the object and the number and arrangement of its antimers (See for Promorphology, Second Part of Website , Main Section Basic Forms (Promorphological System)).
So in line with the Category of Symmetry, we can establish the Category of Promorphology and the corresponding more special promorphological categories (Recall that categories are If / Then constants, and are, consequently, expressed in an ontological fashion, i.e. as determinants, and not as logical definitions) :
Category of Promorphology (whatness category) :
If an object possesses at least a geometric body center, or allows for certain definite body axes, then it is promorphic.The concretum of this category is all beings (objects) that are promorphic, but more strictly it is promorphic as unanalysed.
[If we consider the Anaxonia acentra to be a promorph as well, then all beings are promorphic.]
The corresponding logical definition would run as follows :
An object is called promorphic if it contains at least a geometric body center, or allows for certain definite body axes.
The logical and ontological expressions are logically equivalent, but the logical definition is not a category.
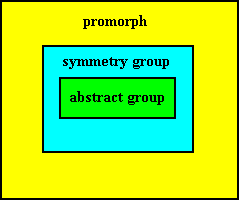
General Category of Promorph (whatness category) :
If a given being (object) is promorphic, then its body possesses a definite pattern of polarities, not only of its body axes, but of all parts of its overall structure. This pattern is its promorph.The concretum of this category is all beings (objects) that have a promorph, but more strictly it is promorph as unanalysed.
Although these two categories, viz. the Category of Promorphology and the General Category of Promorph, are more or less equivalent, it is contributing to clarity if we present them separately.
A promorph, or, equivalently, a stereometric basic form (for 3-D space) or planimetric basic form (for 2-D space), implies and contains the corresponding symmetry group, while the latter in turn implies and contains the corresponding abstract group.
See for symmetry group and abstract group The Intermezzo of Part XIII of the Series Subpatterns and Subgroups in
Second Part of Website .
Click H E R E to see this Intermezzo in a separate window (To leave it again, close the window).
To actually go there, click the just given Second Part of Website link, then scroll the left frame through the Series on Group Theory, then click on "SEQUEL TO GROUP THEORY two-dimensional patterns", and then, finally, click on Part XIII of the Series on Subpatterns and Subgroups and scroll down to INTERMEZZO.
So the structure of the General Category of Promorph can be visualized as follows :
The following is a statement that is wholly equivalent to that of the General Category of Promorph , but is as such not ontologically meant, but methodologically :
A promorph is the simplest geometric solid expressing the intrinsic point symmetry of a given being and the number and arrangement of that being's bodily counterparts (antimers). This simple geometric solid directly depicts the polarity pattern of that given being.
In the exposition of the special categories of promorphs we will use this methodological definition, while nevertheless interpreting it o n t o l o g i c a l l y, i.e. m e a n i n g it according to the content of the above General Category of Promorph .
So let us then give a special promorphology category :
Category of Allopolar Pentamphipleural Promorph [or just, Category of Allopola pentamphipleura] (whatness category) :
If we have a promorphic being (object) of which the pattern of polarities can be expressed as half a ten-sided amphitect pyramid (and in a 2-D case : as half a ten-sided polygon), then the promorph of this being is that of the Allopola pentamphipleura.The mentioned pyramid, viz. half a ten-sided amphitect pyramid must then be explicitly indicated :
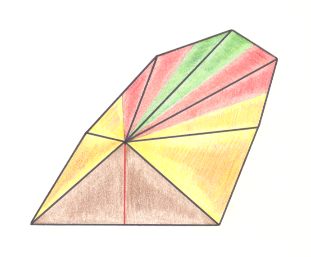
Figure 14. Oblique top view of the promorph of the bodies of, say, irregular sea urchins (Besides sea-urchins, also many flowers have this promorph). It is half a 10-fold amphitect pyramid with the five antimers (corresponding to five body parts in the animal) indicated by colors. It therefore belongs to the Pentamphipleura (Allopola amphipleura). The brown plane facing the beholder is the bisection face associated with the bisection of the 10-fold amphitect pyramid.
The concretum of this category is all beings (objects) that have this promorph, but more strictly it is this promorph as (partly) unanalysed, namely as (just) belonging to the "Allopola pentamphipleura", or just "Pentamphipleura".
The Category of Allopola pentamphipleura implies and contains the Symmetry Group D1 , and the latter in turn implies the Abstract Two-element Group.
The Abstract Two-element Group can be given by the following group table. Its elements are not in any way interpreted. They are what they are in virtue of their relations as defined in that group table :
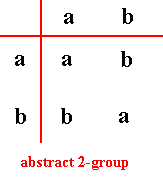
From the table it is clear that the element a is the group's identity element.
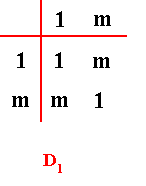
( This group D1 can itself be a whatness category, namely the Category of Bilateral Symmetry, as we defined it HERE in Part I ).
So the structure of the Category of Allopola pentamphipleura , as such a special promorph, can be visualized as follows :
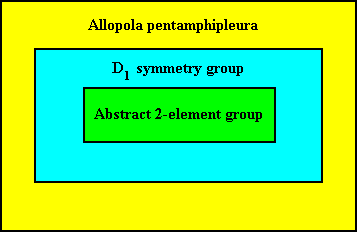
This promorph, viz. that of the Allopola pentamphipleura, which as such is just a geometric figure, involving just 3-D metric space (and not physical space), and so still being a purely mathematical entity, can now be physically interpreted, viz. inorganically or organically. We will often find it interpreted organically, as in irregular sea-urchins and in flowers of at least many Scrophulariaceae. However, this organic interpretation of the promorph does not mean just its materialization (i.e. transition of the involved space from mathematical to physical space) of the promorph : We generally don't find organisms appearing as pyramids or other such polyhedral solids.
Shape, Symmetry and Promorph, expressed in diagrams of some two-dimensional crystals.
In the following we set a certain (intrinsic) SHAPE of a two-dimensional crystal as given, such as a Rectangle, a Square, a Parallelogram, a Rhombus, an Equilateral Triangle or a Regular Hexagon, and consider its relationship with the crystal's promorph.
Before we start, we first give an overview of the mentioned possible m a i n intrinsic shapes, viz. Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon, that can be adopted by fully developed two-dimensional crystals, and how these shapes can conceptually be built by a number of (crystallographic) Forms.

| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 4 |
| P2 | C2 ( 2 ) | 2 |
| Pm Cm Pg |
D1 ( m ) | 3 |
| P2mm C2mm P2mg P2gg |
D2 ( 2mm ) | 2 |

| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 4 |
| P2 | C2 ( 2 ) | 2 |
| Pm Cm Pg |
D1 ( m ) | 2 |
| P2mm C2mm P2mg P2gg |
D2 ( 2mm ) | 1 |
| P4 | C4 ( 4 ) | 1 |
| P4mm P4gm |
D4 ( 4mm ) | 1 |

| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 4 |
| P2 | C2 ( 2 ) | 2 |

| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 4 |
| P2 | C2 ( 2 ) | 2 |
| Pm Cm Pg |
D1 ( m ) | 2 |
| P2mm C2mm P2mg P2gg |
D2 ( 2mm ) | 1 |
| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 3 |
| Pm Cm Pg |
D1 ( m ) | 2 |
| P3 | C3 ( 3 ) | 1 |
| P3m1 | D3 ( 3m ) | 1 |
* The plane group P31m does not support regularly-triangular crystals, as we will see in the sequel.

| Plane Group | Point Symmetry | Number of Forms |
| P1 | C1 ( 1 ) | 6 |
| P2 | C2 ( 2 ) | 3 |
| Pm Cm Pg |
D1 ( m ) | 3 |
| P2mm C2mm P2mg P2gg |
D2 ( 2mm ) | 2 |
| P3 | C3 ( 3 ) | 2 |
| P3m1 P31m |
D3 ( 3m ) | 1 |
| P6 | C6 ( 6 ) | 1 |
| P6mm | D6 ( 6mm ) | 1 |
We will now discuss the mentioned shapes one by one (rectangle, square, parallelogram, rhombus, equilateral triangle, regular hexagon) as outlined above. But before doing that, first some explanations of promorphological names used in the sequel are given (but for full details see Second Part of Website (and there) at : BASIC FORMS ) :
Axonia :
In three dimensions : Bodies with one or more fixed axes.
In two dimensions : Figures with one or more fixed axes.
Stauraxonia :
In three dimensions : Pyramidal forms (pyramids and bipyramids, regular or irregular). Cylinders, Cones, and the like, do not belong to the Stauraxonia.
In two dimensions : Polygons (regular or irregular). Circles do not belong to the Stauraxonia.
Stauraxonia homostaura :
In three dimensions : Regular single pyramids (Stauraxonia Heteropola homostaura).
In two dimensions : Regular polygons (Stauraxonia homostaura).
Homostaura anisopola :
Homostaura with unequipolar cross axes.
Homostaura isopola :
Homostaura with equipolar cross axes.
Homostaura (anisopola) triactinota :
Homostaura with three antimers :
In three dimensions : regular 3-fold single pyramids.
In two dimensions : Equilateral triangles.
Homostaura (isopola) tetractinota :
Homostaura with four antimers :
In three dimensions : regular 4-fold single pyramids, i.e. quadratic single pyramids.
In two dimensions : Squares.
Homostaura (anisopola) pentactinota :
Homostaura with five antimers :
In three dimensions : regular 5-fold single pyramids.
In two dimensions : Regular pentagons.
Homostaura (isopola) hexactinota :
Homostaura with six antimers :
In three dimensions : regular 6-fold single pyramids.
In two dimensions : Regular hexagons.
Stauraxonia heterostaura :
In three dimensions : Irregular single pyramids, either whole flattened pyramids (amphitect pyramids), or one half of such a pyramid, or one quarter of such a pyramid.
In two dimensions : Irregular polygons, either whole flattened polygons (amphitect polygons), or one half of such a polygon, or one quarter of such a polygon.
Heterostaura autopola :
In three dimensions : whole amphitect pyramids.
In two dimensions : whole amphitect polygons.
Autopola orthostaura :
Autopola with two or four antimers, implying that the number of radial cross axes is maximally two, and these are then intersecting at right angles. If, however, in Autopola with four antimers, viz. the Autopola tetraphragma, the four antimers are arranged such that the directional axes (i.e. the two cross axes that intersect at right angles) are interradial (i.e. not coinciding with the median lines of the antimers), as in the Autopola tetraphragma interradialia, the two radial cross axes intersect at acute angles. This is the case with rectangular pyramids (three dimensions) and rectangles (two dimensions) with four antimers. And because the symmetry of such a rectangular pyramid or rectangle is the same as a rhombic pyramid or rhombus with four antimers, where indeed the radial cross axes meet at right angles, implying them to be true Autopola orthostaura, and because the rhombus is a more simpler figure then a rectangle, we still consider the latter, viz. rectangular pyramid an rectangle, to be orthostaura as well. In the case of Autopola with only two antimers, there are only two cross axes, one radial, one interradial, and these meet at right angles (Autopola Orthostaura diphragma). In the drawings of the geometric figures representing the Autopola (Autopola Tetraphragma radialia, Autopola Tetraphragma interradialia, Autopola diphragma, Autopola hexaphragma, etc.) this all will become clear.
Autopola oxystaura :
Autopola with 6, 8, 10, 12, . . . antimers, implying that the number of radial cross axes is minimally three, and these are then generally intersecting at acute angles.
Autopola (orthostaura) diphragma :
Autopola with two antimers.
Autopola (orthostaura) tetraphragma :
Autopola with four antimers.
Autopola (oxystaura) hexaphragma :
Autopola with six antimers.
Autopola (oxystaura) octophragma :
Autopola with eight antimers.
Heterostaura allopola :
In three dimensions : half- or quarter-amphitect pyramids (bilateral forms s.l.).
In two dimensions : half-or quarter-amphitect polygons (bilateral forms s.l.).
Allopola zygopleura :
Allopola with two or four antimers.
Zygopleura eutetrapleura :
Symmetric Zygopleura with four antimers.
Zygopleura eudipleura :
Symmetric Zygopleura with two antimers (bilateral forms s.str.).
Allopola amphipleura :
Allopola with 3, 5, 6, 7, 8, . . . antimers.
Stauraxonia (listed already earlier) :
In three dimensions : Pyramidal forms (pyramids and bipyramids, regular or irregular).
In two dimensions : Polygons (regular or irregular).
Stauraxonia gyrostaura :
In three dimensions : Twisted single pyramids (flattened or not) (Stauraxonia heteropola gyrostaura).
In two dimensions : Twisted polygons (flattened or not) (Stauraxonia gyrostaura).
Gyrostaura homogyrostaura :
In three dimensions : Regular twisted single pyramids.
In two dimensions : Regular twisted polygons.
Homogyrostaura trimera :
In three dimensions : Regular twisted single pyramids with three antimers.
In two dimensions : Regular twisted polygons with three antimers.
Homogyrostaura tetramera :
In three dimensions : Regular twisted single pyramids with four antimers.
In two dimensions : Regular twisted polygons with four antimers.
Homogyrostaura pentamera :
In three dimensions : Regular twisted single pyramids with five antimers.
In two dimensions : Regular twisted polygons with five antimers.
Homogyrostaura hexamera :
In three dimensions : Regular twisted single pyramids with six antimers.
In two dimensions : Regular twisted polygons with six antimers.
Homogyrostaura heptamera :
In three dimensions : Regular twisted single pyramids with seven antimers.
In two dimensions : Regular twisted polygons with seven antimers.
Homogyrostaura octomera :
In three dimensions : Regular twisted single pyramids with eight antimers.
In two dimensions : Regular twisted polygons with eight antimers.
Gyrostaura heterogyrostaura :
In three dimensions : Amphitect twisted single pyramids.
In two dimensions : Amphitect twisted polygons.
Heterogyrostaura dimera :
In three dimensions : Amphitect twisted single pyramids with two antimers.
In two dimensions : Amphitect twisted polygons with two antimers.
Heterogyrostaura tetramera :
In three dimensions : Amphitect twisted single pyramids with four antimers.
In two dimensions : Amphitect twisted polygons with four antimers.
Heterogyrostaura hexamera :
In three dimensions : Amphitect twisted single pyramids with six antimers.
In two dimensions : Amphitect twisted polygons with six antimers.
Heterogyrostaura octomera :
In three dimensions : Amphitect twisted single pyramids with eight antimers.
In two dimensions : Amphitect twisted polygons with eight antimers.
Anaxonia :
In three dimensions : Bodies without fixed axes.
In two dimensions : Figures without fixed axes.
Rectangle
Let us consider a fully developed 2-D (i.e. two-dimensional) (imaginary) crystal having a rectangular shape :

Any rectangular crystal can be conceived as being built up by a periodic stacking of microscopic rectangular units, as the next Figure illustrates.

Its true point symmetry is either according to the Dihedral Group D2 (crystallographically indicated as 2mm ), or to the Dihedral Group D1 (crystallographically indicated as m ), or to the Cyclic Group C2 (crystallographically indicated as 2 ), or, finally, to the Asymmetric Group C1 , all depending on the crystal's internal structure.
That a rectangular crystal can have these intrinsic symmetries can be explained succinctly as follows (and will be further evident in the sequel) :
A Rectangle as such has the following symmetries, i.e. it will be superposed upon itself by the following transformations (which are then for that reason symmetry transformations) :
The above table showed which plane groups can support our main shapes under consideration (rectangle, square, parallelogram, rhombus, triangle, hexagon).
P2mm, C2mm, P2mg, P2gg, which have a point symmetry according to D2 .
Pm, Cm, Pg, which have a point symmetry according to D1 .
P2, which has a point symmetry according to C2 .
P1, which has a point symmetry according to C1 .
For each of these plane groups we will show how it supports a rectangular crystal shape. The intrinsic shape of the crystal, in the present case its rectangular shape, depends on the Growth Rate Vector Rosette, which in turn depends on the atomic aspects (chemical nature of motifs and geometry of lattice) presented to the growing environment by the possible crystal faces. The rectangular crystal can be formed by the stacking of rectangular or rhombic building blocks (unit meshes) containing a motif s.str. compatible with the point symmetry implied by the given plane group. The point symmetry is indicated in each case. Recall that the point symmetry of a crystal is the translation-free residue of its plane group symmetry.
A rectangle, which has a symmetry according to the group D2 , will be supported by those plane groups of which all the implied point symmetries (i.e. implied by the plane group) are also symmetries of the Rectangle. This does not necessarily hold the other way around : A crystal can have an intrinsic shape that is a rectangle, but nevertheless some, or even all, symmetries of this rectangle can be absent in the crystal, resulting in the fact that the intrinsic symmetry of the crystal is lower than that of its intrinsic shape.
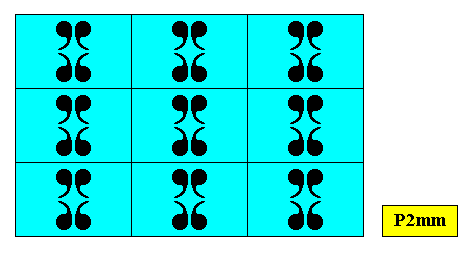
Figure above : Two-dimensional rectangular crystal, point symmetry D2 , and supported by a primitive rectangular point lattice (indicated by connection lines).
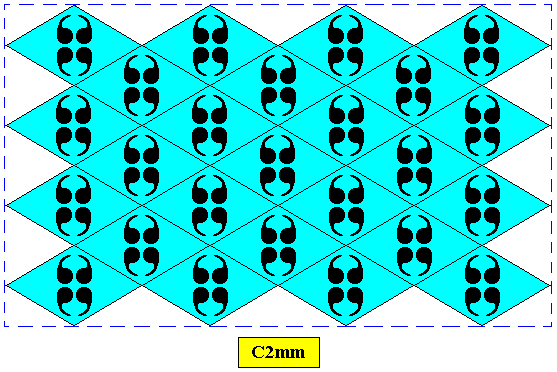
Figure above : Two-dimensional rectangular crystal, point symmetry D2 , and supported by a rhombic point lattice (indicated by connection lines).
Figure above : Two-dimensional rectangular crystal. Point symmetry D2 . It is supported by a centered rectangular point lattice (indicated by connection lines).
The next two Figures elucidate the above Figure, i.e. they elucidate some features of C2mm patterns.
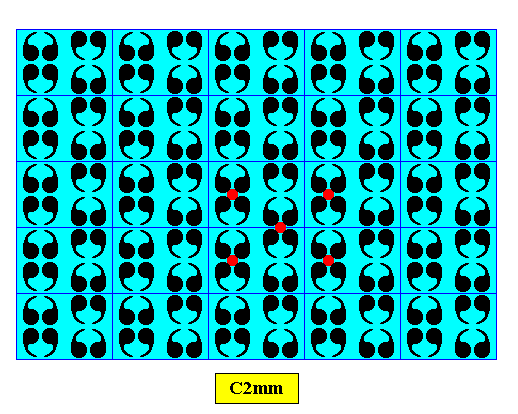
Next, the rhombic point lattice of this same pattern is indicated. It can alternatively (with respect to an equally possible centered rectangular point lattice) describe the periodic repetition of motifs :
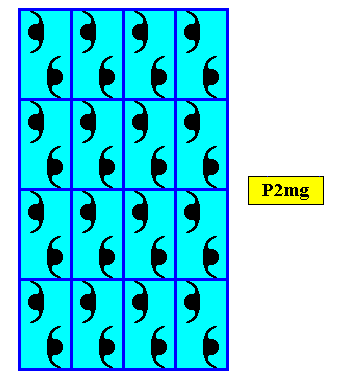
Figure above : Two-dimensional rectangular crystal, point symmetry D2 , and supported by a primitive rectangular point lattice (indicated by connection lines).

Figure above : Two-dimensional rectangular crystal, point symmetry D2 , and supported by a primitive rectangular point lattice (indicated by connection lines).

Figure above : Two-dimensional rectangular crystal. Point symmetry D1 , and supported by a primitive rectangular point lattice (indicated by connection lines).
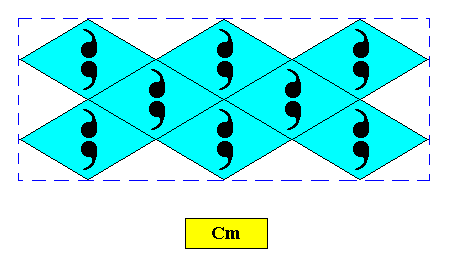
Figure above : Two-dimensional rectangular crystal, point symmetry D1 , and supported by a rhombic point lattice (indicated by connection lines).
Figure above : Two-dimensional rectangular crystal, point symmetry D1 , and supported by a centered rectangular point lattice (indicated by connection lines).
The next Figure depicts the same as the previous one. Some equivalent points are indicated. They represent the centered rectangular lattice of the pattern by which the repetition of its motifs can (also) be described.
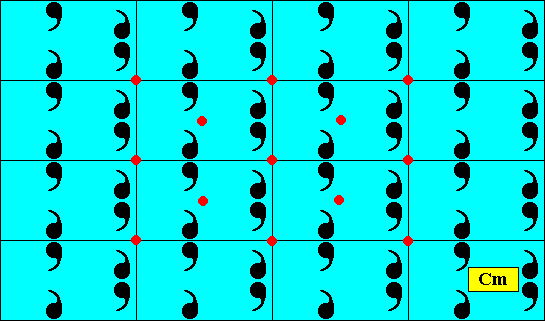

Figure above : Two-dimensional rectangular crystal, point symmetry D1 , and supported by a primitive rectangular point lattice (indicated by connection lines).
The next Figure depicts a rectangular crystal with total symmetry according to the plane group P2. The two translations by which the two-fold motifs of this pattern are repeated happen to be perpendicular to each other (because of details and chemical affinities of the motifs). Generally the translations of P2 patterns are not perpendicular to each other, resulting in an oblique lattice.

Figure above : Two-dimensional rectangular crystal, point symmetry C2 , and supported by an oblique point lattice (indicated by connection lines), where the angles happen to be 900.
The next Figure, finally, depicts a rectangular crystal with total symmetry according to the plane group P1. The two translations by which the asymmetric motifs of this pattern are repeated happen to be perpendicular to each other (because of details and chemical affinities of the motifs). Generally the translations of P1 patterns are not perpendicular to each other, resulting in an oblique lattice.

Figure above : Two-dimensional rectangular crystal, point symmetry C1 , and supported by an oblique point lattice (indicated by connection lines), where the angles happen to be 900.
This concludes a summary, showing when, and in what way, rectangular 2-D crystals are supported. As can be seen in the above Figures, in many cases the actual point symmetry of the (rectangular) crystal is lower than that of the Rectangle.
In the next document we will investigate the promorphs of these rectangular 2-D crystals.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part VI.
e-mail : 