

e-mail :

Up to now we have studied Shape, Symmetry and Promorph as representing special categories of being. We thereby have spent a great deal of effort to demonstrate their universal status. We did this by relating crystals to organisms, resulting in the Theory of Organic Lattices (Part XXIX Sequel-10 up to Part XXIX Sequel-12 ) and the working-out of the crystal analogy (Part XXIX Sequel-16 ).
The present document continues the investigation of the mentioned special categories (If / Then constants), and continues to compare crystals with organisms.
Having studied Shape, Symmetry and Promorph in two-dimensional crystals from the viewpoint of their point symmetry (translation-free residue) (Part IV--XXVIII), and having summarized and discussed the results so far obtained (Part XXIX), we will now study Shape, Symmetry and Promorph in (again) two-dimensional crystals, but now from the viewpoint of their plane group symmetry, i.e. of their total symmetry which includes translations and translational components.
In order to understand in what follows, it would be advisable to fresh up things that were discussed earlier (in Part IV and Part V), things, which could have slipped away again from the (reading) mind during the long intervening discussion on ontology, thermodynamics and crystal analogy, that separates Part V from the present Part (Part XXX). The reader should start rereading Part IV from the section Growth Rate Vector Rosette in Crystals till the end of the document, and then reread Part V till he/she arrives at the section Crystals and Organisms
Crystals and Organisms, Shape, Symmetry and Promorph.
In the triangular 2-D crystal of Figure 6 of Part IV (having the same internal symmetry as the hexagon-shaped crystal as depicted in Figure 4 of Part IV ) the atomic aspects of all the faces are, alternatively, assumed to be such that the B-faces (See Figure 2 of Part IV) have the slowest growth rate. So this crystal is chemically different from the mentioned hexagonal crystal (Probably an ionic crystal crystallizing in a hexagonal lattice admits of only one growth rate pattern. In this case we must formulate what has just been said, slightly differently : If, in virtue of the atomic aspects the respective growth rates were as indicated in Figure 12 of Part IV, then we get a crystal with a hexagonal shape. If, on the other hand, the atomic aspects of the faces of this crystal are in fact as specified in Figure 6 of Part IV or in Figure 13 of the present document, then this crystal must have a triangular shape).
In Part IV and Part V we have found out that a rosette of growth directions, drawn as originating in the center of the fully-grown crystal and terminating at the crystal's borders (corners or edges) does not unequivocally reflect the relative growth rates of possible faces of that crystal. However, the slowest growth directions are directly evident : They are perpendicular to the extant faces of such a crystal, provided that these faces could have grown themselves out of existence were they fast growing. This condition (of growing out of existence) is fulfilled when the ajacent possible slower growing faces taper in such a way that the surface of the faster growing face between them gets smaller and smaller until it finally vanishes altogether. So while the directions of the slowest growing faces can be identified by drawing lines from the crystal's center perpendicular to the extant crystal faces, the relative growth in the other directions cannot be so determined. This implies that a rosette, consisting of lines going from the crystal's center to its corners and edges, does not represent a Growth Rate Vector Rosette, but instead a Vector Rosette of Actual Growth, which thus depicts the growth that has actually taken place in the crystal, reckoned from its center in the directions of growth of actual and potential faces. In Part XXIX Sequel-15 we have associated this Vector Rosette of Actual Growth, which itself is just a mathematical entity, with the Rosette of Effective Molethynes, which represents forces (and is thus a physical entity) that determine the crystal's intrinsic shape. The next Figure depicts the Vector Rosette of Actual Growth of a triangular (imaginary) two-dimensional ionic crystal.
Figure 1. Vector Rosette of Actual Growth of the crystal of Figure 6 of Part IV. One can clearly see that the B-faces have the lowest growth rate, while either the C-faces or the A-faces have the highest.
As has been found out earlier, for a Vector Rosette of Actual Growth to be indicative for the resulting Shape of the crystal, it is sufficient to give those vectors that point to the corners, so the following Rosette will do :
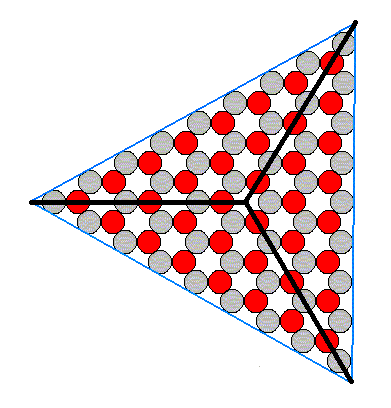
Figure 2. Vector Rosette of Actual Growth of the crystal of Figure 6 of Part IV, as indicative for the Shape of the crystal.
The next Figure indicates the radial and interradial areas of the crystal.
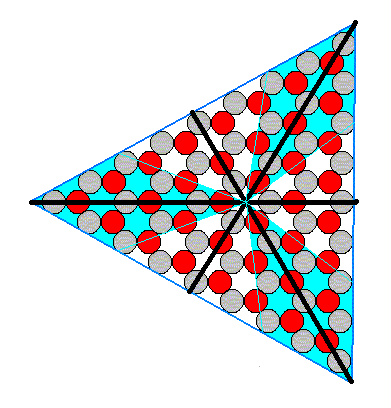
Figure 3. Radial (blue) and interradial (white) areas of the triangular ionic crystal ( The boundaries are, of course, more or less arbitrary).
The next Figure indicates the three antimers of the crystal.
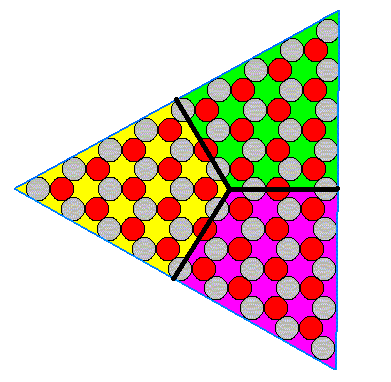
Figure 4. The three antimers of the triangularly shaped 2-D ionic crystal.
As was the case in the hexagonally shaped crystal above, the Promorph of the present crystal is again that of the Anisopola triactinota, because the motif has D3 symmetry. [ In the present case we again have to do with a two-dimensional crystal, which is an equilateral triangle. The corresponding three-fold pyramid (representing the corresponding 3-D crystal, and also its Promorph, and belonging to the Class 3m) has the same symmetry as the equilateral triangle.]. See Figure 22 of Part IV.
In the next Figure we depict the ionic crystal (still having P3m1 symmetry as before) as it would be when the atomic aspects were not as assumed in Figure 13, and also not as was assumed in Figure 12 of Part IV, but are assumed to be such that the growth rate of the C-faces is highest, as in Figure 8 of Part IV ( The C-faces have grown themselves out of existence), resulting in a truncated hexagon.
Figure 5. With respect to the ionic 2-D crystal it is assumed that the C-faces grow with the highest rate. They will ultimately disappear, resulting in a hexagon of which three corners have been cut off by a triangle formed by the B-faces. The Vector Rosette of Actual Growth is indicated.
As was established above, to determine a vector rosette of actual growth that adequately indicates the Shape of a crystal (and also of an organism), it is sufficient (and necessary) to give all (and only) those vectors that point (from the center) to the corners of the crystal ( This applies to the crystal as seen along its main axis -- if it has such an axis -- as well as to the crystal as seen perpendicular to that axis). Some of these vectors will -- as consequence -- be composed vectors : A composed growth vector is a vector that is implied by two differently directed original growth vectors perpendicular to the relevant faces.
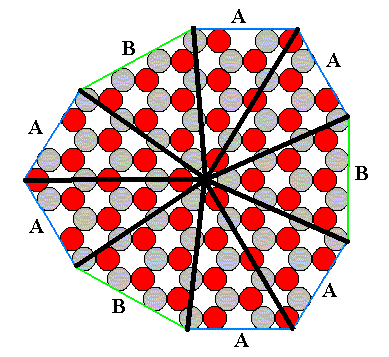
Figure 6. Final Vector Rosette of Actual Growth for the 2-D ionic crystal of Figure 8 of Part IV.
The next Figure indicates the radial and interradial areas of this truncated hexagonal crystal.
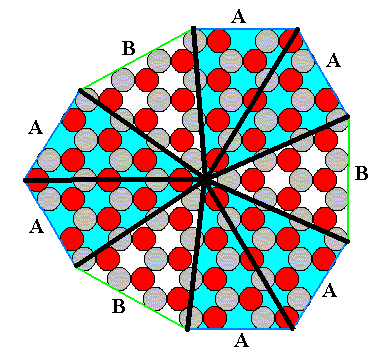
Figure 7. Radial (blue) and interradial (white) areas of the truncated hexagonal 2-D ionic crystal under discussion ( The boundaries of these areas are of course more or less arbitrary).
The three antimers of the truncated hexagonal crystal are depicted in the next Figure.
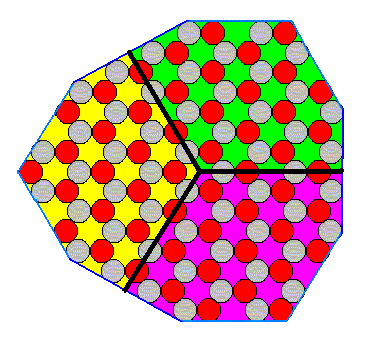
Figure 8. The three antimers of the 2-D ionic crystal of Figure 8 of Part IV.
According to Figure 8 the Promorph of this crystal can be represented by an equilateral triangle (having the same symmetry as a three-fold pyramid), and as such belongs to (a 2-D analogue of) the Anisopola triactinota of the Promorphological System. See Figure 22 of Part IV.
If the A-faces are assumed to be the fastest growing faces, the crystal must look like the one depicted in Figure 9 of Part IV, and the Vector Rosette of Actual Growth would be as follows :
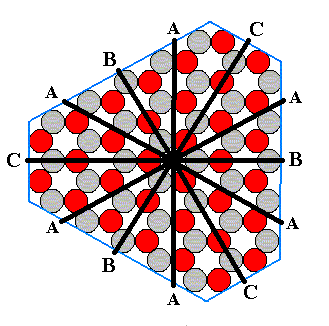
Figure 9. If the A-faces of the ionic crystal are assumed to be the fastest, as in Figure 9 of Part IV, the crystal's shape must be a combination of two triangles, as long as the B- and C-faces remain in existence. The corresponding Vector Rosette of Actual Growth is indicated. When growth is prolonged the C-faces will finally disappear because they are faster than the B-faces and the latter are tapering toward the C-faces. A triangular crystal will then result.
The next Figure gives the Vector Rosette of Actual Growth consisting of corner-pointed vectors only.
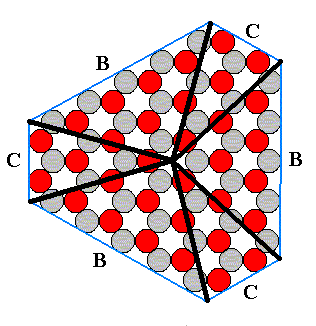
Figure 10. Sufficient and necessary Vector Rosette of Actual Growth for the 2-D ionic crystal of Figure 9 of Part IV.
The next Figure depicts the radial and interradial areas.
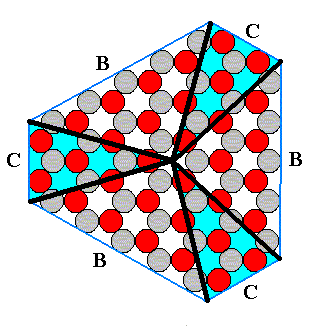
Figure 11. Radial (blue) and interradial (white) areas of the ionic crystal of the previous Figure ( The boundaries of these areas are of course more or less arbitrary).
The three antimers of the crystal are depicted in the next Figure.

Figure 12. The three antimers of the 2-D ionic crystal of Figure 9 of Part IV.
According to Figure 12 the Promorph of this crystal can be represented by an equilateral triangle (which has the same symmetry as a three-fold pyramid), and as such belongs to (a 2-D analogue of) the Anisopola triactinota of the Promorphological System. See Figure 22 of Part IV.
If, finally, the C-faces of the 2-D ionic crystal are assumed to be the slowest growing faces, then a triangular crystal will result as soon as the other faces have grown themselves out of existence :
Figure 13. If the C-faces of the 2-D ionic crystal (still with internal P3m1 symmetry) are the slowest growing faces, a triangular crystal will finally result.
The Vector Rosette of Actual Growth, as consisting of the corner-pointed vectors only, is given in the next Figure.
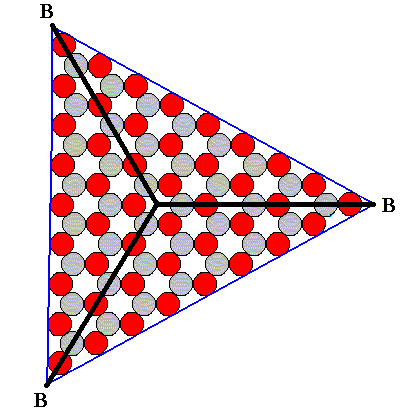
Figure 14. (Sufficient and necessary) Vector Rosette of Actual Growth of the 2-D ionic crystal of Figure 13.
The radial and interradial areas are indicated in the next Figure.
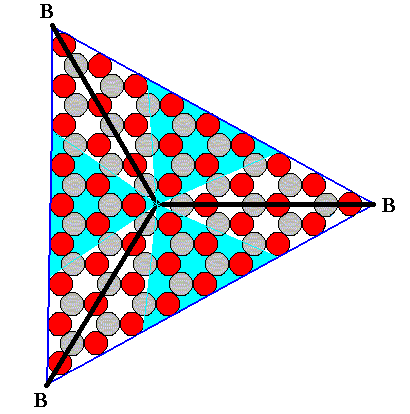
Figure 15. Radial (blue) and interradial (white) areas of the crystal of Figure 13 ( The boundaries of these areas are of course more or less arbitrary).
The next Figure indicates the three antimers of the crystal.
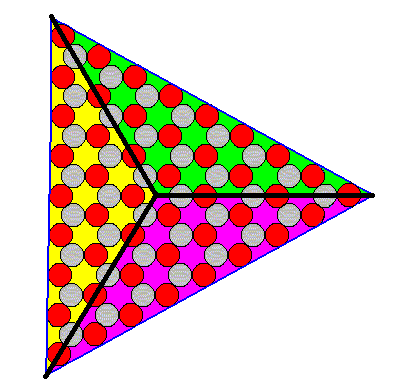
Figure 16. The three antimers of the 2-D ionic crystal of Figure 13.
According to Figure 16 the Promorph of this crystal can be represented by an equilateral triangle (having the same symmetry as a three-fold pyramid), and as such belongs to (a 2-D analogue of) the Anisopola triactinota of the Promorphological System. See Figure 22 of Part IV.
It is clear that the Vector Rosette of Actual Growth indicates the resulting Shape of the 2-D crystal. The same applies to three-dimensional crystals : The Vector Rosette of Actual Growth must consist of all the growth vectors, originating in the center of the crystal and going to the corners of the crystal.
In contradistinction to the shape of crystals, in organisms r e c e d i n g angles can occur, resulting for example in (regular or irregular) star-shaped organisms (like we see it in starfishes), and also c u r v e d boundaries, or even c i r c u l a r shapes, like in regular see-urgins. And although in the latter their Shape is circular, (as seen along the body's main axis) the Promorph is that of a regular 5-fold pyramid (Anisopola pentactinota), in virtue of the five ambulacral regions alternating with the five interambulacral regions, distributed around the body's main axis. So here the Vector Rosette of Actual Growth (as seen in the direction of the body's main axis) is a disc containing infinitely many growth vectors of equal length, radiating from the center of the disc, i.e. from the center (or lying a little above it) of the base of the animal's body. But even in cases like this we still can legitimately say that to determine the effective Vector Rosette of Actual Growth, we should give all (and only) those vectors that go to a corner : a circle can be seen as a polygon with infinitely many corners.
The upshot of all the foregoing and following is to put c r y s t a l s and o r g a n i s m s on the same footing with respect to Shape, Symmetry and Promorph.
We will deal with organisms later.
e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXXI.