

e-mail :

Sequel-7 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-7) continues the investigation of snow crystals.
Sequel to the Significance of Snow-Crystal Growth for the General Holistic Ontological Theory
Details of the crystallography of ice.
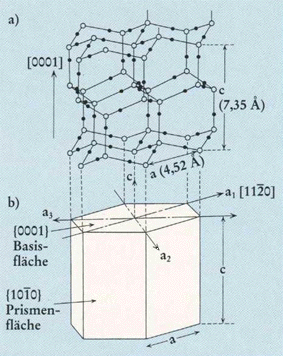
Top part of Figure : Crystallographic structure of ice I(h).
Open and solid spheres indicate the Oxygen and Hydrogen atoms, respectively. Each Oxygen atom is connected with four neighboring Oxygen atoms by Hydrogen bonds (thin solid lines), which makes a tetrapod arrangement.
Bottom part of Figure : Illustration for the corresponding crystallographic axes and planes. Basal and prism faces correspond to the {0001} and {1010} faces, respectively.
(Figure and subscript after FURUKAWA (website, Fig.4).)
REMARK : In the above Figure (top part) we should insert a hydrogen atom at the 6.30 o'clock position with respect to the center of that top part of the Figure.
Ice (H2O) can assume a large number of different crystalline structures (polymorphs), more than any other known material (LIBBRECHT (Website), BALL, P., H2O, A biography of water, 1999, 2000). At ordinary pressures the stable phase of ice is called Ice I , and the various high-pressure phases of ice number up to ice XIV so far (LIBBRECHT (website)). There are two closely related variants of Ice I : hexagonal ice I(h) [also denoted as Ih], which has hexagonal symmetry, and cubic ice I(c) [also denoted as Ic], which has a crystal structure similar to diamond. Ice 1h is the normal form of ice. Ice Ic is formed by depositing vapor at very low temperatures (below 140 K). Amorphous ice can be made by depositing water vapor onto a substrate at still lower temperatures (LIBBRECHT (website)).
The complicated changes observed in snow-crystal morphology are never related to the just mentioned crystallographic phase transitions (FURUKAWA (Website, Section 2)). Since the temperature and pressure ranges in which the snow crystals grow are extremely narrow and completely included in the region of hexagonal Ice I(h), we, when, in the ensuing discussions, referring to ice or snow, always mean Ice I(h).
According to FURUKAWA (Website) the arrangement of oxygen atoms in Ice I(h) is categorized as the Wurtzite (ZnS, zinc sulphide, see next Figure) (FURUKAWA writes "wultzite") structure according to the Space Group P63mmc. In HURLBUT, C. & KLEIN, C., Manual of Minerology, 1977 (19th ed.) p.243 the notation P63mc is used, which should be equivalent to P63/m mc, while the complete symbol for this Space Group is P 63/m 2/m 2/c (BURZLAFF, H. & ZIMMERMANN, H., Kristallographie, Grundlagen und Anwendung, Band I : Symmetrielehre, p.178).
The Point Group (which expresses the Crystal Class) derives from this Space Group, by eliminating all translations and translational elements, and, consequently reads : 6/m 2/m 2/m , group theoretically written as the product group D6 x C2 (Ibidem, p.57).
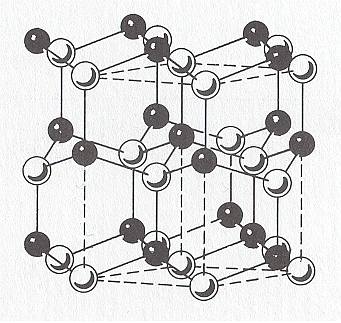
Figure above : The wurtzite type polymorph (hexagonal) of ZnS (zinc sulfide). ( The other one is the sphalerite type polymorph of ZnS, which is cubic.). Rhombic unit cell outlined ( Three such cells make up a hexagonal prism).
Sphalerite (Isometric Crystal System) is considered the low-temperature cubic polymorph of ZnS, and Wurtzite (Hexagonal Crystal System) the high-temperature polymorph stable above 10200 C at 1 atmosphere pressure. The Wurtzite polymorph (Space Group P63mc), with Zn atoms (white) in hexagonal closest packing, shows a very large number of stacking sequences, referred to as wurtzite polytypes, which differ in the length of their c-axes (as measured in one unit cell).
(After HURLBUT, C. & KLEIN, C., Manual of Mineralogy, 1977, p.243.)
In what follows I will try to unravel the lattice structure of ice, based on the Figures in the literature available to me so far. These Figures are from several authors, among them, LIBBRECHT (2003), BALL (1999) and FURUKAWA (website, 1997 or thereafter).
We begin by analysing the Figure by FURUKAWA, depicting the crystal lattice of ice, as was given above . Its upper part is again reproduced here :
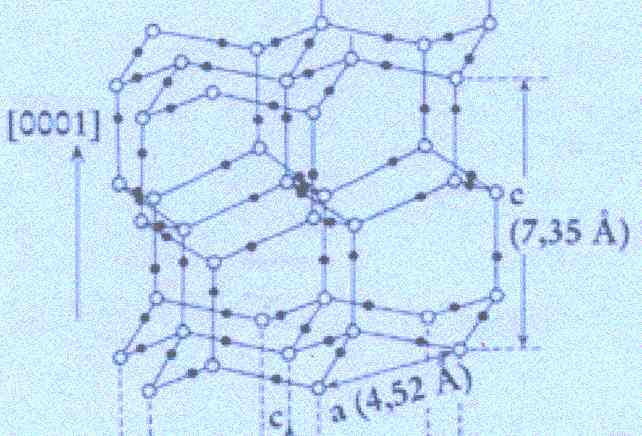
Figure above : Lattice structure of ice.
(After FURUKAWA (website))
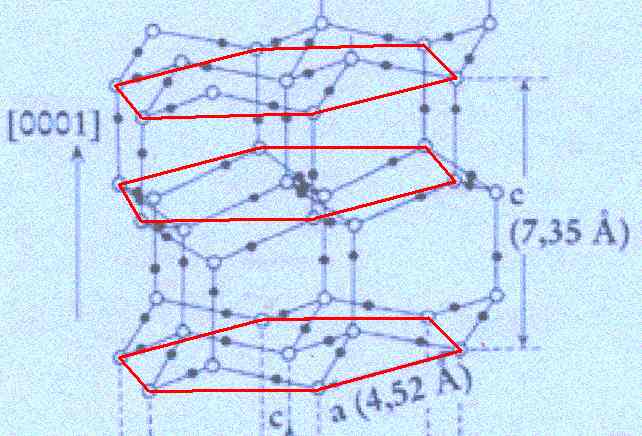
Figure above : Lattice structure of ice.
In the depicted structure we can discern three planes consisting of hexagons (one shown for each plane). Such a hexagon consists of six water molecules at its vertices and one at its center. See also next Figure.
(Adapted from FURUKAWA (website))
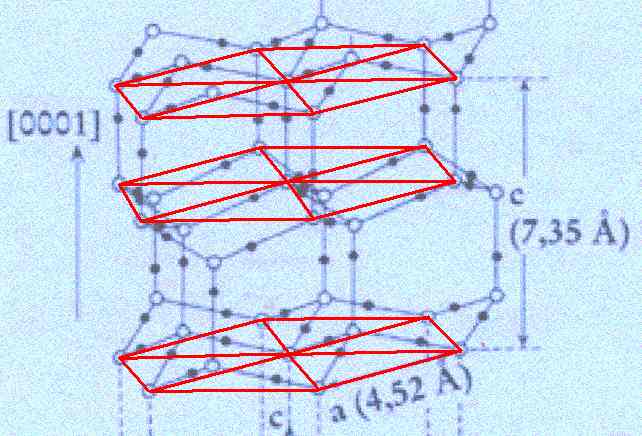
Figure above : Lattice structure of ice.
In the depicted structure we can discern three planes consisting of hexagons (one shown for each plane). Such a hexagon consists of six water molecules at its vertices and one at its center. Each hexagon can be divided in six triangular sectors.
(Adapted from FURUKAWA (website))

Figure above : Lattice structure of ice.
Each a hexagon consists of six water molecules at its vertices and one at its center. Associated with each alternate triangular sector of such a hexagon (thus with three of the six triangular sectors) is another water molecule (the oxygen atom of which is indicated by yellow coloring). See also next Figure.
(Adapted from FURUKAWA (website))
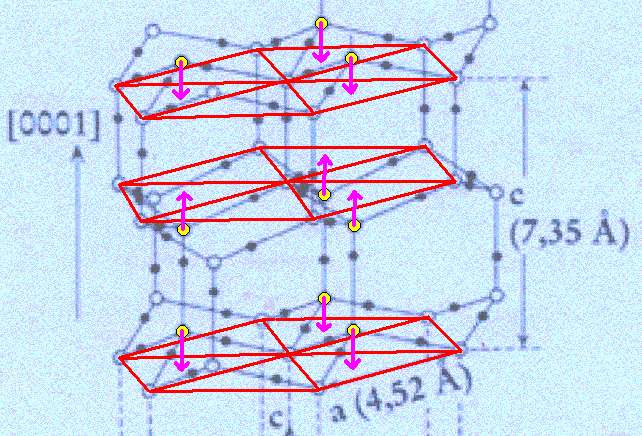
Figure above : Lattice structure of ice.
Each a hexagon consists of six water molecules at its vertices and one at its center.
The association of the water molecule, mentioned in the previous Figure's subscript, with a triangular sector of the hexagon is indicated by arrows.
(Adapted from FURUKAWA (website))
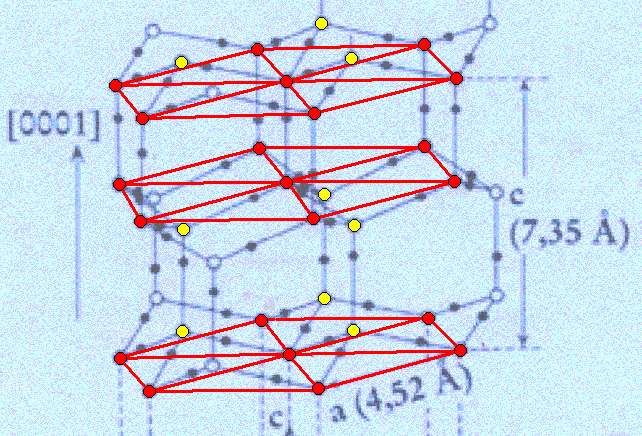
Figure above : Lattice structure of ice.
We thus have planes consisting of 6+1 water molecules arranged into centered hexagons, and in addition to these we have planes each consisting of three water molecules ( These latter planes in fact also consist of hexagons, which will become evident when we extend them horizontally. They are, however, horizontally shifted with respect to the former). The mentioned three molecules are above or under the corresponding triangular sectors of the hexagons.
We now show how this structure looks like when seen from above, i.e. seen along the crystallographic c-axis, or, equivalently, seen as projected onto the basal plane {0001} of the hexagonal prism.

Figure above : The structure, seen along the crystallographic c-axis, of the above mentioned hexagonal layers as part of the lattice structure of ice. As such this two-dimensional lattice admits of hexagonal unit meshes, but the smallest possible unit mesh is a rhombus (with 60 and 120 degree angles), as indicated. Alternative (and equivalent) rhombic unit meshes are also indicated. Red dots represent atoms or molecules.

Figure above : The structure, seen along the crystallographic c-axis, of the above mentioned two types of layers as part of the lattice structure of ice. Red or blue dots represent water molecules. Alternative triangular sectors are associated with water molecules (blue). See also next Figure.
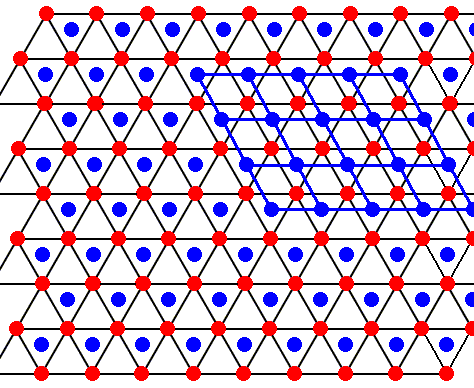
Figure above : Same as previous Figure.
The layer with the blue dots is identical to the layer with the red dots. The only difference between the two is that they are shifted with respect to each other.
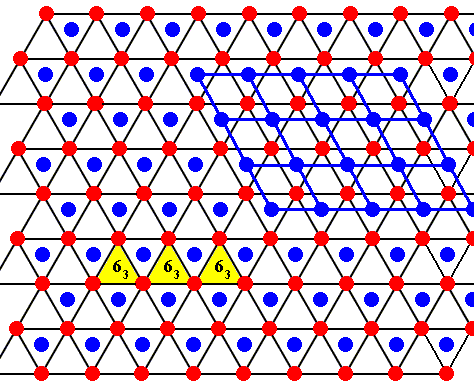
Figure above : Same as previous Figure.
If seen, not as a projection, but as a three-dimensional structure, consisting of hexagonal layers (two types) of molecules, one type shifted with respect to the other, then we can discern the following :
The center of each empty triangle is the location of a six-fold screw axis (perpendicular to the plane of the drawing), namely a 63 axis, which is a combined symmetry transformation : rotation by 600 followed by a translation along the rotation axis. The length of the translation is half the unit translation along the crystallographic c-axis. Three of such screw axes indicated.
Each molecule itself (indicated as a red or blue dot) is the location of a 3-fold rotation axis.
On the basis of the above we have indicated the position of one 63 axis in FURUKAWA's drawing of the lattice structure of ice :
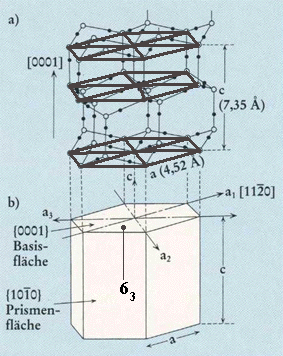
Top part of Figure : Crystallographic structure of ice I(h).
Open and solid spheres indicate the Oxygen and Hydrogen atoms, respectively. Each Oxygen atom is connected with four neighboring Oxygen atoms by hydrogen bonds (thin solid lines), which makes a tetrapod arrangement.
Bottom part of Figure : Illustration for the corresponding crystallographic axes and planes. Basal and prism faces correspond to the {0001} and {1010} faces, respectively.
Position of one 63 axis indicated. It runs parallel to the c-axis.
(Figure and subscript adapted from FURUKAWA (website, Fig.4).)
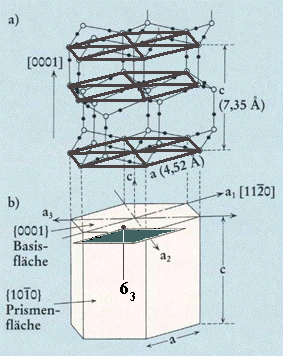
Figure above : Same as previous Figure.
Top face of alternative unit cell indicated (black). The corners of this latter unit cell are the locations of 63 screw axes. Such a unit cell can, together with three other such unit cells, form a hexagonal prism, the central axis of which is a 63 axis. When all translations are eliminated, i.e. if we derive the Point Group symmetry (indicating the Crystal Class) from the Space Group symmetry, this axis will become a six-fold rotation axis.
We continue with our above series of ice lattice drawings, depicting hexagonal layers stacked along the c-axis, layers that are (horizontally) shifted with respect to each other. The view direction is down along the c-axis.
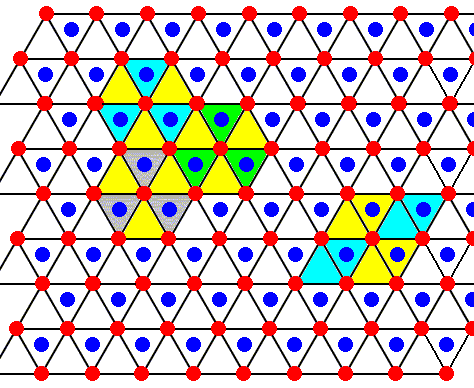
Figure above : The structure, seen along the crystallographic c-axis, of the above mentioned two types of layers as part of the lattice structure of ice. Red or blue dots represent water molecules. Alternative triangular sectors are associated with water molecules (blue). Possible hexagonal unit meshes (six triangles), and rhombic unit meshes (two triangles), are indicated.

Figure above : Same as previous Figure.
Each water molecule in an ice lattice is connected to four others by hydrogen bonds. For each water molecule three such bonds are shown (the fourth bond is perpendicular to the plane of the drawing and connects the depicted structure with a copy of it). See next Figure where the construction of the pattern of hydrogen bonds is completed.

Figure above : Same as previous Figure.
Each water molecule in an ice lattice is connected to four others by hydrogen bonds. For each water molecule three such bonds are shown (the fourth bond is perpendicular to the plane of the drawing and connects the depicted structure with a copy of it). In the present Figure the construction of the pattern of hydrogen bonds is completed. It turns out to be a hexagonal array, consisting of open hexagons (Hydrogen bonds perpendicular to the plane of the drawing not shown). See also next Figure.
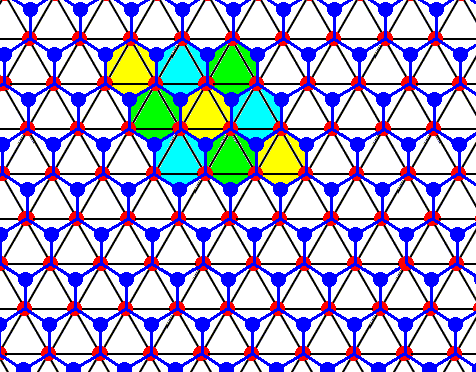
Figure above : Same as previous Figure.
Open hexagons, each consisting of six water molecules, indicated. As such they represent the structure of ice.
If we now remove all black connection lines we're left with an array of open hexagons :
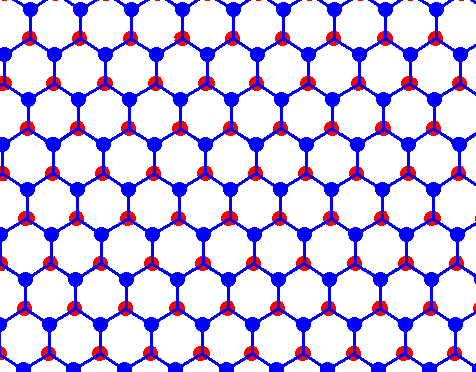
Figure above : Structure of ice, seen along the crystallographic c-axis.
Each dot (red or blue) represents a water molecule. Each such water molecule connects with four others by hydrogen bonds. Three such bonds shown for each water molecule. The fourth bond is perpendicular to the plane of the drawing.
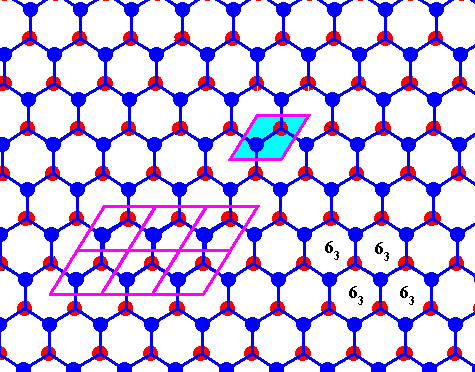
Figure above : Same as previous Figure.
Possible rhombic unit cell indicated. The the center of each hexagon is the location of a 63 screw axis (four of them indicated), if the Figure is interpreted as representing a 3-dimensional view (down the c-axis).
If the Figure is 2-dimensionally interpreted, then we see a rhombic unit mesh, containing two 3-fold rotation axes (coinciding with the two molecules of that mesh), and a 6-fold rotation axis at each of its corners.
The last obtained picture of the lattice structure of ice, can now be compared with some other Figures from the literature, that (also) depict the ice lattice as seen along the c-axis :
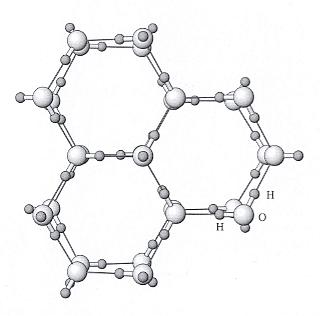
Figure above : Ice structure viewed down the c axis (i.e. down the 6-fold rotation axis of a single crystal). Water molecules consisting of one oxygen (large sphere) and two hydrogens (small spheres) are arranged in a hexagonal array. Hydrogen bonds between water molecules are shown with thinner lines. The positions of the H (hydrogen) and O (oxygen) are shown accurately, but the sizes of the atoms are not.
(After NESSE, W., Introduction to Mineralogy, 2000.)
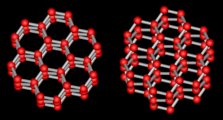
Figure above : Ice structure.
Left image : Viewed a little obliquely down the c axis.
Right image : Viewed still more obliquely.
The water molecules in ice form a hexagonal lattice. Each red ball represents an oxygen atom, and the grey sticks represent hydrogen atoms. There are two hydrogens for each oxygen, making the usual H2O.
(After LIBBRECHT (website))
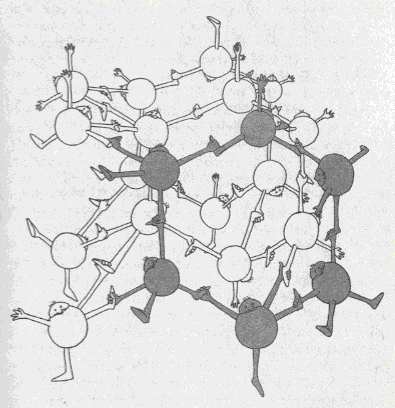
Figure above : Structure of ice.
Each water molecule is hydrogen-bonded to four others in an arrangement that displays hexagonal symmetry. One of the hexagonal rings is highlighted in grey.
(After BALL, P., "H2O, a biography of water", 1999, 2000.)
In what follows, we compare two Figures from the literature that are supposed to depict the lattice structure of ice. One of these Figures was already given above in the present document, while the other was already given in Part XXIX Sequel-3.
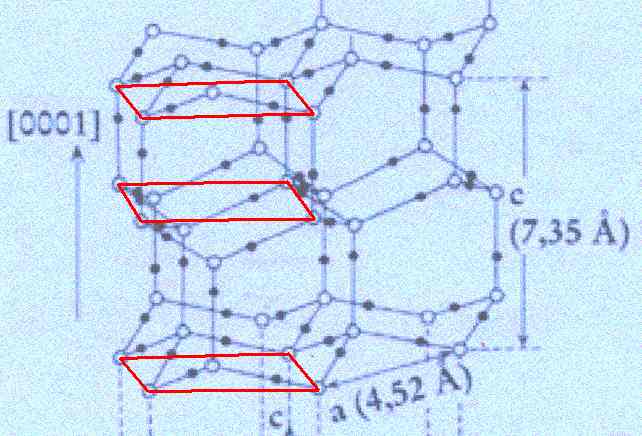
Outlining one unit cell . . .
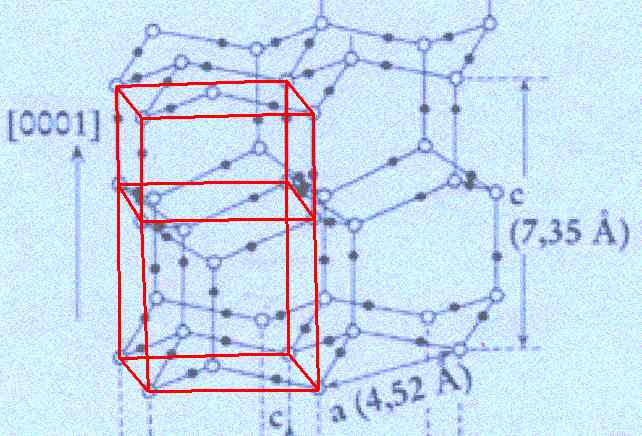
Figure above : In the structure of the ice lattice (as depicted by FURUKAWA) one unit cell is outlined. Its top and bottom faces have the shape of a rhombus with angles of 60 and 120 degrees.
Now we can compare the two representations (resp. from FURUKAWA and NESSE) of the lattice structure of ice :
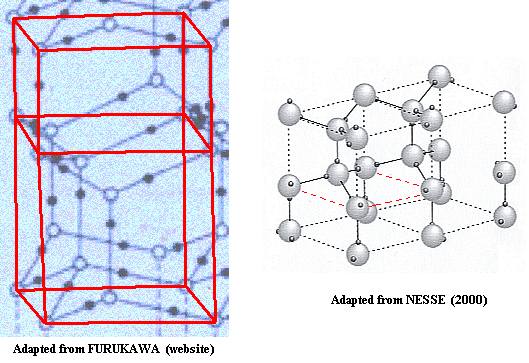
Figure above : Lattice structure of Ice. Comparison of the two above mentioned representations.
For the right image to be conveniently comparable with the left one, it should be three-dimensionally rotated about a horizontal axis parallel to the plane of the drawing.
In the next two Figures we indicate the precise correspondences by using the letters
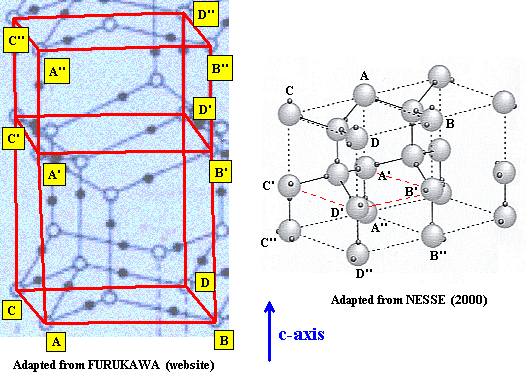
Figure above : Lattice structure of Ice. Comparison of the two above mentioned representations.
The three levels of the unit cell are compared : A, B, C, D and A', B', C', D' and A'', B'', C'', D''.
Now we indicate the other water molecules (E and E') belonging to the above depicted unit cell :
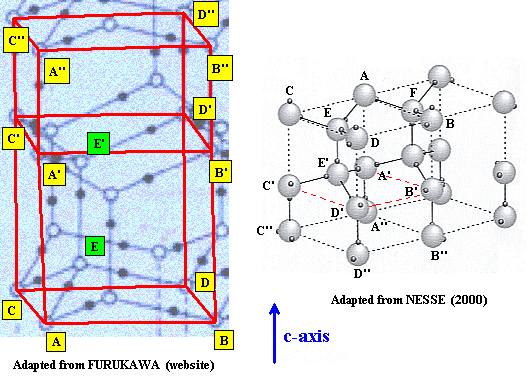
Figure above : All water molecules of the unit cell are now accounted for.
And if we look at this structure down along the c-axis, then we can detect the open hexagonal structure referred to above and also (referred to) still higher up .
In the right image (and, by consequence also in the left image) of the present Figure we can see (part of) this structure : D - E - A - F - B . These molecules form, together with one other molecule, which is not depicted here, an open hexagon. And indeed the molecules of this hexagon are sequentially connected to each other by chemical bonds (represented by the six sides of the hexagon), as can be seen in the Figure (if we complete it by adding a (third) unit cell). See also next Figure.
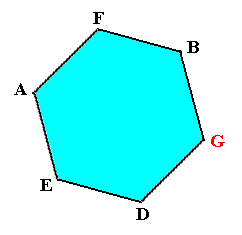
Figure above : When the above depicted lattice structure (of Ice) is seen down along the crystallographic c-axis, we see open hexagons, the corners of which are occupied by water molecules. Such an open hexagon is not flat but has a zig-zag surface, because the atoms E, F, and G reside in a slightly different (but parallel) plane with respect to that in which the atoms D, A and B reside. See the Figures given above, i.e. respectively here, here and here.
This open hexagon D - E - A - F - B - G can also be identifiied in the drawings we've made earlier :
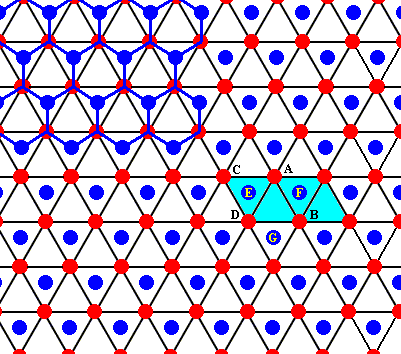
Figure above : Two rhombic unit cells (blue) -- of the drawing given earlier -- are indicated. They correspond exactly with the two unit cells as given in the right image of the Figure (of NESSE) given earlier.

Figure above : Same as previous Figure. One can see that also here an open hexagon is formed by the water molecules D - E - A - F - B - G (as was the case in NESSE's Figure).
We can now conclude that the Wurtzite structure referred to above has a structure different from that of ice : The Wurtzite structure represents Hexagonal Closest Packing of its Zinc atoms, while the Ice structure does not, although its structure is very similar. And it seems that this similarity entails that their Space Group symmetry is identical, namely P 63/m 2/m 2/c.
So far so good for the lattice structure of ice.
In the next document we continue our investigation of snow crystals, as to their (macroscopic) morphology.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-8.