

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Regular Hexagon (Promorphs)
The Vector Rosette of Actual Growth of a regularly-hexagonal crystal, i.e. of any two-dimensional crystal having as its intrinsic shape (when fully developed) the Regular Hexagon (which itself has D6 symmetry) and possessing whatever (possible) intrinsic (point) symmetry, is as follows (blue lines) :
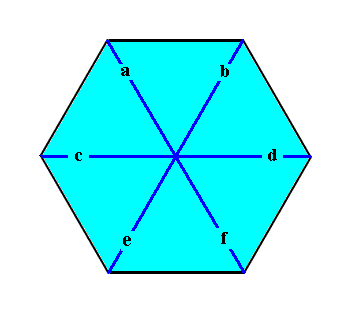
This Vector Rosette, viz. a vector rosette of a regularly-hexagonal two-dimensional crystal, in fact consists of six vectors, a, b, c, d, e, f, each originating in the center of the crystal and ending up at a corner. As such it encodes the crystal's shape.
REMARK :
As in the previous document, we will use the term "hexagonal" , where this term should be taken to mean "regularly-hexagonal", unless indicated otherwise.
As we saw in the previous document, an intrinsically hexagonal crystal shape (with respect to two-dimensional crystals) is supported by all plane groups except the groups P4, P4mm, and P4gm. So the supporting plane groups are :
P6mm, P6, P31m, P3m1, P3, P2mm, P2mg, P2gg, C2mm, Pm, Pg, Cm, P2 and P1.
See also the table in the previous document where, in addition to the supporting plane groups, the corresponding point groups are indicated, and the number of crystallographic Forms needed to construct a hexagonal crystal in each case (of point symmetry).
We will now consider several possible cases of the given example of a hexagonal two-dimensional crystal as depicted just above, with respect to possible promorphs.
D6 symmetry.
The next Figure indicates the symmetry elements of an intrinsic D6 crystal.
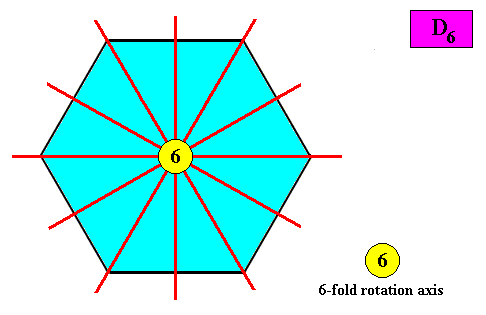
Figure above : Symmetry elements (with respect to point symmetry) of a two-dimensional crystal with intrinsic D6 symmetry : six mirror lines, and a 6-fold rotation axis at their point of intersection.
Only one crystallographic Form is needed to conceptually construct a hexagonal crystal with intrinsic D6 symmetry :
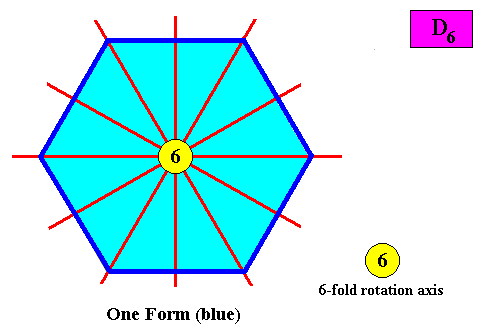
Figure above : Only one crystallographic Form is needed to conceptually construct a hexagon-shaped intrinsic D6 two-dimensional crystal : An initially given crystal face perpendicular to one of the mirror lines implies five others in virtue of the 6-fold rotation axis, resulting in one closed Form (dark blue) having the shape of a regular hexagon.
D6 symmetry and six antimers.
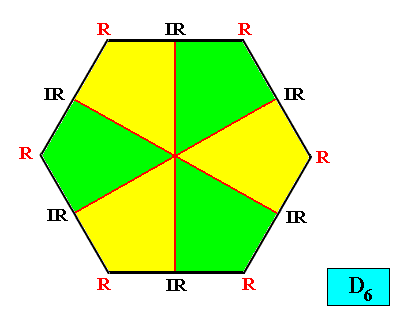
Figure above : The six antimers (yellow, green) of an intrinsically hexagon-shaped two-dimensional crystal with intrinsic D6 symmetry. Radial (R) and interradial (IR) directions indicated.
And with the Vector Rosette of Actual Growth added :
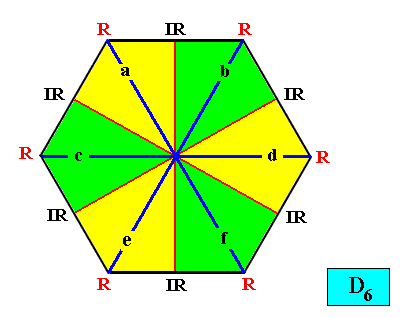
Figure above : Two-dimensional hexagonal D6 crystal with Vector Rosette of Actual Growth added. The six vectors, a, b, c, d, e, f, coincide with the median lines of the antimers, and thus fully express the promorph.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D6 symmetry. It is a regular hexagon, and as such the two-dimensional analogue of the regular six-fold pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Homostaura Isopola hexactinota .
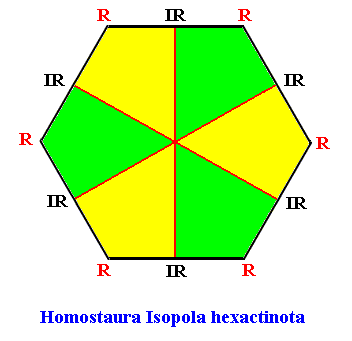
Figure above : Promorph of the above discussed two-dimensional hexagonal D6 crystal. The six antimers are indicated (green, yellow).
The next two Figures depict the corresponding three-dimensional analogue of our just established promorph.
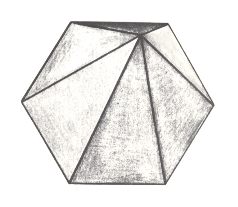
Figure above : Slightly oblique top view of a 6-fold regular pyramid as a representative of the Homostaura Isopola hexactinota .
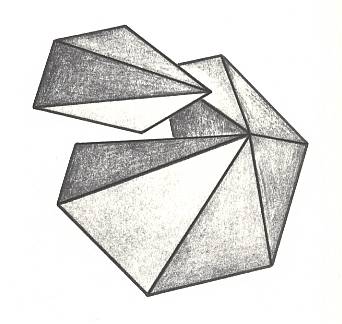
Figure above : Slightly oblique top view of a 6-fold regular pyramid as a representative of the Homostaura Isopola hexactinota . One antimer is taken out.
C6 symmetry.
The next Figure indicates the symmetry elements of an intrinsic C6 crystal.
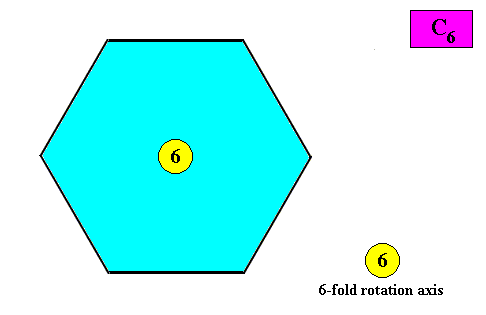
Figure above : Symmetry elements (with respect to point symmetry) of a two-dimensional crystal with intrinsic C6 symmetry : a 6-fold rotation axis at the center of the crystal.
Also in the present case only one crystallographic Form is needed to conceptually construct a hexagonal crystal with intrinsic C6 symmetry :
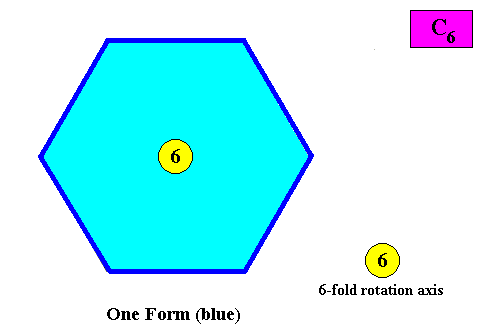
Figure above : Only one crystallographic Form is needed to conceptually construct a hexagon-shaped intrinsic C6 two-dimensional crystal : An initially given crystal face implies five others in virtue of the 6-fold rotation axis, resulting in one closed Form (dark blue) having the shape of a regular hexagon.
C6 symmetry and six antimers.
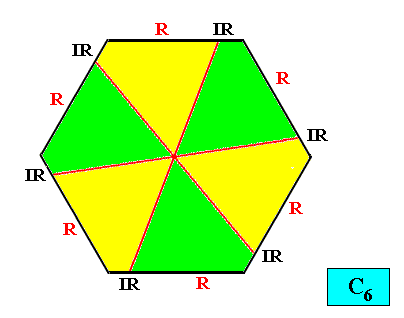
Figure above : The six (asymmetric) antimers (yellow, green) of an intrinsically hexagon-shaped two-dimensional crystal with intrinsic C6 symmetry. Radial (R) and interradial (IR) directions indicated.
And with the Vector Rosette of Actual Growth added :
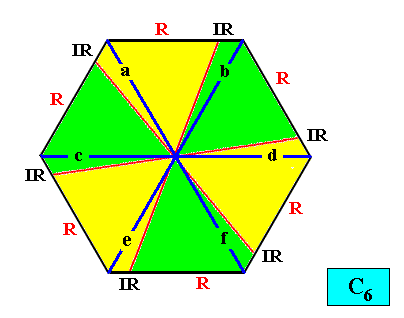
Figure above : Two-dimensional hexagonal C6 crystal with Vector Rosette of Actual Growth added. The six vectors, a, b, c, d, e, f, coincide with the antimers (i.e. each one corresponds to an antimer), and thus partially express the promorph (partially, because they do not express the asymmetry of the antimers).
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic C6 symmetry. It is a regular gyroid hexagon, and as such the two-dimensional analogue of the regular gyroid six-fold pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Homogyrostaura hexamera .
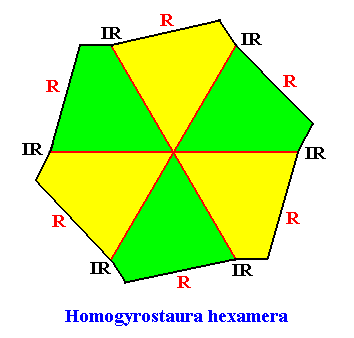
Figure above : Promorph of the above discussed two-dimensional hexagonal C6 crystal. The six antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established promorph.
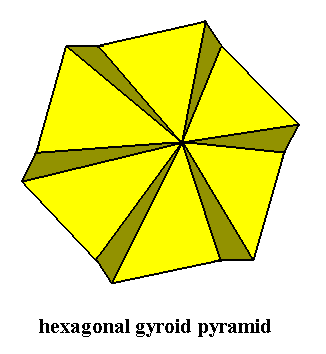
Figure above : Three-dimensional analogue of the promorph of the above discussed two-dimensional hexagonal C6 crystal : A regular gyroid pyramid (slightly oblique top view) with six antimers ( Homogyrostaura hexamera ).
D3 symmetry.
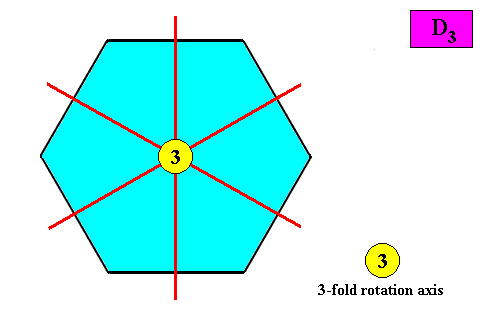
Figure above : Possible configuration of symmetry elements of a two-dimensional hexagon-shaped D3 crystal : Three mirror lines (red) connecting opposite centers of sides of the hexagon, and a three-fold rotation axis at their point of intersection.
Within this configuration of symmetry elements two crystallographic Forms are needed to conceptually construct a hexagon-shaped D3 crystal :
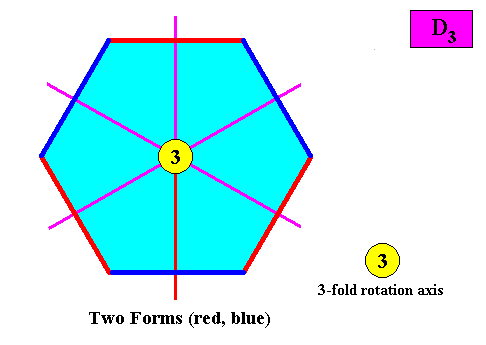
Figure above : Given the above configuration of symmetry elements, two Forms are needed to conceptually construct a hexagonal D3 two-dimensional crystal : An initially given crystal face (red) implies two others in virtue of the mirror lines ( The action of the 3-fold rotation axis does not create more faces in addition to the ones already obtained so far). The resulting three faces constitute one open Form. A second initially given crystal face (blue) also implies two more faces, resulting in a second open Form (three faces). The two Forms together constitute the whole hexagon-shaped crystal.
Apart from the above depicted configuration of symmetry elements of a two-dimensional hexagon-shaped intrinsic D3 crystal, there is another such configuration possible, viz. three mirror lines connecting opposite corners of the hexagon. See next Figure.
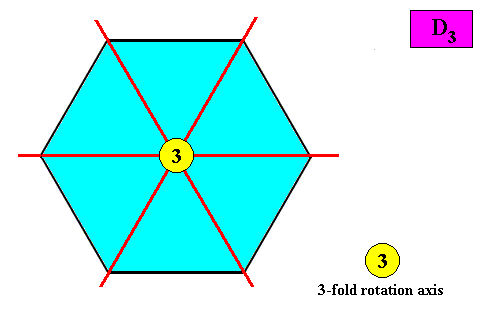
Figure above : Alternative configuration of symmetry elements of a two-dimensional hexagon-shaped D3 crystal : Three mirror lines (red) connecting opposite corners of the hexagon, and a three-fold rotation axis at their point of intersection.
Within this configuration of symmetry elements only one crystallographic Form is needed to conceptually construct a hexagon-shaped intrinsic D3 two-dimensional crystal :
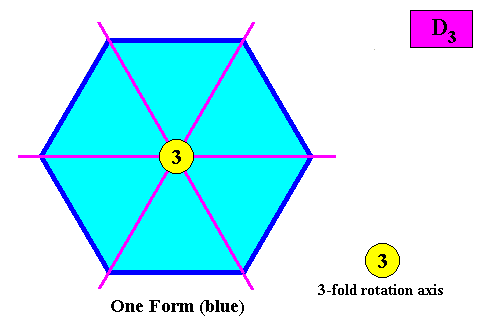
Figure above : Given the above alternative configuration of symmetry elements (mirror lines connecting opposite corners), only one Form is needed to conceptually construct a hexagonal D3 two-dimensional crystal : An initially given crystal face (blue) implies, to begin with, one other face in virtue of the nearest mirror line. But these two faces directly imply four others in virtue of the 3-fold rotation axis, resulting in one closed Form, consisting of six faces, together constituting the whole hexagonal crystal. And because with this configuration of symmetry elements (mirror lines connecting opposite corners of hexagon) the minimum number of crystallographic Forms (viz. one) is needed to conceptually construct our two-dimensional hexagon-shaped D3 crystal, we will use this configuration in our discussions regarding promorphs.
D3 symmetry and three antimers.
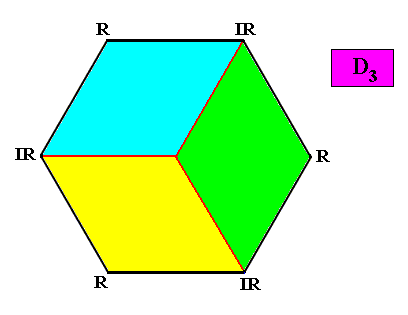
Figure above : The three antimers (yellow, green, blue) of an intrinsically hexagon-shaped two-dimensional crystal with intrinsic D3 symmetry. Radial (R) and interradial (IR) directions indicated.
And with the Vector Rosette of Actual Growth added :
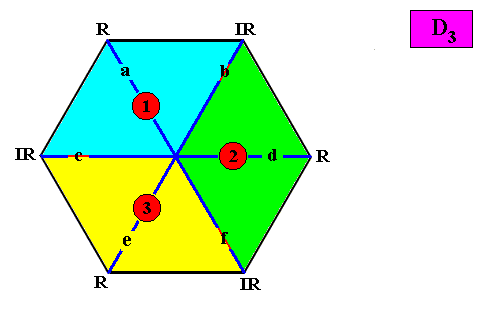
Figure above : Two-dimensional hexagonal D3 crystal with Vector Rosette of Actual Growth added. The six vectors, a, b, c, d, e, f, alternately coincide with the median lines of the antimers and the lines separating adjacent antimers. The three antimers (green, yellow, blue) are indicated by numerals.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D3 symmetry. It is an equilateral triangle (regular trigon), and as such the two-dimensional analogue of the regular three-fold pyramid.
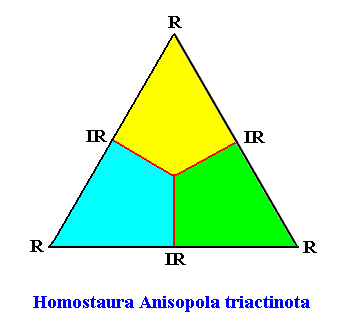
Figure above : Promorph of the above discussed two-dimensional hexagon-shaped D3 crystal. The three antimers are indicated (green, yellow, blue).
The next Figure gives the three-dimensional analogue of our just established (two-dimensional) promorph.
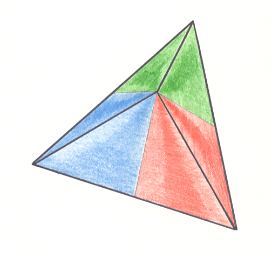
Figure above : Slightly oblique top view of a regular pyramid with three antimers (indicated by colors) as the stereometric basic form representing the Homostaura Anisopola triactinota .
C3 symmetry.
The next Figure indicates the symmetry elements of an intrinsic C3 crystal.
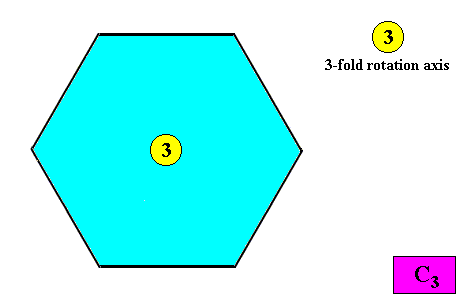
Figure above : Symmetry elements (with respect to point symmetry) of a two-dimensional crystal with intrinsic C3 symmetry : only a 3-fold rotation axis at the center of the crystal.
Two crystallographic Forms are needed to conceptually construct a hexagonal crystal with intrinsic C3 symmetry :
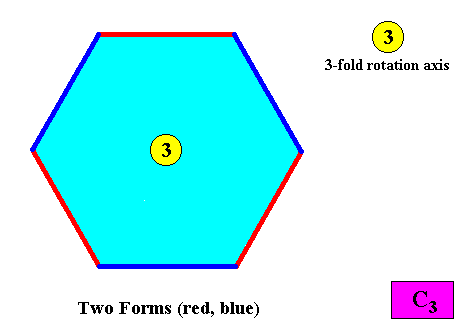
Figure above : Two crystallographic Forms are needed to conceptually construct a hexagon-shaped intrinsic C3 two-dimensional crystal : An initially given crystal face (red) implies two others in virtue of the 3-fold rotation axis, resulting in one open Form consisting of three faces. A second initially given crystal face (blue) also implies two other faces, also in virtue of the 3-fold rotation axis, resulting in a second open Form, also consisting of three faces. The two Forms together constitute the whole hexagon-shaped crystal.
C3 symmetry and three antimers.
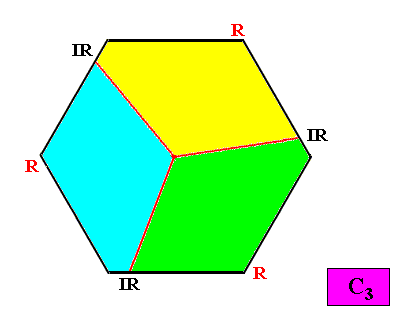
Figure above : The three (asymmetric) antimers (yellow, green, blue) of an intrinsically hexagon-shaped two-dimensional crystal with intrinsic C3 symmetry. Radial (R) and interradial (IR) directions indicated.
And with the Vector Rosette of Actual Growth added :
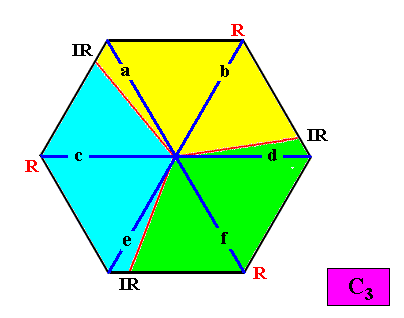
Figure above : Two-dimensional hexagonal C3 crystal with Vector Rosette of Actual Growth added. Each of the three vector pairs, (a, b), (d, f), and (e, c), of the six vectors, a, b, c, d, e, f, coincides with an antimer (i.e. lies within an antimer).
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic C3 symmetry. It is a regular gyroid trigon (regular gyroid triangle), and as such the two-dimensional analogue of the regular gyroid three-fold pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Homogyrostaura trimera .
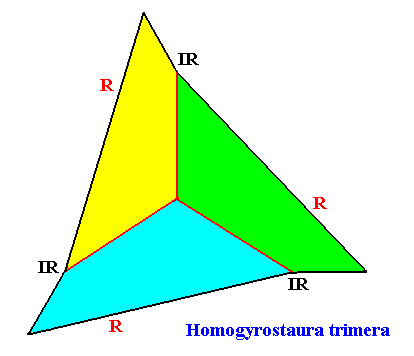
Figure above : Promorph of the above discussed two-dimensional hexagonal C3 crystal. The three antimers are indicated (green, yellow, blue).
The next Figure depicts the three-dimensional analogue of our just established promorph.
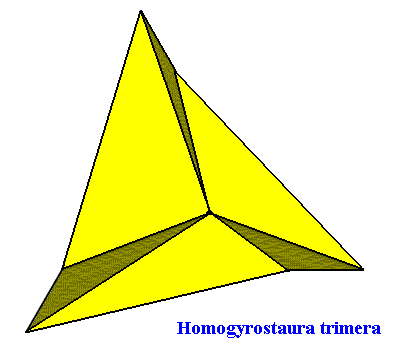
Figure above : Three-dimensional analogue of the promorph of the above discussed two-dimensional hexagonal C3 crystal : A regular gyroid pyramid (slightly oblique top view) with three antimers ( Homogyrostaura trimera ).
D2 symmetry.
The next Figure indicates the symmetry elements of an intrinsic D2 crystal.
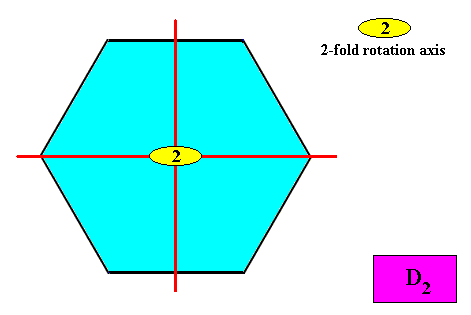
Figure above : Symmetry elements (with respect to point symmetry) of a two-dimensional crystal with intrinsic D2 symmetry : Two mirror lines perpendicular to each other, and a 2-fold rotation axis at their point of intersection.
Two crystallographic Forms are needed to conceptually construct a hexagonal crystal with intrinsic D2 symmetry :
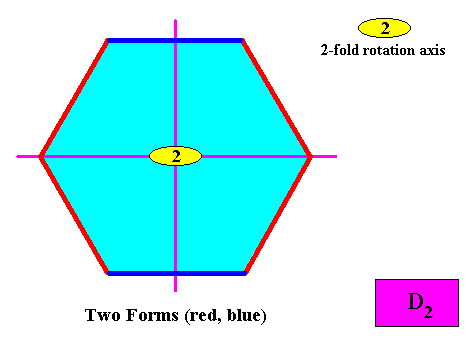
Figure above : Two crystallographic Forms are needed to conceptually construct a hexagon-shaped intrinsic D2 two-dimensional crystal : An initially given crystal face (red) implies, to begin with, one other face in virtue of the nearest mirror line, and then the two faces are reflected by the other mirror line, all this resulting in an open Form consisting of four faces. A second initially given crystal face (blue) implies one other face, in virtue of the 2-fold rotation axis, resulting in a second open Form, consisting of two faces. The two Forms together constitute the whole hexagon-shaped crystal.
Any even number of antimers can occur in two-dimensional crystals with intrinsic D2 symmetry.
D2 symmetry and four antimers.
Interradial configuration.
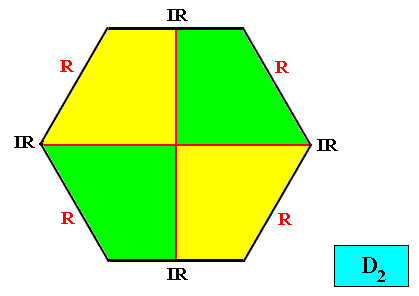
Figure above : Two-dimensional hexagon-shaped D2 crystal with four antimers (green, yellow) in interradial configuration.
And with the Vector Rosette of Actual Growth added :
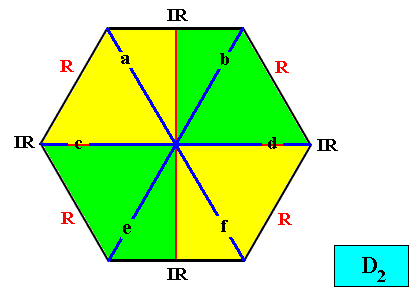
Figure above : Two-dimensional hexagon-shaped D2 crystal with four antimers (green, yellow) in interradial configuration. Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D2 symmetry, and with four antimers in interradial configuration. It is a rectangle, and as such the two-dimensional analogue of the rectangular pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Autopola Orthostaura Tetraphragma interradialia .
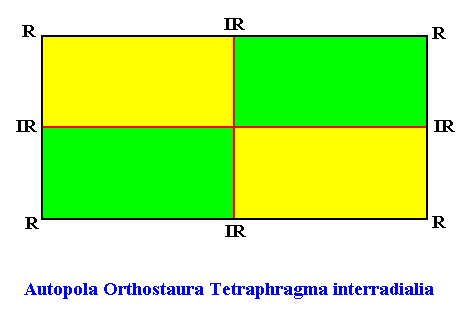
Figure above : Promorph of the above discussed two-dimensional hexagonal D2 crystal. The four antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established promorph.
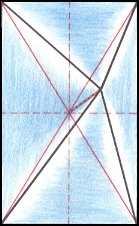
Figure above : Three-dimensional analogue of the promorph of the above discussed two-dimensional hexagonal D2 crystal : A rectangular pyramid (slightly oblique top view) with four antimers ( Autopola Orthostaura Tetraphragma interradialia ).
Radial configuration.
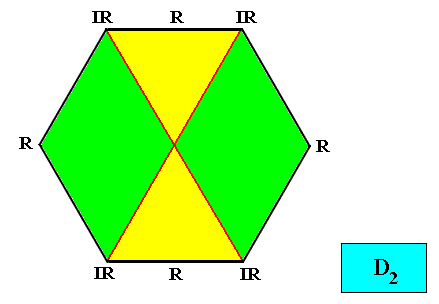
Figure above : Two-dimensional hexagon-shaped D2 crystal with four antimers (green, yellow) in radial configuration.
And with the Vector Rosette of Actual Growth added :
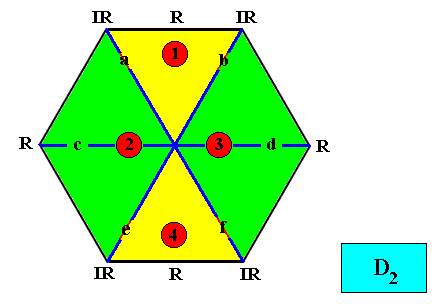
Figure above : Two-dimensional hexagon-shaped D2 crystal with four antimers (green, yellow, and indicated by numerals) in radial configuration. Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D2 symmetry, and with four antimers in radial configuration. It is a rhombus, and as such the two-dimensional analogue of the rhombic pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Autopola Orthostaura Tetraphragma radialia .
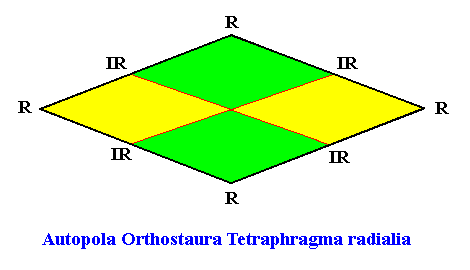
Figure above : Promorph of the above discussed two-dimensional hexagonal D2 crystal. The four antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established promorph.
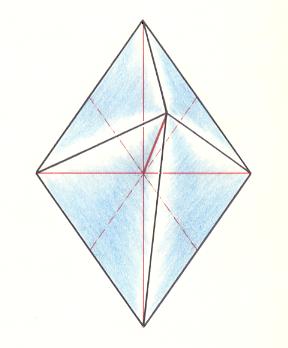
Figure above : Three-dimensional analogue of the promorph of the above discussed two-dimensional hexagonal D2 crystal : A rhombic pyramid (slightly oblique top view) with four antimers ( Autopola Orthostaura Tetraphragma radialia ).
D2 symmetry with two antimers.
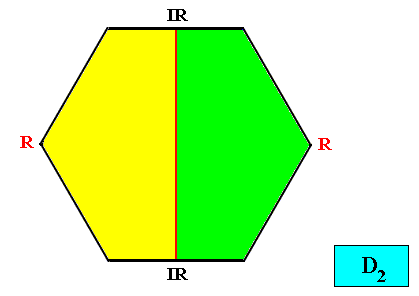
Figure above : Two-dimensional hexagon-shaped D2 crystal with two antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
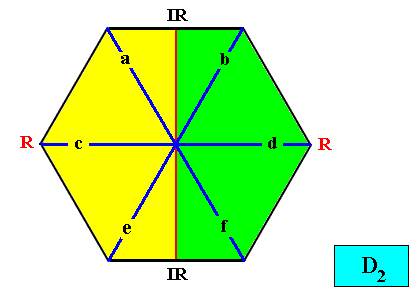
Figure above : Two-dimensional hexagon-shaped D2 crystal with two antimers (green, yellow). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D2 symmetry and with two antimers. It is a rhombus, and as such the two-dimensional analogue of the rhombic pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Autopola Orthostaura diphragma .
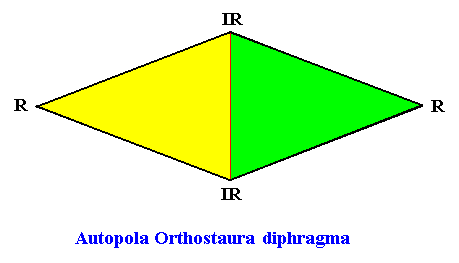
Figure above : Promorph of the above discussed two-dimensional hexagonal D2 crystal. The two antimers are indicated (green, yellow).
D2 symmetry and six antimers.
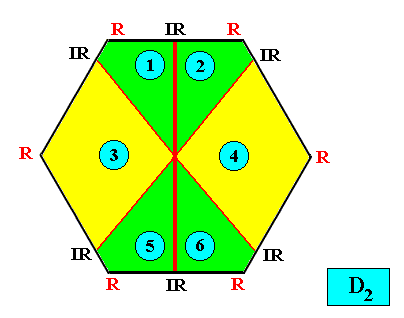
Figure above : Two-dimensional hexagon-shaped D2 crystal with six antimers (green, yellow, and indicated by numerals).
The next Figure uses another color configuration to express the same crystal.
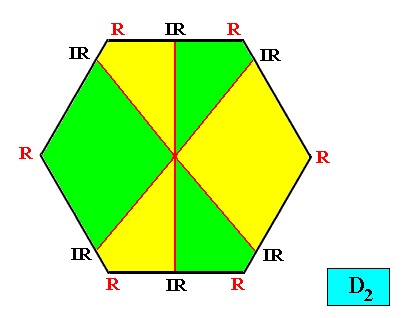
Figure above : Two-dimensional hexagon-shaped D2 crystal with six antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
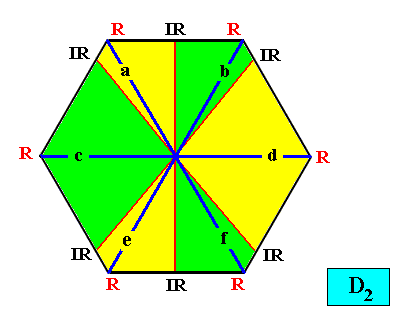
Figure above : Two-dimensional hexagon-shaped D2 crystal with six antimers (green, yellow). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D2 symmetry and with six antimers. It is a 6-fold amphitect polygon, and as such the two-dimensional analogue of the six-fold amphitect pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Autopola Oxystaura hexaphragma .
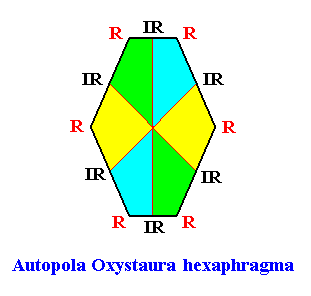
Figure above : Promorph of the above discussed two-dimensional hexagonal D2 crystal. The six antimers are indicated (green, yellow, blue).
The next Figure depicts the three-dimensional analogue of our just established (two-dimensional) promorph.
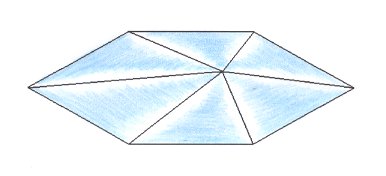
Figure above : Slightly oblique top view of a six-fold amphitect pyramid as the basic form of the Autopola Oxystaura hexaphragma . As one can see, this pyramid is flattened parallel to two of its sides, while in the previous Figure the six-fold polygon is flattened perpendicular to two of its sides, but this difference is immaterial.
D1 symmetry.
The next Figure indicates the symmetry elements of an intrinsic D1 crystal.
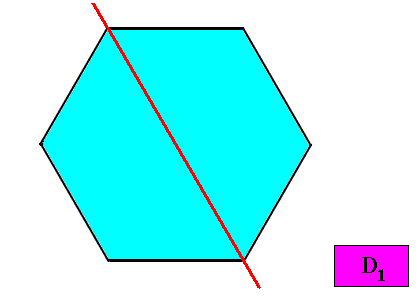
Figure above : Symmetry elements (with respect to point symmetry) of a two-dimensional crystal with intrinsic D1 symmetry : Only one mirror line.
Three crystallographic Forms are needed to conceptually construct a hexagonal crystal with intrinsic D1 symmetry :
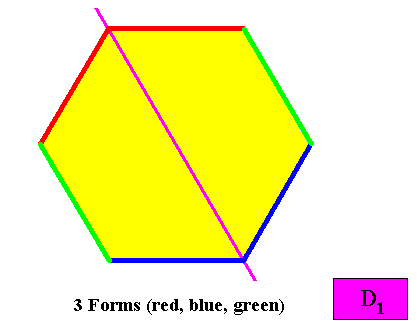
Figure above : Three crystallographic Forms are needed to conceptually construct a hexagon-shaped intrinsic D1 two-dimensional crystal : An initially given crystal face (red) implies one other face in virtue of the mirror line, resulting in an open Form consisting of two faces. A second initially given crystal face (blue) also implies one other face, in virtue of that same mirror line, resulting in a second open Form also consisting of two faces. Finally, a third initially given face (green) also implies one other face and also results in an open Form consisting of two faces. The three Forms together constitute the whole hexagon-shaped crystal.
Any number (> 1) of antimers can occur in two-dimensional crystals with intrinsic D1 symmetry.
D1 symmetry and two antimers.
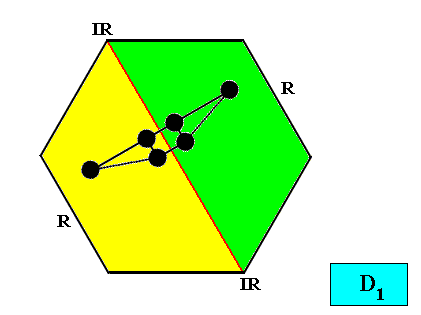
Figure above : Two-dimensional hexagon-shaped D1 crystal with two antimers (green, yellow). A motif (black) is inserted in order to express the D1 symmetry of the crystal.
And with the Vector Rosette of Actual Growth added :
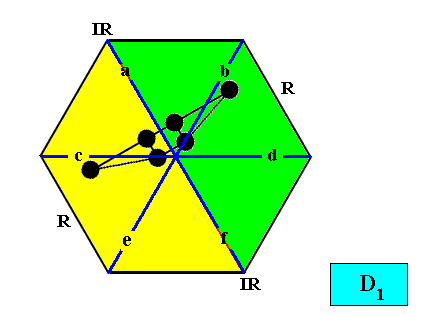
Figure above : Two-dimensional hexagon-shaped D1 crystal with two antimers (green, yellow). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
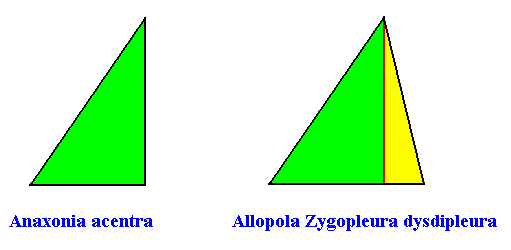
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D1 symmetry and with two antimers. It is half a rhombus (i.e. an isosceles triangle), and as such the two-dimensional analogue of half a rhombic pyramid (i.e. of an isosceles pyramid). As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Allopola Zygopleura eudipleura .
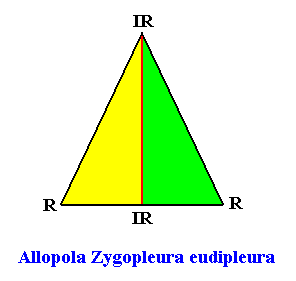
Figure above : Promorph of the above discussed two-dimensional hexagonal D1 crystal. The two antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established (two-dimensional) promorph.
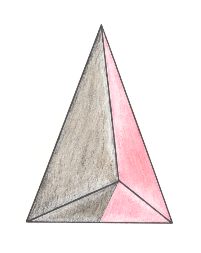
Figure above : Oblique top view of a single isosceles pyramid (i.e. of half a rhombic pyramid) as the basic form of the Allopola Zygopleura eudipleura . The two antimers are indicated by colors.
D1 symmetry with four antimers.
Interradial configuration.
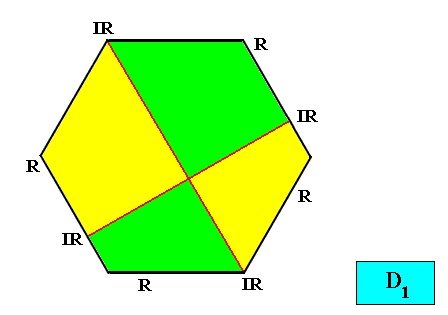
Figure above : Two-dimensional hexagon-shaped D1 crystal with four antimers (green, yellow) in interradial configuration.
The next Figure uses a different color configuration for the same crystal.
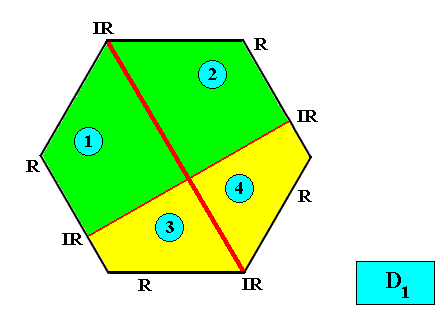
Figure above : Two-dimensional hexagon-shaped D1 crystal with four antimers (green, yellow, and indicated by numerals) in interradial configuration.
And with the Vector Rosette of Actual Growth added :
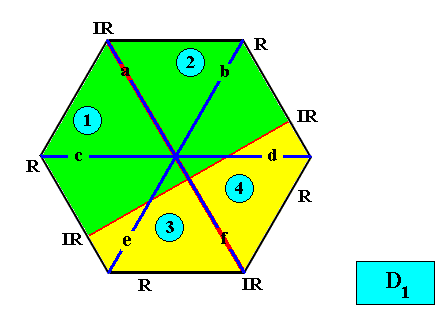
Figure above : Two-dimensional hexagon-shaped D1 crystal with four antimers (green, yellow, and indicated by numerals) in interradial configuration. Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D1 symmetry, and with four antimers in interradial configuration. It is an isosceles trapezium, and as such the two-dimensional analogue of the trapezoid pyramid (i.e. it is its base). As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Allopola Zygopleura Eutetrapleura interradialia .
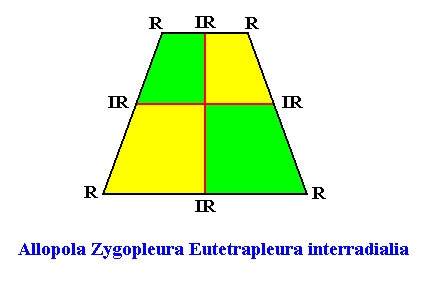
Figure above : Promorph of the above discussed two-dimensional hexagonal D1 crystal. The four antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established promorph.
Figure above : Three-dimensional analogue of the promorph of the above discussed two-dimensional hexagonal D1 crystal : Oblique top view of a trapezoid pyramid ( = antiparallelogram pyramid) with four antimers, indicated by colors ( Allopola Zygopleura Eutetrapleura interradialia ).
Radial configuration.
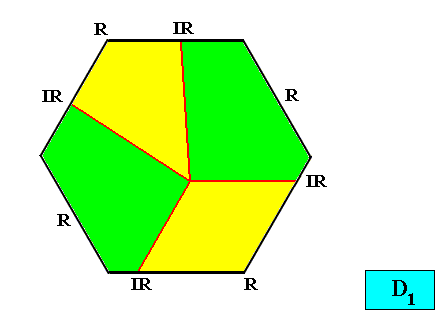
Figure above : Two-dimensional hexagon-shaped D1 crystal with four antimers (green, yellow) in radial configuration.
And with the Vector Rosette of Actual Growth added :
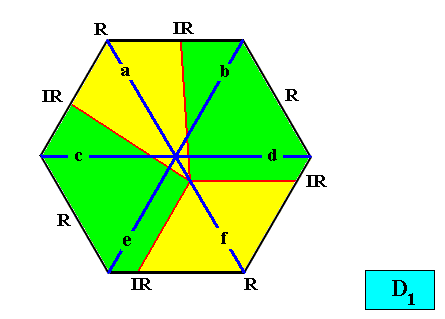
Figure above : Two-dimensional hexagon-shaped D1 crystal with four antimers (green, yellow) in radial configuration. Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D1 symmetry, and with four antimers in radial configuration. It is a bi-isosceles triangle, and as such the two-dimensional analogue of the bi-isosceles pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Allopola Zygopleura Eutetrapleura radialia .
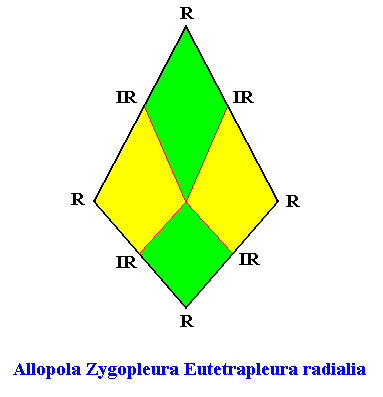
Figure above : Promorph of the above discussed two-dimensional hexagonal D1 crystal. The four antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established promorph.
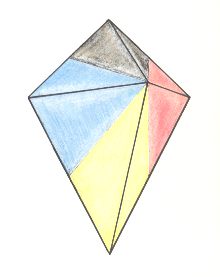
Figure above : Three-dimensional analogue of the promorph of the above discussed two-dimensional hexagonal D1 crystal : A bi-isosceles pyramid (oblique top view) with four antimers ( Allopola Zygopleura Eutetrapleura radialia ). The four antimers are indicated by colors.
D1 symmetry with three antimers.
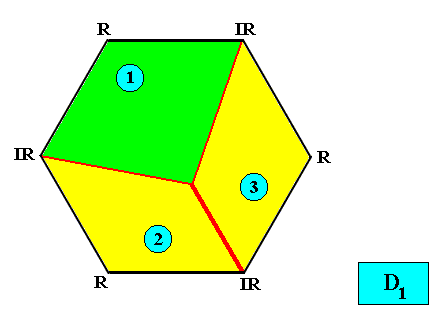
Figure above : Two-dimensional hexagon-shaped D1 crystal with three antimers (green, yellow, and indicated by numerals).
And with the Vector Rosette of Actual Growth added :
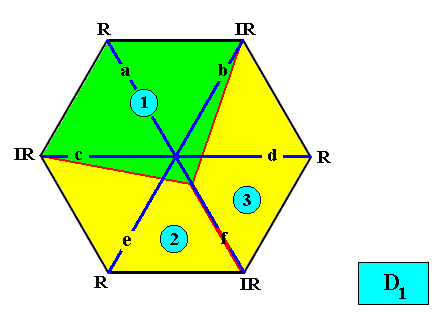
Figure above : Two-dimensional hexagon-shaped D1 crystal with three antimers (green, yellow, indicated by numerals). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D1 symmetry and with three antimers. It is half a 6-fold amphitect polygon, and as such the two-dimensional analogue of half a six-fold amphitect pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Allopola Amphipleura triamphipleura .
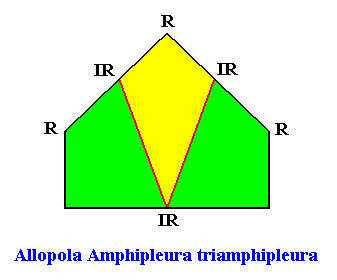
Figure above : Promorph of the above discussed two-dimensional hexagonal D1 crystal. The three antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established (two-dimensional) promorph.
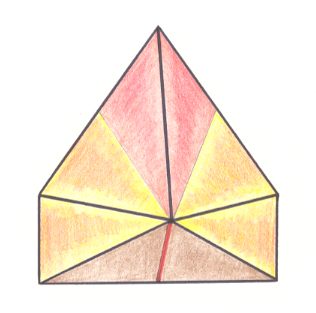
Figure above : Oblique top view of half a six-fold amphitect pyramid as the basic form of the Allopola Amphipleura triamphipleura . The three antimers are indicated by colors.
D1 symmetry with five antimers.
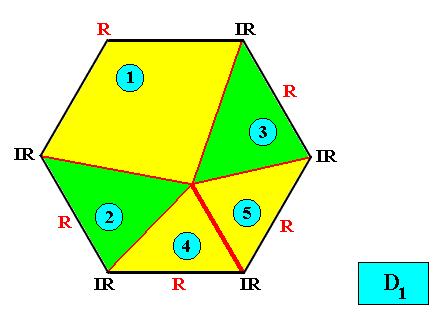
Figure above : Two-dimensional hexagon-shaped D1 crystal with five antimers (green, yellow, and indicated by numerals).
And with the Vector Rosette of Actual Growth added :
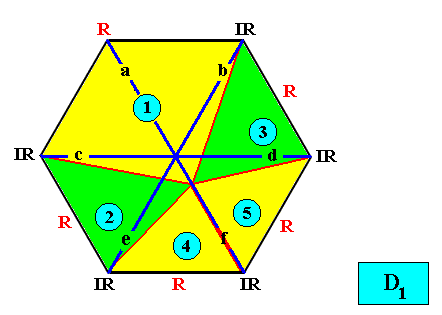
Figure above : Two-dimensional hexagon-shaped D1 crystal with five antimers (green, yellow, indicated by numerals). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D1 symmetry and with five antimers. It is half a ten-fold amphitect polygon, and as such the two-dimensional analogue of half a ten-fold amphitect pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Allopola Amphipleura pentamphipleura .
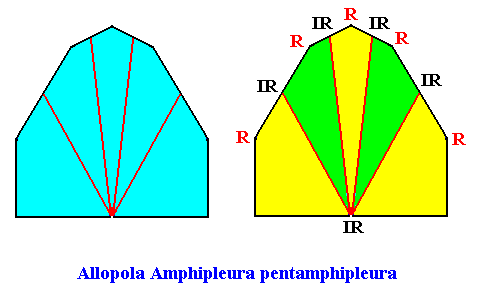
Figure above : Promorph of the above discussed two-dimensional hexagonal D1 crystal. The five antimers are indicated (green, yellow, right image).
The next Figure depicts the three-dimensional analogue of our just established (two-dimensional) promorph.
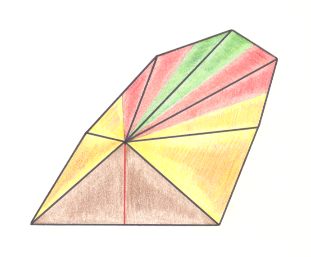
Figure above : Oblique top view of half a ten-fold amphitect pyramid as the basic form of the Allopola Amphipleura pentamphipleura . The five antimers are indicated by colors.
D1 symmetry with six antimers.
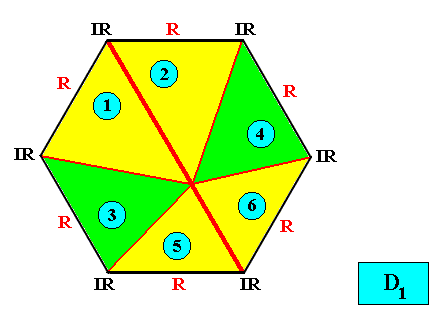
Figure above : Two-dimensional hexagon-shaped D1 crystal with six antimers (green, yellow, and indicated by numerals).
And with the Vector Rosette of Actual Growth added :
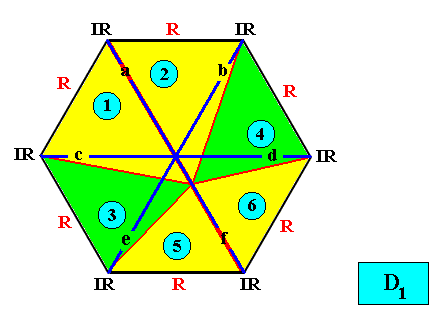
Figure above : Two-dimensional hexagon-shaped D1 crystal with six antimers (green, yellow, indicated by numerals). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic D1 symmetry and with six antimers. It is half a 12-fold amphitect polygon, and as such the two-dimensional analogue of half a 12-fold amphitect pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Allopola Amphipleura hexamphipleura .

Figure above : Promorph of the above discussed two-dimensional hexagonal D1 crystal. The six antimers are indicated (green, yellow, right image).
C2 symmetry.
The next Figure indicates the symmetry elements of an intrinsic C2 crystal.
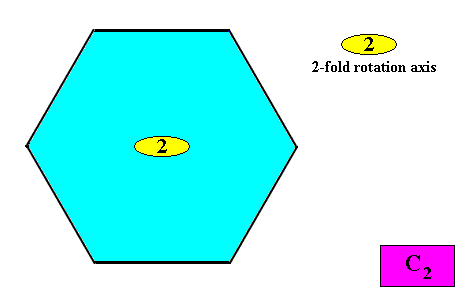
Figure above : Symmetry elements (with respect to point symmetry) of a two-dimensional crystal with intrinsic C2 symmetry : A two-fold rotation axis only.
Three crystallographic Forms are needed to conceptually construct a hexagonal crystal with intrinsic C2 symmetry :
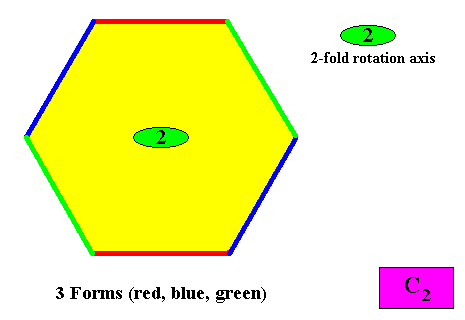
Figure above : Three crystallographic Forms are needed to conceptually construct a hexagon-shaped intrinsic C2 two-dimensional crystal : An initially given crystal face (red) implies one other face in virtue of the 2-fold rotation axis, resulting in an open Form consisting of two faces. A second initially given crystal face (blue) also implies one other face, in virtue of that same rotation axis, resulting in a second open Form also consisting of two faces. Finally, a third initially given face (green) also implies one other face and also results in an open Form consisting of two faces. The three Forms together constitute the whole hexagon-shaped crystal.
Any even number of antimers can occur in two-dimensional crystals with intrinsic C2 symmetry. Here we give some examples/
C2 symmetry and two antimers.
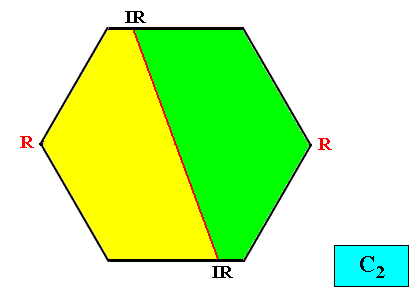
Figure above : Two-dimensional hexagon-shaped C2 crystal with two antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
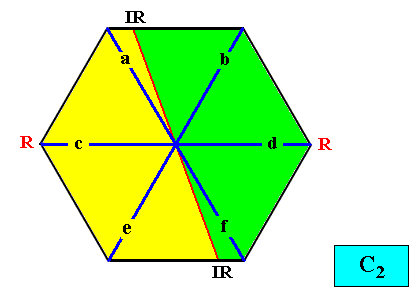
Figure above : Two-dimensional hexagon-shaped C2 crystal with two antimers (green, yellow). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic C2 symmetry and with two antimers. It is a two-fold amphitect gyroid polygon, and as such the two-dimensional analogue of a two-fold amphitect gyroid pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Heterogyrostaura dimera .
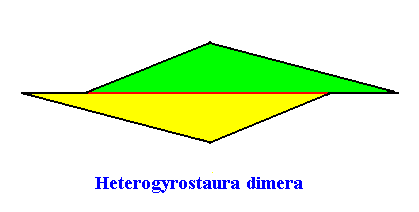
Figure above : Promorph of the above discussed two-dimensional hexagonal C2 crystal. The two antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established (two-dimensional) promorph.
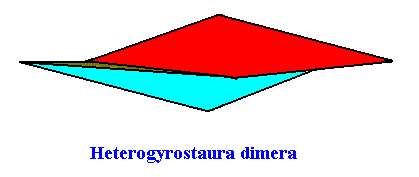
Figure above : Slightly oblique top view of a two-fold amphitect gyroid pyramid, i.e. an amphitect gyroid pyramid with two antimers, as the basic form of the Heterogyrostaura dimera . The two antimers are indicated by colors.
C2 symmetry and four antimers.
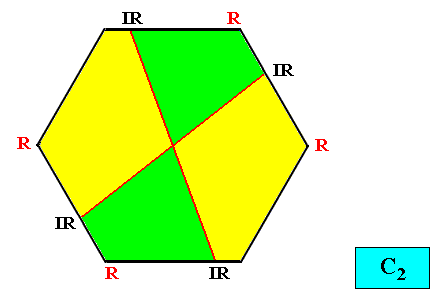
Figure above : Two-dimensional hexagon-shaped C2 crystal with four antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
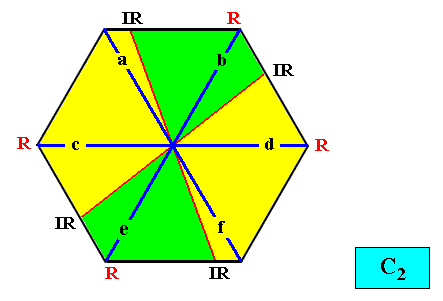
Figure above : Two-dimensional hexagon-shaped C2 crystal with four antimers (green, yellow). Vector Rosette of Actual Growth with its six vectors a, b, c, d, e, f, added.
The next Figure depicts and names the promorph of our intrinsically hexagon-shaped two-dimensional crystal with intrinsic C2 symmetry and with four antimers. It is a four-fold amphitect gyroid polygon, and as such the two-dimensional analogue of a four-fold amphitect gyroid pyramid. As promorph it is the two-dimensional analogue of an instance of the (three-dimensional) Heterogyrostaura tetramera .
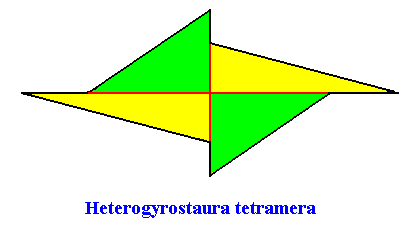
Figure above : Promorph of the above discussed two-dimensional hexagonal C2 crystal. The four antimers are indicated (green, yellow).
The next Figure depicts the three-dimensional analogue of our just established (two-dimensional) promorph.
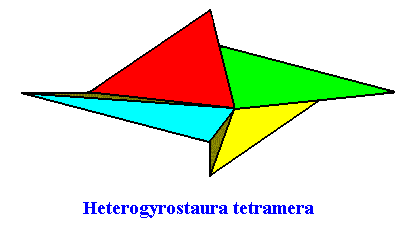
Figure above : Slightly oblique top view of a four-fold amphitect gyroid pyramid, as the basic form of the Heterogyrostaura tetramera . The four antimers are indicated by colors.
C2 symmetry and eight antimers.
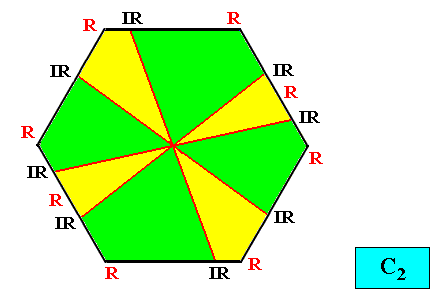
Figure above : A two-dimensional intrinsically hexagon-shaped C2 crystal with eight antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
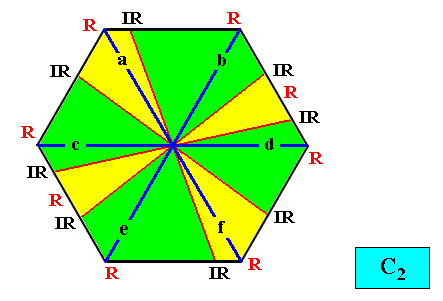
Figure above : A two-dimensional intrinsically hexagon-shaped C2 crystal with eight antimers (green, yellow). Vector Rosette of Actual Growth added.
The promorph of our two-dimensional intrinsically hexagon-shaped C2 crystal with eight antimers is depicted in the next Figure. It is an eight-fold amphitect gyroid polygon and as such the two-dimensional analogue of an eight-fold amphitect gyroid pyramid, and -- as promorph -- in turn the two-dimensional analogue of an instance of the Heterogyrostaura octomera.
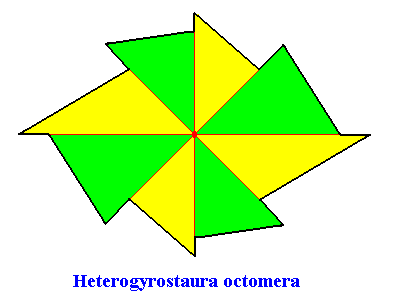
The promorphs of C2 crystals were represented here by polygons (pyramids) with receding angles. They can equally be represented by polygons (pyramids) not involving such angles, as is the case in all single crystals. But because in organisms receding angles are allowed, and because they more clearly indicate the gyroid nature of those promorphs, we prefer such angles to figure in the geometric structures representing such promorphs.
C1 symmetry and no antimers.
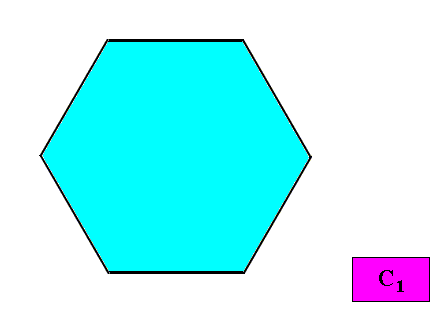
Figure above : A (two-dimensional) C1 crystal does not have any symmetry elements (with respect to point symmetry).
Six crystallographic Forms are needed to conceptually construct a two-dimensional hexagon-shaped crystal with intrinsic C1 symmetry. See next Figure.
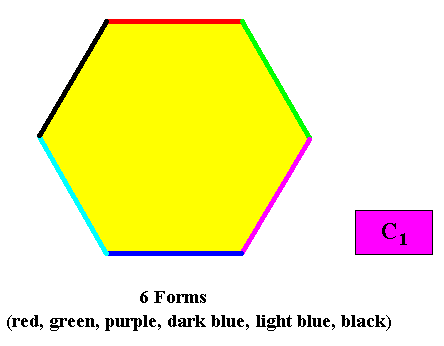
Figure above : Six crystallographic Forms are needed to construct a hexagon-shaped two-dimensional C1 crystal : Any intially given crystal face does not imply other faces. So each face is itself already a crystallographic Form. Evidently six such Forms are needed to construct a hexagon, and thus the whole hexagon-shaped C1 crystal.
C1 crystals cannot have genuine antimers. See next Figures.
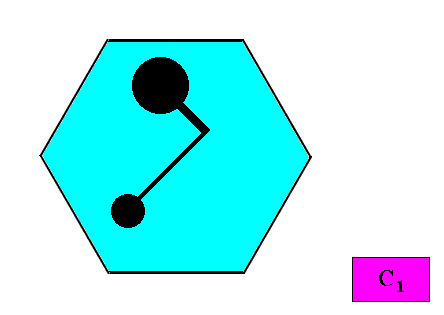
Figure above : A two-dimensional intrinsically hexagon-shaped C1 crystal.
A motif (black) is inserted to express the crystal's C1 symmetry.
And with the Vector Rosette of Actual Growth added :
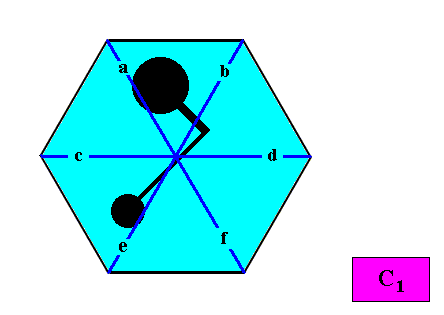
Figure above : A two-dimensional intrinsically hexagon-shaped C1 crystal. A motif (black) is inserted to express the crystal's C1 symmetry. Vector Rosette of Actual Growth added. All vectors a, b, c, d, e, f, are unique (i.e. non-equivalent).
The next Figure (two images) gives the possible promorphs (and their names) of our hexagon-shaped C1 crystal. The promorph is either (left image) half an isosceles triangle (and, equivalently, a quarter of a rhombus), and is as such the two-dimensional analogue of a quarter of a rhombic pyramid, or (right image) an irregular triangle, indicating two unequal antimers (yellow, green), and is as such the two-dimensional analogue of an irregular pyramid (or, equivalently, a 1-fold pyramid).
This concludes our investigation of promorphs as they can occur in two-dimensional crystals of the following intrinsic shapes : Rectangle, Square, Parallelogram, Rhombus, Equilateral Triangle and Regular Hexagon.
While the foregoing documents investigated promorphs of two-dimensional crystals from the view point of their intrinsic shape , the next document will summarize the results -- two-dimensional crystals of certain shapes and their possible promorphs -- under the view point of promorph , before continuing to investigate other intrinsic shapes of two-dimensional crystals with respect to their possible promorphs.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XV.
e-mail : 