

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Square (Promorphs)
The Vector Rosette of Actual Growth of a quadratic crystal, i.e. of any two-dimensional crystal having (when fully developed) its intrinsic shape to be that of a square (which, all by itself has D4 symmetry), and (such a crystal) of whatever (possible) intrinsic symmetry, is then as follows (blue lines) :
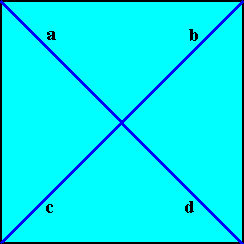
This vector rosette, viz. a vector rosette of a square 2-D crystal, in fact consists of four lines, a, b, c, d, each originating in the center of the crystal and ending up at a corner. As such it encodes the crystal's shape. And the lines of this rosette generally point to the presence of four antimers where, of course, in addition to these four lines, also the boundaries between the antimers indicate special directions, as well as the mirror lines, if present, of the crystal (which can coincide with the boundaries between antimers, or coincide with the median lines of antimers).
D4 symmetry ( Point symmetry, see (bottom of) Table of Plane groups, supporting square crystals, Part VII ).
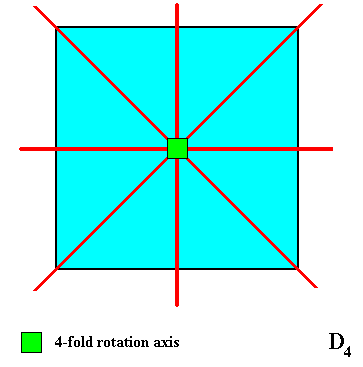
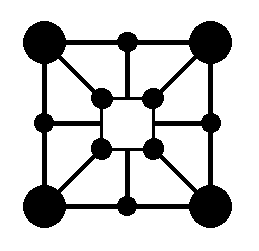
The D4 symmetry of the square crystal (as a first case of possible intrinsic point symmetry of a square two-dimensional crystal) is indicated in the next Figure by the pattern of symmetry elements [rotation axis (green), reflection lines (red)].
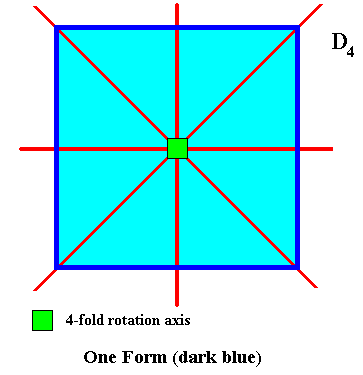
The square shape of the D4 crystal can be (conceptually) generated by just one Form (in the crystallographic sense) : one initial crystal face, parallel to one of the mirror lines, automatically implies three more faces, together constituting one crystallographic Form -- a square, in virtue of the symmetry elements. And this one Form is already constituting the whole (square) shape of our crystal :
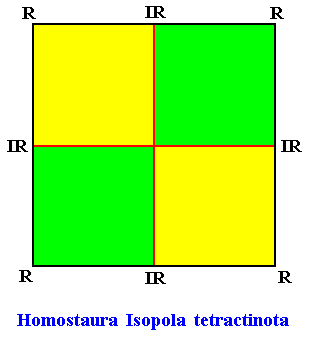
D4 symmetry and four antimers.
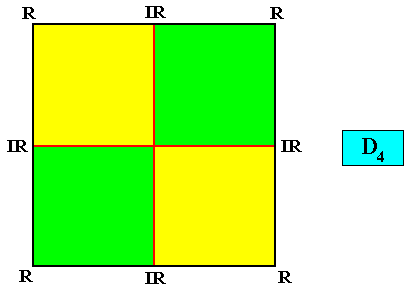
Figure above : A two-dimensional intrinsically quadratic crystal with intrinsic D4 symmetry with its four antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
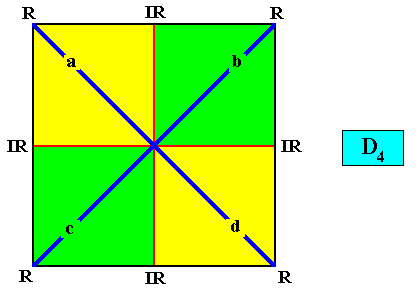
As before, in the drawings the radial directions are indicated by R , while the interradial directions are indicated by IR . The assignment of them, in the sense of a direction either to be radial or interradial, is arbitrary in the case of purely mathematical images (figures), but relevant in biology, where radial directions are associated with conspicuous morphological features or spatial extensions in those directions (think of tentacles of polyps or arms of star-fishes). In crystals such an assignment is more or less arbitrary, depending on the morphology of the chemical motif. We shall agree on the median lines of antimers to be radial directions, while the lines separating adjacent antimers are considered to be interradial.
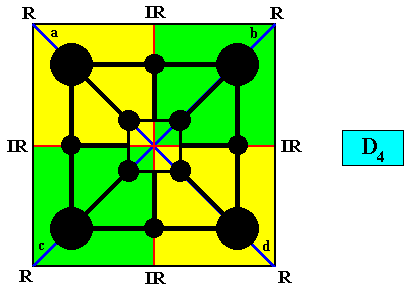
In order to illustrate what, in the present case, makes the four vectors of the vector rosette of our square crystal equivalent, we insert the following motif compatible with the intrinsic symmetry of the crystal :
The next Figure is the same as was depicted above (showing the four antimers), but now with this motif (which as such is then a motif s.str.) (black) inserted, in order to show the equivalence of all four vectors a, b, c, d of the vector rosette as depicted earlier .
To see in what way the motif (shown by a comparable motif, also having D4 symmetry) is actually only microscopically present (and then periodically repeated) in the square crystal, see the relevant Figure in Part VII . Sometimes such a motif is 'smeared out' as it were because of glide reflections (of which only the reflection component is macroscopically visible, because the translations are very small). When, in addition to the simple translations, also the translational component of such glide reflections is eliminated (turning them into ordinary reflections, which is what we do when looking to the crystal macroscopically), we are, in the present case, left with a translation-free residue with D4 symmetry. See for this latter case the relevant Figure in Part VII .
The next Figure depicts and assesses the promorph of our square crystal, which (crystal) has, in the present case, a D4 intrinsic point symmetry. This promorph turns out to be the 2-D (i.e. two-dimensional) analogue of a quadratic pyramid (i.e. a regular 4-fold pyramid, or pyramid with a square as its base), which has four antimers (green, yellow) [ The group describing the symmetry of our 2-D promorph (a square) is isomorphic with the group describing the symmetry of the quadratic pyramid (which is a 3-D promorph)].
C4 symmetry and four antimers.
Also for a square crystal with point symmetry C4 one crystallographic Form can represent the shape of such a crystal. An initial crystal face implies three more faces in virtue of the 4-fold rotation axis, together constituting one crystallographic Form, which can represent the whole crystal. See next Figure.
The next Figure depicts an example of the four antimers of our square crystal with intrinsic C4 point symmetry.
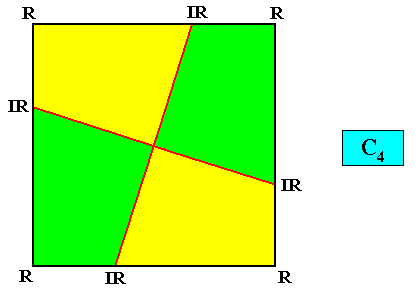
Figure above : A two-dimensional intrinsically quadratic crystal with intrinsic C4 symmetry and its four antimers (green, yellow).
And with the Vector Rosette of Actual Growth added :
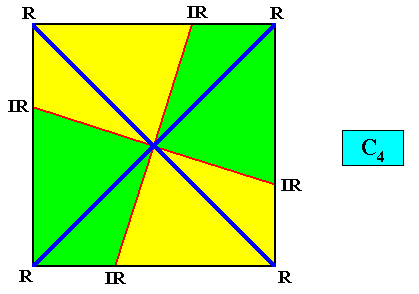
Again, in order to (better) illustrate what, in the present case (C4 ), makes the four vectors of the vector rosette of our square crystal equivalent, we insert the following motif compatible with the intrinsic symmetry (C4 ) of the crystal :
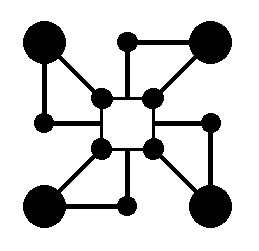
The next Figure is the same as was depicted above (showing the four antimers), but now with this motif (which as such is then a motif s.str.) (black) inserted, in order to show the equivalence of all four vectors a, b, c, d of the vector rosette as depicted earlier .
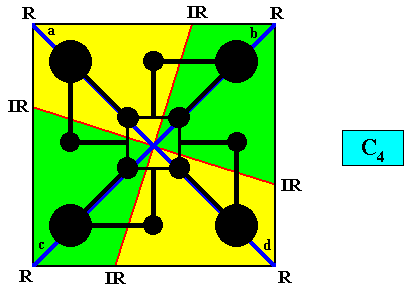
To see in what way the motif (shown by a comparable motif, also having C4 symmetry) is actually only microscopically present (and then periodically repeated) in the square crystal, see the relevant Figure in Part VII .
The next three Figures are about the promorph (and its name) of our square crystal with its intrinsic C4 point symmetry.
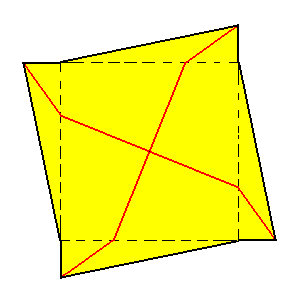
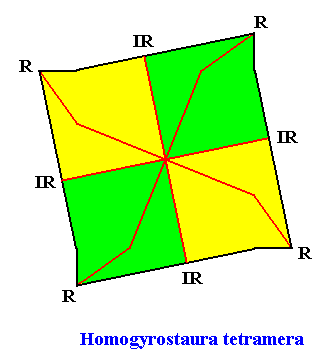
Figure above : Base of a regular gyroid pyramid with four antimers. The 4-fold rotation axis (main axis) is perpendicular to the plane of the drawing and goes through the center of the image. The two s i g m o i d radial cross axes are shown in red. Their shape, as drawn, only symbolizes their sigmoid character.
The following Figure gives, for clarity, the three-dimensional version of a promorph representing the Homogyrostaura tetramera.
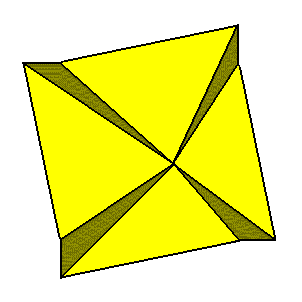
Figure above : Slightly oblique top view of a regular gyroid pyramid with four antimers ( Homogyrostaura tetramera). The group, representing the symmetry (C4) of this regular four-fold gyroid pyramid is isomorphic to that representing the symmetry of its base alone, i.e. of (any) regular four-fold gyroid polygon.
Alternatively, the promorph of our square crystal with intrinsic C4 point symmetry can be given by a figure without receding angles :
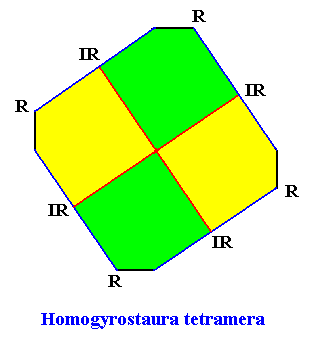
Figure above : Alternative expression of the promorph representing the (2-D analogue of the) Homogyrostaura tetramera (C4 promorph). The geometric image, expressing the promorph has no receding angles (as they also do not occur in single crystals).
D2 symmetry.
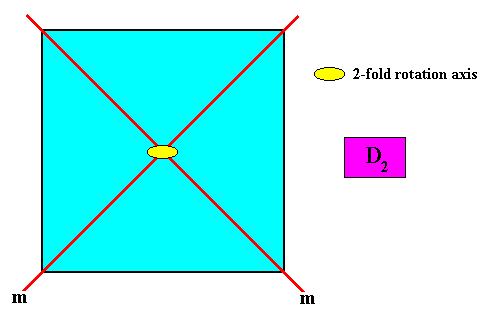
Figure above : Symmetry elements of a square (quadratic) crystal having D2 intrinsic point symmetry : One 2-fold rotation axis (small yellow solid ellipse) and two diagonal mirror lines ( m ).
To generate crystal faces, together forming a square, i.e. to generate a square D2 crystal, takes one crystallographic Form only : An initial face at 450 to a mirror line implies three new faces in virtue of the two mirror lines. The new faces plus the initial one, together constituting one crystallographic Form, viz. a square, thus form the whole crystal. See next Figure.
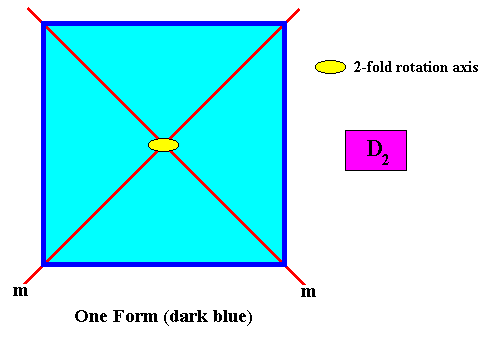
Figure above : To generate a square two-dimensional crystal with point symmetry D2 , only one crystallographic Form (dark blue) is needed.
D2 symmetry and four antimers.
The next Figure depicts the four antimers (yellow, green) and the Vector Rosette of Actual Growth (four vectors, indicated as dark blue lines) of a square crystal with intrinsic D2 symmetry.
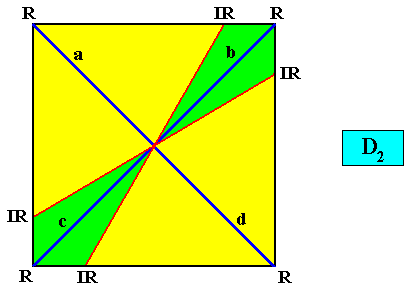
Figure above : The four antimers (two-by-two unequal) and the Vector Rosette of Actual Growth (blue lines, a, b, c, d ) of a two-dimensional square crystal with intrinsic D2 point symmetry. The two-by-two unequality of the antimers demonstrates the two-by-two non-equivalence of the (four) vectors ( a, b, c, d ) of the rosette. The configuration of the four antimers is r a d i a l because the mirror lines, which are perpendicular to each other and as such point to the directional axes of the promorph, run right through the antimers.
The next Figure is the same, but without the vector rosette.
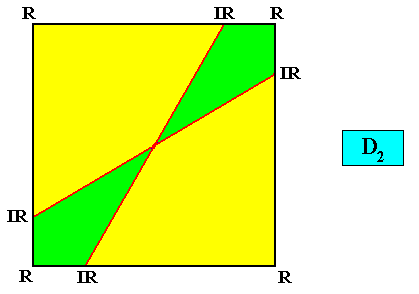
Figure above : The four antimers (two-by-two unequal) of a two-dimensional square crystal with intrinsic D2 point symmetry.
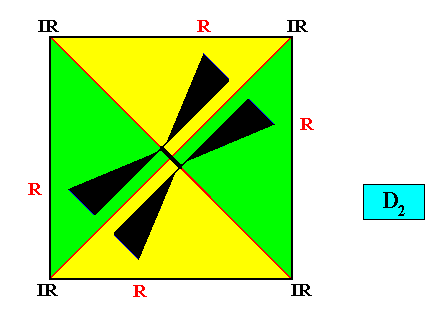
The next Figure again depicts our crystal under investigation (square, D2 , four antimers), but now with a (compatible) motif s.str. (black) inserted (itself consisting of four antimers, two-by-two unequal), in order to emphasize and represent the crystal's intrinsic D2 point symmetry and so emphasizing the two-by-two unequality of the antimers that causes the two-by-two non-equivalence of the four vectors ( a, b, c, d ) of the vector rosette and at the same time causes the absence of horizontal and vertical mirror lines.
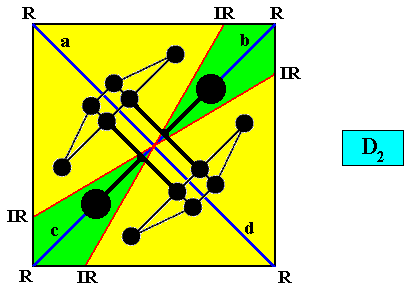
Another possible compatible motif, showing perhaps more clearly the number and configuration of the four antimers, could be as follows :
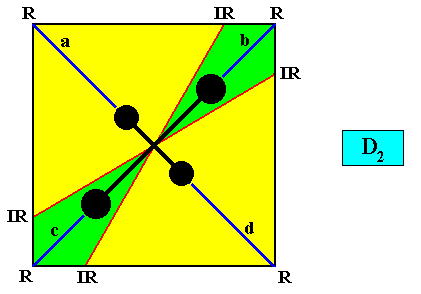
While in the above Figures we had a radial configuration of four antimers, in the next Figure we illustrate an interradial configuration of four antimers :
To see in what way the motif (shown by a comparable motif, also having D2 symmetry) is actually only microscopically present (and then periodically repeated) in the square crystal, see the relevant Figure in Part VII . Sometimes such a motif is 'smeared out' as it were because of glide reflections (of which only the reflection component is macroscopically visible, because the translations are very small). When, in addition to the simple translations, also the translational component of such glide reflections is eliminated (turning them into ordinary reflections, which is what we do when looking to the crystal macroscopically), we are, in the present case, left with a translation-free residue with D2 symmetry. See for this latter case the relevant Figure in Part VII .
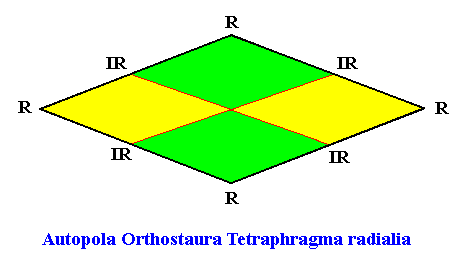
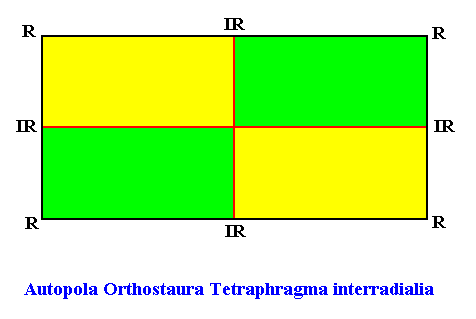
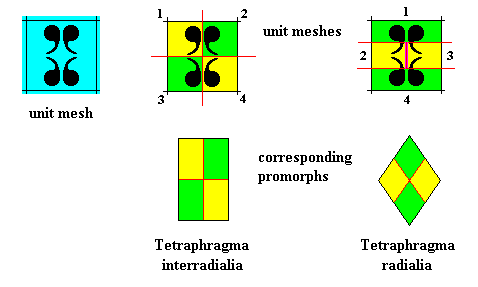
The next two Figures, finally, depict the promorph of our quadratic crystal with intrinsic D2 point symmmetry and four antimers. It can either be the 2-D analogue of a rhombic pyramid (in fact it is its base) with four antimers (yellow, green) :
The next Figure explains these two promorphological possibilities. They depend on how the motif lets itself be interpreted in terms of antimers.
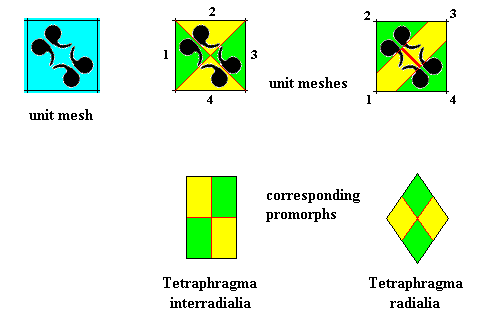
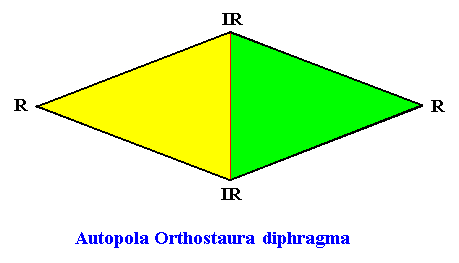
Figure above : The chemical and morphological features of a two-dimensional ('chemical') D2 motif determine which parts of it to be interpreted as antimers. In the case of a motif consisting of four antimers the promorph can then be either that of the (Autopola Orthostaura) Tetraphragma interradialia, or that of the (Autopola Orthostaura) Tetraphragma radialia. The spatial configuration of the four antimers (green, yellow, and indicated by numerals) is different in each case (See for this difference also our Promorphological System of Stereometric Basic Forms (Promorphs) at "Autopola" in Second Part of Website : BASIC FORMS ).
For an explanation of directional axes and their being radial or interradial see above and also HERE in Part VI .
The delineation of the four antimers can be indicated in several equivalent ways. The next Figure shows this for the radial configuration.
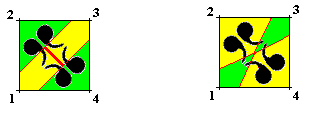
The next Figure illustrates the same as the last-but-one, but now for the case of the two mirror lines being non-diagonally oriented (a case, considered further below).
Also here the delineation of the four antimers can be indicated in several equivalent ways. The next Figure shows this for the radial configuration.
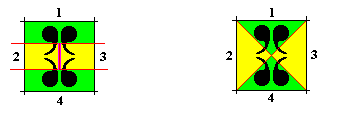
D2 symmetry and two antimers.
A two-dimensional, intrinsically square crystal, with intrinsic D2 symmetry, can, in some cases, possess only two antimers instead of four. See next Figure.
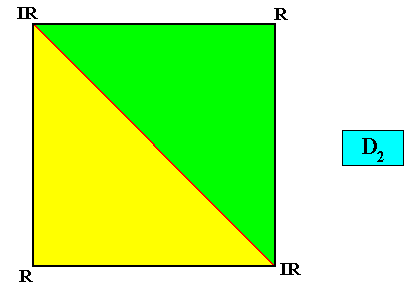
Figure above : A two-dimensional square crystal, having D2 symmetry and (only) two antimers (yellow, green).
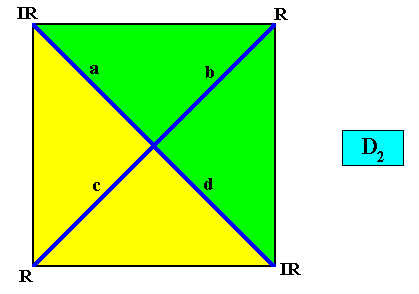
To emphasize the crystal's D2 intrinsic symmetry and (to emphasize) the non-equivalence of the vectors a and b and of the vectors c and d (while a is equivalent to d , and b is equivalent to c ), we insert a motif (black), itself having D2 symmetry (as such representing the crystal's point symmetry), but clearly having only two antimers. See next Figure.
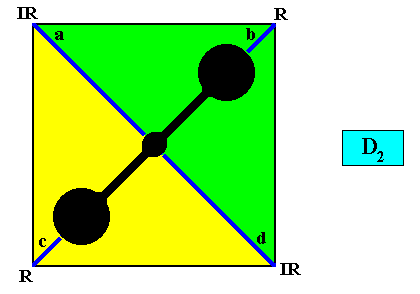
Figure above : Same as previous Figure, but now with a D2 motif inserted, representing the crystal's point symmetry and indicating the two antimers.
The next Figure gives the promorph (and its name) of the above square D2 crystal with two antimers.
D2 symmetry and six antimers.
A two-dimensional, intrinsically square crystal, with intrinsic D2 symmetry, can, in some cases, possess six antimers . See next Figure.
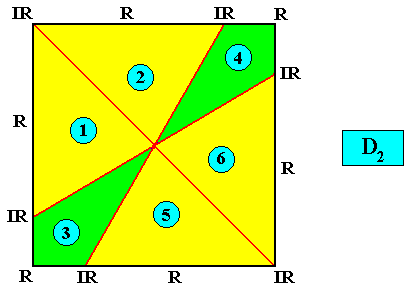
Figure above : Two-dimensional square crystal with intrinsic D2 symmetry and six antimers (green, yellow), indicated by the numerals 1, 2, 3, 4, 5 and 6.
The next Figure is the same as the previous one, but with the symmetry elements (one 2-fold rotation axis (small solid dark blue ellipse) and two mirror lines (red)) inserted.
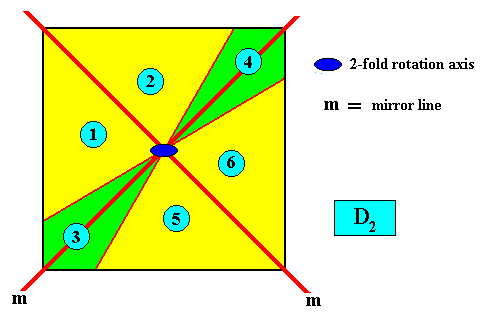
In the next Figure the Vector Rosette of Actual Growth, with its four vectors a, b, c, d , is indicated (dark blue lines).
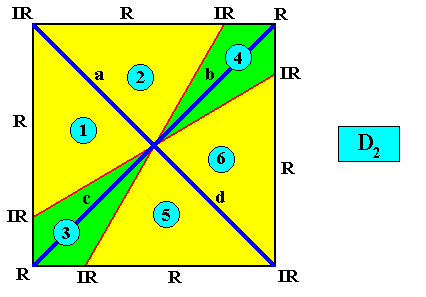
Figure above : Two-dimensional square crystal with intrinsic D2 symmetry and six antimers. The Vector Rosette of Actual growth is indicated (blue lines).
The next Figure, finally, gives the promorph (and its name) of our crystal.
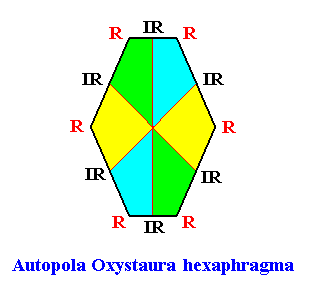
Figure above : Promorph of the two-dimensional square crystal considered above (D2 , six antimers). It is a six-fold amphitect polygon and as such the two-dimensional analogue of a six-fold amphitect pyramid.
In the foregoing we considered d i a g o n a l mirror lines to be present in a square crystal with intrinsic point symmetry D2 . They represented the two (only) mirror lines of any D2 object. But of course the two mirror lines of D2 symmetry could, alternatively, be represented by the two non-diagonal mirror lines of the square crystal (Where then the diagonals would not be mirror lines). And because a minimum of crystallographic Forms (namely one) are needed to construct a D2 crystal if its two mirror lines coincide with the diagonals of the square, we started considering this case. And now it is time to consider the other case as well.
The next Figure indicates the pattern of symmetry elements of such a crystal.
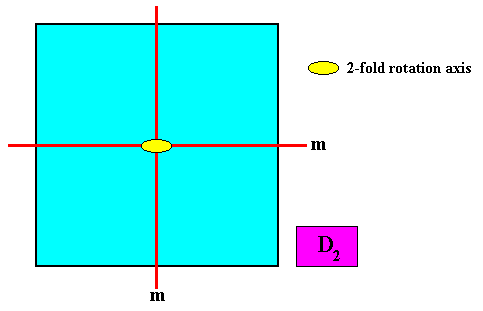
Figure above : Symmetry elements of a two-dimensional intrinsically square crystal with intrinsic D2 point symmetry : One 2-fold rotation axis and two mirror lines ( m ) intersecting at the piercing point of the rotation axis. The two mirror lines do not coincide with the diagonals of the square.
Two crystallographic Forms are needed to mentally construct such a crystal : An initial crystal face parallel to one of the mirror lines (and perpendicular to the other) implies a second face in virtue of either the 2-fold axis or the parallel mirror line. No further faces can be developed, so these two faces (two parallel faces) together constitute a crystallographic Form. And because it is an open Form, it cannot represent a crystal. In order to do so it must combine with another Form resulting in a closed figure. So a second initial face is needed, one perpendicular to the first one. And this second initial face implies another face parallel to it in virtue of the 2-fold rotation axis or the mirror line parallel to it, and resulting in a second Form. Combining these two Forms yields four faces forming a square and representing in this way the whole (two-dimensional) crystal. See next Figure.
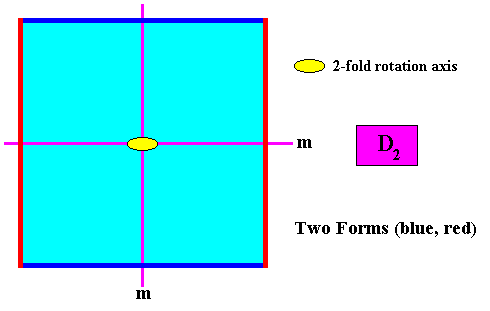
Figure above : The two Forms (blue, red) of a two-dimensional square crystal with intrinsic D2 symmetry and non-diagonal mirror lines.
With such a crystal, i.e. with a square crystal having D2 symmetry, we consider again the case of four antimers.
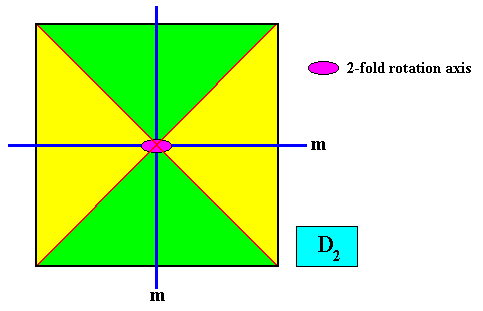
Figure above : The four antimers (green, yellow) of a square D2 crystal with non-diagonal mirror lines. Symmetry elements indicated. All figures with D2 symmetry have two (and no more than two) mirror lines perpendicular to each other. And because they are perpendicular, they must correspond with the directional axes of the corresponding promorphs of such D2 figures. In the crystal of the present Figure we can see that these (directional) axes are radial (because they coincide with the median lines of the antimers [geen, yellow]), and so the corresponding promorph must also be radial.
A second possible configuration of the four antimers is the interradial configuration :
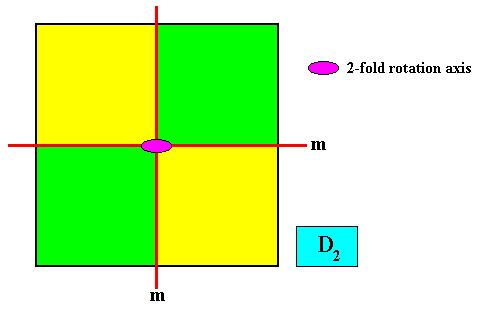
Figure above : The four antimers (green, yellow) of a square D2 crystal with non-diagonal mirror lines. Symmetry elements indicated. The antimers correspond to the corner areas of the square, and their configuration is interradial, because the mirror lines, necessarily representing to the promorphological directional axes, are interradial ( They run between antimers).
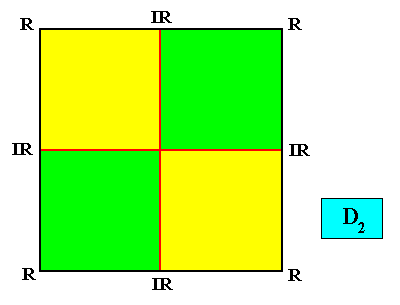
Figure above : Same as previous Figure : The four antimers (green, yellow) of a square D2 crystal with non-diagonal mirror lines. Symmetry elements not drawn. Radial (R) and interradial (IR) directions indicated. Configuration of the four antimers interradial.
The next Figure indicates the Vector Rosette of Actual Growth of our square crystal.
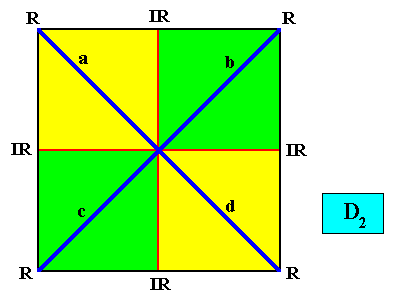
Figure above : Same as previous Figure : The four antimers (green, yellow) of a square D2 crystal with non-diagonal mirror lines. Vector Rosette of Actual Growth with its four vectors a, b, c, d indicated (dark blue lines).
The above three Figures are, however only partially adequate, because they suggest that each antimer is in itself mirror symmetric, and that they relate to each other by a 4-fold rotation axis. All this cannot be, because it is not compatible with the pattern of symmetry elements in these three Figures. In order to express the true nature of the four antimers we insert a motif :
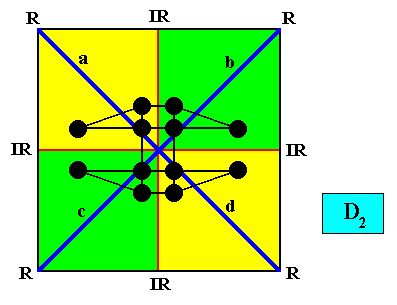
Figure above : Same as previous Figure. Motif (black) inserted in order to highlight the D2 intrinsic symmetry of the crystal (i.e. the intrinsic point symmetry of the crystal is not that of its quadratic shape, which is D4 ). Compare with the quadratic crystal with intrinsic D4 symmetry, considered above . Compare also with the quadratic D2 crystal with its two mirror lines coinciding with the diagonals of the square, also considered above . The configuration of the four antimers is interradial.
The next Figure shows the second configuration, mentioned earlier, viz. the radial configuration of the four antimers, elucidated by an inserted motif (black).

Figure above : A two-dimensional intrinsically square crystal with intrinsic point symmetry according to the group D2 , and having four antimers (green, yellow). Radial configuration of antimers, indicated by an inserted motif (black), which also expresses the D2 intrinsic symmetry of the crystal.
To see in what way the motif (shown by a comparable motif, also having D2 symmetry) is actually only microscopically present (and then periodically repeated) in the quadratic crystal, see the relevant Figure in Part VII . Sometimes such a motif is 'smeared out' as it were because of glide reflections (of which only the reflection component is macroscopically visible, because the translations are very small). When, in addition to the simple translations, also the translational component of such glide reflections is eliminated (turning them into ordinary reflections, which is what we do when looking to the crystal macroscopically), we are, in the present case, left with a translation-free residue with D2 symmetry. See for this latter case the relevant Figure in Part VII .
The promorph of our quadratic D2 crystal with non-diagonal mirror lines and four antimers is the same (viz. (Autopola Orthostaura) Tetraphragma radialia or interradialia ) as that of the quadratic D2 crystal with diagonal mirror lines (i.e. with its only two mirror lines being diagonal) and four antimers, as considered above .
D2 symmetry with two antimers.
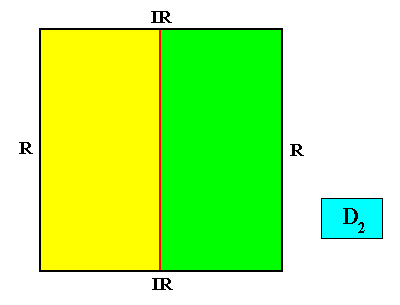
Figure above : The (case of having only) two antimers (green, yellow) of a quadratic D2 crystal with its two mirror lines non-diagonally positioned.
And with the Vector Rosette of Actual Growth added :
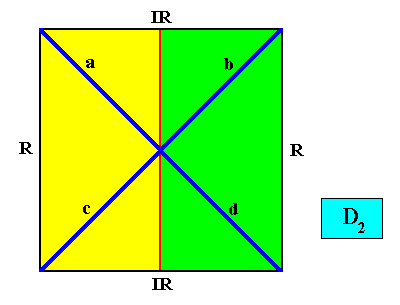
Figure above : The (case of having only) two antimers (green, yellow) of a quadratic D2 crystal with its two mirror lines non-diagonally positioned. Vector Rosette of Actual Growth added. All vectors, a, b, c, d are equivalent.
The promorph of an intrinsically quadratic two-dimensional crystal with intrinsic D2 symmetry and two antimers, and having its mirror lines non-diagonally positioned, i.e. the crystal just discussed, is the same as that of precisely such a crystal, but having its mirror lines diagonally positioned. This promorph was depicted above .
D2 symmetry and six antimers.
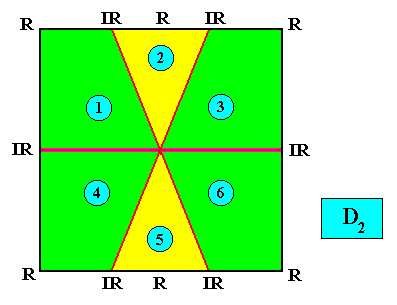
Figure above : The six antimers (green, yellow) of a quadratic D2 crystal with its two mirror lines non-diagonally positioned. The antimers are (also) indicated by numerals.
The next Figure adds the Vector Rosette of Actual Growth :
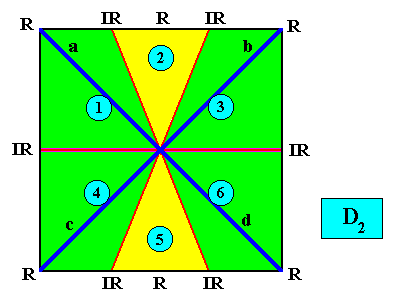
Figure above : The six antimers (green, yellow) of a quadratic D2 crystal with its two mirror lines non-diagonally positioned. The antimers are (also) indicated by numerals. The Vector Rosette of Actual Growth with its four vectors a, b, c, d is indicated (blue lines). All four vectors are equivalent. Compare with the quadratic D2 crystal, also with six antimers, but with its mirror lines in a diagonal position, considered above .
The promorph of such a crystal, i.e. of an intrinsically quadratic D2 crystal with its mirror lines non-diagonally positioned and with six antimers, is the same as that of an intrinsically quadratic crystal, also with intrinsic D2 symmetry, and also with six antimers, but with its mirror line diagonally positioned. This promorph was depicted above .
D1 symmetry.
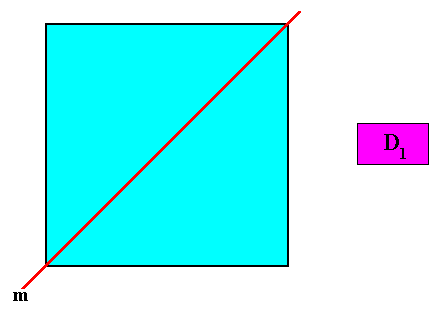
Figure above : The only symmetry element (with respect to point symmetry) -- a mirror line ( m ) -- of a square crystal with intrinsic D1 point symmetry.
To generate the whole crystal conceptually, two crystallographic Forms are needed : An initial crystal face at 450 to the mirror line implies a second face (in virtue of this mirror line). The so obtained face pair is a Form (an open Form). A face perpendicular perpendicular to the first one also implies a second face (in virtue of the mirror line). The so obtained face pair is another Form (also an open Form). The two Forms together constitute a square, and thus represent the whole crystal. See next Figure.
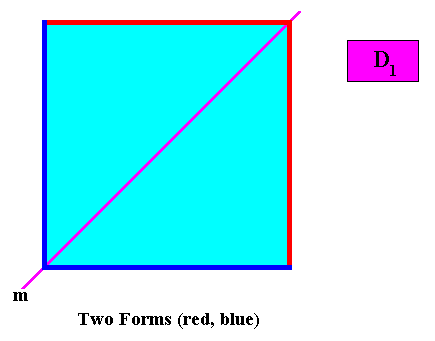
A crystal with intrinsic D1 symmetry in principle admits of any number (> 1) of antimers, as long as they are symmetrically arranged with respect to a mirror line. We give some examples.
D1 symmetry and two antimers.
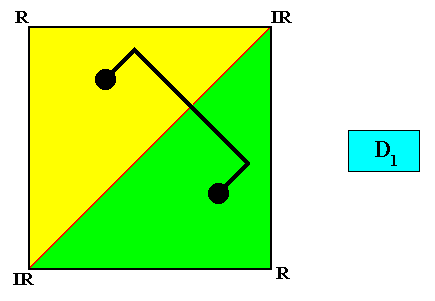
Figure above : Two-dimensional, and intrinsically square crystal, with point symmetry D1 and two antimers (green, yellow). A motif (black) is added to indicate that there is only one mirror line present.
The next Figure is the same as the previous one, but now provided with the crystal's Vector Rosette of Actual Growth, with its four vectors a, b, c, d . The inserted motif (black) demonstrates the non-equivalence of a and c , of b and d , of c and d , of b and c and, finally, also of a and b , and it demonstrates the equivalence of a and d . Further it expresses the intrinsic D1 point symmetry of the crystal (despite its intrinsic square shape).
To see in what way the motif (shown by a comparable motif, also having D1 symmetry) is actually only microscopically present (and then periodically repeated) in the square crystal, see the relevant Figure in Part VII . Sometimes such a motif is 'smeared out' as it were because of glide reflections (of which only the reflection component is macroscopically visible, because the translations are very small). When, in addition to the simple translations, also the translational component of such glide reflections is eliminated (turning them into ordinary reflections, which is what we do when looking to the crystal macroscopically), we are, in the present case, left with a translation-free residue with D1 symmetry. See for this latter case the relevant Figure in Part VII .
The next Figure gives and names the promorph of our intrinsically quadratic D1 two-dimensional crystal with its mirror line (as an element of its point group) coinciding with a diagonal of the square, and with two antimers.
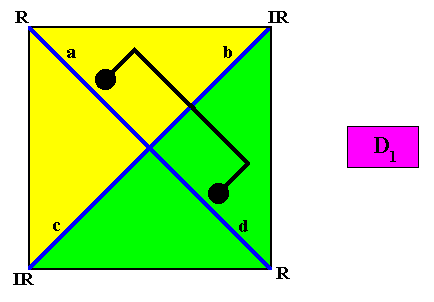
D1 symmetry and four antimers.
Figure above : Two-dimensional quadratic D1 crystal, with four antimers. The inserted motif (black) clearly shows which lines are going to represent the directional axes of the promorph : One of them is the mirror line (coincident with the NE diagonal, see Figure above ), the other is perpendicular to it (and is not a mirror line). And we see that these lines run between antimers, so the configuration of the antimers is interradial.
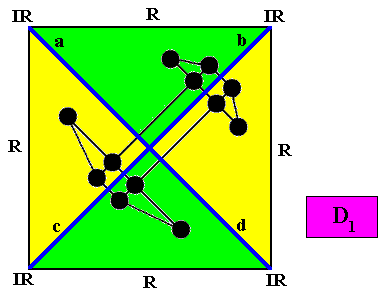
Figure above : Same as previous Figure. Vector Rosette of Actual growth with its four vectors a, b, c, d added.
The four antimers allow for two types of configuration. One type we have just depicted, viz. the interradial configuration. It promorphologically corresponds to the (Allopola Zygopleura) Tetrapleura interradialia, while a second type promorphologically corresponds to the (Allopola Zygopleura) Tetrapleura radialia . See for this second type of configuration of the four antimers, the next two Figures.
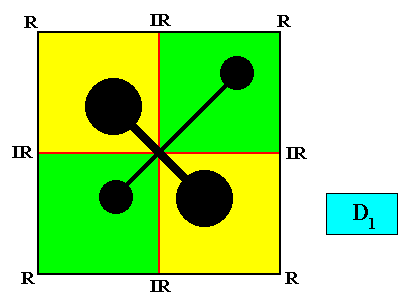
Figure above : Two-dimensional quadratic D1 crystal, with four antimers. Alternative configuration (viz. radial) of the four antimers. Also here the inserted motif expresses the intrinsic symmetry and shows where the lines that are going to represent the directional axes of the promorph are to be found : NE diagonal mirror line and the line perpendicular to it, and they are radial.
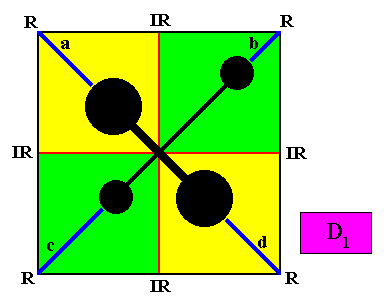
Figure above : Same as previous Figure. Vector Rosette of Actual growth with its four vectors a, b, c, d added.
As has been noted earlier, the motif (black) in the above figures does not as such occur in a crystal. It here only serves to indicate the intrinsic D1 point symmetry of the crystal, as caused by comparable microscopic motifs, which, as translation-free residues of the relevant plane group, represent the crystal's point symmetry.
The next Figures give and name the promorphs respectively possessed by the two types (radial, interradial) of quadratic D1 crystal with diagonal mirror line (One can see that whether the mirror line is diagonal or non-diagonal does not make a difference in promorph) :
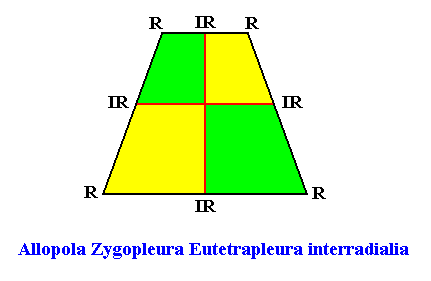
Figure above : Promorph of the quadratic D1 crystal with four antimers. It is an isosceles trapezium, and as such a two-dimensional analogue of the trapezoid pyramid (i.e. it is its base). The four antimers (green, yellow) and the radial and interradial directions are indicated. The configuration of the antimers is interradial.
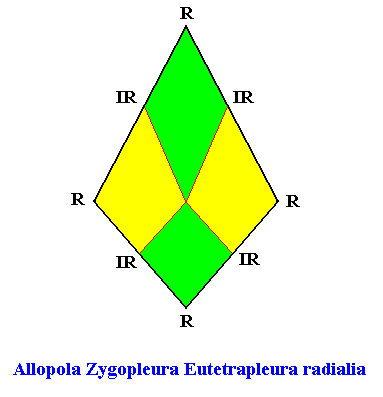
Figure above : Promorph of the quadratic D1 crystal with four antimers. Alternative configuration (viz. radial) of the four antimers. This promorph is a bi-isosceles triangle, and as such the two-dimensional analogue of the bi-isosceles pyramid (i.e. it is its base). The four antimers (green, yellow) and the radial and interradial directions are indicated.
As we did already in Part VI (concerning rectangular crystals), the next three Figures elaborate a little more on the directional axes of D1 promorphs (Allopola) with four antimers ( Allopola Zygopleura eutetrapleura, in fact, their two-dimensional analogues). The two possible promorphs were given just above.
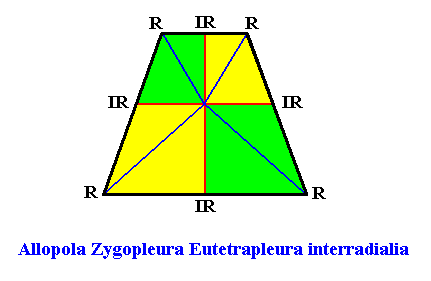
Figure above : Cross axes (two pairs, blue, red) of the isosceles trapezium, the basic form of the Eutetrapleura interradialia. The perpendicular cross axes (red) are the directional axes, while the other axes (blue) are just ordinary cross axes. The latter are bent, but this is neither typical, nor necessary as the next Figure shows.
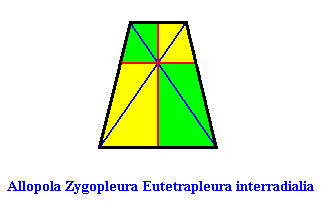
Figure above : Cross axes of the isosceles trapezium, the basic form of the Eutetrapleura interradialia. Two sets of (straight) cross axes (red, blue). The perpendicular ones (red) are the directional axes of the isosceles trapezium. The horizontal directional axis does not connect the centers of opposite sides, but this is to be expected because of the absence in the promorph of a horizontal mirror line.
Also the basic form of the Allpola Zygopleura Eutetrapleura r a d i a l i a can be depicted by a polygon, viz. a bi-isosceles triangle, such that it has straight cross axes :
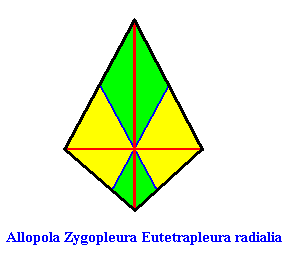
Figure above : Cross axes of a bi-isosceles triangle, the basic form of the Eutetrapleura radialia. All cross axes are straight. The perpendicular ones (red) are the directional axes of the bi-isosceles triangle.
D1 symmetry and six antimers.
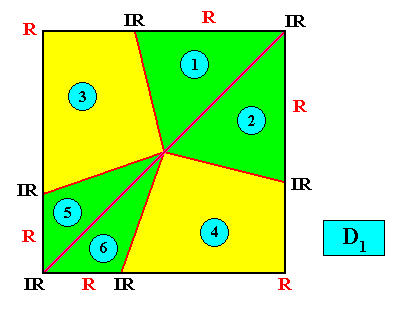
Figure above : A two-dimensional quadratic D1 crystal with six antimers (green, yellow). The six antimers are indicated by numerals.
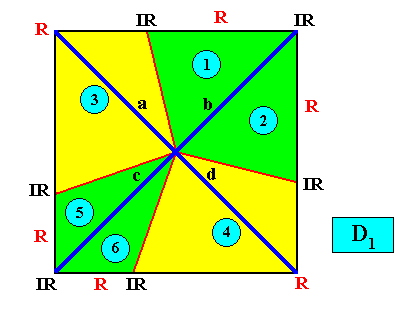
Figure above : Same as previous Figure : a two-dimensional quadratic D1 crystal with six antimers (green, yellow). The Vector Rosette of Actual Growth, with its four vectors a, b, c, d indicated (blue lines).
The next Figure gives (with two images) the promorph (and its name) of the above quadratic crystal ( D1 , six antimers). It is half a 12-fold amphitect polygon, and as such a two-dimensional analogue of half a 12-fold amphitect pyramid (i.e. it is its base). In the right image the six antimers (green, yellow) and the radial and interradial directions are indicated.
The next Figure is the same, but with the median lines of the antimers omitted, in order to let the latter come out more clearly.

D1 symmetry and three antimers.
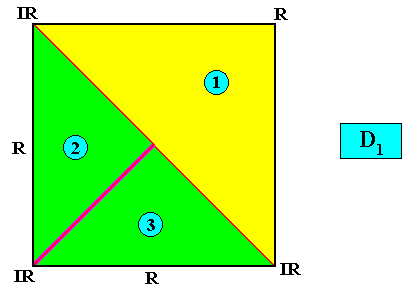
Figure above : A two-dimensional quadratic D1 crystal with three antimers (green, yellow). The three antimers are indicated by numerals.
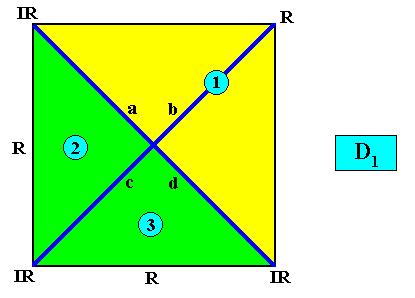
Figure above : Same as previous Figure : a two-dimensional quadratic D1 crystal with three antimers (green, yellow). The Vector Rosette of Actual Growth, with its four vectors a, b, c, d indicated (blue lines).
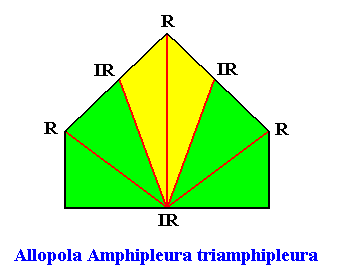
The next Figure gives the promorph (and its name) of the above quadratic crystal ( D1 , three antimers). It is half a 6-fold amphitect polygon, and as such a two-dimensional analogue of half a 6-fold amphitect pyramid (i.e. it is its base).
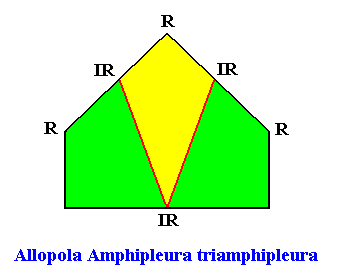
The next Figure is the same, but with the median lines of the antimers omitted, in order to let the latter come out more clearly.
We now consider the second case regarding the position of the mirror line of a two-dimensional quadratic crystal with intrinsic D1 point symmetry : The mirror line (as the only symmetry element of the crystal) is non-diagonal, i.e. it connects the centers of two opposite sides of the square representing our crystal.
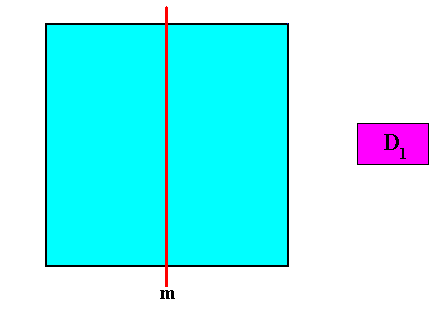
Figure above : The only symmetry element of a two-dimensional D1 quadratic crystal : a mirror line ( m ). The latter is, in the present case, non-diagonal. It connects the centers of two opposite sides of the square.
Three crystallographic Forms are needed to conceptually construct the crystal (i.e. obtaining its four crystal faces that make up a square).
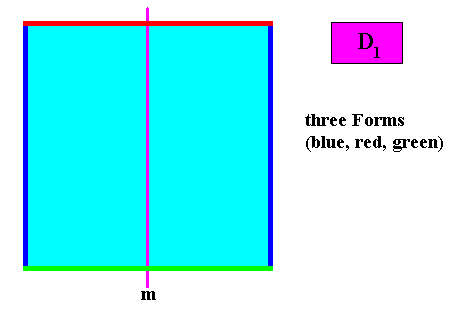
Figure above : Three Forms (blue, red, green) are needed to construct a quadratic D1 two-dimensional crystal, if the mirror line is non-diagonal :
An initial crystal face (blue) implies a second face (blue) in virtue of the mirror line. No further faces will be implied. The result is one Form consisting of two parallel faces (blue). It is an open Form, and cannot therefore represent a crystal. A second initial face (red), perpendicular to the mirror line does not imply new faces. So this is a second Form consisting of one face only (red). These two Forms combined are still an open Form and cannot represent a crystal. A third initial face (green) parallel to the second and (also) perpendicular to the mirror line also does not imply new faces. So it is a Form -- a third Form -- consisting of one face only (green). The three Forms together constitute a closed structure, and the latter is a square and as such represents our crystal.
D1 symmetry and two antimers.
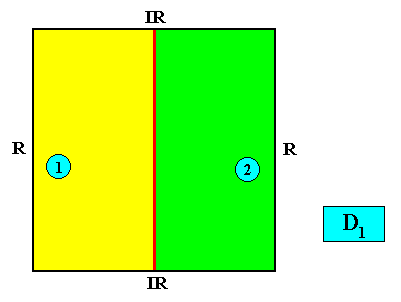
Figure above : A two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing two antimers (green, yellow) indicated by numerals.
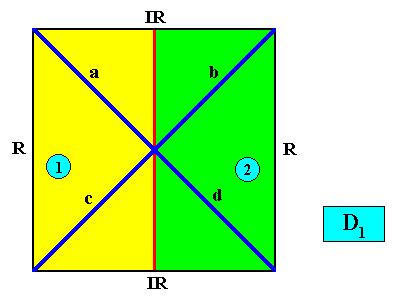
Figure above : Same as previous Figure : a two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing two antimers (green, yellow) indicated by numerals. Included is the crystal's Vector Rosette of Actual Growth, with its four vectors a, b, c, d .
In order to highlight the asymmetry of the antimers, i.e. in order to highlight the absence of a horizontal mirror line in addition to the vertical one, and at the same time to demonstrate the equivalence and non-equivalence of the vectors of the Rosette, we insert a motif (black), first without Vector Rosette :
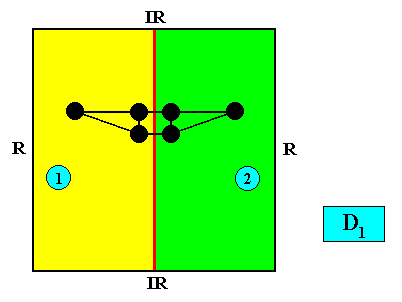
And with the Vector Rosette of Actual Growth added :
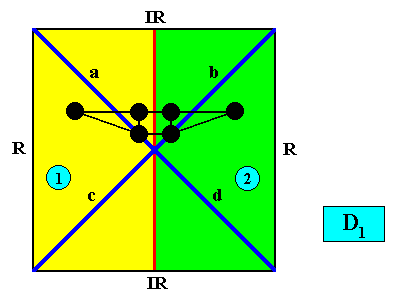
Figure above : Same as earlier Figure (crystal with vector rosette, but without inserted motif) : a two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing two antimers (green, yellow). A motif (black) is inserted. It demonstrates the equivalence of the vectors a and b , and of c and d , and the non-equivalence of a and c , of b and d , of a and d and, finally, of b and c .
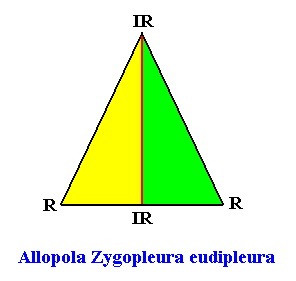
The promorph of such a crystal, i.e. a quadratic D1 crystal with its mirror line non-diagonal and with two antimers, is the same as for the case of a diagonal mirror line. This promorph, i.e. that of the "Allopola Zygopleura eudipleura", was given above .
D1 symmetry and four antimers.
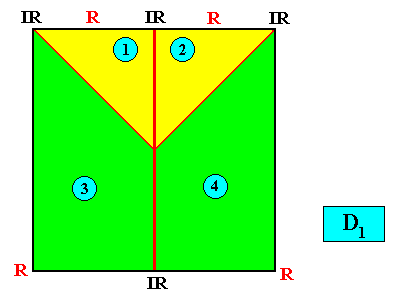
Figure above : A two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing four antimers (green, yellow) indicated by numerals.
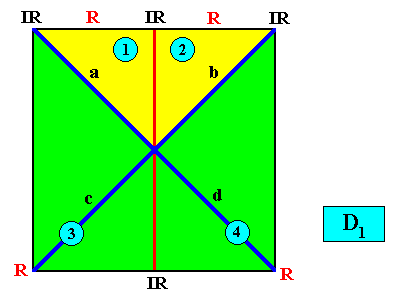
Figure above : Same as previous Figure : a two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing four antimers (green, yellow) indicated by numerals. Included is the crystal's Vector Rosette of Actual Growth, with its four vectors a, b, c, d , where a and b , as well as c and d are equivalent, while a and c , as well as b and d and also a and d as well as b and c are non-equivalent.
The four antimers allow for two types of configuration. One of them is just depicted, the other is depicted in the next Figure :
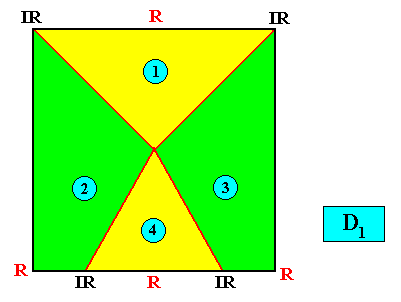
Figure above : A two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing four antimers (green, yellow) indicated by numerals. Alternative configuration of the four antimers.
The promorph of our crystal, i.e. of a quadratic D1 crystal with its mirror line in a non-diagonal position and with four antimers, is the same as for the case where its mirror line is diagonal, viz. either -- dependent on the mentioned configuration of the four antimers -- belonging to the "Allopola Zygopleura Eutetrapleura interradialia" or to the "Allopola Zygopleura Eutetrapleura radialia". They were depicted above .
D1 symmetry and five antimers.
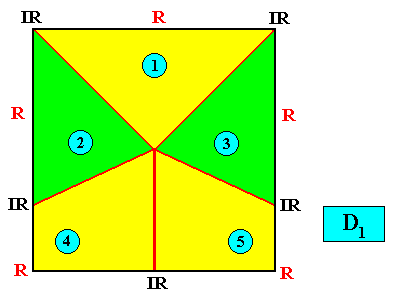
Figure above : A two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing five antimers (green, yellow) indicated by numerals. Only the members of the left-right pairs of vectors of the Vector Rosette of Actual Growth (not drawn) are equivalent.
The next Figures give and name the promorph of our quadratic D1 crystal with five antimers.
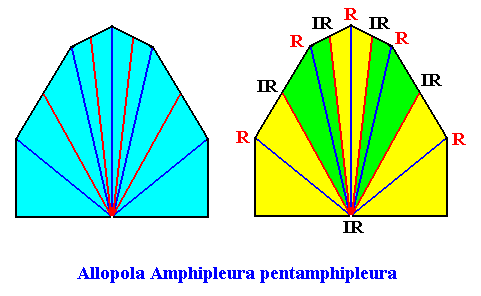
Figure above : Promorph of the two-dimensional quadratic D1 crystal with five antimers. It is half a 10-fold amphitect polygon, and as such a two-dimensional analogue of half a 10-fold amphitect pyramid (i.e. it is its base). In the right image the five antimers (green, yellow) and the radial and interradial directions are indicated.
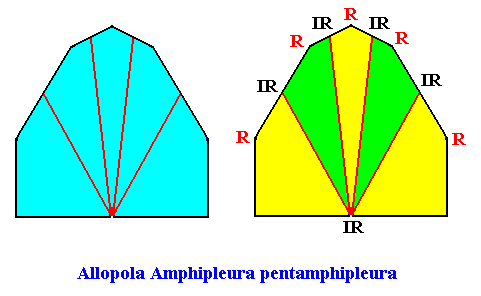
Figure above : Same as previous Figure : promorph of the two-dimensional quadratic D1 crystal with five antimers. Median lines of the antimers omitted in order for the latter to come out more clearly.
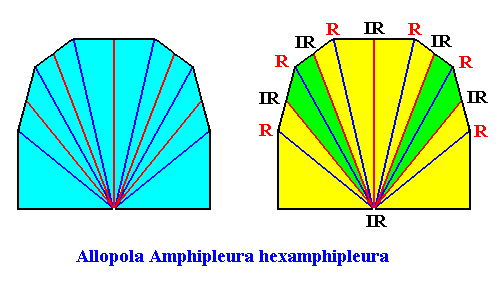
D1 symmetry and six antimers.
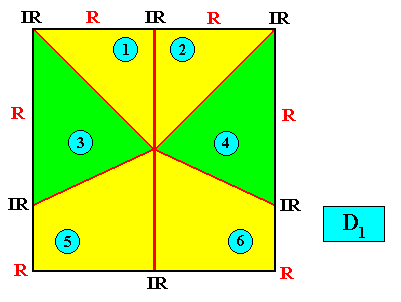
Figure above : A two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing six antimers (green, yellow) indicated by numerals.
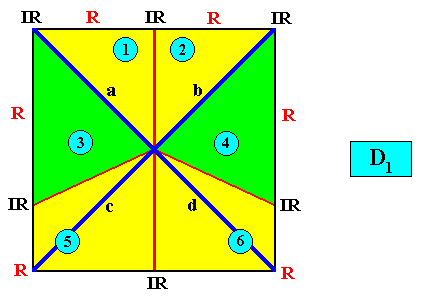
Figure above : Same as previous Figure : a two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing six antimers (green, yellow) indicated by numerals. The Vector Rosette of Actual Growth, with its four vectors a, b, c, d is indicated (blue lines), where a and b , as well as c and d are equivalent, while a and c , as well as b and d and also a and d as well as b and c are non-equivalent.
The promorph of our crystal, i.e. of a quadratic D1 crystal with its mirror line in a non-diagonal position and with six antimers, is the same as for the case where its mirror line is diagonal, viz. belonging to the "Allopola Amphipleura hexamphipleura" . It was depicted above .
D1 symmetry and three antimers.
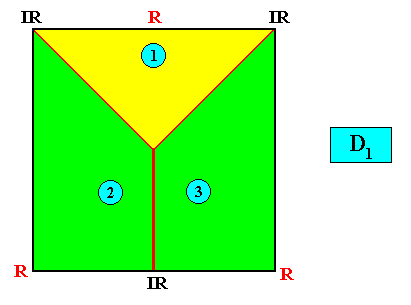
Figure above : A two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing three antimers (green, yellow) indicated by numerals.
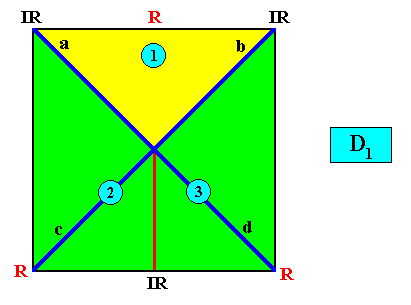
Figure above : Same as previous Figure : a two-dimensional quadratic D1 crystal with its mirror line in a non-diagonal position and possessing three antimers (green, yellow) indicated by numerals. The Vector Rosette of Actual Growth, with its four vectors a, b, c, d is indicated (blue lines), where a and b , as well as c and d are equivalent, while a and c , as well as b and d and also a and d as well as b and c are non-equivalent.
The promorph of our crystal, i.e. of a quadratic D1 crystal with its mirror line in a non-diagonal position and with three antimers, is the same as for the case where its mirror line is diagonal, viz. belonging to the "Allopola Amphipleura triamphipleura" . It was depicted above .
C2 symmetry.
The next Figure indicates the only symmetry element (with respect to point symmetry) of such a crystal.
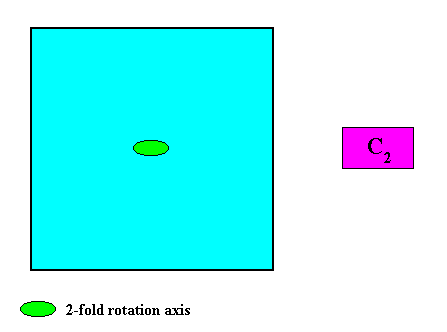
Figure above : A two-dimensional quadratic C2 crystal. Its only symmetry element is a two-fold rotation axis (indicated as a small solid green ellipse) going through the crystal's center (and being, of course, perpendicular to the plane of the drawing).
Two crystallographic Forms are needed to conceptually construct a square crystal having this intrinsic symmetry (C2) :
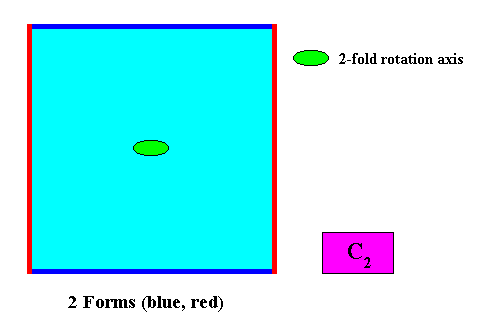
Figure above : A two-dimensional quadratic C2 crystal. Two crystallographic Forms are needed to construct the square : An intial crystal face (blue) implies another face in virtue of the two-fold rotation axis, resulting in a Form consisting of two parallel faces (blue). Another initial face (red), perpendicular to the first one, implies a second face, also resulting in a Form consisting of two parallel faces (red). Combining these two Forms yields the quadratic crystal consisting of four crystal faces.
Quadratic crystals can occur if the (two-fold) motif s.str. plus its corresponding surroundings (together forming the motif s.l.) are stacked according to a quadratic net, which, in the present case, is in fact an oblique net where the angles happen to be 900 and where the two translations happen to be equal in length. See for such a stacking the relevant Figure in Part VII .
C2 symmetry and two antimers.
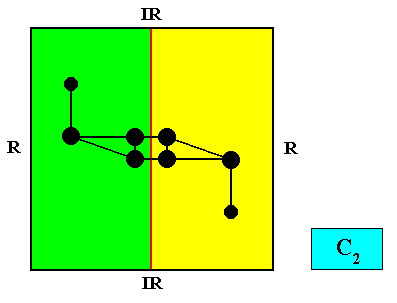
Figure above : A two-dimensional quadratic C2 crystal with two antimers (green, yellow). A motif (black) is inserted in order to indicate the exclusive 2-fold rotational (point) symmetry of the crystal, and therefore the absence of mirror lines. Radial (R) and interradial (IR) directions are indicated.
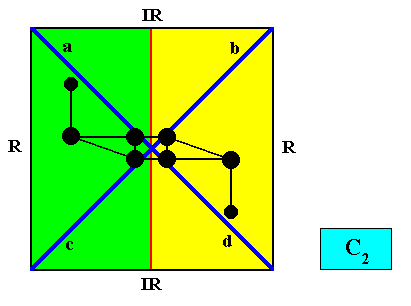
Figure above : Same as previous Figure : a two-dimensional quadratic C2 crystal with two antimers (green, yellow). The Vector Rosette of Actual Growth, with its four vectors a, b, c, d is indicated (blue lines), where a is equivalent to d , and b to c .
The next Figure shows an alternative orientation of the two antimers within the quadratic crystal.
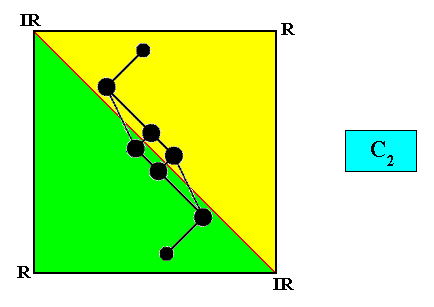
Figure above : Same as previous Figure. Alternative orientation of the two antimers.
It is possible to draw the above quadratic C2 crystal with two antimers without inserting a motif, and nevertheless fully expressing the C2 symmetry and the two antimers, and at the same time expressing the absence of any symmetry elements apart from the 2-fold rotation axis. The next Figure illustrates this.
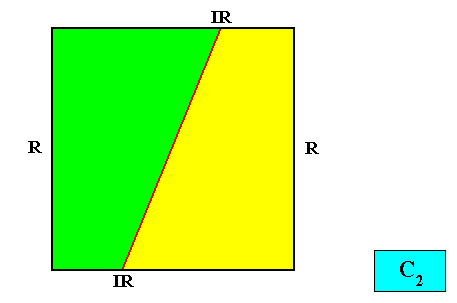
Figure above : A two-dimensional intrinsically quadratic crystal with C2 intrinsic symmetry and two antimers (green, yellow).
The next Figure gives and names the promorph of our quadratic C2 crystal with two antimers.
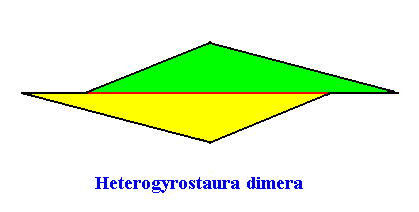
Figure above : Promorph of the quadratic C2 crystal with two antimers. It is a two-fold amphitect gyroid polygon, and as such a two-dimensional analogue of the corresponding three-dimensional two-fold amphitect gyroid pyramid, which is depicted in the next Figure.
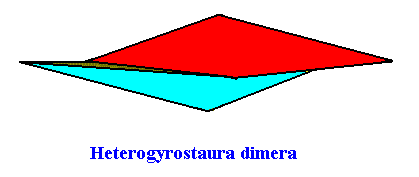
Figure above : Three-dimensional analogue of the promorph of the quadratic two-dimensional C2 crystal with two antimers : slightly oblique top-view of a two-fold amphitect gyroid pyramid.
As has been said, a crystal with C2 point symmetry can have any even number of antimers, depending on the features of its 'chemical' motif. Below we give an example involving eight antimers.
C2 symmetry and eight antimers.
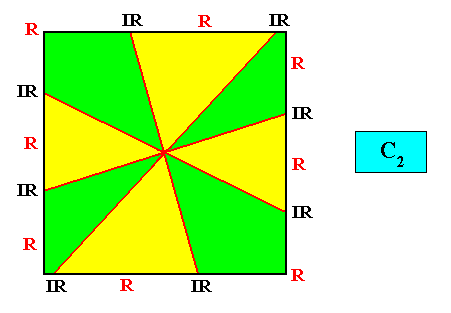
Figure above : A two-dimensional quadratic C2 crystal with eight antimers (green, yellow).
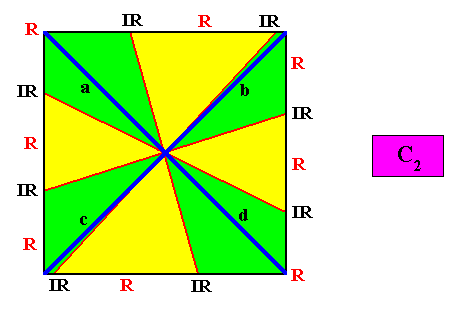
Figure above : Same as previous Figure : a two-dimensional quadratic C2 crystal with eight antimers (green, yellow). The Vector Rosette of Actual Growth, with its four vectors a, b, c, d is indicated (blue lines). Only opposite vectors are equivalent.
The next Figure gives and names the promorph of our two-dimensional quadratic C2 crystal with eight antimers.
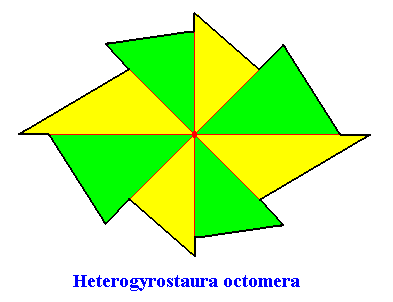
Figure above : Promorph of the above square C2 crystal with eight antimers. It is an 8-fold amphitect gyroid polygon and as such the two-dimensional analogue of an 8-fold amphitect gyroid pyramid (namely its base). The eight antimers (green, yellow) are indicated.
The promorphs of C2 crystals were represented here by polygons (pyramids) with receding angles. They can equally be represented by polygons (pyramids) not involving such angles, as is the case in all single crystals. But because in organisms receding angles are allowed, and because they more clearly indicate the gyroid nature of those promorphs, we prefer such angles to figure in the geometric structures representing such promorphs.
C1 symmetry and no antimers.
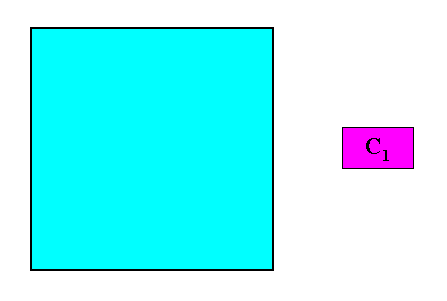
Figure above : Crystals with point symmetry C1 do not have symmetry elements, apart from the trivial 1-fold rotation axis.
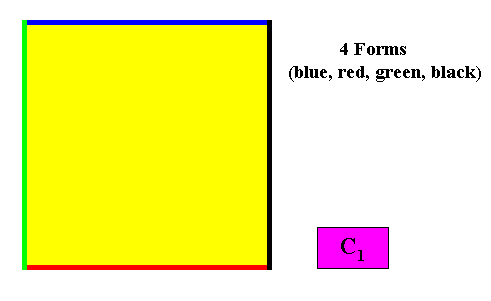
Figure above : For a two-dimensional quadratic C1 crystal to be conceptually constructed, four crystallographic Forms are needed (blue, red, green, black).
In the next Figure an asymmetric motif (black) is added to indicate the asymmetry of the crystal, i.e. to indicate that the crystal's point symmetry is according to the group C1 . The Vector Rosette of Actual Growth, with its four vectors a, b, c, d is indicated (blue lines).
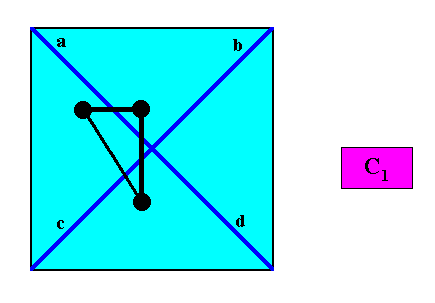
The inserted asymmetric motif (black) clearly shows that the vectors a, b, c, d are all non-equivalent, i.e. each of them is unique, and cannot be transformed in any of the other vectors by whatever symmetry transformation (Recall, that the equivalence or non-equivalence of the vectors takes into account their surroundings). Quadratic crystals can occur if the (asymmetric) motif s.str. plus its corresponding surroundings (together forming the motif s.l.) are stacked according to a quadratic net, which, in the present case, is in fact an oblique net where the angles happen to be 900 and where the translations happen to be equal in length. See for such a stacking the relevant Figure in Part VII .
The next Figure (two images) gives the possible promorphs (and their names) of such a quadratic crystal. The promorph is either (left image) half an isosceles triangle (and, equivalently, a quarter of a rhombus), and is as such the two-dimensional analogue of a quarter of a rhombic pyramid, or (right image) an irregular triangle, indicating two unequal antimers (yellow, green), and is as such the two-dimensional analogue of an irregular pyramid (or, equivalently, a 1-fold pyramid).
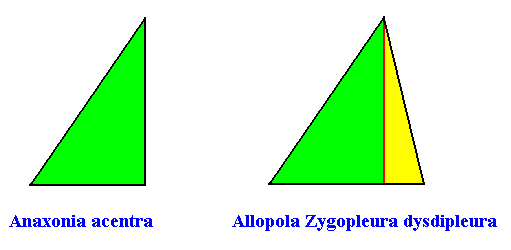
This concludes our investigation concerning the relation of intrinsic quadratic (2-dimensional) crystal shape to intrinsic point symmetry and to promorph.
In the next document we will investigate the third and fourth shapes from our above given list : rectangle, square, parallelogram, rhombus, equilateral triangle, regular hexagon.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part IX.
e-mail : 