General Ontology IX

General Ontology Cosmos and Nomos

Theory of Ontological Layers and Complexity Layers

Part IX

Crystals and Organisms

Theory of intrinsic Shape, intrinsic Symmetry and Promorph

e-mail :

Back to Homepage

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.

Crystals and Organisms, Shape, Symmetry and Promorph.

Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.

Parallelogram / Rhombus

We shall start with the Parallelogram

Let us then consider a fully developed two-dimensional crystal having a parallelogram as its intrinsic shape :

Any parallelogram can be conceived as being built up by a periodic stacking of microscopic parallelogrammatic units, as the next Figure illustrates.

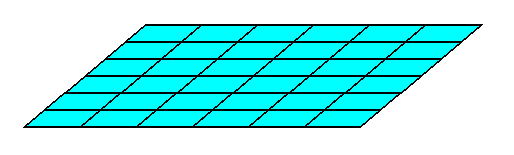
The true (i.e. intrinsic) point symmetry of such a parallelogrammatic crystal is either according to the Cyclic Group C₂ (crystallographically indicated as 2 ), or to the Asymmetric Group C₁ (crystallographically indicated as 1 ), depending on the crystal's internal structure.

That an intrinsically parallelogrammatic crystal can have these intrinsic symmetries can be explained succinctly as follows (and will be further evident in the sequel) :
A Parallelogram as such has the following symmetries, i.e. it will be superposed upon itself by the following transformations (which are for that reason symmetry transformations) :

0⁰ or 360⁰ rotation about any axis.
180⁰ rotation (half-turn) about the axis through its center.

The parallelogrammatic crystal originates by development of crystal faces. These faces will appear in accordance with the available symmetry, i.e. according to the set of symmetry transformations available in each case. And this set is dependent on the symmetry of the motif. An initially given face will imply copies of itself according to this set of available symmetry transformations. The configuration of faces so obtained then constitutes a Form (in the crystallographic sense). So it is clear that :

When no symmetry is available ( a of the above list), four Forms are needed to produce a parallelogram.
When only a half-turn is available ( b of the above list), two Forms are needed to produce a parallelogram.

The next table shows the plane groups that can support (two-dimensional) crystals having the Parallelogram as their intrinsic shape. Further the table shows the intrinsic point symmetry of the crystal (with its crystallographic notation between brackets), and, finally, the number of crystallographic Forms needed to generate such a parallelogrammatic crystal :

Plane Group	Point Symmetry	Number of Forms
P1	C₁ ( 1 )	4
P2	C₂ ( 2 )	2

The Parallelogram is supported by the following plane groups :

P2, which has a point symmetry according to C₂ .
P1, which has a point symmetry according to C₁ .

For each one of these plane groups we will show how it supports a parallelogrammatic crystal shape. The intrinsic shape of the crystal, in the present case its parallelogrammatic shape, depends on the Growth Rate Vector Rosette, which in turn depends on the atomic aspects (chemical nature of motifs and geometry of lattice) presented to the growing environment by the possible crystal faces. The parallelogrammatic crystal can be formed by the stacking of parallelogrammatic building blocks (unit meshes) containing a motif s.str. compatible with the point symmetry implied by the given plane group. The point symmetry is indicated in each case. Recall that the point symmetry of a crystal is the translation-free residue of its plane group symmetry.

A parallelogram, which has a symmetry according to the group C₂ , will be supported by those plane groups of which all the implied point symmetries (i.e. implied by the plane group) are also symmetries of the Parallelogram. This does not necessarily hold the other way around : A crystal can have an intrinsic shape that is a parallelogram, but nevertheless some, or even all, symmetries of this parallelogram can be absent in the crystal, resulting in the fact that the intrinsic symmetry of the crystal is lower than that of its intrinsic shape.

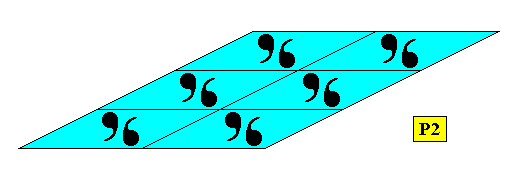
Figure above : A parallelogrammatic two-dimensional C₂ crystal supported by an oblique point lattice (indicated by connection lines).

Figure above : A parallelogrammatic two-dimensional C₁ crystal supported by an oblique point lattice (indicated by connection lines).

This concludes a summary, showing when, and in what way, parallelogrammatic two-dimensional crystals are supported. As can be seen in the above Figures the actual point symmetry of the (parallelogrammatic) crystal can be lower than that of the Parallelogram. So in the Figure just above, we see a crystal having the (intrinsic) shape of a parallelogram, which as such has C₂ symmetry, wheras the crystal itself has a point symmetry according to the group C₁ , because its parallelogrammatic meshes are provided with an asymmetric motif, destroying the crystal's symmetry, i.e. lowering its symmetry from C₂ to C₁ .
In the next document we will investigate the promorphs of these parallelogrammatic two-dimensional crystals, while in the present document we will consider intrinsically rhombus-shaped crystals (as a prelude to the study of their promorphs).

Now we shall deal with the

Rhombus

So let us consider a fully developed two-dimensional crystal having a rhombus as its intrinsic shape (a rhombus is a parallelogram with all sides of equal length) :

Any rhombus-shaped crystal can be conceived as being built up by a periodic stacking of microscopic rhombus-shaped units, as the next Figure illustrates.

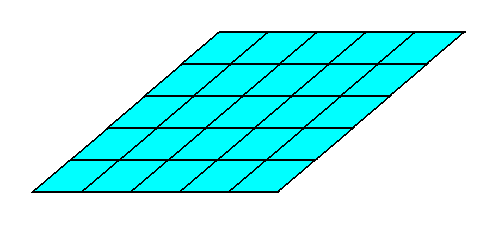
The true point symmetry of such an intrinsically rhombic crystal is either according to the Dihedral Group D₂ (crystallographically denoted by 2mm ), or to the Dihedral Group D₁ (crystallographically denoted by m ), or to the Cyclic Group C₂ (crystallographically denoted by 2 ), or, finally, to the Asymmetric Group C₁ , all depending on the crystal's internal structure.

That a rhombic crystal (i.e. a two-dimensional crystal having as its intrinsic shape the rhombus) can possess either of these symmetries can be explained succinctly as follows (and will be further evident in the sequel) :
A Rhombus as such has the following symmetries, i.e. it will be superposed upon itself by the following transformations (which are then for that reason symmetry transformations) :

0⁰ or 360⁰ rotation about any axis.
180⁰ rotation (half-turn) about the axis through its center.
Reflection in a line connecting two opposite corners.
Reflection in a line connecting two opposite corners and perpendicular to the one just mentioned (c).

The rhombus-shaped crystal originates by development of crystal faces. These faces will appear in accordance with the available symmmetry, i.e. according to the set of symmetry transformations available in each case. And this set is dependent on the symmetry of the motif. An initially given face will imply copies of itself according to this set of available symmetry transformations. The configuration of faces so obtained then constitutes a Form (in the crystallographic sense). So it is clear that :

When no symmetry is available ( a of the above list), four Forms are needed to produce a rhombus.
When only a half-turn is available ( b of the above list), two Forms are needed to produce a rhombus.
When only one reflection is available ( c or d of the above list), two Forms are needed to produce a rhombus.
When two reflections are available ( c and d of the above list), only one Form is needed to produce a rhombus.

The next table shows which plane groups can support rhombus-shaped (two-dimensional) crystals. It further indicates the corresponding point groups (with the crystallographic notation in brackets), and finally the number of crystallographic Forms needed in each case (i.e. each case of different point symmetry) to produce a rhombus :

Plane Group	Point Symmetry	Number of Forms
P1	C₁ ( 1 )	4
P2	C₂ ( 2 )	2
Pm Cm Pg	D₁ ( m )	2
P2mm C2mm P2mg P2gg	D₂ ( 2mm )	1

So the Rhombus is supported by the following plane groups :

P2mm, C2mm, P2mg, P2gg, which have a point symmetry according to D₂ .
Pm, Cm, Pg, which have a point symmetry according to D₁ .
P2, which has a point symmetry according to C₂ .
P1, which has a point symmetry according to C₁ (asymmetric group).

For each of these plane groups we will show how it supports a rhombic crystal shape. The intrinsic shape of the crystal, in the present case its rhombic shape, depends on the Growth Rate Vector Rosette, which in turn depends on the atomic aspects (chemical nature of motifs and geometry of lattice) presented to the growing environment by the possible crystal faces. The rhombic crystal can be formed by the stacking of rectangular or rhombic building blocks (unit meshes) containing a motif s.str. compatible with the point symmetry implied by the given plane group. The point symmetry is indicated in each case. Recall that the point symmetry of a crystal is the translation-free residue of its plane group symmetry.

A rhombus, which has a symmetry according to the group D₂ , will be supported by those plane groups of which all the implied point symmetries (i.e. implied by the plane group) are also symmetries of the Rhombus. This does not necessarily hold the other way around : A crystal can have an intrinsic shape that is a rhombus, but nevertheless some, or even all, symmetries of this rhombus can be absent in the crystal, resulting in the fact that the intrinsic symmetry of the crystal is lower than that of its intrinsic shape.

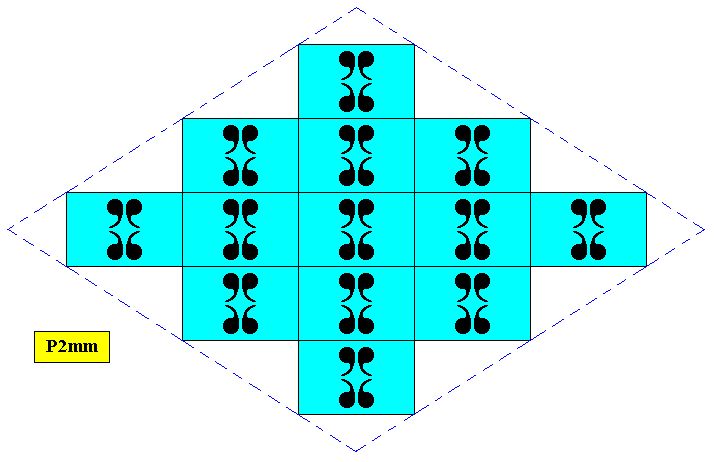
Figure above : A rhombus-shaped two-dimensional D₂ crystal supported by a primitive rectangular point lattice (indicated by connection lines).

In order to have a better overview of such a crystal, we depict a somewhat different and smaller version of it :

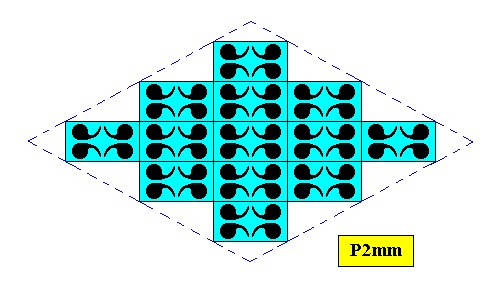
Figure above : A rhombus-shaped two-dimensional D₂ crystal supported by a primitive rectangular point lattice (indicated by connection lines).

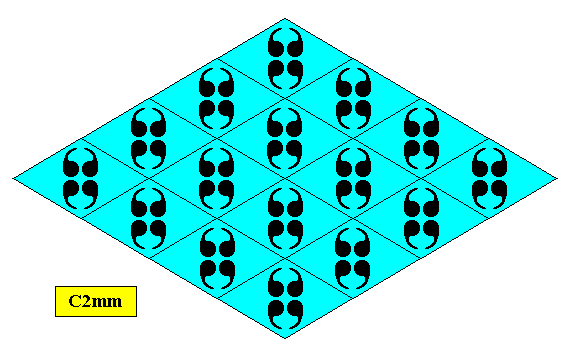
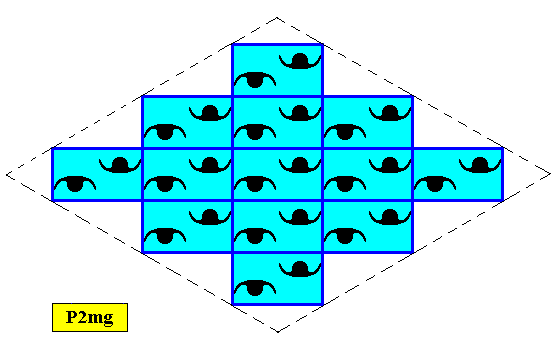
Figure above : A rhombus-shaped two-dimensional D₂ crystal supported by a rhombic point lattice (indicated by connection lines).

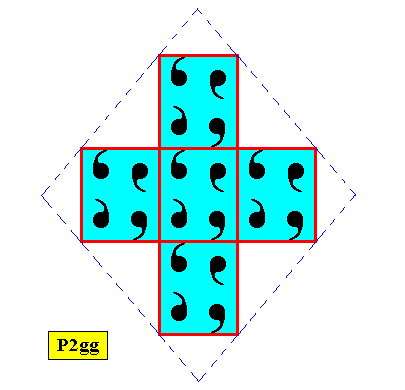
Figure above : A rhombus-shaped two-dimensional D₂ crystal supported by a primitive rectangular point lattice (indicated by connection lines).

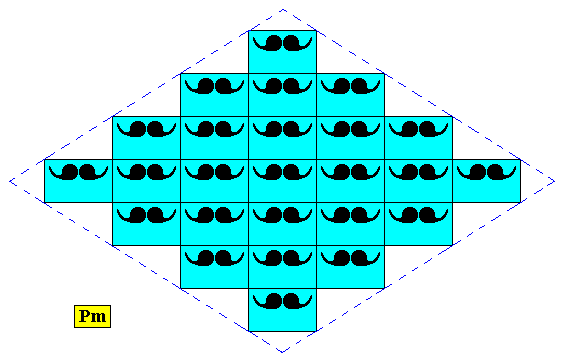
Figure above : A rhombus-shaped two-dimensional D₁ crystal supported by a primitive rectangular point lattice (indicated by connection lines).

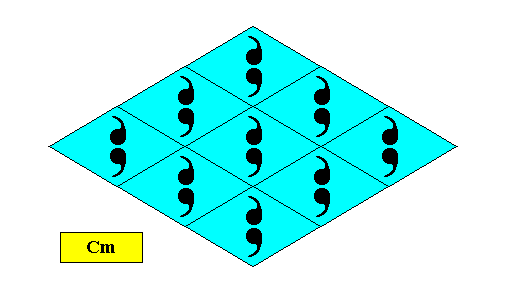
Figure above : A rhombus-shaped two-dimensional D₁ crystal supported by a rhombic point lattice (indicated by connection lines).

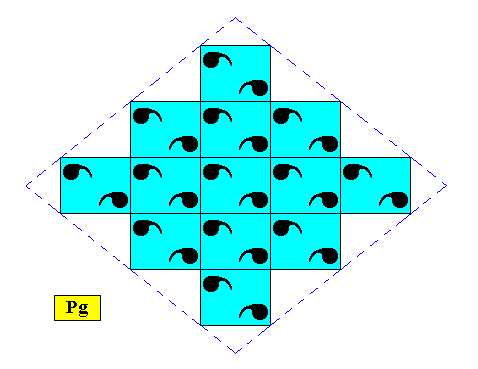
Figure above : A rhombus-shaped two-dimensional D₁ crystal supported by a primitive rectangular point lattice (indicated by connection lines).

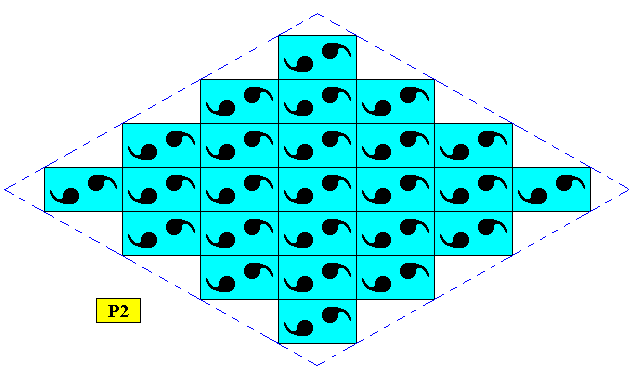
Figure above : A rhombus-shaped two-dimensional C₂ crystal supported by an oblique point lattice (indicated by connection lines) where the angles happen to be 90⁰.

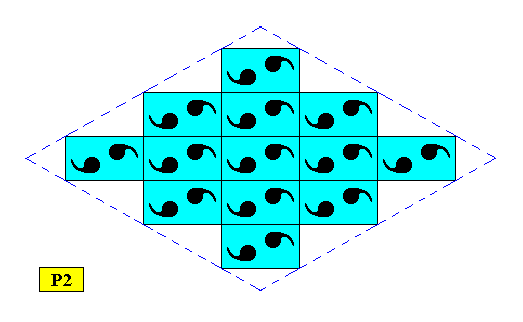
Figure above : Same as previous Figure, but smaller version : A rhombus-shaped two-dimensional C₂ crystal supported by an oblique point lattice (indicated by connection lines) where the angles happen to be 90⁰.

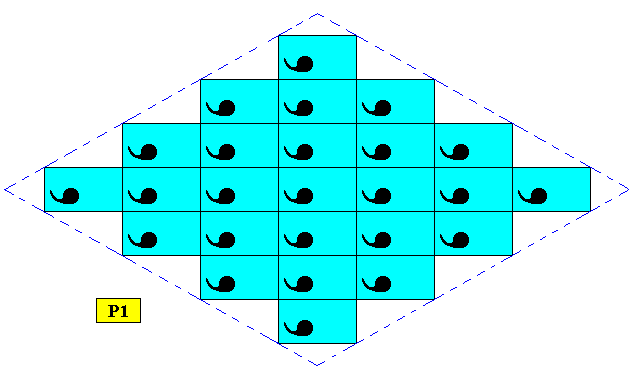
Figure above : A rhombus-shaped two-dimensional C₁ crystal supported by an oblique point lattice (indicated by connection lines) where the angles happen to be 90⁰.

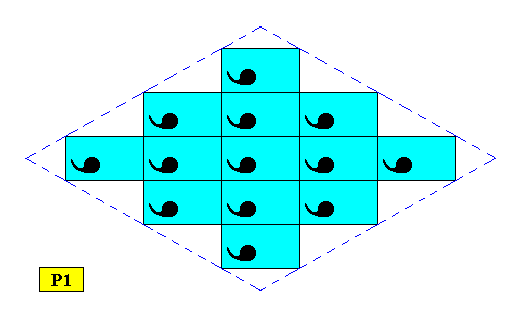
Figure above : Same as previous Figure, but smaller version : A rhombus-shaped two-dimensional C₁ crystal supported by an oblique point lattice (indicated by connection lines) where the angles happen to be 90⁰.

This concludes a summary, showing when, and in what way, rhombus-shaped two-dimensional crystals are supported. As can be seen in the above Figures, in many cases the actual point symmetry of the (rhombus-shaped) crystal is lower than that of the Rhombus.

In the next document we will investigate the promorphs of such crystals.

e-mail :

To continue click HERE for further study of the Theory of Layers, Part X.

e-mail :