(takes a little while to load the images)
General Ontology
Cosmos and Nomos
Theory of Ontological Layers and Complexity Layers

Part XXIX

Crystals and Organisms

Theory of intrinsic Shape, intrinsic Symmetry and Promorph
e-mail : 

Back to Homepage
This document continues the investigation of special categories (If / Then  constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.

Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Summary and evaluation (of the Parts XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).

In the present document we will summarize and evaluate the results of the discussions concerning two-dimensional crystals with more complex intrinsic shapes, as we had them in the foregoing documents. These more complex (intrinsic) shapes were :

First we summarize the results of Part XVI --- XXVII from the viewpoint of intrinsic shape of holomorphic two-dimensional crystals. For each such shape we gave some examples of possible promorphs :

Amphitect Gyroid Hexagon :
Amphitect Gyroid Octagon :
Amphitect Hexagon :
Amphitect Octagon :
Bilateral Hexagon :
Bilateral Octagon :
Bilateral Tetragon :
Bilateral Trigon :
Bilateral Pentagon :
Regular Gyroid Ditetragon :
Regular Ditetragon :
Regular Gyroid Ditrigon :
Regular Gyroid Dihexagon :

We will now summarize these same results, but this time from the viewpoint of promorph.
Only holomorphic crystals are listed. Recall that a holomorphic crystal has its intrinsic symmetry the same as the symmetry of its intrinsic shape. Holomorphic crystals can come in two different varieties, viz. eupromorphic or non-eupromorphic. An eupromorphic crystal is such that its promorph is directly evident from its intrinsic shape.
Promorphs are geometric figures. And, in particular, two-dimensional promorphs are polygons.  Of the latter, first the more general promorphological category will be given in our listing below, i.e. we first give the (more) general category of polygons to which the given particular promorph belongs, say Heterostaura autopola, which are amphitect polygons (i.e. flattened polygons with two mirror lines perpendicular to each other).  Then, if necessary, a lower, but still general subcategory is given, say, Autopola oxystaura (amphitect polygons with 6, 8, 10, .  .  . , antimers).  Finally, the ultimate promorph is given, say, Autopola Oxystaura octophragma, which are amphitect polygons with eight antimers. The planimetric figure representing this promorph is then given.
After this, one or more examples of two-dimensional holomorphic crystals are given that possess this promorph. It is then stated whether this crystal is eupromorphic or non-eupromorphic, and finally that crystal's intrinsic shape is indicated.
Summary of the Promorphs of some two-dimensional Holomorphic crystals
(First) General promorphological category :  Homostaura (regular polygons) :
Homostaura Isopola tetractinota

(Regular polygons with equipolar cross axes and four antimers)
Planimetric Basic Form, representing this promorph :
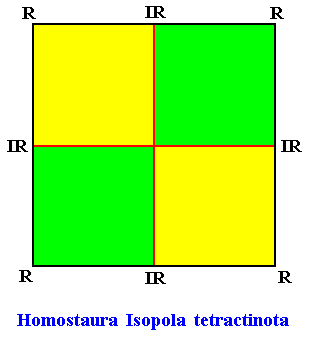
Example of holomorphic crystal :

Non-eupromorphic crystal.
Intrinsic shape : Regular Ditetragon
General promorphological category :  Dihomostaura (regular bipolygons) :
Dihomostaura Isopola tetractinota

(Regular bipolygons with equipolar cross axes and eight similar antimers, four by four equal, and each mirror symmetric)
Planimetric Basic Form, representing this promorph :
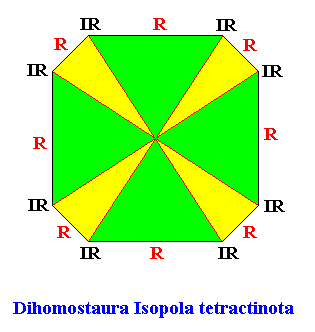
Example of holomorphic crystal :

Eupromorphic crystal
Intrinsic shape : Regular Ditetragon
General promorphological category :  Heterostaura Autopola (amphitect polygons),
Autopola oxystaura (autopola with 6, 8, 10, ..., antimers, therefore at least three radial cross axes present, that must, consequently intersect at  a c u t e  angles) :
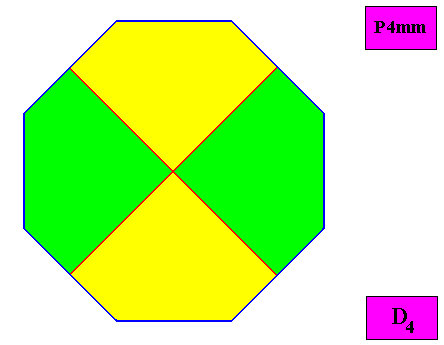
Autopola Oxystaura octophragma

(amphitect polygons with eight antimers)
Planimetric Basic Form, representing this promorph :
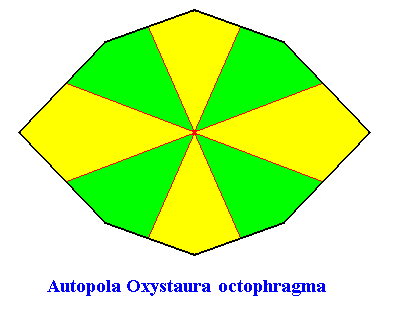
Example of holomorphic crystal :

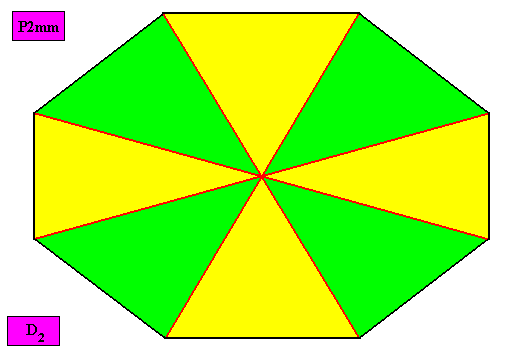Eupromorphic crystal
Intrinsic shape : Amphitect Octagon
Autopola Oxystaura hexaphragma

(amphitect polygons with six antimers)
Planimetric Basic Form, representing this promorph :
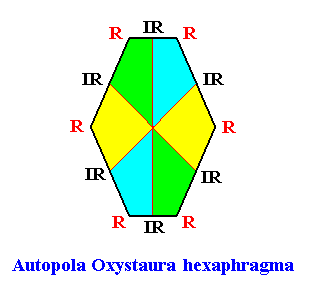
Example of holomorphic crystal :

Eupromorphic crystal
Intrinsic shape : Amphitect Hexagon
General promorphological category :  Heterostaura Autopola (amphitect polygons),
Autopola orthostaura (autopola with 4 or 2 antimers, i.e. tetraphragma or diphragma :  therefore there is either only one radial cross axis present, or two radial cross axes, coinciding with respectively with one or two directional axes. In the latter case these radial cross axes are  p e r p e n d i c u l a r  to each other, i.e. they intersect at right angles),
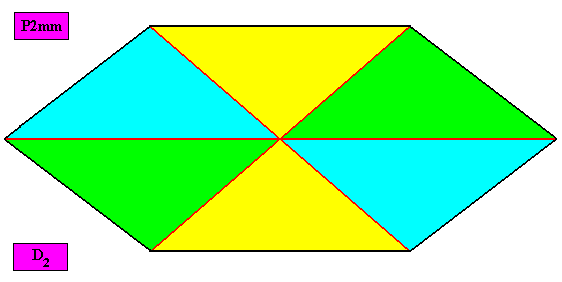
Orthostaura tetraphragma (orthostaura with four antimers) :
Autopola Orthostaura Tetraphragma radialia

(amphitect polygons, here rhombi, with four antimers and with radial directional axes)
Planimetric Basic Form, representing this promorph :
Examples of holomorphic crystals :

Non-eupromorphic crystal
Intrinsic shape : Amphitect Hexagon
-----------------------------------------------
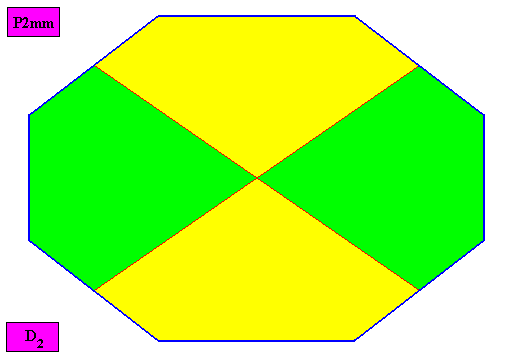Non-eupromorphic crystal
Intrinsic shape : Amphitect Octagon
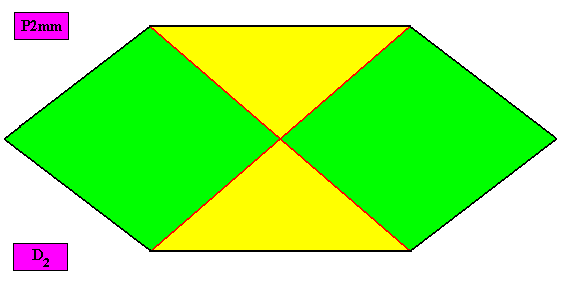
Autopola Orthostaura Tetraphragma interradialia

(amphitect polygons, here rectangles or rhombi, with four antimers and with interradial directional axes)
Planimetric Basic Form, representing this promorph :
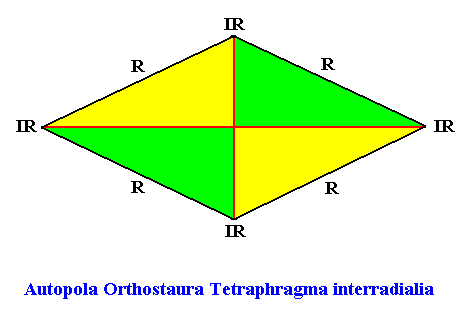
Examples of holomorphic crystals :

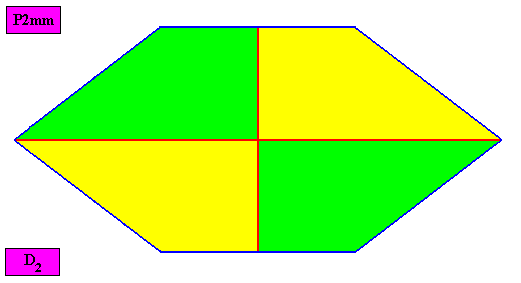Non-eupromorphic crystal
Intrinsic shape : Amphitect Hexagon
---------------------------------------------
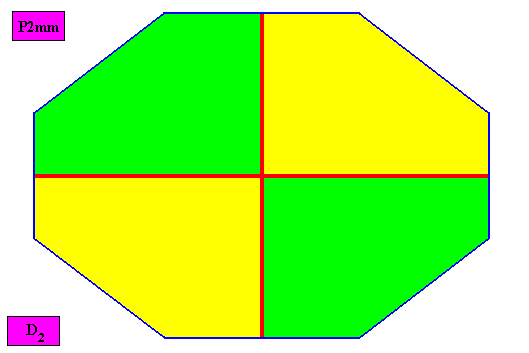Non-eupromorphic crystal
Intrinsic shape : Amphitect Octagon
Autopola Orthostaura Diphragma

(amphitect polygons, here rhombi, with two antimers)
Planimetric Basic Form, representing this promorph :
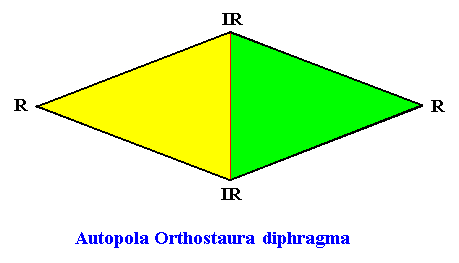
Examples of holomorphic crystals :

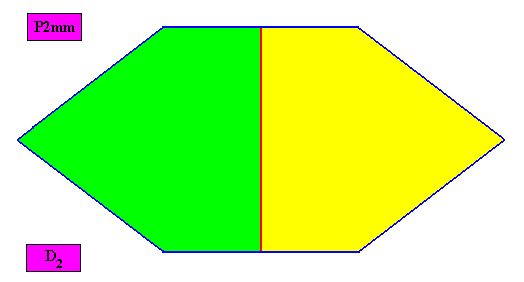Non-eupromorphic crystal
Intrinsic shape : Amphitect Hexagon
-----------------------------------------------
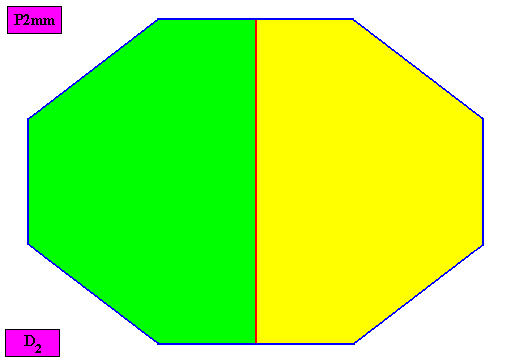Non-eupromorphic crystal
Intrinsic shape : Amphitect Octagon

General promorphological category :  Gyrostaura (gyroid, i.e. twisted, polygons) homogyrostaura (regular gyroid polygons) :
Homogyrostaura hexamera

(Regular gyroid polygons with six antimers)
Planimetric Basic Form, representing this promorph :
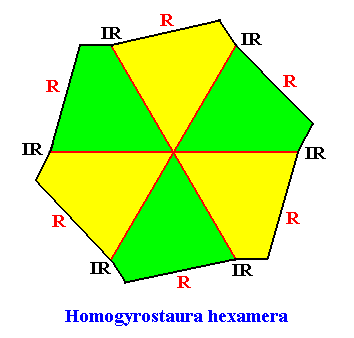
Example of holomorphic crystal :

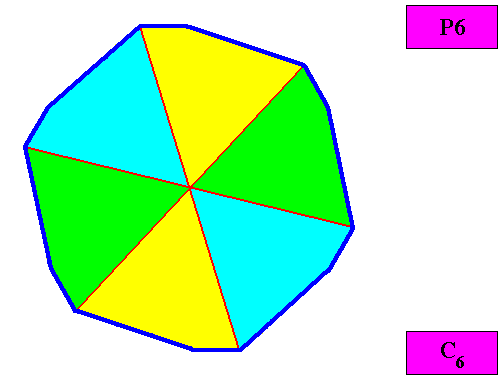Non-eupromorphic crystal
Intrinsic shape :  Regular Gyroid Dihexagon
Homogyrostaura dihexamera

(Regular gyroid polygons with 12 similar, six by six equal antimers)
Planimetric Basic Form, representing this promorph :
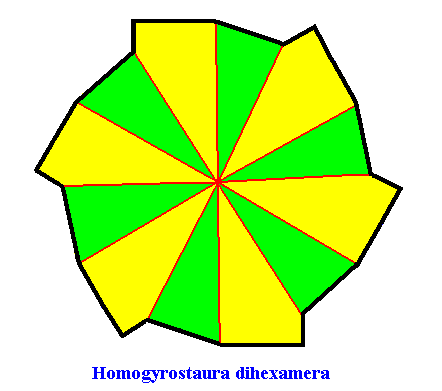
Example of holomorphic crystal :

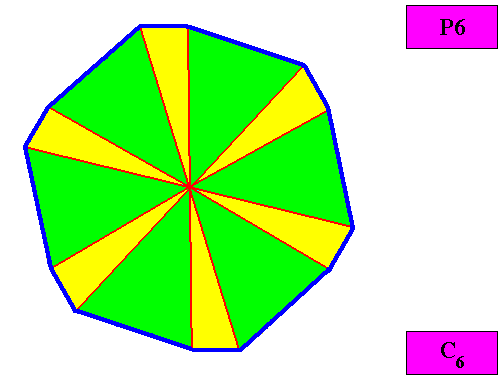Eupromorphic crystal
Intrinsic shape :  Regular Gyroid Dihexagon
Homogyrostaura tetramera

(Regular gyroid polygons with four antimers)
Planimetric Basic Form, representing this promorph :
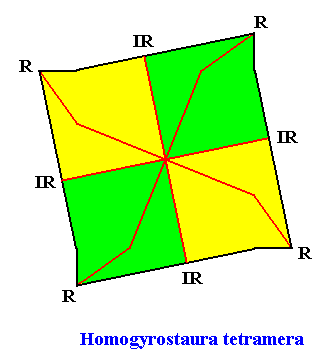
The next two Figures illustrate this basic form still further by giving equivalent geometric figures all representing and expressing the same promorph :
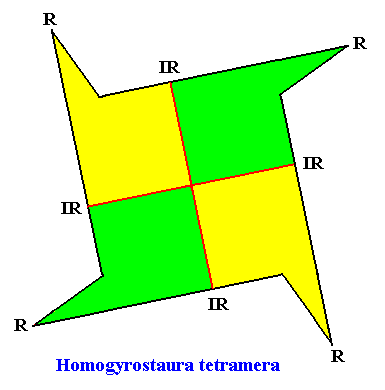
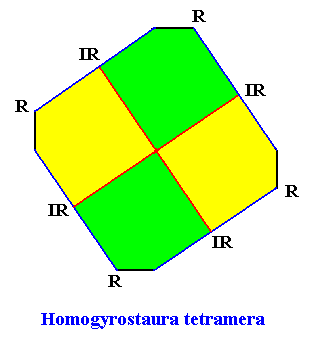
Example of holomorphic crystal :

Non-eupromorphic crystal
Intrinsic shape :  Regular Gyroid Ditetragon
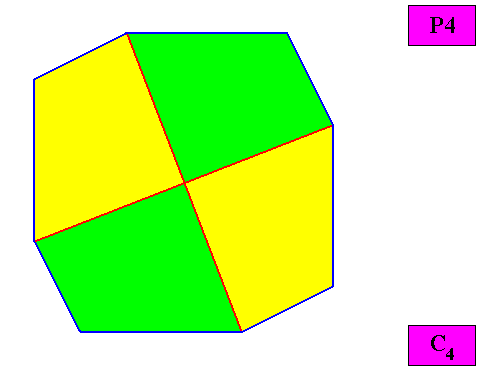
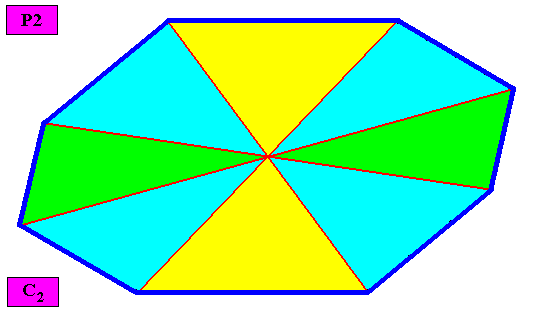
Homogyrostaura ditetramera

(Regular gyroid polygons with eight similar, four by four equal antimers)
Planimetric Basic Form, representing this promorph :
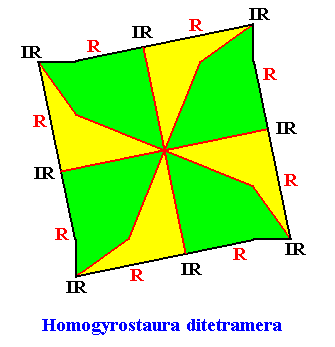
Example of holomorphic crystal :

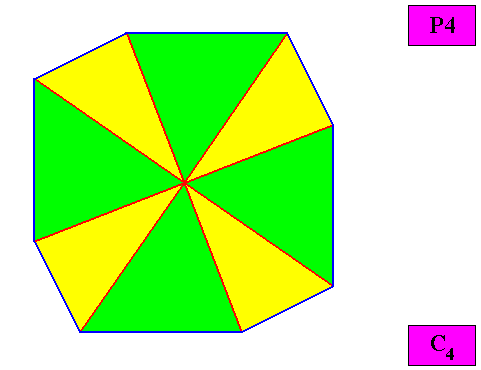Eupromorphic crystal
Intrinsic shape :  Regular Gyroid Ditetragon
Homogyrostaura trimera

(Regular gyroid polygons with three antimers)
Planimetric Basic Form, representing this promorph :
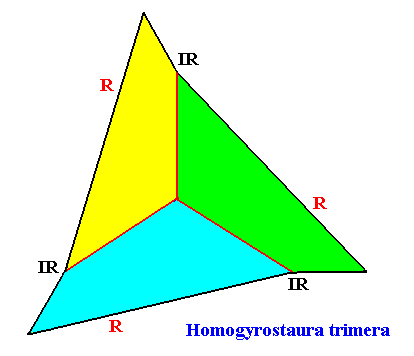
Example of holomorphic crystal :

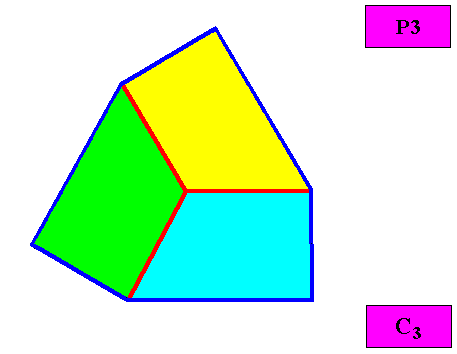Non-eupromorphic crystal
Intrinsic shape :  Regular Gyroid Ditrigon
Homogyrostaura ditrimera

(Regular gyroid polygons with six similar and three by three equal antimers)
Planimetric Basic Form, representing this promorph :
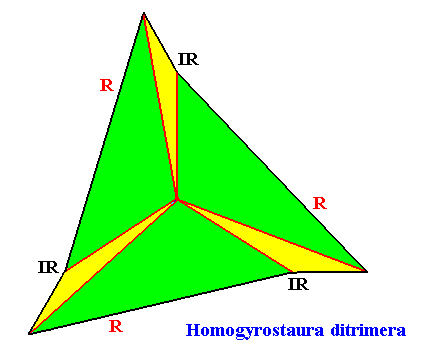
Example of holomorphic crystal :

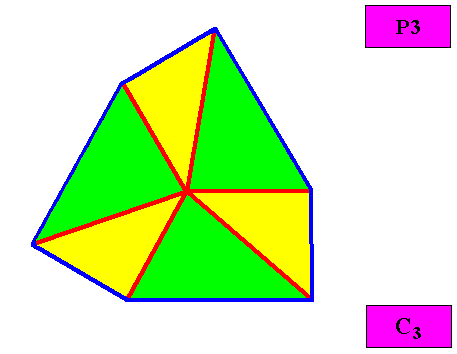Eupromorphic crystal
Intrinsic shape :  Regular Gyroid Ditrigon
Gyrostaura (gyroid, i.e. twisted, polygons) heterogyrostaura (amphitect, i.e. flattened, gyroid polygons) :
Heterogyrostaura octomera

(amphitect gyroid polygons with eight antimers)
Planimetric Basic Form, representing this promorph :
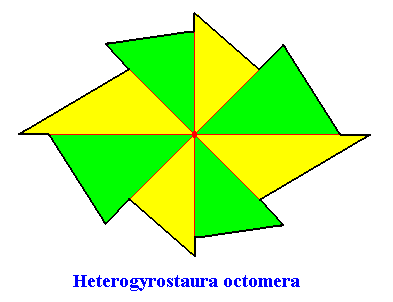
Example of holomorphic crystal :

Eupromorphic crystal
Intrinsic shape :  Amphitect Gyroid Octagon
Heterogyrostaura hexamera

(amphitect gyroid polygons with six antimers)
Planimetric Basic Form, representing this promorph :
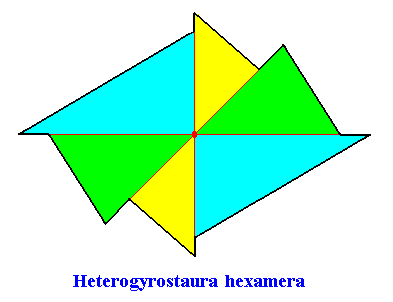
Examples of holomorphic crystals :

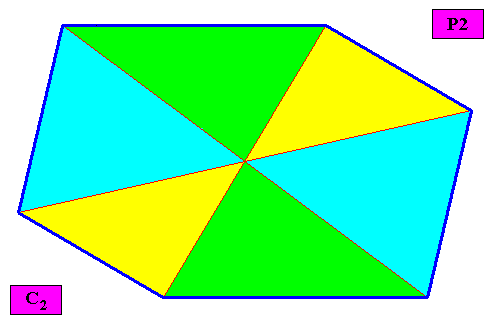Eupromorphic crystal
Intrinsic shape :  Amphitect Gyroid Hexagon
--------------------------------------------
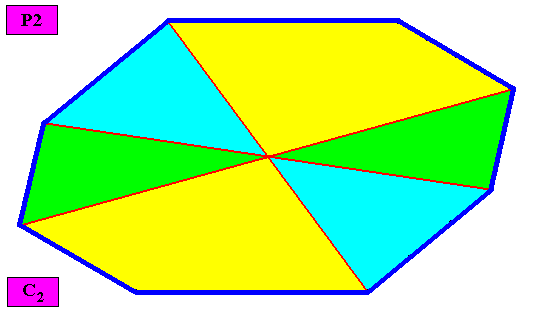Non-eupromorphic crystal
Intrinsic shape :  Amphitect Gyroid Octagon
Heterogyrostaura tetramera

(amphitect gyroid polygons with four antimers)
Planimetric Basic Form, representing this promorph :
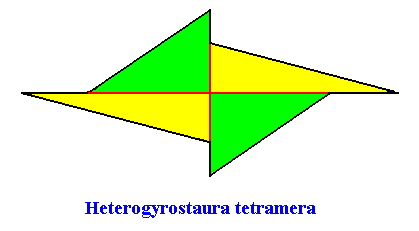
Examples of holomorphic crystals :

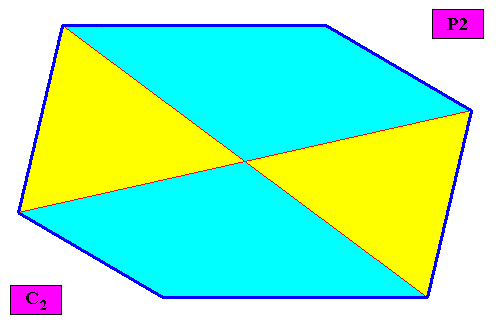Non-eupromorphic crystal
Intrinsic shape :  Amphitect Gyroid Hexagon
-----------------------------------------
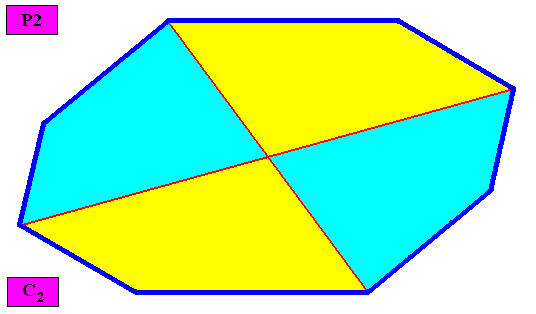Non-eupromorphic crystal
Intrinsic shape :  Amphitect Gyroid Octagon
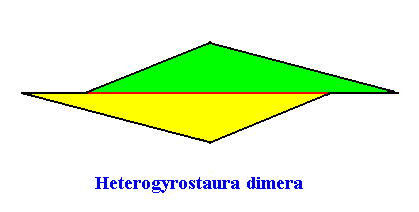
Heterogyrostaura dimera

(amphitect gyroid polygons with two antimers)
Planimetric Basic Form, representing this promorph :
Examples of holomorphic crystals :

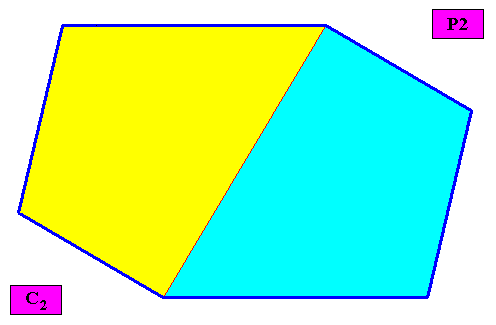Non-eupromorphic crystal
Intrinsic shape :  Amphitect Gyroid Hexagon
-------------------------------------------------
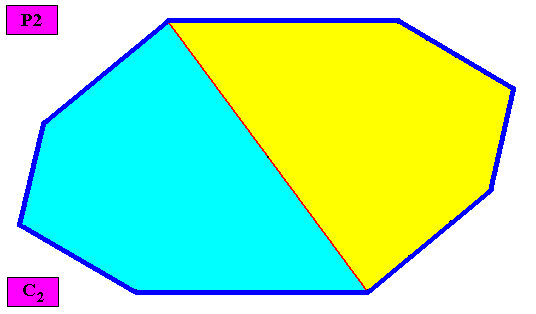Non-eupromorphic crystal
Intrinsic shape :  Amphitect Gyroid Octagon
Heterostaura Allopola (half amphitect polygons, bilateral forms),
Allopola amphipleura (bilateral forms with 3, 5, 6, 7, 8, ... antimers) :
Allopola octamphipleura

(half amphitect polygons, with eight antimers)
Planimetric Basic Form, representing this promorph :
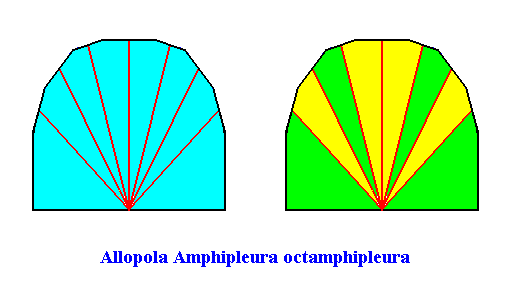
Example of holomorphic crystal :

Eupromorphic crystal
Intrinsic shape :  Bilateral Octagon
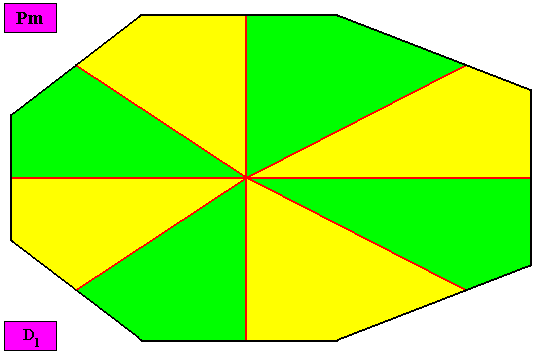
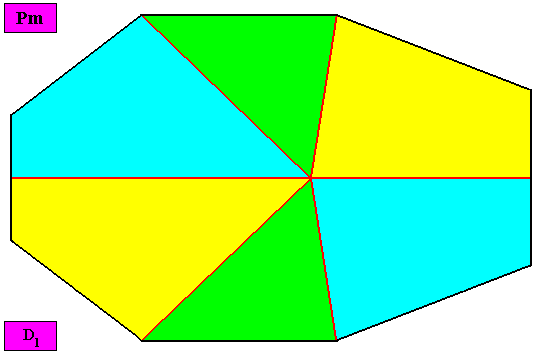
Allopola hexamphipleura

(half amphitect polygons, with six antimers)
Planimetric Basic Form, representing this promorph :
Examples of holomorphic crystals :

Non-eupromorphic crystal
Intrinsic shape :  Bilateral Octagon
---------------------------------------------
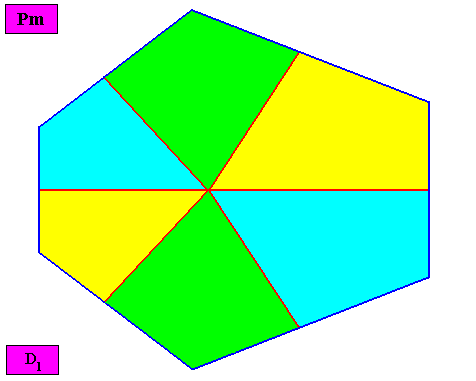Eupromorphic crystal
Intrinsic shape :  Bilateral Hexagon
---------------------------------------------
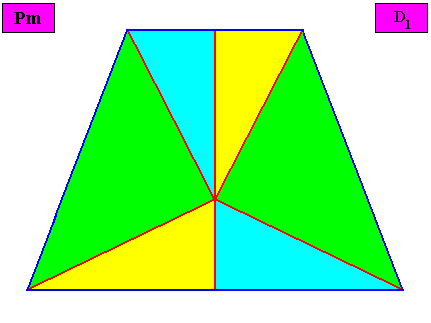Non-eupromorphic crystal
Intrinsic shape Bilateral Tetragon
------------------------------------------------
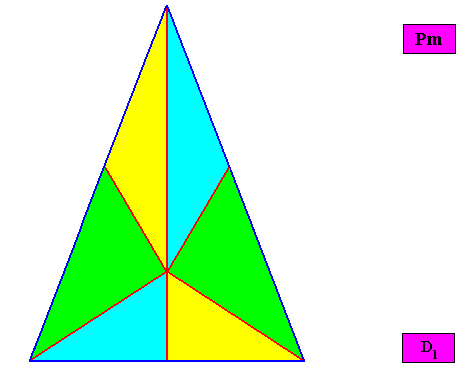Non-eupromorphic crystal
Intrinsic shape :  Bilateral Trigon
Allopola pentamphipleura

(half amphitect polygons, with five antimers)
Planimetric Basic Form, representing this promorph :
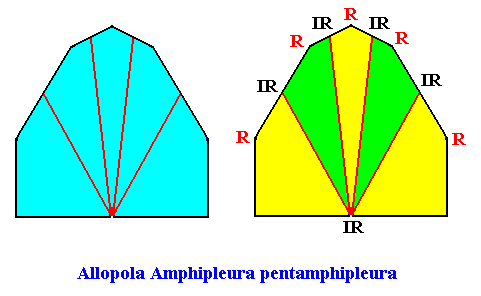
Examples of holomorphic crystals :

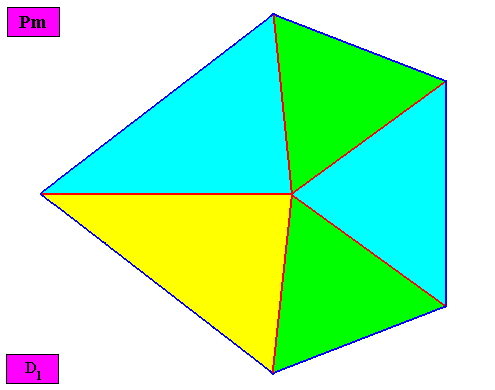Eupromorphic crystal
Intrinsic shape :  Bilateral Pentagon
----------------------------------------------

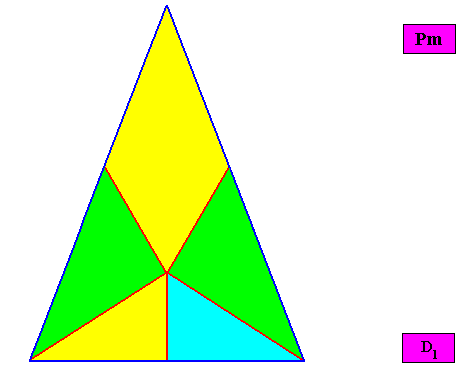
Non-eupromorphic crystal
Intrinsic shape :  Bilateral Trigon
Allopola triamphipleura

(half amphitect polygons, with three antimers)
Planimetric Basic Form, representing this promorph :
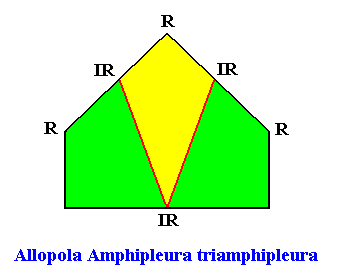
Examples of holomorphic crystals :

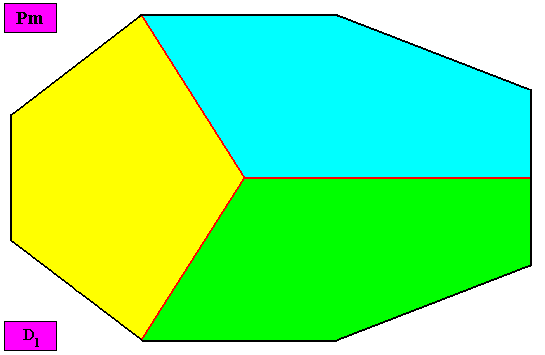Non-eupromorphic crystal
Intrinsic shape :  Bilateral Octagon
--------------------------------------------------
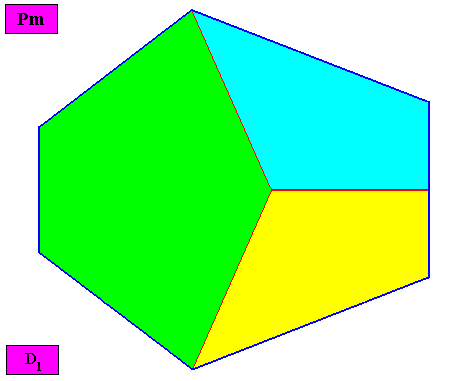Non-eupromorphic crystal
Intrinsic shape :  Bilateral Hexagon
------------------------------------------------
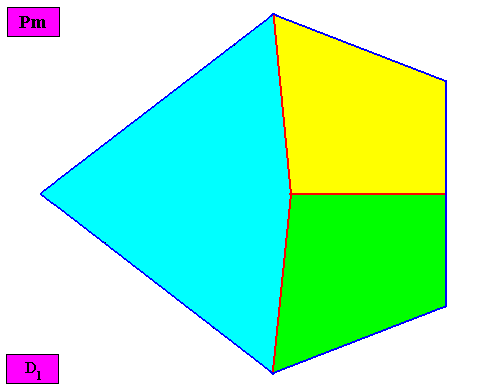Non-eupromorphic crystal
Intrinsic shape :  Bilateral Pentagon
----------------------------------------------
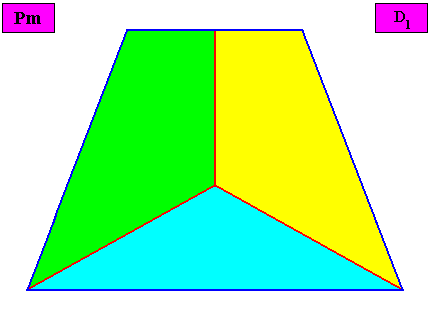Non-eupromorphic crystal
Intrinsic shape :  Bilateral Tetragon
------------------------------------------------

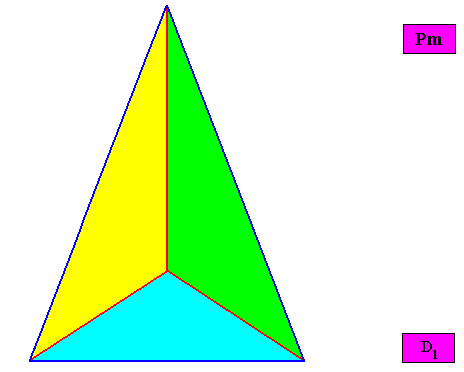
Eupromorphic crystal
Intrinsic shape :  Bilateral Trigon
Heterostaura Allopola (half amphitect polygons,  bilateral forms),
Allopola zygopleura (half rhombic polygons [i.e. isosceles triangles], or isosceles trapezia [i.e. bilateral tetragons] ;  bilateral forms with four or two antimers),

Zygopleura Eutetrapleura (symmetric zygopleura with four antimers) :
Eutetrapleura radialia

(zygopleura with four antimers and radial directional axes,  bi-isosceles triangles)
Planimetric Basic Form, representing this promorph :
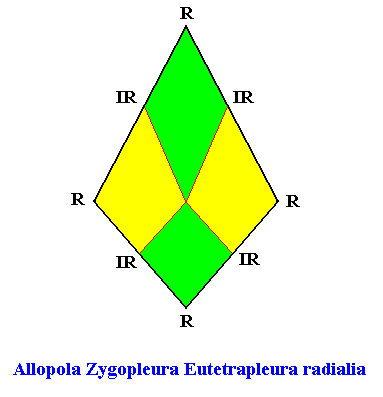
or, another, but equivalent representation (with straight interradial cross axes) :
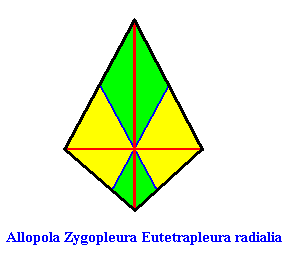
As one can see, the geometric figure representing this promorph consists of two isosceles triangles connected base to base.
Examples of holomorphic crystals :

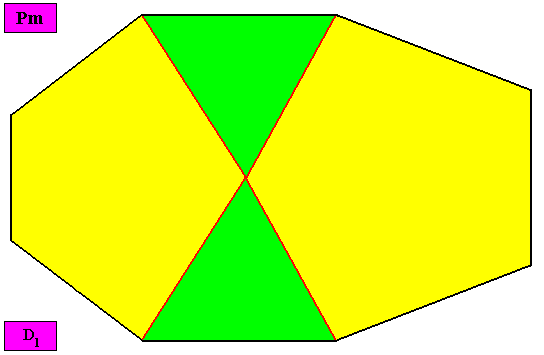Non-eupromorphic crystal
Intrinsic shape :  Bilateral Octagon
------------------------------------------------
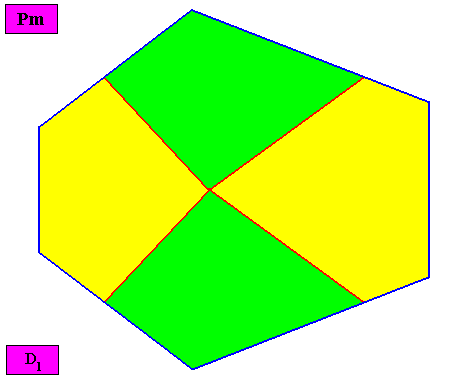Non-eupromorphic crystal
Intrinsic shape :  Bilateral Hexagon
------------------------------------------------
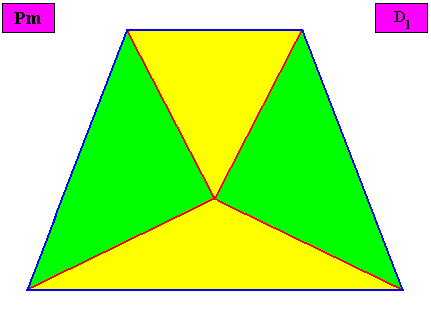Eupromorphic crystal
Intrinsic shape :  Bilateral Tetragon
------------------------------------------------

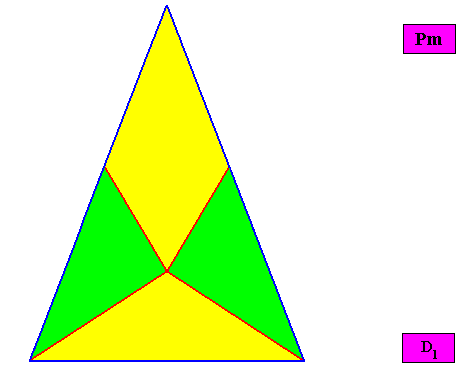
Non-eupromorphic crystal
Intrinsic shape :  Bilateral Trigon
Eutetrapleura interradialia

(zygopleura with four antimers and interradial directional axes,  isosceles trapezia)
Planimetric Basic Form, representing this promorph :
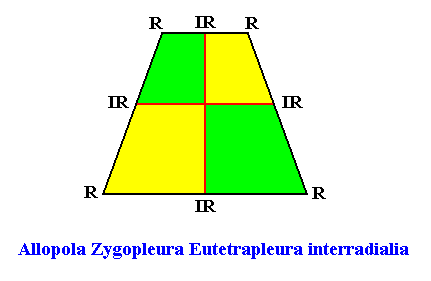
or, another, but equivalent representation (with straight radial cross axes) :
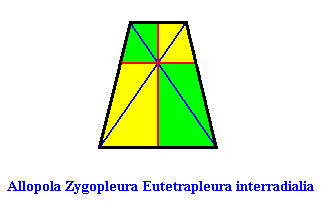
Examples of holomorphic crystals :

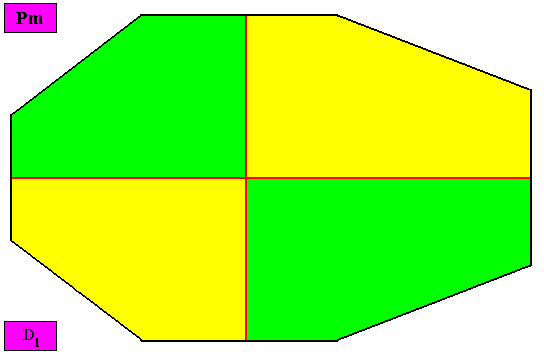Non-eupromorphic crystal
Intrinsic shape :  Bilateral Octagon
---------------------------------------------
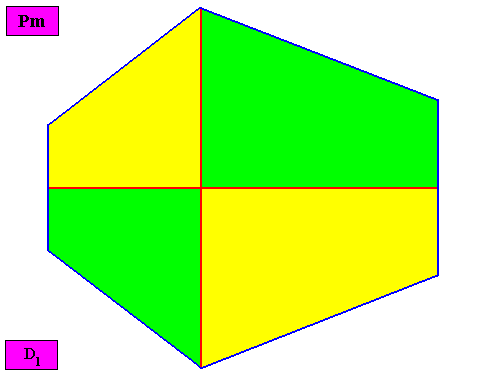Non-eupromorphic crystal
Intrinsic shape :  Bilateral Hexagon
----------------------------------------------
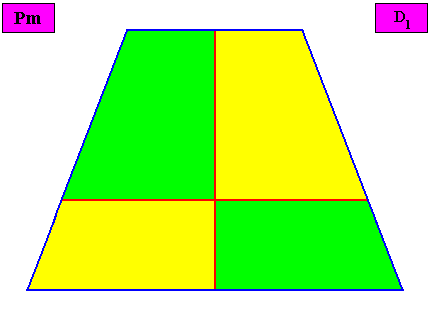Eupromorphic crystal
Intrinsic shape :  Bilateral Tetragon
-----------------------------------------------

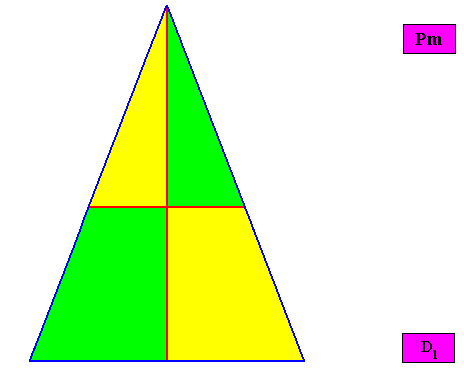
Non-eupromorphic crystal
Intrinsic shape :  Bilateral Trigon
Heterostaura Allopola (half amphitect polygons,  bilateral forms),
Allopola zygopleura (half rhombic polygons [i.e. isosceles triangles], or isosceles trapezia [i.e. bilateral tetragons] ;  bilateral forms with four or two antimers),
Zygopleura dipleura (symmetric or asymmetric zygopleura with two antimers :  eudipleura or dysdipleura) :
Zygopleura eudipleura

(isosceles triangles,  symmetric zygopleura with two antimers,  bilateral forms s.str.)
Planimetric Basic Form, representing this promorph :
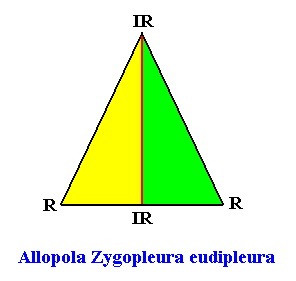
Examples of holomorphic crystals :

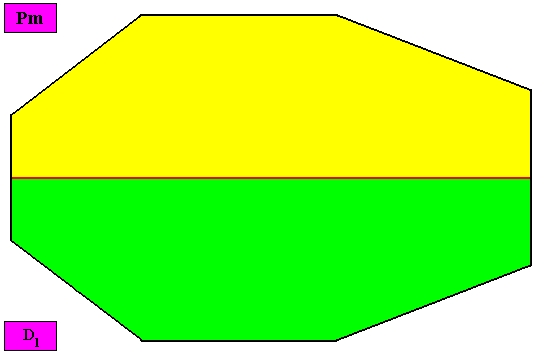Non-eupromorphic crystal
Intrinsic shape :  Bilateral Octagon
----------------------------------------------
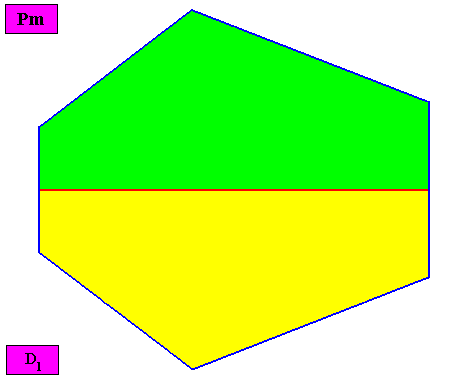Non-eupromorphic crystal
Intrinsic shape :  Bilateral Hexagon
-----------------------------------------------
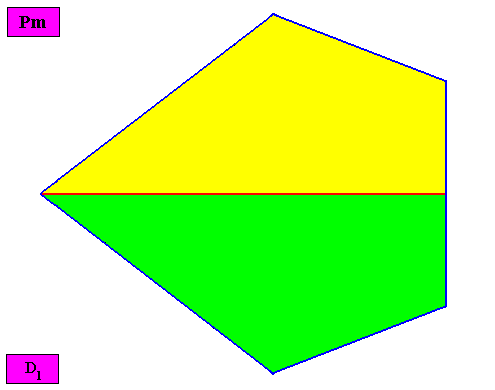Non-eupromorphic crystal
Intrinsic shape :  Bilateral Pentagon
------------------------------------------------
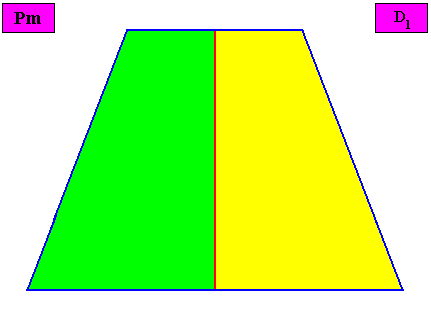Non-eupromorphic crystal
Intrinsic shape :  Bilateral Tetragon
-----------------------------------------------

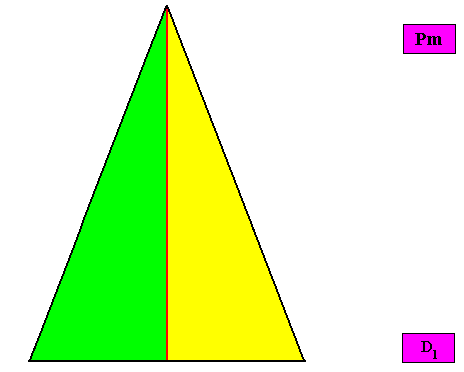
Non-eupromorphic crystal
Intrinsic shape :  Bilateral Trigon
A two-dimensional crystal with intrinsic shape according to an isosceles triangle and possessing two antimers, can also be considered as being an  eupromorphic  crystal, because the presence of two antimers cannot be expressed by a planimetric figure (consisting of straight lines) with two corners or two sides, because such a figure cannot exist. The simplest two-dimensional figure consisting of straight lines -- the "simplex figure" of two-dimensional space -- is a triangle. So the presence of two congruent antimers, related to each other by a mirror line, must be expressed by a triangle, to be more specific, by an isosceles triangle (because an equilateral triangle expresses three equal antimers, while an irregular triangle expresses two non-congruent antimers).
Anaxonia acentra / Zygopleura dysdipleura

(quarter-rhombi, i.e. right-angled triangles,  or asymmetric zygopleura with two (unequal) antimers,  irregular triangles)
Planimetric Basic Forms, representing these two promorphs :
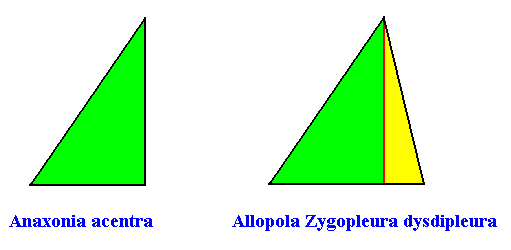
Examples of holomorphic crystals

No antimers (Anaxonia acentra) :

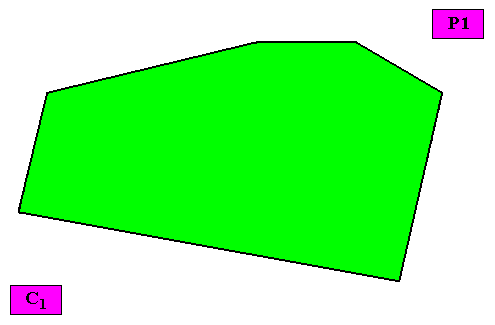Non-eupromorphic crystal
Intrinsic shape :  Irregular Hexagon (representing all irregular two-dimensional crystal shapes)
Two antimers.

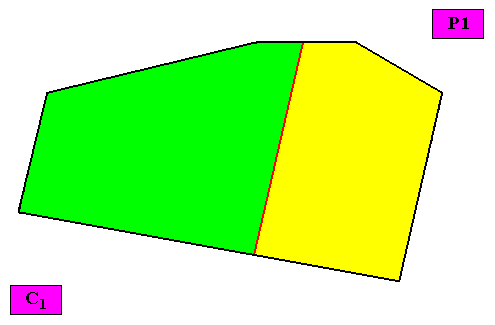Non-eupromorphic crystal
Two non-congruent antimers (green, yellow)
Intrinsic shape :  Irregular Hexagon (representing all two-dimensional crystal shapes)
This concludes our summaries of the foregoing results with respect to (more) complex two-dimensional crystal shapes.
While in the foregoing documents promorphs of two-dimensional crystals were studied from the viewpoint of intrinsic point symmetry, i.e. symmetry without translations or translational components, in documents to come we will study these promorphs from the viewpoint of their total intrinsic symmetry, i.e. all their symmetries, including translations and translational components.
But before we do this, we will dwell for a while in the ontological context of all these symmetry and promorphological studies (next document) :  We will once again investigate what role is played by Shape, Symmetry and Promorph in the layered structure of Being. And we present this investigation as a preliminary ontological discussion.

e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX (Sequel-1, Ontological Discussion).

Back to Homepage

Back to Contents

Back to Part I

Back to Part II

Back to Part III

Back to Part IV

Back to Part V

Back to Part VI

Back to Part VII

Back to Part VIII

Back to Part IX

Back to Part X

Back to Part XI

Back to Part XII

Back to Part XIII

Back to Part XIV

Back to Part XV

Back to Part XV (Sequel-1)

Back to Part XV (Sequel-2)

Back to Part XV (Sequel-3)

Back to Part XVI

Back to Part XVII

Back to Part XVIII

Back to Part XIX

Back to Part XX

Back to Part XXI

Back to Part XXII

Back to Part XXIII

Back to Part XXIV

Back to Part XXV

Back to Part XXVI

Back to Part XXVII

Back to Part XXVIII