e-mail :
This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Amphitect Gyroid Octagon
The next two Figures give a holomorphic two-dimensional crystal having as its intrinsic shape that of an amphitect gyroid octagon. It is holomorphic because the symmetry of its intrinsic shape is the same as the intrinsic (crystallographic) point symmetry of the crystal ( The intrinsic symmetry of an amphitect gyroid octagonal crystal can be different, namely according to the group C1 , but, because we now only consider holomorphic crystals, we have set the intrinsic symmetry to be that of C2 , i.e. we have set this symmetry to be the same as the symmetry of the intrinsic shape). This point symmetry, as set according to the group C2 , is as such implied by the crystal's plane group symmetry, which is according to the group P2 : the crystal consists of a periodic stacking of parallelogrammatic building blocks each containing in its center a motif with C2 symmetry (In the present case empty building blocks can already represent all by themselves a C2 motif. Nevertheless, a C2 motif is explicitly inserted for reasons of clarity.).
Figure above : Microscopic view of a two-dimensional C2 crystal (plane group P2) with the intrinsic shape of an amphitect gyroid octagon. Each parallelogrammatic building block contains in its center a C2 motif (black, consisting of two motif units, related to each other by a half-turn about the center of the building block).
Figure above : Same as previous Figure. The eight crystal 'faces' are indicated (dark blue lines). Recall that the building blocks are actually very small indeed, resulting in all the crystal faces being perfectly smooth.
The next Figure gives a macroscopic view of the crystal of the previous Figures, by omitting the lattice connection lines (delineating building blocks) and the motifs.
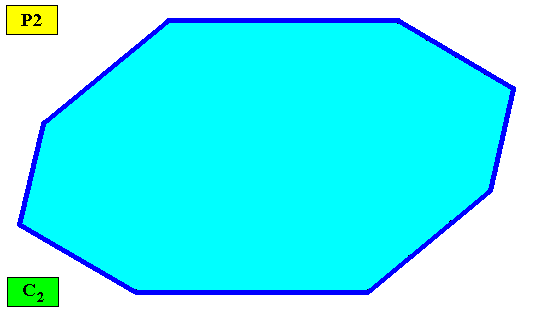
Figure above : Macroscopic view of the two-dimensional C2 crystal (plane group P2) with the intrinsic shape of an amphitect gyroid octagon.
The pattern of symmetry elements (with respect to the point symmetry) is given in the next Figure. It consists of one two-fold rotation axis only.
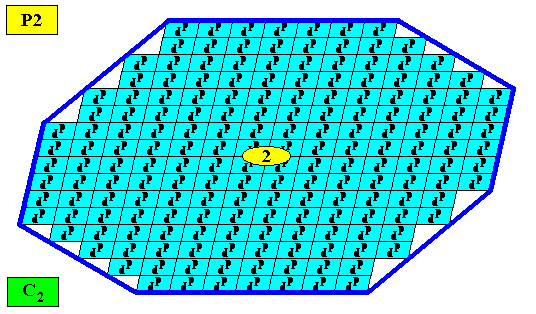
Figure above : Pattern of symmetry elements of the above two-dimensional C2 crystal having as its intrinsic shape an amphitect gyroid octagon. It consists of one 2-fold rotation axis (indicated by a small yellow ellipse) only.
The next Figure shows that four (crystallographic) Forms are needed to construct the outline of the above crystal.
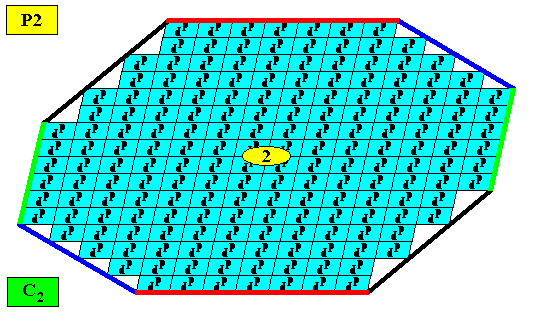
Figure above : Four Forms are needed to conceptually construct the (faces of the) above crystal : An initially given face implies one more face in virtue of the2-fold rotation axis. The result is one Form consisting of two faces. Four such forms are needed. They are indicated by the colors red, dark blue, green and black.
Possible a n t i m e r c o n f i g u r a t i o n s of a holomorphic two-dimensional crystal with intrinsic point symmetry according to the group C2 and an intrinsic shape according to an amphitect gyroid octagon.
The number and arrangement of a n t i m e r s in a crystal depend on the geometry of its translation-free residue. This residue is the motif as it remains after having everything 'telescoped in', i.e. after elimination of all translational elements in the crystal.
In the above Figures that would mean that the translation-free residue is the following :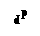 
. And here we clearly have to do with two antimers. However, in the present document (concerning C2 crystals) we will interpret motifs, as they are drawn in the ensuing Figures, not as motifs just like that, but as only r e p r e s e n t i n g the existence of a C2 motif w i t h a n y p o s s i b l e n u m b e r o f a n t i m e r s .
The precise relation of antimers and the internal structure of the crystal will be studied in later Parts.
Eight antimers.
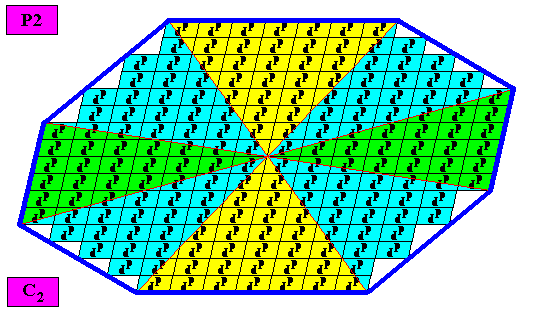
Figure above : The case of e i g h t similar antimers (green, yellow, blue) in a two-dimensional C2 amphitect gyroid octogonal crystal. ( The inserted C2 motifs have -- as they are drawn here -- only two antimers (represented by two motif units related to each other by a half-turn), but are, in the present case, meant to represent C2 motifs with eight antimers). The Vector Rosette of Actual Growth is supposed to coincide with the boundary lines of the antimers, letting the crystal be eupromorphic (But also when the vectors of the mentioned Rosette coincide with the median lines of the antimers, or correspond in some other way with the antimers, the crystal is eupromorphic).
The next Figure gives a macroscopic view of this crystal, by removing the lattice connection lines and the motifs.
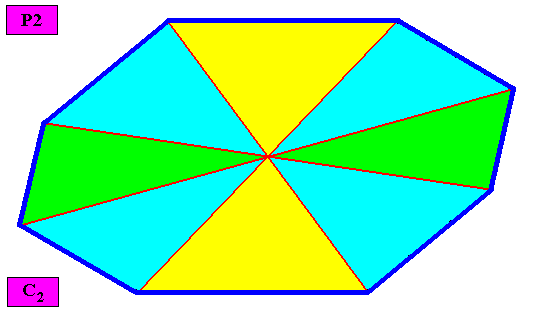
Figure above : Macroscopic view of the above two-dimensional C2 amphitect gyroid octogonal crystal with eight similar antimers (green, yellow, blue).
The promorph of the (eupromorphic) crystal of the previous Figures is belonging the Heterogyrostaura octomera. This promorph is depicted in the next Figure.
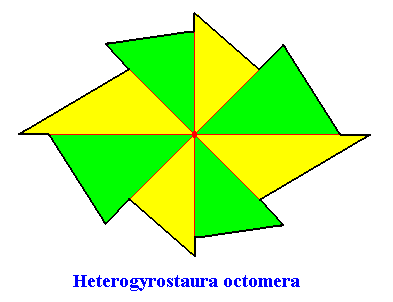
Figure above : Possible representation of the promorph of the above discussed two-dimensional C2 amphitect gyroid octogonal crystal with eight similar antimers. It is an eight-fold amphitect gyroid polygon, and as such the two-dimensional analogue of an eight-fold amphitect gyroid pyramid (which represents the promorph of corresponding three-dimensional crystals or other objects). To represent this promorph geometrically, we could have chosen a somewhat simpler figure -- in fact we can use the drawing of the crystal itself, without motifs and building blocks, and thus its macroscopic view as given above. We have nevertheless decided for the present figure because it emphasizes very clearly the gyroid nature of the polygon.
Six antimers.
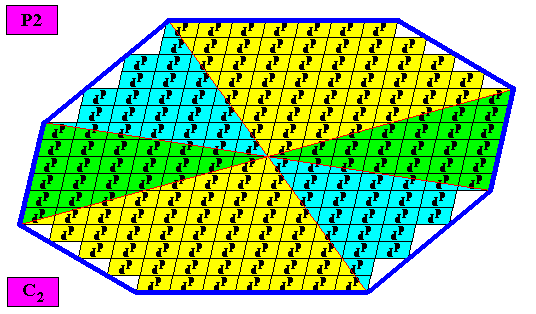
Figure above : A two-dimensional C2 amphitect gyroid octogonal crystal. The case of six similar antimers (green, yellow, blue). The crystal is non-eupromorphic because its intrinsic shape suggests eight antimers while in fact there are six.
The next Figure gives a macroscopic view of this crystal, by removing the lattice connection lines and the motifs.
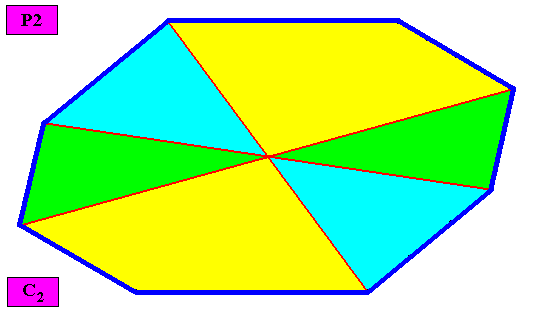
Figure above : Macroscopic view of the above two-dimensional C2 amphitect gyroid octogonal crystal with six similar antimers (green, yellow, blue).
The promorph of the crystal of the previous Figures is belonging to the Heterogyrostaura hexamera. It is depicted in the next Figure.
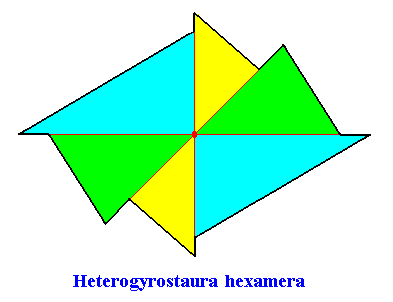
Figure above : Possible representation of the promorph of the above discussed two-dimensional amphitect gyroid octogonal C2 crystal with six antimers. It is an amphitect gyroid six-fold polygon (six antimers, green, yellow, blue), and as such the two-dimensional analogue of the amphitect gyroid six-fold pyramid, which is the promorph of corresponding three-dimensional crystals or other objects.
Four antimers.
Figure above : A two-dimensional C2 amphitect gyroid octogonal crystal. The case of four similar antimers (yellow, blue). The crystal is non-eupromorphic because its intrinsic shape suggests eight antimers while in fact there are only four.
The next Figure gives a macroscopic view of this crystal, by removing the lattice connection lines and the motifs.
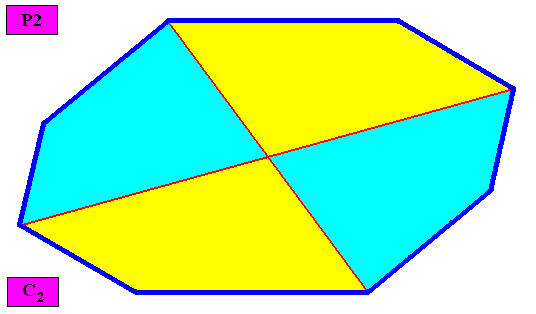
Figure above : Macroscopic view of the above two-dimensional C2 amphitect gyroid octogonal crystal with four similar antimers (yellow, blue).
The promorph of the crystal of the previous Figures is belonging to the Heterogyrostaura tetramera. It is depicted in the next Figure.
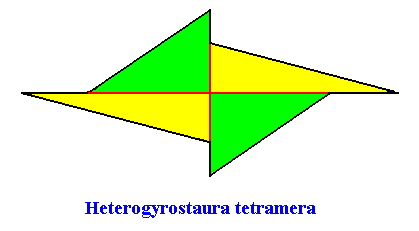
Figure above : The promorph of a two-dimensional amphitect gyroid octogonal C2 crystal with four similar antimers. It is a 4-fold amphitect gyroid polygon, and as such the 2-D analogue of a 4-fold amphitect gyroid pyramid, which is the promorph of corresponding three-dimensional crystals or other objects.
Two antimers.
Figure above : A two-dimensional amphitect gyroid octogonal C2 crystal with two equal antimers (yellow, blue, related to each other by a half-turn) ( The inserted C2 motifs have -- as they are drawn here -- two antimers, and are, in the present case, also meant to represent C2 motifs with two antimers). The crystal is non-eupromorphic because its intrinsic shape suggests eight antimers while in fact there are only two.
The next Figure gives a macroscopic view of this crystal, by removing the lattice connection lines and the motifs.
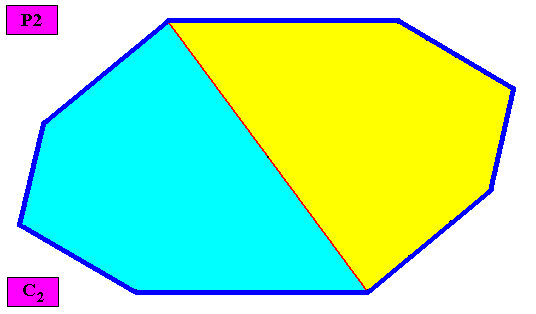
Figure above : Macroscopic view of the above two-dimensional C2 amphitect gyroid octogonal crystal with two equal antimers (yellow, blue).
The promorph of the crystal of the previous Figures is belonging to the Heterogyrostaura dimera. This promorph is depicted in the next Figure.
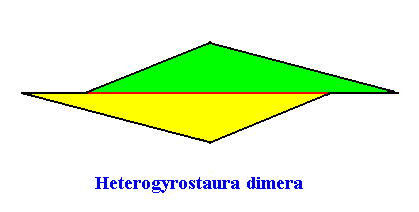
Figure above : The promorph of a two-dimensional amphitect gyroid octogonal C2 crystal with two equal antimers. It is a 2-fold amphitect gyroid polygon (i.e. an anmphitect polygon meant to represent two antimers), and as such the 2-D analogue of a 2-fold amphitect gyroid pyramid, which is the promorph of corresponding three-dimensional crystals or other objects.
In the next document we will discuss the third crystal shape of our list (as given in the previous document) , viz. the amphitect hexagon, with respect to intrinsic symmetry and promorph in holomorphic two-dimensional crystals having this shape intrinsically.
e-mail :
To continue click HERE for further study of the Theory of Layers, Part XVIII.
e-mail :