

e-mail :

This document continues the investigation of special categories (If / Then constants), and compares crystals with organisms.
Crystals and Organisms, Shape, Symmetry and Promorph.
Sequel to the investigation of some (intrinsic) shapes of two-dimensional crystals regarding their relationship to intrinsic point symmetry and promorph.
Regular Gyroid Ditetragon
We will now investigate two-dimensional crystals with an intrinsic shape according to a regular gyroid ditetragon as to their possible promorphs, but, as in the foregoing, limiting ourselves to holomorphic crystals, which means that we will only investigate crystals of which their intrinsic symmetry is the same as the symmetry of their intrinsic shape. In the present case this means that our regular gyroid ditetragonal crystals will have C4 intrinsic symmetry (while in other cases -- meromorphic crystals -- this symmetry could be according to C2 (Cyclic Group of order 2) or according to C1 (the Asymmetric Group), depending on the crystal's internal structure).

Figure above : Microscopic view of a two-dimensional crystal having as its intrinsic shape that of a regular gyroid ditetragon. Only empty building blocks are shown. Each building block is a square (which, as such, i.e. as empty square, can represent a D4 motif). If each one of them is provided with a motif that has C4 symmetry, the total symmetry is then according to the plane group P4. In that case the crystal is holomorphic, because its intrinsic point symmetry (C4 ) is the same as the symmetry (C4 ) of its intrinsic shape (regular gyroid ditetragon). A meromorphic crystal having this shape (intrinsically) could have an intrinsic symmetry according to the group C2 (which is a subgroup of C4 ) if the motifs of the building blocks have C2 symmetry (and not C4 symmetry). The plane group is then P2. If the motifs only have C1 symmetry (i.e. if they are totally asymmetric), then the intrinsic point symmetry of such a meromorphic crystal is according to the group C1 (Asymmetric Group) (which also is a subgroup of the group C4 ), and the plane group is then P1. However, in the present investigation we consider holomorphic crystals only. See next Figures.
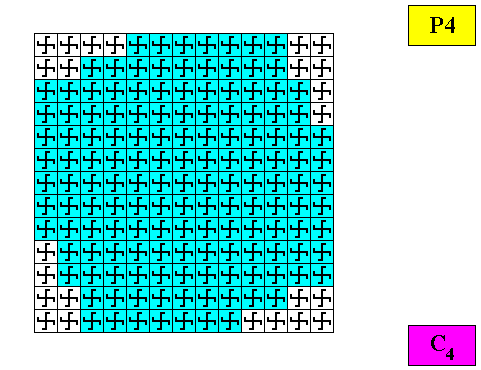
Figure above : Construction of a two-dimensional crystal (microscopic view) having as its intrinsic shape that of a regular gyroid ditetragon. C4 motifs (black) are inserted, resulting in a total symmetry according to the plane group P4, which in turn implies a point symmetry according to the cyclic group C4 .

Figure above : Result of the above construction of a two-dimensional crystal (microscopic view) having as its intrinsic shape that of a regular gyroid ditetragon and possessing an intrinsic symmetry according to the group C4 .
The next Figure indicates the 'faces' of the constructed crystal.
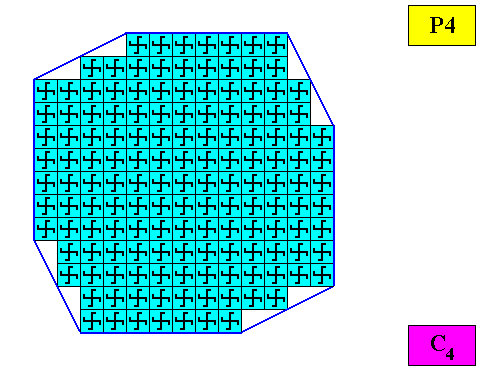
Figure above : Microscopic view of the two-dimensional crystal having as its intrinsic shape that of a regular gyroid ditetragon, as was constructed above. Crystal 'faces' indicated (dark blue lines).
In the next Figure the lattice lines (indicating building blocks) are removed, leaving the crystal with its microscopic motifs (which are periodically repeated according to the square point lattice, which had been indicated by connection lines in the previous Figure).
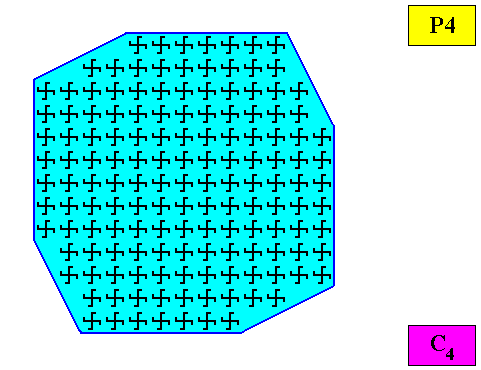
Figure above : The two-dimensional regular gyroid octogonal C4 crystal of the previous Figure. Lattice lines omitted.
By also removing the motifs, we obtain a macroscopic view of the crystal :
Figure above : Macroscopic view of the regular gyroid octogonal crystal of the Figures above.
The pattern of symmetry elements (with respect to the point symmetry) of our regular gyroid octogonal C4 two-dimensional crystal is given in the next Figure.
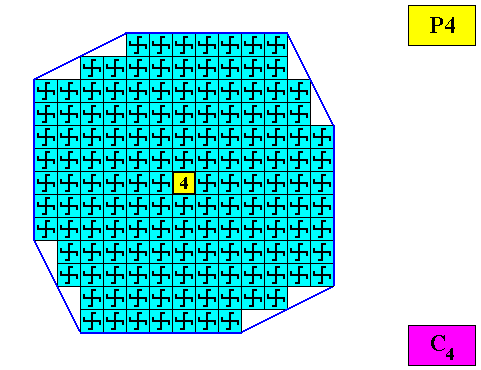
Figure above : Pattern of symmetry elements of the above given regular gyroid octogonal C4 two-dimensional crystal. Its consists of one 4-fold rotation axis (yellow) only.
Two crystallographic Forms are needed to construct the outline of the regular gyroid octogonal crystal, as the next Figure shows.
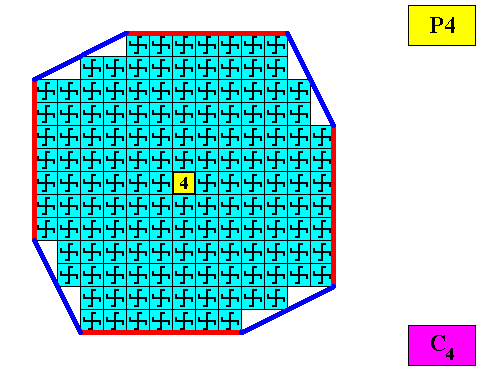
Figure above : Two crystallographic Forms (red, dark blue) are needed to construct the faces of our regular gyroid octogonal C4 two-dimensional crystal : An initially given face (red) implies three more faces in virtue of the 4-fold rotation axis, resulting in one closed Form (a square) consisting four faces (red). In the same way a second initially given face (dark blue) also gives rise to a closed Form (a second Form), which also consists of four faces together forming a square. These two Forms combine to give our regular gyroid octogonal crystal.
Possible a n t i m e r c o n f i g u r a t i o n s for holomorphic regular gyroid octogonal two-dimensional crystals.
Four antimers.
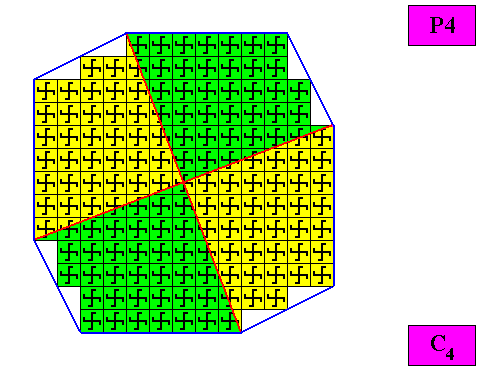
Figure above : A regular gyroid ditetragonal C4 two-dimensional crystal. The case of f o u r equal antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a C4 motif (black) inside each quadratic building block. It is -- or represents -- an atomic configuration such that four equal antimers (related to each other by a 4-fold rotation axis) can be distinguished in it. The crystal is non-eupromorphic because its intrinsic shape suggests eight antimers, while in fact there are only four.
Removing the lattice connection lines and the motifs, results in a macroscopic view of the crystal :
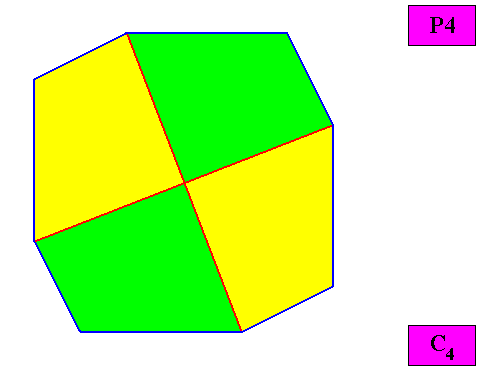
Figure above : Macroscopic view of the regular gyroid octogonal C4 two-dimensional crystal of the previous figure, with four equal antimers (green, yellow).
The promorph of the above gyroid non-eupromorphic crystal is (as two-dimensional analogue) belonging to the Homogyrostaura tetramera. This promorph is depicted in the next Figure.
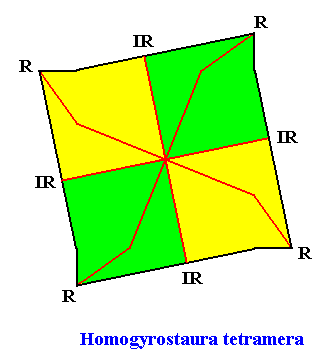
Figure above : The promorph of the regular gyroid octogonal C4 crystal with four antimers. It is a regular gyroid 4-fold polygon and as such the two-dimensional analogue of the regular gyroid 4-fold pyramid (See next Figure) which represents the promorph of corresponding three-dimensional crystals or other objects. Note the similarity of shapes between this promorph (regular gyroid 4-fold polygon) and that of the crystal (regular gyroid ditetragon) of which it is the promorph. In fact the depicted shape of our crystal can represent the promorph perfectly well. However, in our present drawing of the promorph (representing all Homogyrostaura tetramera) the gyroid nature is expressed more suggestively.
Radial (R) and interradial (IR) directions are indicated.
If we omit the four buckled lines (that only serve to emphasize the gyroid nature) ending up in the corners, we have this same promorph, where its four equal antimers are indicated by the colors green and yellow :
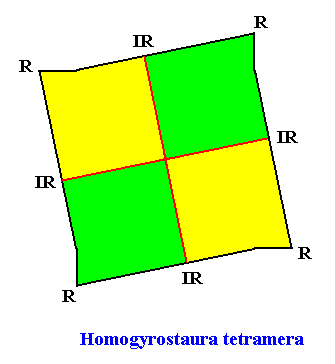
Figure above : The promorph of the regular gyroid octogonal C4 crystal with four antimers. Buckled auxiliary lines omitted.
The three-dimensional counterpart of this promorph is depicted in the next Figure.
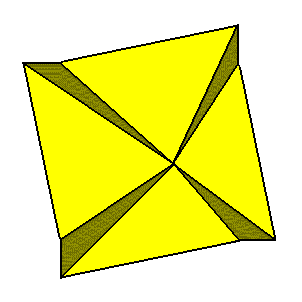
Figure above : Regular gyroid 4-fold pyramid (slightly oblique top view), representing all three-dimensional Homogyrostaura tetramera (i.e. all regular 4-fold gyroid promorphs of three-dimensional objects).
A holomorphic two-dimensional crystal having the shape of a regular gyroid ditetragon (depicted in the Figures above) has an intrinsic symmetry according to the group C4 because this is the symmetry of its intrinsic shape. This intrinsic symmetry (C4 ) allows for only 4n antimers to be present. When n = 1, as in the above case, the (four) antimers are equal, because they can be transformed into each other by a mechanical operation, in the present case by a 4-fold rotation axis. If n is different from 1, the antimers are not equal, but similar.
Meromorphic. Two antimers.
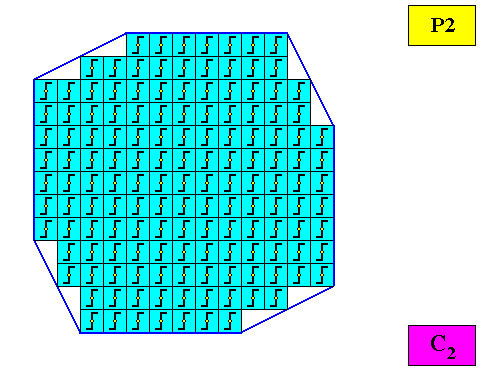
Figure above : A regular gyroid octogonal C2 two-dimensional meromorphic crystal. Its C2 motifs (black) have two equal antimers.
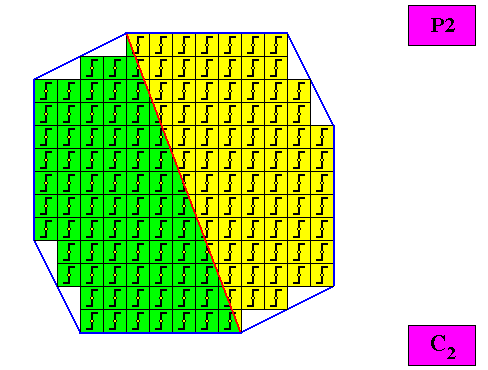
Figure above : The regular gyroid octogonal C2 two-dimensional meromorphic crystal of the previous Figure. The case of t w o equal antimers (green, yellow), related to each other by a 2-fold rotation axis. Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a C2 motif (black) inside each quadratic building block. It is -- or represents -- an atomic configuration such that two antimers (related to each other by a half-turn) can be distinguished in it. The crystal is meromorphic because its intrinsic symmetry (C2 ) is different from (namely lower than) the symmetry of its intrinsic shape. The crystal is non-eupromorphic because its intrinsic shape suggests eight antimers, while in fact there are only two.
Removing the lattice connection lines and the motifs, results in a macroscopic view of the meromorphic crystal :
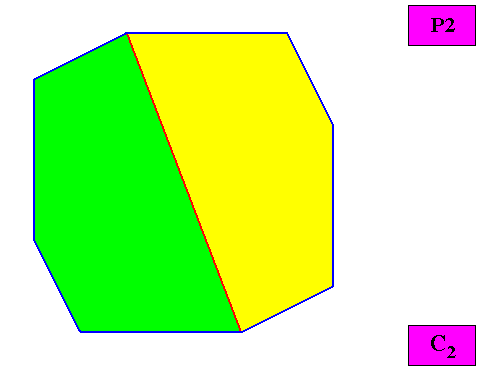
Figure above : Macroscopic view of the meromorphic regular gyroid octogonal C2 two-dimensional crystal of the previous figure, with two equal antimers (green, yellow).
The promorph of the above gyroid non-eupromorphic crystal belongs (as two-dimensional analogue) to the Heterogyrostaura dimera. This promorph is depicted in the next Figure.
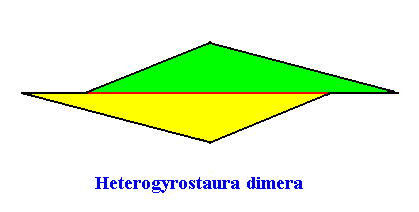
Figure above : The promorph of the meromorphic non-eupromophic regular gyroid octogonal C2 crystal with two antimers. It is a 2-fold (and therefore amphitect) gyroid polygon (i.e. an amphitect polygon meant to express the presence of two antimers) and as such the two-dimensional analogue of the 2-fold gyroid pyramid, which represents the promorph of corresponding three-dimensional crystals or other objects. Note the difference in shape between this promorph (2-fold gyroid polygon) and that of the crystal (regular gyroid ditetragon) of which it is the promorph.
As has been explained above, holomorphic two-dimensional crystals having as their intrinsic shape that of a regular gyroid ditetragon and thus implying their intrinsic symmetry to be according to the group C4 , can have only 4n antimers (In fact this holds for all C4 two-dimensional crystals). Above (i.e. in the beginning of the document) we discussed the case for n = 1, and now we will consider the case for n = 2, i.e. the case for eight antimers. These antimers cannot be equal, because that would imply the presence of an 8-fold rotation axis, while our crystal has, by definition, only a 4-fold rotation axis (and in addition to this, an 8-fold rotation axis cannot occur in crystals, whether they be two-dimensional or three-dimensional).
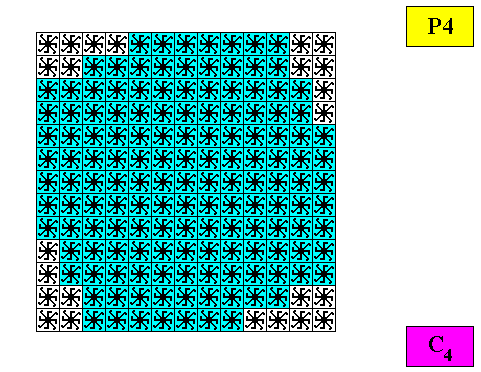
Figure above : Construction of a two-dimensional crystal (microscopic view) having as its intrinsic shape that of a regular gyroid ditetragon. Its C4 motifs (black) possess eight similar antimers. A pair of two similar antimers is repeated four times around the center of the motif, effecting that center to be a 4-fold rotation axis of the motif.

Figure above : Result of the above construction of a two-dimensional crystal (microscopic view) having as its intrinsic shape that of a regular gyroid ditetragon and possessing an intrinsic symmetry according to the group C4 .
The next Figure indicates the 'faces' of the constructed crystal.
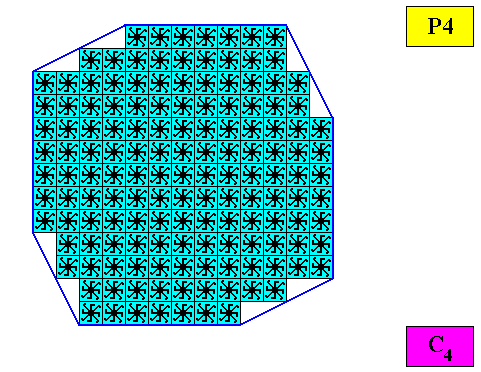
Figure above : Microscopic view of the two-dimensional crystal having as its intrinsic shape that of a regular gyroid ditetragon, as was constructed above. Crystal 'faces' indicated (dark blue lines). The motifs (black) possess eight similar (not equal) antimers.
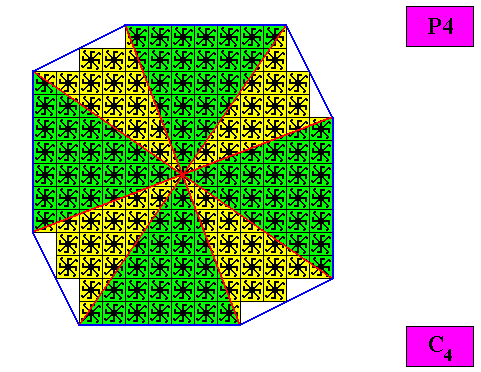
Figure above : The regular gyroid ditetragonal C4 two-dimensional crystal of the previous Figure. The case of e i g h t s i m i l a r (not equal) antimers (green, yellow). Although the antimers are not equal just like that, the set of eight antimers consists of two subsets of equal antimers (i.e. each subset consists of four equal antimers), such that the two types of antimers alternate. The degree of similarity of the antimers is considered to be sufficient for recognizing eight similar antimers instead of four equal (but larger) antimers. Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a C4 motif (black) inside each quadratic building block. It is -- or represents -- an atomic configuration such that eight similar antimers can be distinguished in it. They form four pairs of antimers, and these pairs are related to each other by four-fold rotation The crystal is eupromorphic because its intrinsic shape suggests eight similar antimers, which are indeed present.
Removing the lattice connection lines and the motifs, results in a macroscopic view of the crystal :
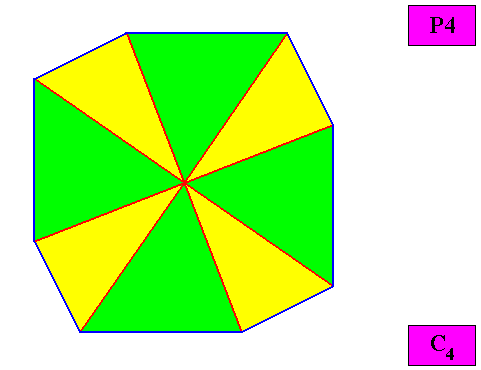
Figure above : Macroscopic view of the regular gyroid ditetragonal C4 two-dimensional crystal of the previous figure, with eight similar antimers (green, yellow).
The promorph of the above gyroid eupromorphic crystal belongs (as two-dimensional analogue) to the Homogyrostaura ditetramera. This promorph is depicted in the next Figure.
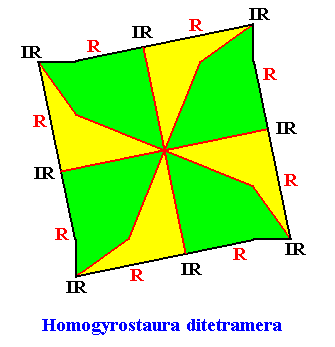
Figure above : The promorph of the regular gyroid octogonal C4 crystal with eight similar antimers. It is a regular gyroid 4-fold polygon (here meant to express the presence of 8 (2x4) similar antimers) and as such the two-dimensional analogue of the regular gyroid 4-fold pyramid (here expressing eight similar three-dimensional antimers) which represents the promorph of corresponding three-dimensional crystals or other objects. Note the similarity of shapes between this promorph (regular gyroid 4-fold polygon with eight similar antimers) and that of the crystal (regular gyroid ditetragon) of which it is the promorph. In fact the depicted shape of our crystal can represent the promorph perfectly well as soon as the eight similar antimers are indicated in it (as was done in the previous Figure). However, in our present drawing of the promorph (representing all Homogyrostaura ditetramera) the gyroid nature is expressed more suggestively.
Radial (R) and interradial (IR) directions are indicated. Compare with the promorph that belongs to the Homogyrostaura tetramera depicted above.
The next Figures again depict a two-dimensional regular gyroid octogonal crystal of which the translation-free residue (motif) possesses eight very dissimilar 'antimers'. The very strongly expressed dissimilarity is sufficient to not consider the residue to consist of eight (similar) antimers, but of four equal antimers, each consisting of two dissimilar structures, together forming one antimer. This implies that this crystal is non-eupromorphic because its intrinsic shape suggests eight similar antimers, while in fact there are four equal antimers.
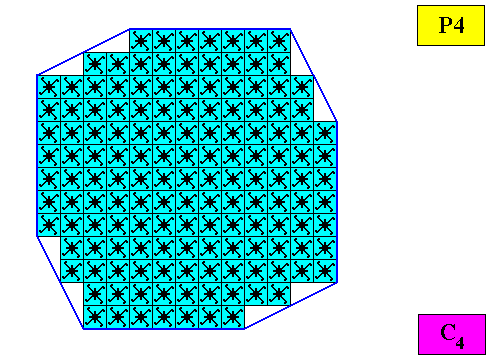
Figure above : A regular gyroid ditetragonal C4 two-dimensional crystal. Its C4 motifs seemingly have eight similar antimers. In fact, however, they are very dissimilar. So they must be conceived as pairs, consisting of two dissimilar structures, and only such a pair should be considered to represent an antimer. And the antimer, so conceived, is repeated four times around the center of the motif.
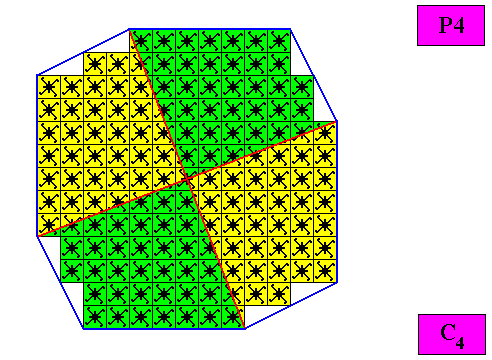
Figure above : The regular gyroid ditetragonal C4 two-dimensional crystal of the previous Figure. The case of f o u r equal antimers (green, yellow). Note the correspondence between the morphology of the (microscopic) motif (as translation-free residue) and the arrangement of the (macroscopic) antimers of the crystal. In this way the promorph, and in particular the number of antimers is based on the morphology of the translation-free residue of the crystal. This residue is explicitly given in the form of a C4 motif (black) inside each quadratic building block. It is -- or represents -- an atomic configuration such that four equal antimers (related to each other by a 4-fold rotation axis) can be distinguished in it. The crystal is non-eupromorphic because its intrinsic shape suggests eight antimers, while in fact there are only four.
Removing the lattice connection lines and the motifs, results in a macroscopic view of the crystal :

Figure above : Macroscopic view of the regular gyroid octogonal C4 two-dimensional crystal of the previous figure, with four equal antimers (green, yellow).
The promorph of the above gyroid non-eupromorphic crystal is (as two-dimensional analogue) belonging to the Homogyrostaura tetramera (and not ditetramera, or octomera for that matter). This promorph is depicted in the next Figure (and was already depicted earlier).

Figure above : The promorph of the regular gyroid octogonal C4 crystal with four antimers, where the presence of these four antimers was based on a complex translation-free residue seemingly possessing eight similar antimers, but in fact possessing only four antimers. This promorph is a regular gyroid 4-fold polygon and as such the two-dimensional analogue of the regular gyroid 4-fold pyramid which represents the promorph of corresponding three-dimensional crystals or other objects.
In the next document we will discuss the eleventh crystal shape of our list (as given in Part XVI ) , viz. the regular ditetragon, with respect to intrinsic symmetry and promorph in holomorphic two-dimensional crystals having this shape intrinsically.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXVI.