

(Takes a little while loading the images)
e-mail :

Sequel-10 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-10) further elaborates on the analogy between crystals and organisms.
The Theory of Organic Lattices
Introduction.
In organisms we often see an underlying point symmetry beneath its superficial asymmetric shape. It is described by Promorphology in Second Part of Website .
Also some 'awareness' of specific location within the body -- cells must 'know' where they are in the multicellular body, and intracellular structures must 'know' where they are in the body of unicellular organisms -- must be 'experienced' by the organism, which means that there must be some localization-medium within the organismic body.
These two aspects constitute the main problem of organic morphogenesis, and can be subsumed under the heading of
" The problem of the organized spatial distribution of elements within the organismic body".
We can also call it the problem of scalar and vectorial regularities of an organismic body, where scalar regularity means the occurrence of a constant number of equivalent macroscopic elements or units making up the body or parts of it, and where vectorial regularity means that certain definite directions within the orgamismic body stand out, resulting in definite body axes that make definite angles with each other, causing the body to be anisotropic.
A third problem, connected with these two, is the enormous form potential that is evident in organisms : almost every shape and pattern seems to be realized in the world of organisms.
How could we, if it only were in the form of a preliminary hypothesis, explain this spatial organization in organisms? Many theories and ideas have been proposed, but none has been generally accepted.
We think that the discovery of non-equilibrium crystallization, as was discussed in the previous documents, could be the key to the understanding (if only in a global preliminary way) of the spatial organization in the organismic body.
The form-generating potential of the system "Chemically filled-in Lattice plus Fast Unstable Growth" is enormous, almost without limit, as we've seen in the case of ice (snow crystals, windowpane frost, etc.). We have also seen that a crystal has holistic properties just as it is also assumed (by many authors) for organisms.
All this has resulted for us to propose the Theory of Organic Lattices (first proposed by PRZIBRAM in 1926). So according to this theory the organismic body contains an organic lattice. We must say "contains" (and not "is") because of the fact that apart from the lattice elements, also other constituents are present in the organismic body (while crystals just are chemical entities arranged according to some lattice, and nothing more).
But how must we imagine such an organic lattice to look like? Organisms are mechanically flexible entities that result from a complex and literally convoluted morphogenesis, and are as such far from being crystals. And why was such an organic lattice never actually observed? How can such a lattice do its job (symmetry, localization) when it is constantly pervaded by other chemicals?
The answer is "analogy".
We cannot assume that an organism is just some complicated crystal, like, say, many silicate minerals are. Organisms are not just periodic structures, resulting from the close packing of identical chemical entities. They are highly heterogeneous. Their 'lattice' can at best be only analogous to that of crystals. We will call such an organic lattice an e l e v a t e d l a t t i c e. It is a sophisticated version of a(n inorganic) crystal lattice.
And indeed, it is well known that there are many analogies between crystals and organisms, like growth, individuality, specifity, regeneration ability, symmetry, etc. But they are, indeed, only analogies, pointing to some common underlying laws. But whereas these laws lie right at the 'surface' of crystals, they are buried and hidden away in organisms, i.e. in organisms they are harnessed in some way, in order to result in functionality and do away with randomness.
Organisms reside in a different ontological Layer or domain than Inorganisms do. They either involve the appearance of a CATEGORICAL NOVUM (i.e. involve an ontological novelty with respect to the Inorganic Layer) or at least are the result of a complexity jump (See Part I and See Part XXIX Sequel-1 ), that can be seen when we change from the Inorganic Layer to the Organic Layer.
And this "residing in different ontological domains" causes the correspondences between crystals (as intrinsic beings belonging to the Inorganic Layer) and organisms (as intrinsic beings belonging to the Organic Layer) to be just analogies, which means that organisms are, so to say, 'upgraded versions' of crystals.
As has been said, there are many analogies between crystals and organisms. And now we can say that just like growth in crystals is not the same, but only analogous to that in organisms, where the latter is much more sophisticated and controlled than it is in crystals, and just like individuality in crystals is not the same, but only analogous to that in organisms (especially higher organisms), and just like the ability to regenerate in crystals is not the same, but only analogous to that in organisms, we can (also) say that the lattice as it is in crystals is not the same as it is in organisms. The crystal lattice is only analogous to that in organisms. Thereby we must note that the "only analogous" only refers to the chemical, resp. physiological nature of the respective lattices. Geometrically they are identical : a lattice is a periodic arrangement of points in (geometric) space. For two-dimensional space there are five such point lattices (in the strict sense), while in three-dimensional space there are 14 different point lattices (in the strict sense).
If the point lattice is provided with chemical motifs, such that these motifs are now arranged according to this point lattice, then we have a (chemical) periodic s t r u c t u r e . And, depending on the symmetry of the motifs, we get 17 plane groups for two dimensions, and 230 space groups for three dimensions. These plane groups and space groups describe the t o t a l symmetry (and only the total symmetry) of the given periodic structure (Recall that a structure is periodic if it consists of identical building blocks that are stacked in a regular way all having the same orientation).
So our organic lattice is a 'sophisticated' well-controlled complex version of the crystal lattice. And this 'lattice' must be interpreted in a somewhat broader sense than a lattice in the strict sense (which means a strictly periodic structure) to include geometrically 'forbidden' symmetries, like 5-fold, 7-fold, etc. symmetries that occur in organisms. And so must our interpretation of "crystal " . If we do so we include (into the broadened concept of crystal) so-called quasi-crystals that can indeed have these forbidden symmetries.
The strength of the theory of organic lattices is that such a lattice can, like in crystals, emerge spontaneously from an initially isotropic medium, and thus can emerge without postulating some pre-existent vectoriality. Indeed, the reason that we invoke crystals to explain form generation in organisms is the following : If we are to explain the latter we must first resort to simpler phenomena, and these we find in the inorganic world. Now the only truly intrinsic and vectorial beings of the inorganic world that have a size comparable to that of organisms, are crystals. They indeed are intrinsic individuals with definite vectoriality, i.e. having within their body definite directions, differing from other directions within that same body. And it is vectoriality in organisms that have to be explained.
Below we will show what it exacly should mean that an organic lattice is a sophisicated version of a crystal lattice (Authors like PRZIBRAM, who first proposed the existence of organic lattices, thought about them as more or less straightforward crystal lattices, which, however, according to me, contradict known facts).
On making assumptions.
We must realize that our idea of an organic (quasi) lattice (i.e. either a genuine lattice, which is strictly periodic, or a quasi-lattice, which is approximately periodic), accounting for morphological lay-out, symmetry and position (within the developing organismic body), is highly hypothetic. Many assumptions must be made, for instance that the lattice formation is kept undisturbed by other chemical agents in the same environment within the organismic body. Further the embryo must choose a certain point through which crystallographic axes run, in order to establish the point symmetry of the developing organism, or at least to function as the origin of a coordinate system, implying 'counting' from this origin to determine the location of, say, a cell, within the organismic body. Further we must assume (see below) that, when the organism is as such still more or less folded during (some period of) its embryological state or in its pupal state (in the case of holometabolic insects), not only the geometric symmetry of the lattice is preserved, but also its chemical symmetry, which is supposed to be accomplished by compensating reactions. Such compensating reactions must also be assumed for neutralizing the effect of chemical agents that are not belonging to the organic lattice.
But despite these 'heavy' assumptions, that must be incorporated within the theory of organic lattices, we could feel more or less reassured by the fact that the spatial aspect of organic morphogenesis is still an unsolved problem in Biology. However, we must be aware not to invoke the organism's ability to regulate many many processes, to let it create anything we want. Where we call upon this ability in order to let it create a lattice, without this lattice's generation and maintenance being disturbed by other chemical agents (and thus physiologically let it [i.e. the organism] isolate this lattice), we are making an assumption. And an assumption ultimately needs to be demonstrated to represent an observed fact.
What precisely is an organic lattice, and in what way is it only analogous to a crystal lattice?
Because an organism is not a solid, but finds itself in a semi-liquid state, the organic lattice is, first of all, supposed to be a semi-solid crystal, i.e. a swollen crystal like we see in organic crystals (for exampe protein crystals) that have imbibed water, or (the organic lattice is) in some cases, an almost-solid crystal. In other cases, like in small Homaxonic (i.e. spherical) or Monaxonic (i.e. cylindrical, conic, and the like) organisms, it could be a (semi-)liquid crystal (which are only partly periodic), but in all cases such a crystal is masked by its being (partly) overruled, or even atrophied after it has served as an initial localization medium and now replaced by the subsequent morphological and chemical features that are part of the ultimate or penultimate structure of the organism. But in all mentioned cases (semi-solid crystal, almost-solid crystal, (semi-)liquid crystal) the lattice pattern can be supposed to consist of more or less static motifs, themselves consisting of static constituents : the whole lattice + motifs is a static pattern, like in real (solid) crystals.
On the other hand, a lattice + motifs could be supposed to be fully dynamic. It could be the result of a reaction-diffusion system known as Turing structures. BALL, P., Designing the Molecular World , 1994, p.313, writes about them :
What Turing showed theoretically was that these structures could form spontaneously in an autocatalytic system in which the reactant molecules diffuse at different speeds through the reaction medium -- a so-called reaction-diffusion system. Specifically, if the faster-traveling reactants inhibit the reaction whereas the slower ones catalyze it, then within a certain range of diffusion rates of the reactants the system can transform suddenly from a uniform mixture into one in which the chemical composition varies in a regular manner from place to place. In effect, the system turns into a kind of crystal, with periodic structure -- but a very peculiar kind of crystal, because all the molecules within it are free to move around yet the patterned structure remains. In a normal crystal, this freedom of movement would destroy any periodicity.
And so it could be, that, directed by a dynamic localization system -- as just described -- static structures appear. And such a dynamic periodic structure is only geometrically similar to a crystal lattice. It works quite differently, and thus is only analogous to a real crystal. Also its structural scale is probably larger than that of a true crystal. But despite these differences, its act of directing the organism's morphology (among others, by fast growth features), its act of determining the organism's point symmetry and providing for a localization medium within the organism's body, is the same, i.e. works in the same manner, as it is supposed to do in the case of its being a static lattice.
The (supposed) formation of an organic lattice, static or dynamic, in the early stages of (embryonic) development, can be seen as a symmetry-breaking process : a transition from the maximal symmetry of isotropic organic matter to a lower symmetry, for example that of a hexagonal array of chemical entities (which as such represents a lower symmetry than that of, say, a spherical drop of oil suspended in water).
Our theory of organic lattices first of all only accounts for the global point symmetry of the organism (or maybe -- if localized -- of certain parts of the organism). The morphological details must come about by adding fast unstable growth (as seen in non-equilibrium crystallization) or, perhaps by special processes of the activation-inhibition type (COVENEY, P. & HIGHFIELD, R, Frontiers of Complexity, 1995). We here concentrate mainly on global symmetry. We can see -- as has been said -- the organic lattice either as an underlying and more or less hidden semi-solid crystal (perhaps only present at the beginnings of individual development) or liquid crystal, or we can view it as the result of processes akin to those that produce lattices like Turing patterns. In the latter case the concentration profiles of such a pattern can serve as triggers that switch on or off genes (in multicellular organisms). Symmetric patterns (i.e. a symmetric distribution) of secondary (with respect to the underlying lattice like Turing structures) structures then develop, and take over the function of localization medium.
REMARK : The organic lattice, responsible for differential growth, regeneration ability, morphology and overall symmetry, could be something like the "ringmaster" in our brains (a ringmaster actually is a person which seemingly directs the performances in a circus by making all kinds of gestures, whereby he seems, for the audience, to be in charge but isn't) : In (the case of) a brain it is a high-level phenomenon, resulting from uncountable interactions (between neurons) on a low level, and in such a way representing an organizing entity, while it is not a specific entity to which one can point with the finger. The organic growth, regeneration and symmetry emerge from the many regulatory interactions and present the illusion as if there is one definite 'something' that directs this growth, etc. In order to understand differential growth we still can use this definite entity -- the organic lattice -- knowing, however, that it is an emergent not-localized something, that works as if there is indeed an organic lattice present. If this is correct, then this lattice is just as undetectable as is in fact our 'Self ' (i.e. also our Self is not some entity somewhere located within our body, it is just the imaginary 'ringmaster'). The overall effect of organic growth and regeneration is the same as if it really came from (the properties of) a concrete organic lattice. If this is correct then the status of the organic lattice is only that of a metaphor, which, however, does not reduce its importance (as concept) to nothing.
When the more or less detailed structure of the organism is finally formed, mainly in virtue of the system "Lattice + Fast (unstable) Growth" , the lattice can still persist (although it could, in some cases, be discarded by the organism). Let's look to the next Figure (already given earlier) where we see a detailed structure that has been generated by this system (lattice + fast growth) :

Figure above : Part of a snow crystal. Product of the system "Hexagonal Lattice (provided with H2O molecules) + Fast (unstable) Growth"
We see an intricate structure of ridges, grooves, narrow interruptions (i.e. the narrow space between the branches) and complex contours, and yet there is complete crystallographic continuity, i.e. there is one and the same lattice, in one and the same orientation, that, although not extending beyond the structure, pervades this whole structure.
(After LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
The organic lattice, as it is in itself, must be interpreted as a 'crystal'. When it grows in a non-equilibrium fashion it turns into a complex structure. This structure is, in itself, materially homogeneous, i.e. it is an arrangement of identical or equivalent chemical units, periodically stacked in such a way that a three-dimensional 'building' results, having a definite shape. See next diagram.
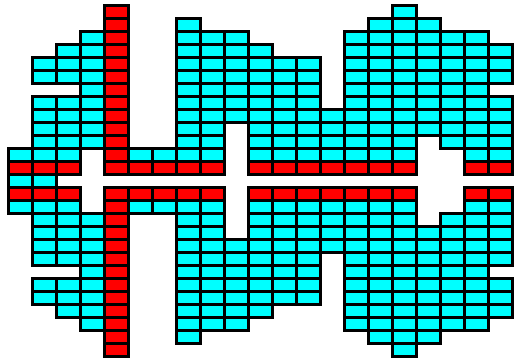
Figure above : In fact, any structure, any shape, can be built by periodically stacking pre-existing building blocks (i.e. units being arranged according to a certain lattice). The shape can be the result of non-equilibrium crystallization. And however complex this shape may be, the structure that carries it is crystallographically continuous, meaning that the structure is pervaded by one and the same lattice.
The red building blocks indicate possible stacking up into the third dimension. As such they represent ridges lying on top of the surface of the structure.
Such a chemically homogeneous structure can then serve as spatial matrix for substructures subsequently to be developed, ultimately leading to a morphologically full-fledged organism.
Of course the organic lattice (and its quasi-lattice variants) cannot be just a crystal lattice, because in that case there would be little space left for other molecules. The organism would then be just a crystal, which, of course, it isn't. As has been said, the organic lattice is not identical, but only analogous to that of a true crystal, it is, as we called it, an elevated lattice. And in working out the (stereochemical and geometric) nature of such an elevated lattice, we are forced to make several assumptions with which we now shall deal.
A real crystal is formed when chemical motifs try to get as close together as conditions permit in order to attain the lowest energy configuration. If the areas of (effective) mutual influence, or force patterns (each one of them surrounding a chemical motif), with respect to mutual attraction and repulsion of these motifs, are spherical, then these areas will spontaneously arrange into a pattern, a lattice, that is hexagonal in two dimensions (i.e. as a layer) and cubical or hexagonal in three dimensions. If, on the other hand, they have a different shape, i.e. when the force pattern of the motifs is anisotropic (different in different directions), especially a different symmetry, then these areas will arrange themselves into a different lattice. We can say that the motifs are represented by their areas of mutual influence. Overlap of these areas results in mutual repulsive forces, while separation of them results in mutual attractive forces. In a real crystal these areas of effective mutual influence are very small indeed. So the chemical motifs are packed close together (with their areas of effective influence always contiguous).
Because in an organism (and also in a developing embryo) there necessarily must be plenty of space available to other molecules and supramolecular structures, the spacing of the organic lattice must be significantly wider than that in real crystals. And this means that the respective areas of effective mutual influence must be much larger than that in crystals, implying that such a large area (possessing a certain symmetry) cannot be the result of simple chemical forces of the motifs. Such areas involve large distances, way beyond those involved in ordinary chemical reactions. The motifs in the organic lattice, ex hypothesi, 'know' about the presence of their direct neighbors (i.e. the other motifs of the lattice in the immediate vicinity or even beyond). How they 'know' we cannot say. All we can say is that even in crystals we also have to do with such 'long-range information transfer' as we saw it in (branched) snow crystals. It is part of the (holistic) organization of the living system.
Like in the case of crystals, these large areas of effective mutual influence, as they are in organisms, will pack together (while overlap results in repulsion of the motifs) resulting spontaneously in one or another (organic) lattice of which the internal symmetry (i.e. the total symmetry, including translational elements), and thus the lattice type, depends on the point symmetry of these areas (which are now the motifs of the lattice), and the shape and structure of the basic building block consisting of a definite number of these areas, each one of which contains a chemical motif.
Saying that the (chemical) motifs are closely packed together, means that their areas of effective mutual influence are contiguous, i.e. these areas are in direct contact with their nearest neighbors ( Thus we cannot say that these areas attract or repel each other. Only their corresponding chemical motifs attract or repel each other).
This is an important result : we can say that the organic lattice emerges s p o n t a n e o u s l y without presupposing any pre-existent vectorial medium, or in other words, the anisotropic state, represented by the organic lattice, can be generated by, and in, an isotropic medium, which process is an example of symmetry-breaking. The pointsymmetrical d e t a i l e d structure -- as we see it (also) in snow crystals or in windowpane frost -- resulting from the non-equilibrium crystallization of the (one) material of the organic lattice, functions as (and only as) the g l o b a l l o c a l i z a t i o n m e d i u m of the given developing organism. It is its global vectorial framework (and no more than that).
And the organism is assumed to compensate for all the effects of chemical agents not belonging to the lattice, i.e. it isolates this lattice chemically.
And this isolation is assumed to be driven so far that even topological deformations of the lattice are also compensated for, i.e. all information about the symmetry of the lattice is preserved under these deformations. The wide separation of the motifs in an organic lattice also prevents the organism to become a solid mass : it preserves the semi-liquid state of the organism.
And this, finally, is what we meant by saying (earlier) that such a lattice, such an organic lattice, is an "e l e v a t e d l a t t i c e" , elevated with respect to a lattice of an ordinary crystal, or, in other words, that it is not identical with, but only analogous to such a crystal lattice.
And, as we've said, also many other properties of crystals reappear as the corresponding 'elevated properties' in organisms, as is evident from the many crystal analogies.
Deformation of an organic lattice.
We just spoke about the possible topological deformation of an organic lattice and the preservation (under such a deformation) of the information content inherent in such a lattice.
Because the embryo of a developing organism can move, in the sense that it can adopt different postures (it can bend and stretch itself, and is often in a more or less folded position), the (organic) lattice must follow these postures. This means, for example, that mirror planes can become curved surfaces, and translations curved lines. But, fully in the context of the embryo itself, nothing is assumed to change, whatever movements and changes in posture the embryo is carrying out. So the lattice bends together with the embryo. The next diagrams explain things for geometrically simple cases.
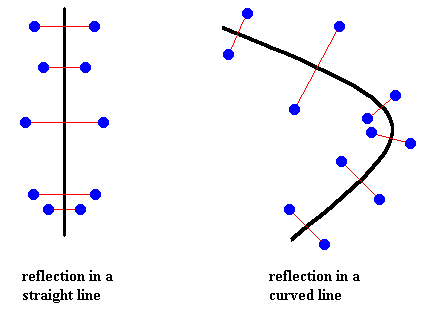
Figure above : Reflection in a straight line, and reflection in a curved line.
Although the figure (pattern of dots) of the right image is in fact not reflectionally symmetric, it is so symmetric when we ignore the curving of the line, i.e. when we follow this line and forget about all that went before on this journey along that line. So the successive reflections are then in fact reflections in successive points of the line.
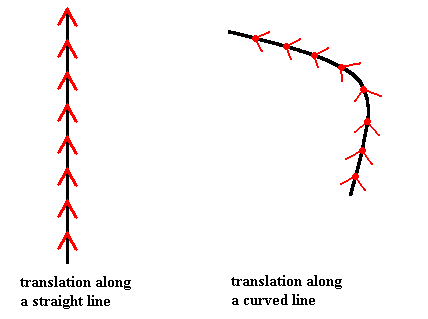
Figure above : Translation along a straight path and translation along a curved path.
A translation is, by definition, a displacement of a certain magnitude along some straight line.
In the right-hand image it is a curved translation, which therefore contradicts the definition of translation. But if the curved line is taken all by itself, as a one-dimensional space, i.e. when the two-dimensional space in which it is embedded, is not taken into account, the line can be taken as straight.
In both cases the figure (when thought to extend indefinitely) will be superimposed upon itself when translated according to the translation as given by the arrow, which means that each figure is translationally symmetric (and when we imagine identical features to be present at the tip of each arrow, then it is symmetric in virtue of this particular translation (as indicated by the length of the arrow) only).
The case of rotational symmetry in the context of a distorted or deformed lattice goes as follows : Generally, like in the above cases, we must, when we perform symmetry transformations on a folded lattice, follow the distortions. If the symmetry transformation, for example, a two-fold rotation (half-turn) of a distorted lattice, would look like the right-hand image in the next Figure (i.e. if this image is supposed to be 2-fold rotational symmetric), then a is transformed into b while it gradually deforms, and b is transformed into a while it also gradually deforms. The deformations that take place during the half-turn are supposed to be such that the appearance and orientation of the whole structure remains the same, which means that this structure indeed possesses a two-fold rotation axis, i.e. the structure is 2-fold rotationally symmetric. See next Figure.
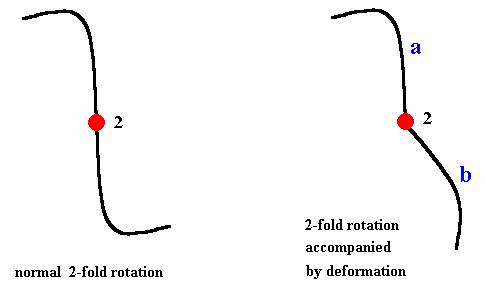
When the embryo bends and the lattice bends with it, the assumed nature of this latice implies that all its symmetries remain exactly the same. The deformation is just topological in nature, which means that no tears (breaks) and the like are involved. So even when the embryo, or a stadium in metamorphosis initiating a different symmetry (like in Echinoderms), is temporarily folded in complex ways, the lattice is folded with it. This can, in metamorphosis, either be still the old lattice, or already the new lattice into which the former transforms (Echinoderms).
The next two Figures illustrate what is meant by a topological transformation and which is assumed to be the case when foldings and the like occur in developing organisms resulting in the deformation of their organic lattice. The images are taken from D'ARCY THOMPSON, 1942, actually from a reprinted but abridged edtion (1975) of his On Growth and Form. There such images were supposed to show topological form-relationships between organic structures. In fact they represent the first (because they were already published in 1917) field theory in biology.
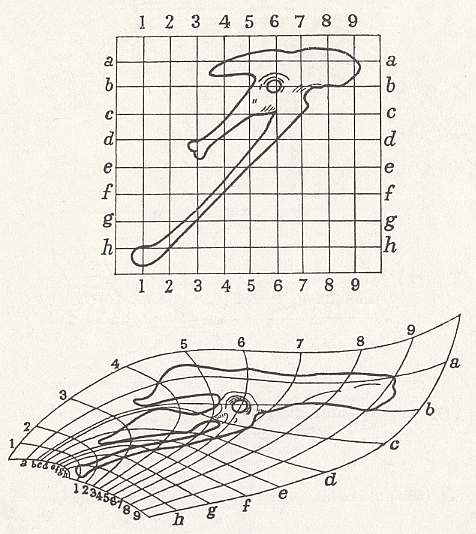
Figure above :
Top image : Pelvis of Archaeopteryx (primitive reptile-like bird, having lived in Jurassic times). Square coordinate grid.
Bottom image : Pelvis of Apatornis. Deformed coordinate grid.
(After D'ARCY THOMPSON, (1917, 1942), 1975.)
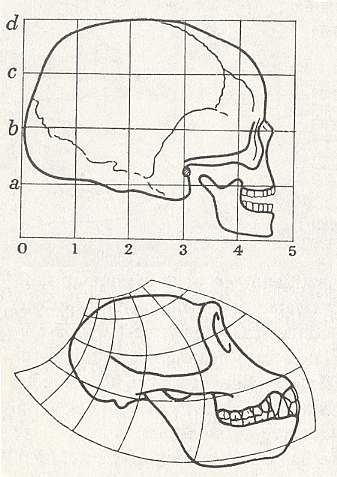
Figure above :
Top image : Human skull. Square coordinate grid.
Bottom image : Skull of chimpanzee. Deformed coordinate grid.
(After D'ARCY THOMPSON, (1917, 1942), 1975.)
It is in this way, i.e. like in the above Figures, that we must imagine the folding and deformation of the organic lattice.
The status of recent research on deciphering the structure of (inorganic) quasi-crystals is such that one is not (yet) able to observe this structure directly, let alone that one could observe an organic (quasi) lattice in the background of a developing embryo, where this lattice is, in addition to being folded in some cases, internally mixed up with other chemical entities, destroying any clear-cut anisotropy. So, to date (end of 20th century), the argument of ' hasn't been observed ' cannot be brought up against our hypothesis.
Spatial structure resulting from cell division?
When we postulate an organic (diluted) lattice or quasi-lattice (as in quasi-crystals) to provide for point symmetry and localization, after the fashion of a snow crystal, we must somehow be convinced first that such a system is necessary at all (for most organisms), and, secondly, that it must be a lattice. That it is reasonable that it is a lattice, is clear, because a lattice or quasi-lattice is more or less the same everywhere (within the region where it is present), so no differential and patterned distribution of molecules or other structures need be presupposed. That there must be a localization medium at all, is more or less evident to me, because I can think of no other way to provide for the vectoriality (regular spatial distribution of parts) of the organismic body.
But one could think that cell division during embryological development could, all by itself, do the job of providing the organic body with vectoriality. The unfolding pattern of successive (and simultaneous) cell division could generate the global symmetry of the resulting organism, without the need for any pre-existing (pre-generated) localization system with its inherent symmetry.
Although I am not an embryologist, I think I can come up with at least two objections against this idea, i.e. that cell division alone would be able to generate the organism's overall vectoriality.
First of all there are unicellular organisms with a very regular and determined internal and external geometry of their body (without being just drop-like forms), for example all Acantharia, and many other Radiolarians, further, many Diatomeans and Dinoflagellates ( The latter being asymmetric, but nonetheless having a robust and (therefore) constant, and definite structure). These forms, structures and symmetries are not the result of (repeated) cell division, because these organisms do not develop and grow by (repeated) cell division.
Secondly, cell division would not be a robust generator of global structure and symmetry, because one or a few divisions taking place in the wrong or in a deviating direction (i.e. the direction of the plane of partition of a cell) can be expected to have a large effect on the resulting global structure and symmetry.
So indeed no local determinants of global structure and symmetry, like genetically programmed cell division angles, can do the job (even apart from the fact that angle determination needs some reference direction in order to be possible). Our postulated organic (quasi) lattice is a global determinant of structure and point symmetry.
In the early stages of individual development any of the new-born cells (as a result of cell division) can divide, and produce, when isolated, an entire organism. Such a cell is said to be totipotent (like a crystal : any fragment of it -- above a certain size -- can grow into a macroscopic crystal again). Later in that individual development, however, although all the genes are still present in all the cells, which genes are active (i.e. expressed) depends on the developmental history of the given cell : that is, on how many times the cell line, that leads to it has divided (constituting the temporal aspect of that cell), and whereabouts in the developing embryo that cell is located. So gene expression -- resulting in the emergence of qualitatively different cell groups -- depends on both time and space (See ROSE, S., Lifelines , 1997, p.110). And whereas the number of times of cell division could be recorded somewhere in the cell by scalar means, its location within the embryo cannot, I think, be assessed (by the cell) by scalar means, but by a set of vectors along the lines of some (pre-generated) lattice, with respect to a chosen point, which could be the center of the point symmetric 'crystal' resulting from that lattice.
Cell migration.
The cells in a developing embryo do not only divide, but can also migrate to certain specific locations within the embryo. How do these cells find their final destination?
If we think of our organic lattice as some 'crystalline' entity that grows (like a crystal), and take into account controlled fast growth, i.e. controlled non-equilibrium crystallization, then we expect a complicated and detailed pattern to emerge, as we see it in many snow crystals. The fine details of such an 'organic snow crystal' are first of all expected to consist of a series of grooves and ridges, lacily patterned across the crystal, i.e. we expect these details to be morphological surface features. It is, however, reasonable to expect, in addition to these (macroscopic) surface features, also the emergence of small, but macroscopic, channels, pervading the structure (i.e. pervading the (quasi-)crystalline structure of the material that forms the lattice). If this is correct, then our organic lattice, in the form of a pointsymmetric and detailed structure, even better serves the function of being an underlying global morphological and vectorial framework setting the stage for the development of the organism. It especially sets the stage for migrating cells, or the growing of axons (which are long extensions of nerve cells (neurons)), traveling to specific destinies within the embryo. With respect to all this it is instructive to quote ROSE, S., Lifelines , 1997, p.148--152, where he discusses cel migration (and axon growth) during the development of the nervous system in humans :
In the developing brain it is the glial cells that begin the migratory pattern. As they move away from their sites of origin and towards what will become the cortex, they spin out long tails, up which the neurons can in due course climb. As Edelman and others have shown, the cell membranes of both neurons and glia contain a particular class of proteins called cell adhesion molecules (CAMs). In the developing tissue the CAM molecules work rather like crampons : they stick out from the surface of the membrane and cling to the matching CAM on a nearby cell. The neurons are thus able to clutch the glia and ratchet themselves along their tails. As a further trick, the migrating cells also lay down a sort of slime trail of molecules related to the CAMs -- substrate adhesion molecules (SAMs) -- which provide additional guidance for the cells following along behind.As we saw, "One way of signalling [one or another] direction is to have already in place some target cell or tissue towards which the migration can be directed."
But what provides the map references for such cellular route marches? Both distant and local signals must be involved. One way of signalling direction is to have already in place some target cell or tissue towards which the migration can be directed. Suppose the target is constantly secreting a signalling molecule, which then diffuses away from it. This will create a concentration gradient, highest at the target and progressively weaker at increasing distances. If the migrating cell can sense the signalling molecule and move towards it, rather as bacteria can swim towards sources of food, then it will eventually arrive at the target. In the 1950s Rita Levi Montalcini identified one such signalling (or trophic) molecule, which she called nerve growth factor. By the time she was awarded her Nobel prize for the discovery, in 1986, it had been recognized as but one of a growing family of such molecules.
Trophic factors can provide the long-range guidance which enables the growing axons of motor nerves to reach out and find their target muscles, or the axons from the retinal neurons which form the optic nerve to track their way to their first staging post within the brain, the lateral geniculate. However, the migrating cells or growing axons also need to keep in step with one another -- each has to know who its neighbours are. The diffusion of a local gradient molecule, together with the presence of some types of chemosensor on the axon surface, could enable each to determine whether it has neigbours to its right and left and to maintain step with them. The entire troop of axons would then arrive in formation at the lateral geniculate and make appropriate synaptic connections, thus creating in the geniculate a map -- albeit a topographically transformed one -- of the retina, rather like the relationship between the London Underground or New York subway system and the maps of them on display at stations. Indeed, the brain holds many such maps, multiple maps for each of its input sensory systems and output motor systems, maps whose topology must be preserved during development.
The process just described would be compatible with an instructionist model. Each axon is kept on course by instructions from its environment, both the trophic factor diffusing from the target region and the relationships with its nearest neighbours directing it to its final site. There is some evidence that a considerable part of the nervous system's development can be accounted for in such a model. However, Edelman drew attention to another vital feature of development. During embryonic development there is a vast overproduction of cells : many more neurons are born than subsequently survive. Since more axons arrive at their destination than there are target cells to receive them, they must, argues Edelman, compete for targets. Those that do not find them wither away and die. The argument actually goes further : it is not only neurons and their axons which are overproduced, but the synapses too. There is a superabundance of synaptic production, a veritable efflorescence. But if synapses cannot make the appropriate functional connections with the dendrites of the neurons they approach, they too become pruned away and disappear. In this model of development, because there is competition for scarce resources -- trophic factor, target cell, synaptic space -- there is also selection. And now we have only to imagine that it is in some way the ' fittest ' of the neurons and synapses that win out in the competition, and we arrive at Edelman's 'neural Darwinism'.
Selection in this sense can account for local but not distant processes. Long-range order, the migration of cells and the growth of axons over long distances, would seem to require something more -- the execution of some internal programmes of both individual cells and the collectivity of cells acting in concert. Even though synapses from only a particular neuron may end up making successful connections with its target cell, if the others had not been present during the long period of growth and migration it is doubtful whether a single nerve axon would have been able even to reach the target. The survival of one depends on the presence of the many. Overproduction and subsequent pruning of neurons and synapses may at one level of magnification look like competition and selection. Viewed on the larger scale, they appear as cooperative processes.
Vectorial (directional) and scalar (numerical) regularity in unicellular organisms : Acantharia (Radiolaria).
In the above we discussed pattern formation by cell division (and in many cases followed by cell differentiation), and cell migration, and we saw that still some sort of pre-generated vectoriality must be assumed. And this is even more so when we consider unicellular organisms, especially those that are not simply drop-like (whose form can possibly be explained by surface tension phenomena), but have a regular form of anisotropy, resulting in certain constant directions being pronounced with respect to other directions. This we see very clearly in the case of the Acantharia which is a group of Radiolarians ( The latter are unicellular but complex planktonic marine organisms (smaller than 1mm), in most cases possessing a skeleton (mineral or otherwise), wich often is very regular and consists of perforated concentric spheres and/or radially placed needles).
The skeleton of the Acantharia is made from strontium sulfate (SrSO4) and consists of 20 needles (often provided with outgrowths) that are arranged according to 'Müller's Law' : If we imagine these needles as originating from the center of a sphere (such as the earth), then there are four arctic polar needles (going through the arctic circle), four northern tropic needles (going through the northern tropic), four equatorial needles (going through the equator), four southern tropic needles (going through the southern tropic) and, finally, four antarctic polar needles (going through the antarctic circle). See next Figure.
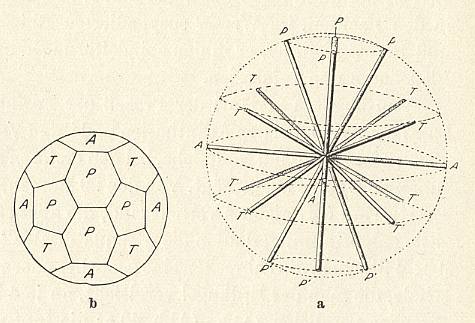
Figure above : 20-fold system of the mineral skeleton of Acantharia (Radiolaria).
a (right image) : Lateral view (i.e. a view perpendicular to the axis that connects the poles) of the ordering of the 20 needles.
b (left image) : Polar view of the areas geometrically connected with the pattern of the needles as they stick out of the imaginary sphere from whose center the needles originate.
A = equatorial needles, T = tropic needles, P = polar needles.
(In WOLTERECK, R., Grundzüge einer allgemeinen Biologie, 1932. After KÜHN, 1926.)
The next Figures show some Acantharia and their clear vectoriality.
Figure above : Polar view of Xiphacantha (Acantharia, Radiolaria).
Whole cell with multi-nuclear central capsule and two strenghened equatorial needles ( The other needles being weaker developed).
(In WOLTERECK, R., Grundzüge einer allgemeinen Biologie, 1932. From KÜHN, 1926.)
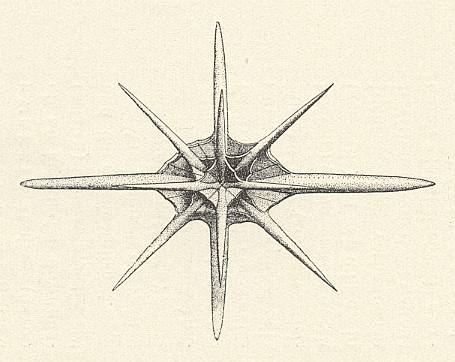
Figure above : Polar view of Phyllostaurus (Acantharia, Radiolaria). Skeleton only.
(In WOLTERECK, R., Grundzüge einer allgemeinen Biologie, 1932. From KÜHN, 1926.)
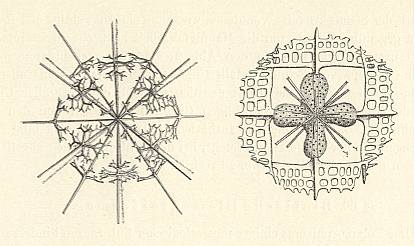
Figure above : Two more examples of Acantharia (Radiolaria).
Left image : Skeleton only. In the right image we see, in addition to the skeleton, a four-fold central capsule. The equatorial needles have developed outgrowths ('wings').
(In WOLTERECK, R., Grundzüge einer allgemeinen Biologie, 1932. From HAECKEL, a.o.)
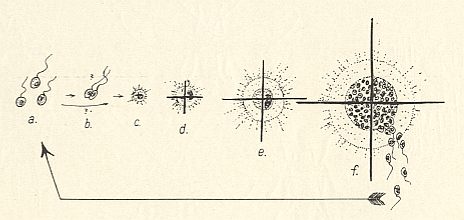
Figure above : Developmental cycle of an Acantharian (Radiolaria).
a Spores, c--f Acantharian with definite radii (as in the next Figure), nucleus and central capsule. In f formation of spores.
(After WOLTERECK, R., Grundzüge einer allgemeinen Biologie, 1932.)
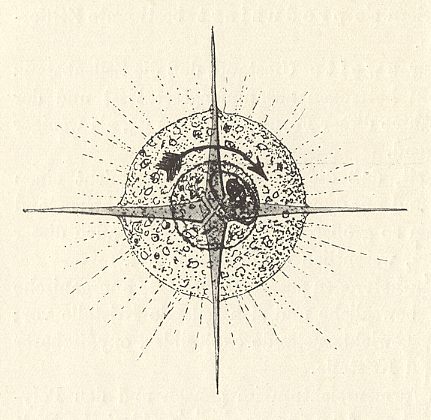
Figure above : System of a young radiolarian cell (Acantharian with four equatorial radii, the other radii omitted. The cell protoplasm is constantly in motion (according to WOLTERECK, 1932) : radially, as well as tangentially (circularly, indicated by the arrow). The dashed lines indicate the pseudopodia that radiate from the body ( They are protoplasmic threads and serve to apprehend food particles).
(After WOLTERECK, R., Grundzüge einer allgemeinen Biologie, 1932.)
Let us discuss some features of radiolarian skeletons in general, and more specifically of the Acantharia.
. . . a great part of the body of the radiolarian, and especially that outer portion to which Haeckel has given the name of the 'calymma', is built up of a mass of 'vesicles', forming a sort of stiff froth, and equivalent in the physical though not necessarily in the biological sense to 'cells', inasmuch as the little vesicles have their own well-defined boundaries, and their own surface phenomena.These vesicles with their boundary walls or films, but especially with their edges and their corners, provide the system and distribution of surface energy, as a condition for adsorption of certain materials that could give rise to, or is at least some pre-existing scaffolding for, the radiolarian's skeleton.
In many cases it is the arrangement of the axial rods -- the 'polar symmetry' of the entire organism [i.e. its promorph] -- which lies at the root of the matter, and which, if only we could account for it, would make it comparatively easy to explain the superficial configuration [of, say, Acantharia and some Phaeodaria]. But there are no obvious mechanical forces by which we can so explain this peculiar polarity [meaning that this polarity cannot -- as it seems -- be explained by a theory of vesicles and their surface tension phenomena]. This at least is evident, that it arises in the central mass of the protoplasm, which is the essential living portion of the organism as distinguished from that frothy peripheral mass whose structure has helped us to explain so many phenomena of the superficial or external skeleton. To say that the arrangement depends upon a specific polarisation [promorph] of the cell is merely to refer the problem to other terms, and to set it aside for future solution.Maybe the postulation of a spontaneously pre-generated lattice or quasi lattice, perhaps based on average positions, and grown into a radiate structure as a result of a controlled non-equilibrium crystallization, could present some beginnings for such an explanation.
The above mentioned 'polar symmetry' or promorph (stereometric basic form) of the Acantharia (Radiolaria) is either (i.e. in some acantharia) belonging to the (Stauraxonia homopola) Isostaura octopleura (regular bipyramids with eight sides), see next Figure,
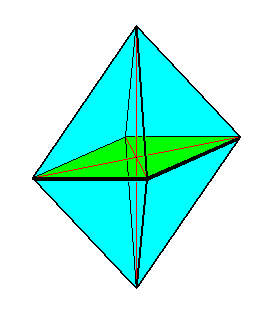
as it is the case for all four-fold Acantharia (See the one that was depicted above (right image) ).
or (the promorph of the Acantharia is) belonging to the (Stauraxonia homopola) Allostaura octopleura (amphitect bipyramids with eight sides), see next Figure,
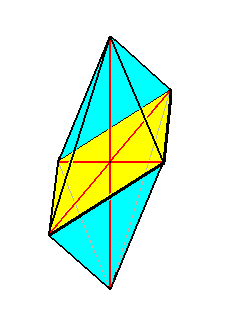
Figure above : The eight-sided amphitect bipyramid (Rhombic Octahedron) as the basic form of the Allostaura octopleura. The equatorial plane is emphasized (yellow), it is a rhombus. The ideal cross axes (Euthini) are contained in the equatorial plane.
as is the case for all two-fold Acantharia (See the one that was depicted above ).
As has been said, the mineral part of the skeleton of the Acantharia is strontium sulfate, and it is interesting to note that the crystallography of this substance is as follows : Rhombic-Dipyramidal Class (2/m 2/m 2/m) of the Orthorhombic Crystal System. The general Form of this Class is the orthorhombic dipyramid or, equivalently, rhombic octahedron, which is the basic form (in the promorphological sense) of the above mentioned Allostaura octopleura.
We will now try to explain the structure of a simple four-fold acantharian (Radiolaria) in terms of the system "Tetragonal Lattice + Fast (unstable) Growth" , i.e. in terms of its morphological lay-out being generated by non-equilibrium crystallization of a crystal, in the present case supposed to belong to the Ditetragonal-Dipyramidal Class (4/m 2/m 2/m) of the Tetragonal Crystal System, and chemically consisting of the material of the organic lattice (which is not the material of the skeleton, strontium sulfate, which crystallizes in the Orthorhombic Crystal System rather than in the Tetragonal Crystal System). See next Figures.
REMARK : We must stress that the following explanation of the morphology of four-fold acantharia is not meant to represent a methodology. It is only meant to obtain a better and more concrete idea of an organic lattice.
Figure above : Delineation of some possible crystal faces in a tetragonal lattice. This lattice consists of the periodic stacking of tetragonal building blocks. The latter are quadratic prisms, i.e. parallelepipeda with four vertical rectangular faces making angles with each other of 900, and one quadratic horizontal top face and one quadratic horizontal bottom face. In the figure we look in the direction perpendicular to a vertical prism face, so we see a system of periodically stacked rectangles. Possible faces are either along the edges of the building block or stepwise along the building blocks. Each such face involves one whole-number step in vertical or horizontal direction.
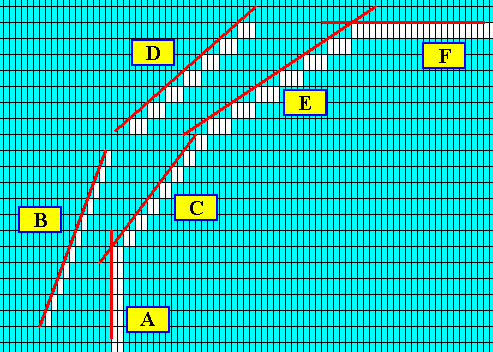
Figure above : The possible faces (as a selection of a larger set of possible faces) are highligted by red lines and marked by letters.
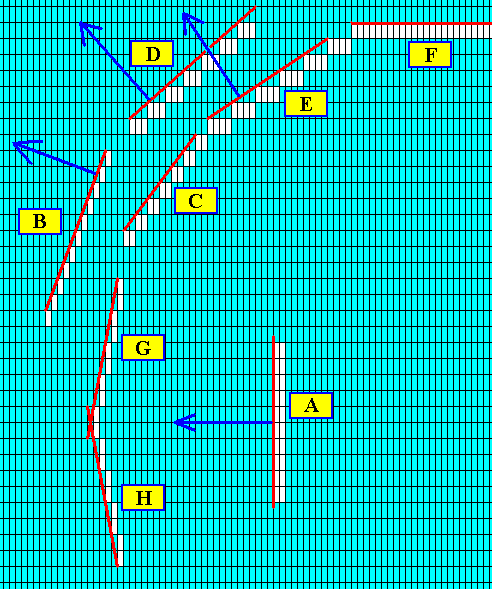
Figure above : Two more possible faces are added : G and H. The direction of growth of the faces B, D, E and A is indicated by blue arrows ( The growth direction -- growth vector -- of a given crystal face is always perpendicular to that face).
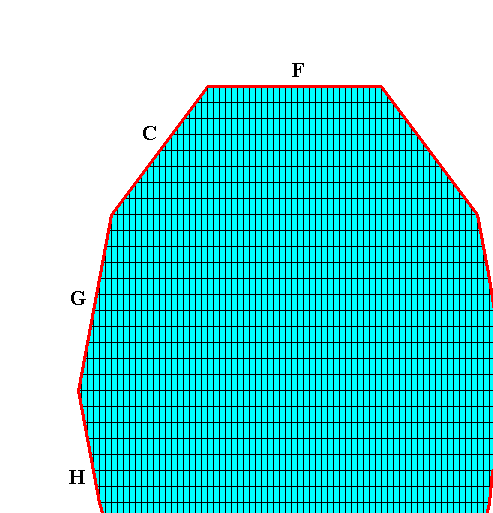
Figure above : The crystal (part of it displayed) as consisting of the faces H, G, C and F (and their symmetrical counterparts). These faces are supposed to be the slowest growing faces, and it is these faces that finally appear and remain in the crystal. The possible faces E, B and A (and also all other posible faces) are supposed to grow faster than their adjacent faces and thus (because the latter taper) grow themselves out of existence. Their growth directions are indicated in the next Figure.
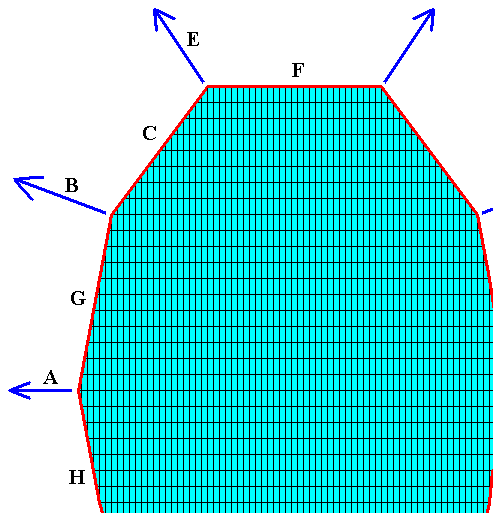
Figure above : The growth directions of the faces E, B and A are indicated by blue arrows. They are possible faces that have disappeared because of their fast growth with respect to the faces that lie next to them.
When, after a small initial crystal -- as depicted here -- has been developed (during a short interval of equilibrium crystallization), non-equilibrium crystallization sets in, outgrowths will start off from the corners of the crystal (because they stick out into the nutrient environment) and grow in the direction of the fast growing faces E, B and A, etc. (and thus grow in the directions of the arrows).
In the above Figure we have presented a crystal bounded by a set of possible faces (that are supposed to be the slower growing faces), and have indicated the directions of some of the fast-growing faces. These latter directions can represent the beginnings of outgrowths (branches) from the crystal's corners when non-equilibrium crystallization sets in.
We can now interpret all this in terms of an organic lattice, the material of which crystallized in a crystal, which is sized in a special way, namely such that the selected fast-growth directions (corresponding to the possible faces A, B and E) converge in one point that lies in the center of the crystal. See next Figure.
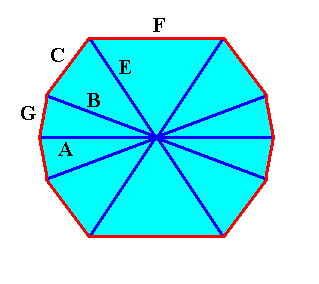
Figure above : Projection, in the direction of one of the (two) subsidiary crystallographic axes (a2) ( These subsidiary axes lie in the equatorial plane of the crystal), of a Tetragonal crystal (i.e. a crystal belonging to the Tetragonal Crystal System) enclosed by the faces G, C, F, and their symmetrical counterparts, and implying the directions of fast growth corresponding to the possible faces A, B and E and their symmetrical counterparts, while these directions converge in the center of the crystal. The equatorial plane of the crystal (containing the a1 and a2 crystallographic axes) is seen as a horizontal line in the Figure. The crystal's c-axis is perpendicular to the equatorial plane.
The direction A and its symmetrical counterparts (lying in the equatorial plane) correspond to the equatorial needles, the direction B and its symmetrical counterparts correpond to the tropic needles, and the direction E and its symmetrical counterparts correspond to the polar needles of a four-fold acantharian (Radiolaria). See next Figure.
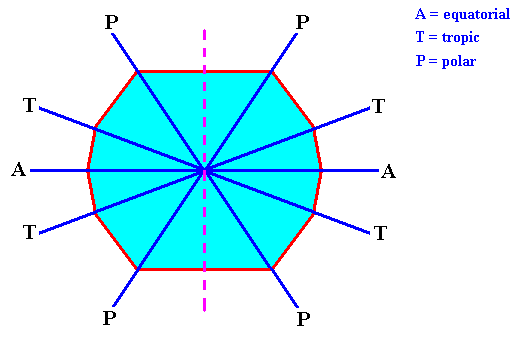
Figure above : The fast-growing directions become the needles (equatorial [A], tropic [T] and polar [P] ) of the acantharian seen in projection along one of the subsidiary crystallographic axes (a2). For these axes see next Figure. The dashed line indicates the acantharian's main body axis (which has not been materialized into a needle).
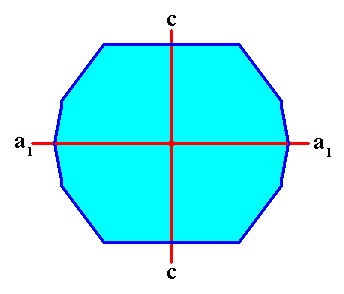
Figure above : In the above Tetragonal crystal two (of the three) crystallographic axes, c and a1 , are indicated (red lines). The third axis, a2 , originates in the point of intersection of c and a1 , and is perpendicular to the plane of the drawing. The axes a1 and a2 are equivalent, they are of equal length.
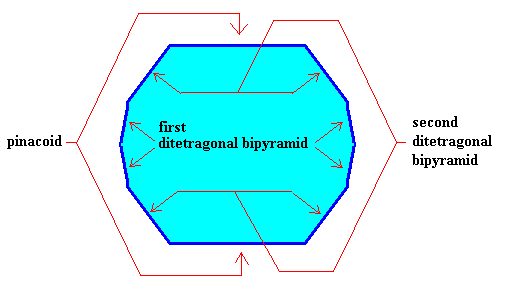
Figure above : The above crystal is supposed to belong to the Ditetragonal-Dipyramidal Class (4/m 2/m 2/m) of the Tetragonal Crystal System.
In the present case it is supposed to be a (crystallographic) combination of three crystallographic Forms, viz., one pinacoid (consisting of two parallel horizontal faces, capping the crystal's top and bottom ends), one first ditetragonal bipyramid and one second ditetragonal bipyramid. A ditetragonal bipyramid (as one of the crystallographic Forms of the present Crystal Class) consists of two congruent pyramids, in our case connected base to base. And this base has the shape of a ditetragon, i.e. an octagon with alternately equal angles. So a ditetragonal bipyramid is a Form (of the present Crystal Class) consisting of 2 x (2 x 4) = 16 (crystallographically equivalent) faces. There are several such bipyramids possible, differing by the inclination of the sides (resulting in squat or slender bipyramids). In the present case we have two such bipyramids.
If we look to this crystal, not along the a2 axis (as in the above Figures), but along the c axis, then we see the ditetragonal outline of the crystal, allowing for the tropic needles to be possible ( The tropic needles of any acantharian lie in different meridian planes than the equatorial and polar needles do). See next Figures.
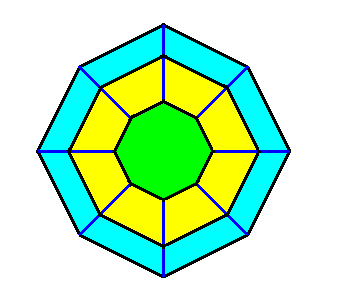
Figure above : View of the above Tetragonal crystal (i.e. belonging to the Tetragonal Crystal System) along the c-axis . We see one of the two faces of the pinacoid (green), the upper part of the first ditetragonal bipyramid (blue), and the upper part of the second ditetragonal bipyramid (yellow). The equatorial plane of the crystal is a ditetragon.
The relative magnitudes (sizes, extensions) of the areas representing the faces of the crystal are not the same in this and the above Figures, but are supposed to be the same.
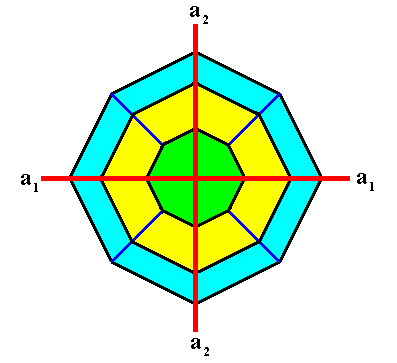
Figure above : Again, view of the above Tetragonal crystal along the c-axis .
Two crystallographic axes, a1 and a2 , are indicated (red lines). The third crystallographic axis, the c-axis, originates in the point of intersection of the a1 and a2 axes, and is perpendicular to the plane of the drawing.
The ditetragonal outline of the above crystal (as viewed down the c-axis) allows for directions of fast-growing possible faces, corresponding to the directions of the needles of a four-fold acantharian. See next Figure.
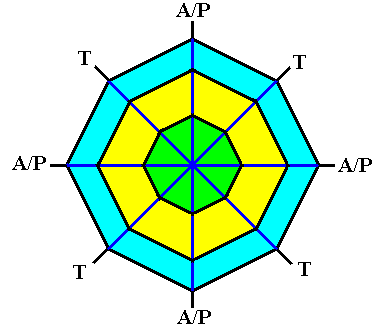
Figure above : The ditetragonal shape of the (initial) crystal creates corners that can intiate branches (outgrowths) when non-equilibrium crystallization sets in. The directions of the outgrowths that actually form, correspond to the needles of a four-fold acantharian.
A/P = direction of equatorial and polar needles.
T = direction of tropic needles.
In the case of the polar and tropic needles we in fact have to do with only one component of their actual direction, namely the component that lies within the equatorial plane.
In earlier Figures we have drawn the crystal as being built up by tetragonal building blocks (rectangles in the Figures) and viewed along the a2 axis. Now we will draw this crystal -- and its being built up by tetragonal building blocks -- as seen down along the c-axis. The building blocks will then appear as squares. See next Figures (Also these are not drawn on the same scale and also not with the same relative extension of faces as in earlier Figures. But of course these Figures are still comparable with respect to the items under discussion).
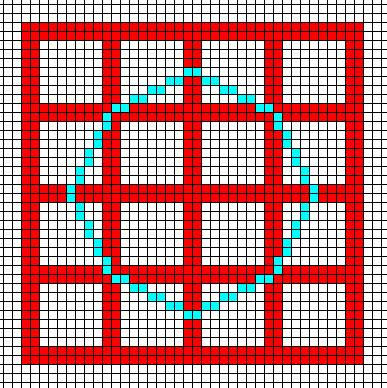
Figure above : Construction of the ditetragonal outline (blue) of the crystal under discussion. This outline of the crystal, as seen along its c-axis, represents eight equivalent possible faces (possible in a tetragonal lattice). See further, the next Figures.


Figure above : The material of the crystal (as seen down along its c-axis) is filled in (blue). Each building block consists of a definite number and arrangement of chemical motifs (not shown).
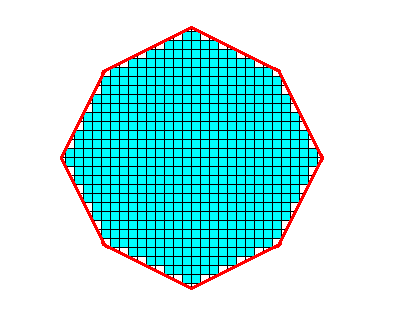
Figure above : The crystal and its lattice.
As such the crystal is constituted by the periodic stacking of tetragonal building blocks. These building blocks appear (because they are viewed down along the c-axis) as squares. The equatorial edges of the crystal are highlighted by red lines, clearly showing the ditetragonal outline. In fact these edges represent the possible prism faces of the crystal. These faces are, however, supposed to grow fast, resulting in their disappearance in the course of the crystal's normal growth. The equatorial edges are common to both the prism faces and the faces of the first ditetragonal bipyramid.
The next Figures indicate the outline of the first ditetragonal bipyramid, of the second ditetragonal bipyramid, and of the pinacoid. These three Forms together constitute our crystal, i.e. the crystal is a combination of these three (crystallographic) Forms.
Figure above : Outline of the basal edges of the first and second ditetragonal bipyramids and of the pinacoid. Here we see only the upper parts of these (crystallographic) Forms. Each edge is common to two possible crystal faces.
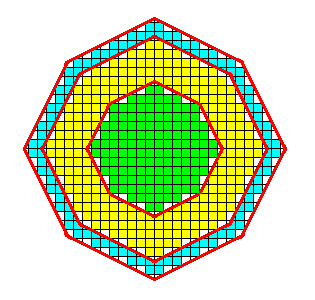
Figure above : The three Forms are highlighted by coloring : First ditetragonal bipyramid, blue. Second ditetragonal bipyramid, yellow. Pinacoid, green.
Figure above : The (visible) faces of the three Forms (first and second ditetragonal bipyramid, pinacoid) are indicated. (See also the Figure given earlier ). As has been said, I did not make any effort to draw this Figure with the same face extensions as in the corresponding Figures given earlier (which is immaterial for the present argument).
We can now insert into the diagram of the crystal of the above Figure the (directions of the) needles of a four-fold acantharian. See next Figure.
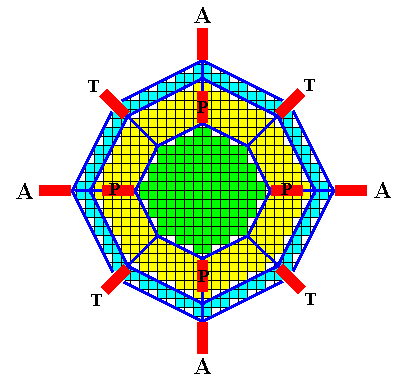
Figure above : Possible directions of the needles of a four-fold acantharian on the basis of the crystal, the lattice of which is the organic lattice of that acantharian.
All twenty needles originate in the center. Twelve of them are visible in the drawing (indicated by red bars) :
A = equatorial needle. T = tropic needle. P = polar needle.
The (directions of the) needles are shown as they appear when the crystal/acantharian is viewed down along the c-axis. The tropic and polar needles are in fact inclined with respect to the plane of the diagram. We must imagine that the initial polyhedral crystal is the result of slow growth (equilibrium crystallization), followed by controlled fast unstable growth (non-equilibrium crystallization), resulting in branches going off from the (initial) crystal in the directions indicated. So the lattice is actually only present in the initial crystal and in its branches.
The fact that not all corners of the initial polyhedral crystal give off branches is supposed to be the result of controlled non-equilibrium crystallization. Such a controlled (non-equilibrium) crystallization cannot be expected to happen in real crystals, but is assumed to be possible for crystal growth of organic lattices.
It is possible that on the branches secondary branches are given off, and that between the main branch and such a secondary branch a slow-growing crystal fase develops (like we can see it in snow crystals). See next Figures, where we have provided the equatorial branches (equatorial needles) with such secondary branches and developed faces.
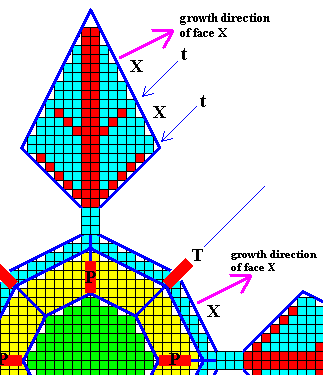
Figure above : Outgrowths (secondary branches) given off from the equatorial branches of the crystal of the previous Figure.
We can see the face X of the main crystal being repeated in the equatorial outgrowths (Recall that a crystal face is totally defined by its direction, and that its direction of growth is perpendicular to it). The growth direction of face X is indicated by purple arrows.
The secondary branches (t, red), going off from the main branch (red), are indicated. They have grown in the same direction (as projected onto the equatorial plane) as that of the tropic outgrowths (T), and they represent (together with T) the direction of fast growing possible faces of the crystal.
Between these secondary branches and the main branch the face X grows outward.
The complete crystal, including its four equatorial outgrowths, can be seen, either in an enforced screen-fitting overview (if browser supports this) by clicking HERE (to return, close window), or just as the whole crystal (without diminution), by clicking HERE (to return, close window).
The growth pattern just given for an organic lattice is exemplified in snow crystals, as can be seen in the image given in Part XXIX Sequel-8 and also in the next Figure.

Figure above : Development of so-called sectored plates in a snow crystal : slow-growing faces (which also represent the sides of the central hexagon) are developed between side-branches.
(After LIBBRECHT, The Snowflake, 2003.)
(Photography by Patricia Rasmussen)
Of course it is also possible that in a single (main) outgrowth two faces of the central hexagon are developed. See next Figure.
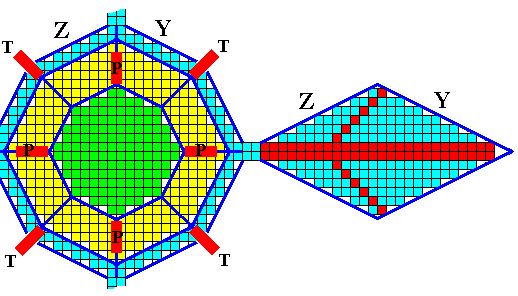
Figure above : In this particular example the faces Y and Z are also developed on the corresponding main outgrowth. The same, mutatis mutandis, is then the case for the remaining five main outgrowths.
For another realization in snow crystals of such plate-like outgrowths see image given in Part XXIX Sequel-8
This concludes our consideration concerning the organic lattice as it could be present in four-fold acantharians (Radiolaria). Again, it is important not to confuse the 'organic crystal' with the actual mineral skeleton of the organism. The organic crystal (or paracrystal, we might say), having resulted from controlled non-equilibrium crystallization of the material of the organic lattice, forms only a morphological matrix (morphological lay-out) of the given organism, and as such plays a directive role in the morphogenesis of certain parts of that organism.
General remarks on organic lattices.
As has been said, according to the theory of organic lattices, the organism is not a crystal (also not a branched crystal). The paracrystalline entity, which we have called a growing organic lattice, is only some underlying form matrix of the organism, onto which actual structures are laid down or through its channels and grooves cells and chemicals migrate.
In itself such a matrix, such a soft 'crystal' (i.e. a crystal that has imbibed one or another liquid, say, water, resulting in a more or less swollen or inflated crystal), is a holistic system (as we saw it [also] in snow crystals) integrated in the larger system, which is the organism as a whole. Perhaps the organic lattice, while being itself a whole, imparts its property of wholeness to the entire organism.
Such a whole is a genuine structure. In defining something to be a structure, it is instructive to quote HARAWAY, D., Crystals, Fabrics, and Fields, Metaphors of Organicism in Twentieth-Century Developmental Biology, 1976, p.61 (where she in turn quotes the Swiss psychologist Jean Piaget, 1971). Comments of mine between square brackets.
A structure "is a system of transformations [for example symmetry transformations]. Inasmuch as it is a system and not a mere collection of elements and their properties, these transformations involve laws : the structure is preserved or enriched by the interplay of its transformation laws . . . In short, the notion of structure is comprised of three key ideas : the idea of wholeness, the idea of transformation, and the idea of self-regulation" [italics added by HARAWAY].It is of course hard to define the "properties of its elements", because they could include those (properties) that express the element's behavior within a system of which it is an element.
The question of form is central to [philosophical] structuralism. Shape is approached not from a sense of static anatomy but from an appreciation of systematic and dynamic transformation and conservation of the totality. A whole is present if the elements of a structure are subordinated to the laws characterizing the system as such. Such laws cannot be reducible to cumulative associations but "confer on the whole as such over-all properties distinct from the properties of its elements".
In the next document we continue our investigation concerning the theory of organic lattices and seach for some preliminary validations of it among the facts and ideas as found in developmental biology (morphogenesis, especially embryology).
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-11.