

(Takes a little while loading the images)
e-mail :

Sequel-22 to the Summary and Evaluation (of the documents XVI -- XXVIII concerning the promorphology of complex-shaped two-dimensional crystals).
This document (Part XXIX Sequel-22) further elaborates on the analogy between crystals and organisms.
Sequel to the Preparations (X) to the Repertoire of the Crystal Analogy
Sequel (V) to Special Features of Crystals
Triangular snow crystals, summary and overview (II).
In this document we continue to list interesting and relevant snow crystals, i.e. relevant to the understanding of triangular snow crystals.
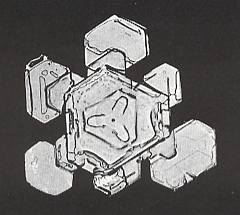


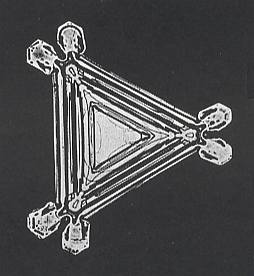
Figure above : Triangular snow crystal with outgrowths (the begining of arms or branches). The number of these outgrowths (six) indicates that the shape of the crystal, although nearly triangular, is that of an angle-ditrigon.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)
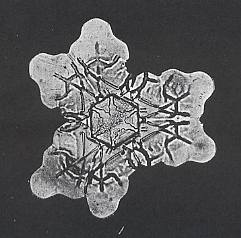




Figure above : A truly trigonal-hemihedric snow crystal, or a split-star?. If it is the latter, then it is holohedric. It then once was a capped column with branches at alternating positions (three at one end of the column, three alternate ones at its other end), as a result of competition for material (water molecules), that is to say, the developing star at one end of the (short) column competes during growth with the star at the other end of the column for material ( They compete, because these stars are situated so closely together), resulting in the development of only three (instead of six) arms in the first star, and only three (instead of six) arms in the second star that have alternate positions with respect to those of the first star. After that, the column, which is supposed to be just a slender axle, broke, resulting in the stars becoming separated. The intrinsic point symmetry of such a star is expected to be just holohedric, despite the fact that the morphological (or geometrical) symmetry is three-fold (as a result of the process described).
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)
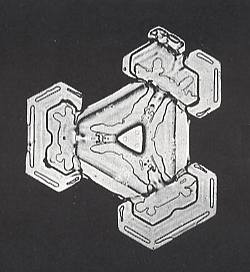
Figure above : Trigonal snow crystal that abruptly switches to holohedric symmetry, resulting in a shape according to the angle-ditrigon. Maybe it is more probable that the truly trigonal part of the crystal is only represented by the small equilateral triangle in its center, and that the peripheral structures are (two by two fused) outgrowths from an already holohedric crystal.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

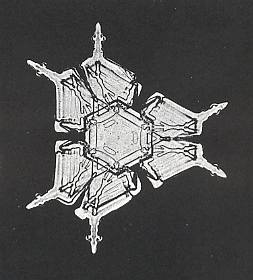
Figure above : Throughout trigonal snow crystal. In this crystal not only the notches are trigonally configured -- three broad ones, alternating with three narrow ones (which could just be the result of the distortion of the developing hexagonal plate), but also the substructures located at the level of these notches. The trigonal configuration of these substructures consists in the fact that each of the three narrow notches is flanked by a pair of these substructures, while the broad notches are not.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : Morphologically three-fold snow crystal. The configuration, as seen here, of three larger and three smaller arms could be the result of competition between the arms of one and the same star. If this is so, the crystal has crystallographically holohedric symmetry (i.e. with a six-fold rotation axis instead of a three-fold one). However, competition between the arms of one and the same star, leading to the dwarfing of a set of three (alternating) arms, seems unlikely, because we see so many star-shaped snow crystals with s i x fully and equally developed, broad arms (See next two Figures). So the nature of the three-foldness of this crystal is probably not only morphological but also crystallographic, meaning that the crystal is trigonal-hemihedric.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)

Figure above : A snow crystal with six equally developed broad arms. Most symmetrically developed snow crystals are like this.
(After LIBBRECHT, The Little Book of Snowflakes, 2004.

Figure above : Another example of a snow crystal with six equally developed broad arms, but here with a trigonal beginning.
(After LIBBRECHT, The Little Book of Snowflakes, 2004.

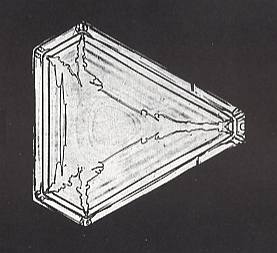
Figure above : Distorted triangular snow crystal, in fact a distorted angle-ditrigon. One radius of the trigonal stage initially failed to divide (leaving the crystal with only five faces), but later on finally did it, giving the crystal its sixth face. Compare with this Figure from the previous document .
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)





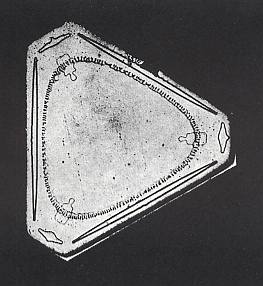









Figure above : A triangular crystal, but with the triangle already markedly truncated, in which the transition from trigonal-hemihedric to holohedric symmetry is clearly visible. Here we can see very well that the dividing lines between the faces (ending up at the corners separating actual faces) all diverge, indicating that all six faces will steadily increase when growth proceeds, meaning that no one of them will vanish, guaranteeing in this way the perpetuation of the angle-ditrigonal shape of the crystal. See next Figure, diagrammaticly explaining this.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)
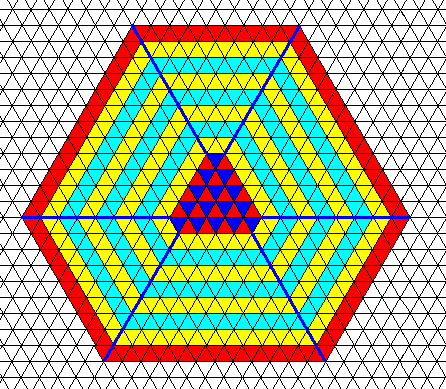
Figure above : An angle-ditrigonal crystal with a trigonal-hemihedric beginning (made evident by the differentiation between the two small triangles (red, dark blue) of a rhomb-shaped unit mesh of the hexagonal net). Beyond this trigonal-hemihedric beginning the crystal gives way to holohedric symmetry (expressed by the non-differentiation of those triangles (the color changes here only indicate growth layers, and, in addition, emphasize the last deposited layer). We see that the dividing lines separating the faces as they grow, are clearly divergent, meaning that all six faces will continue to extend, guaranteeing the perpetuation of the angle-ditrigonal shape of the crystal.

Figure above : Angle-ditrigonal snow crystal with extensive trigonal beginning, evident from substructures present in the crystal, which seem to be three by three different. The substructures' extensiveness or expansion (from the center towards the crystal boundary) apparently expressing the extension of the trigonal-hemihedric kernel (from center to boundary of crystal), could, however, be due just to the different sizes of the six faces (causing these substructures not to be (three by three) qualitatively different, but only (three by three) smaller (and thus qualitatively equal)), meaning that holohedric symmetry is already present in the distorted hexagon, implying that the transition to holohedric symmetry took place already much earlier in the crystal's individual history.
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)


Figure above : Snow crystal with extensive trigonal-hemihedric beginning (kernel), evident from the trigonal configuration of substructures. The alternate differences between these substructures are purely qualitative and not related to the relative magnitudes of crystal faces, meaning that indeed the trigonal-hemihedric kernel is large relative to the crystal's size.
Because the substructures (forming a trigonal pattern) are fairly complex, their almost exact 3-fold repetition is significant, and as such definitely points to true crystallographic trigonality. The small circular dots, visible on the crystal is rime (which is picked up by the crystal while falling through a cloud of supercooled water droplets).
(After BENTLEY & HUMPHREYS, 1931, Snow Crystals)




As is evident from all the above photographs (including those depicted in the previous document) trigonality, although representing a minority (because most symmetrically developed snow crystals are 6-fold), is nevertheless wide-spread, and thus does not represent just some (extrinsic) accidental events. And this means that trigonality, although not intrinsic to ice (1h) in general, is intrinsic for a great many snow crystals, and thus deserves extensive treatment and attention. The phenomenon teaches us a great deal about the crystallization process, a process evidently playing a major part in the crystal analogy to be expounded later on.
This concludes our discussion of special features in sterro-crystals.
e-mail :

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-23.