(Takes a little while loading the images)

e-mail : 

Back to Homepage

Introduction

Having established (previous two documents) the theory of organic lattices, based on the findings in snow crystals (still earlier documents) and on the need to account for the orderly spatial distribution of biological elements during organic morphogenesis, it is now time to systematically explore the existing analogies between crystals and organisms.
We can do so because we have uncovered the possible cause of these analogies, or at least one of the causes. This possible cause is the assumed organic lattice in organisms, which implies that we now can say that both organisms and crystals possess a lattice, accounting for their spatial structure. So these analogies could be (partially)  explained  by the presence of such a lattice, which in fact constitutes an  argument  in favor of the presence of such an organic lattice in organisms. But we must admit that an argument of that sort can never be a very convincing one, because all the analogies between crystals and organisms could well turn out to be merely trivial similarities, not in any way fundamental and significant :  There is, for example the growth analogy. Crystals do grow, as long as they find themselves in a suitable nutrient environment. There are even indications that the growth of crystals involves certain maxima. Also organisms do grow when situated in a suitable nutrient environment. In animals more or less definite maxima of attainable size are present, while many plants seem to be able to grow more or less indefinitely.
But growth, generally taken, is just an increase in size, which can happen everywhere, for example in mountain building as a result of an uplift of parts of the earth's crust, the increase in size of sand dunes when more and more sand grains accumulate by the action of the wind, and all other kinds of physical inflations. So the analogy could be trivial. Especially when extensive generalization is applied to certain concepts or types of processes, similarities appear even in unrelated phenomena.
However, we could retort that  genuine growth  is not just some increase in size and nothing more, but an orderly and repeatable increase in size of an intrinsic being,  and as such we see it only in crystals and organisms. It is true that organic growth is much more subtle than crystal growth, so it remains an analogy. But because of the regularity and repeatability, resulting in the  intrinsic nature of the  particular  way of growth of a given crystal or a given organism, the analogy is, in my opinion, not trivial.
The same applies to many other analogies between crystals and organisms.
So we'll take the crystal analogies seriously. And, as has been said, they are, at least partly, based on the supposed organic lattice in organisms. This organic lattice is meant to be a point lattice (quasi or true) where the points are provided with certain chemical units, motifs. And such  a  lattice + motifs,  i.e. a specified point lattice + fully specified motifs,  defines a crystal. The morphology (not only the symmetry) of the translation-free residue determines the promorph  or  stereometric basic form  of the crystal. And in the case of an  organic  crystal (resulting from an organic lattice) it is clear that its promorph determines the promorph of the  o r g a n i s m  possessing this organic crystal. As in any crystal, the number and configuration of its  antimers  can be expected (also) to be indicated by the configuration of outgrowths as they appear when the crystal grows fast, i.e. when the crystal is the result of non-equilibrium crystallization.
So while the  promorph of a true crystal  is based on its specified lattice + specified motifs (and from there (based) on the morphology of the translation-free residue), the  promorph of an organism  is an effect of the organism's underlying  o r g a n i c  lattice + motifs (both fully specified). However, the fact that organisms clearly do have a promorph cannot be used as a argument in favor of the presence of an organic lattice, because they can have a promorph without it, i.e. also structures that are in no way periodic do have a promorph.

To my knowledge, the most extensive exposition of the  crystal analogy  is offered in some of the works of  H. PRZIBRAM  (who influenced great embryologists like R. HARRISON), especially his  Die anorganischen Grenzbebiete der Biologie,  1926  (205 pages), where he explores a series of basic properties of organic and inorganic materials, comparing them, and using them for a theory of organic lattices.
Unfortunately this book is old (1926), and we can expect many details to be obsolete. Especially, in that time, little was known about the molecular basis of heredity. But it is the most recent book, extensively discussing this topic, I could lay my hands on. Therefore, in the present document, which is meant to be devoted to a presentation of a systematic crystal analogy, I will discuss this book's contents.
Apart from problems arising from its ancient date of appearance, the topic, discussed in this book, is a hard one already all by itself, because it requires acquaintance with many different disciplines, like physics (thermodynamics, hydrodynamics), chemistry (inorganic and organic), crystallography, mathematics, organic morphology, physiology, embryology, etc. Already for a long time, all these disciplines cannot be mastered at the same time by one and the same person. So the value of the content of such a book, like that of PRZIBRAM, as well as a modern commentary of it, is very limited indeed. Therefore my intention, when discussing the findings and ideas of this book, is not to give a body of technical and reliable knowledge, but to stimulate further reseach, or stimulate just a way of thinking about organisms and crystals. And this 'thinking about organisms' could consist of a further working-out of the theory of organic lattices, especially the version presented on this website, because this version does away with a number of problems inherent in PRZIBRAM's version. So it is the  frame-work  and the  approach  of the book (and my discussion of it), that is the most important aspect, not the many of its technical details (which should be re-checked).
While PRZIBRAM was thinking more or less in terms of real crystal lattices (of either solid crystals -- sterro-crystals, or liquid crystals -- rheo-crystals), our investigations, as were carried out in the previous documents, came to the conclusion that an  organic  lattice is conceptually and physically far more removed from a physical crystal lattice. For example it allows for its deformation while still remaining that same lattice, and can often act independently from the actions of other chemical units that are present within its interstitional space, both capabilities made possible by assumed compensating-reactions, unthinkable of in real crystals. Moreover, it is not the organism in the more strict sense that is crystalline (or quasi-crystalline) :  The organsmic organization of cells and tissues is something profoundly aperiodic. The supposed organic crystallinity is only a more or less hidden aspect of the organism, providing for some sort of spatial pre-design. The motifs at its lattice points could be centers from which emanate material or energetical gradients, instead of just being chemical units that only locally interact with each other resulting in their patterning. The organic lattice could even be no more than a convenient metaphor to  describe  organic structure, causing it to be analogous in a much stronger sense. Indeed, we know for sure that organisms are not crystals, also not non-equilibrium crystals. And the aspect of spatial organization and structure, for which to account we invoked organic lattices, is only one the many aspects of organic development. Another, and very important aspect, not accounted for by organic lattices, is the time aspect, i.e. the organization in time. We believe that much of this time aspect, consisting of the right time order of events in development, is taken care of by the organism's genome, its system of genes.
The fact that we devote so much attention to the  spatial  aspect of organisms and of their individual development is not that we consider it the most important feature, but because of the lack of attention it nowadays receives (apart from some ideas of positional information, material gradients, and the like). This lack of attention is probably due to the very promising  genetic  investigations (especially in molecular biology) which have already revealed so much for the understanding of life. But, as some authors have stressed, DNA cannot account for all features of life, and it can certainly not account for all spatial aspects in individual organisms.
As to the organic lattice, it is possible that more than one lattice, are involved, i.e. several more or less independent and partially overlapping lattices (as PRZIBRAM assumes) underlie the organism's spatial structure and spatial development.

So it is in the context of all the above that we must discuss PRZIBRAM's book on the crystal analogy.
PRZIBRAM, systematically considers certain phenomena, states, properties, processes, behavior and abilities that are being observed in organisms, and that seem to be peculiar to the latter. He then shows that these phenomena, states, etc. are also present in the inorganic world, albeit often in a more or less simplified version. In fact he demonstrates  analogies,  (and also smooth transitions), first of all between the organic and inorganic world, and sometimes, more specifically, between organisms and crystals. The motivation to do so is to demonstrate that the organic does not possess some fundamental 'extra' over and above the inorganic. In this way he argues against the vitalistic position, as for, instance held by his contemporary DRIESCH.  Along these lines he hopes then to become more specific by arguing that these analogies point to the existence of some periodic spatial point system (organic lattice) in organisms, and thus, because in crystals the presence of such a lattice is already definitely established, setting up a crystal analogy. In this way then one feature after another is discussed within this context.
First of all, under the heading of  "MORPHE",  he discusses morphological  (in the broad sense) phenomena (like  state of aggregation (solid, liquid, etc.),  state of dispersion (true solution, colloidal solution), basic form (promorph), growth, regeneration,  etc.), then, under the heading of  "PHYSIS",  he discusses  energetic statics,  energetic dynamics,  and  energetic kinetics.  Finally, under the heading of  "STEREOCHEMISTRY",  he discusses the features of, and directly connected with, the  microstructure  as we find it in crystals, and (as organic lattices) in organisms.
In commenting on all these features and phenomena, we must realize that PRZIBRAM'S book is from 1926, implying that some of his scientific background and, consequently, the corresponding conclusions drawn from it, could be more or less outdated. Moreover, some of the arguments, are more or less unclear, or are not so important anymore in the modern context.
Many of PRIZIBRAM's arguments involve areas of physics and chemistry that are not so familiar to me (making me heavily relying upon the writings of the several authors that are experts in these fields of enquiry).
For consulting the scientific backbround of PRZIBRAM (in order to understand and evaluate his arguments), I have, among other sources, made use of the  Handwörterbuch der Naturwissenschaften,  Ten Volumes (I--X), published in 1912--1915.  We will refer to it as HW-NAT (191x, Volume n, p.m).  Apart from giving us something of PRZIBRAM's scientific background, this extensive dictionary, compiled by many specialists of the time, contains -- if we limit ourselves to its general 'textbook' findings on classical physics and classical chemistry, and do not consider all too seriously certain molecular or atomic hyphotheses and other aspects liable to being superseded by new insights -- much information that is still valuable today, certainly when it is used for more general qualitative and philosophically oriented discussions, as they are taking place on this website.
For commenting PRZIBRAM's theory, it was also necessary to consult books of a more recent origin, that consider some of the mentioned phenomena. Among these books are :  Introductory Chemistry,  by R. OUELLETTE, 1970,  (referred to as OUELLETTE, 1970) and  Disigning the Molecular World, Chemistry at the Frontier,  by Ph. BALL, 1994,  (referred to as BALL, 1994).
In commenting on the expositions of PRZIBRAM (in his mentiond book -- 1926 -- on the crystal analogy, 205 pages) we will then proceed as follows :
Where necessary, we will begin with a general exposition of the feature or phenomenon that PRZIBRAM is about to discuss in the relevant section of his book. After that we will discuss and evaluate PRIZIBRAM's argument with respect to that particular feature. Then we take the next feature, discussed by PRZIBRAM, and again, when necessary, we start with a general exposition about that feature, followed by a discusssion and evaluation of PRZIBRAM'a argument in with this feature plays a role. etc.
However, in order not to interrupt the arguments too long and too often, we shall first give a general exposition of some important topics, such as the thermodynamics with respect to crystallization and the theory of liquid crystals.

The ensuing exposition is about the conditions that must be satisfied for a chemical or physical transformation to be possible at all. We will focus as much as we can on the crystallization process, and especially that process in which only one chemical compound is involved (for example the formation of snow crystals from water vapor). Such a system is a so-called one-component system. Let us start with the theory of phases, that is to say the theory that considers the possible existence of a given phase and the coexistence of several different phases (like, for instance ice-water-steam).
We will derive the  phase rule  which, by means of an equation, relates, in a given system, the number of phases (P), the number of independent components (C) (as types, not as particles) and the number of degrees of freedom (F). This  phase rule  reads :

In order to derive this rule, we must first clarify some conceps (In what follows, viz., concepts and derivation, is taken from HW-NAT (1912, Volume VII, pp.678).

Phases, in the sense of the theory of phases, are  spatial  states, and thus states of aggregation. So there are solid, liquid and gaseous phases (Colloids also represent a certain state of aggregation. But for colloids  surface tension  is highly important to their resulting form. And because in the ensuing derivation of the phase rule surface tension is neglected, the phase rule, at least in its ordinary form, does not apply to colloids).
In a heterogeneous system many solid phases can be present, but maximally only two liquid phases, and only one gaseous phase. A characteristic feature of a phase is its homogeneity. In contrast to a chemical compound, a phase, in its molecular dimensions, does not need to be an intrinsic unity, or body. Consequently a mixture of gases, a solution or a mixed crystal, represents one single phase.

Independent components (or, simply, 'components') of a system are those components that cannot be produced by the mixing of other components of the system. The selection of these independent components must comply with two conditions :  (1) Every possible change in the composition of phases of the given system must be expressible by the change in quantity of these independent components.  (2) The latter changes must be independent of each other.
So one must select the smallest possible number of independent components.
For systems which interest us most, viz., the crystallization of a single compound from its solution, from its melt or from its vapor, the number of independent components (C) is 1.

The  degree of freedom  (F) is the difference between the number of variables of a given system and the number of equations that determine these variables.
For example if have one variable and one equation determining it, then this variable is totally determined, i.e. it is fixed, and consequently is has no degree of freedom, or could we say, the number of degrees of freedom is zero. Such a variable could be  x,  and the equation could be  2x + 5 = 0,  implying that  x  is fixed to be equal to minus two and a half (-5/2).
If, on the other hand, we have two variables,  x  and  y,  and only one equation, say,  2x + y = 5,  then when  x  is determined then also is  y .  When, however,  x  gets a new value, different from the first one, then the value of  y  will be different too. The number of degrees of freedom is now 1, because only either  x  can be varied (and then fixing all the corresponding values for  y),  or  y  can be varied (and then fixing all the corresponding values of  x).

Most fundamental are the First and Second Laws of Thermodynamics.
The botom line of these laws is that they reject the possibility of a  perpetuum mobile .  (i.e. a machine that keeps on running without the need for further and continued (re)fuelling). The possibility one kind of perpetuum mobile is denied by the First Law, while a second kind is denied by the Second Law.

The  First Law  can be stated mathematically as follows :

Where  dQ  is the amount of heat supply,
dE  is the increase of interior energy of the system,
dV  is the increase of volume, and
p  is the pressure.

The  Second Law  can be stated mathematically as follows :

Where  " / "  means 'divided by',
dS  is the increase of entropy,
T  is the absolute temperature, and
DELTA  is a positive quantity (in the limiting case :  zero).
Entropy (S) is a measure of disorder of the given system.

The  Second Law  can verbally be stated as follow :
All realizable transformations are accompanied by an increase in the total amount of  entropy  in the Universe (Strictly speaking, it says that the entropy cannot decrease. There is a class of transformations -- those that can be reversed exactly -- for which the entropy content of the Universe can remain unchanged). (See BALL, 1994, p.57).
The above given mathematical expression of the Second Law can verbally be read as follows :  Even when the supplied heat  dQ  is zero, i.e. even when the interior energy (E) and the volume (V) of the system remain what they were, (making  dQ / T  equal to zero), the change in entropy is still positive or zero, i.e. it does not decrease :  dS (E and V constant) = DELTA.  So in a closed system the entropy (S) remains either the same or increases,  dS = 0  or  dS > 0.
The  " divided by T "  in the mathematical expression of the Second Law, can, I think, loosely be interpreted as preventing  dS  (change of entropy)  to rise indefinitely.

About the Second Law  BALL, 1994, p.57, writes the following :

These days, entropy is a term not uncommon in everyday parlance, but it has acquired a certain air of mystery. There is, however, nothing very mysterious about it at all. It can be regarded as a measure of disorder -- a pile of bricks, for instance, has more entropy than a house. Similarly, a liquid has a greater entropy than a crystal, since  [ in ]  the former the molecules tumble about in disarray while in the latter they are stacked in an oderly, regular pattern  [Nevertheless a crystal can spontaneously emerge from a melt or solution, because the entropy ends up in the crystal's environment, and it is the total entropy count that matters ] .  The Second Law is therefore saying that the Universe is bound to become ever more disorderly. This too can appear to be a very recondite and mysterious statement, but in fact it is saying nothing more than that things tend to happen in the most probable way :  there is simply a greater probability that things will become disordered than the reverse. The Second Law is therefore actually a statistical law, which does not prohibit absolutely the possibility of a change that induces a decrease in entropy, but says only that such a change is overwhelmingly unlikely when we are considering huge numbers of molecules  [ because they admit of many many different configurations, and most of them are disordered ].

Willard Gibbs (a nineteenth century scientist) expressed the directionality criterion in terms of a quantity called the Gibbs free energy, which quantifies the net effect of the various contributions on the total change in entropy during the transformation. These contributions are :

• Entropy change of the materials taking part, or being the result, of the transformation.
• Amount of heat taken in or given out.
• Work done on the surroundings.

But even when a given transformation happens to be geared towards a boost for the total entropy of the Universe, which is to say, going to effect a large decrease in Gibbs free energy, it often doesn't get started. Indeed, the Gibbs free energy criterion, i.e. the thermodynamics, only decides whether a particular transformation is physically feasable at all. What hinders the transformation from actually proceeding is the kinetics of that transformation.
Indeed, the initial step of a transformation is generally an  uphill  process :  energy must be supplied to get things going. That is, that although a transformation can itself be a downhill process (which means that it does not need to be sustained by energy supply from without), it can involve an energy barrier, that must be taken, before the transformation will proceed and will be self-supporting. This is the case when we ignite paper in order to burn it. And the same is the case in supercooled liquids. These are liquids that ought to be in the solid state, but still are not. But one or another disturbance (which we can interpret as an energy nudge) sets solidification in motion, the liquid freezes. While the difference in Gibbs free energy involved in a transformation, determines the position of the equilibrium of the transformation, the kinetic hindrance controls its speed. But apart from this initial barrier -- which makes  a system to be in an unstable state  possible (especially relevant when this barrier is very small) -- the Gibbs free energy (and also the thermodynamic potential, which we assume to be equivalent) must decrease.  BALL, 1994, p.58, remarks that strictly speaking, this latter is true only when the temperature and pressure of the system are held constant. Under different conditions, other kinds of free energy must be considered instead of that defined by Gibbs. But if everything has free play, then in phase transitions (which are our main concern here), like the formation of snow crystals or the melting of a metal, pressure and temperature indeed remain constant.

Because of the difficulty to understand all the factors involved in chemical and physical transformations, including phase transitions, we will cite yet another author, who gives a qualitative account of the thermodynamic feasability and determination of the direction of transformations, using the concepts of  ENTHALPY,  ENTROPY  and  FREE ENERGY (the latter I assume to be the Gibbs free energy mentioned earlier). The quote is from R. OUELLETTE, Introductory Chemistry, 1970, p.211--212 [comments between square brackets] :

The equilibrium state for both physical and chemical systems can be treated quantitatively by means of thermodynamics. While the concepts and implications of thermodynamics will not be covered rigorously in this text, there are certain basic features that can be qualitatively described  [...] .
There are many physical and chemical processes that occur naturally. The flow of water downhill and the expansion of a gas to fill a container are two examples of spontaneous physical processes. The reaction of hydrogen and oxygen to yield water and the burning of wood are examples of chemical processes. Analysis of all naturally occurring processes reveals that two fundamental features control them. Most  [ and thus not all ]  systems tend to produce a state of lower energy  [ not to be confused with the Gibbs free energy, i.e. this energy is not yet the Gibbs free energy ]  and as a consequence release the net energy difference between the initial state and the final state. The reverse process is less common and can occur only if the second controlling feature, entropy change, is favorable  [ and that means that the total entropy increases ] .  The flow of water downhill and liberation of heat in the formation of water from hydrogen and oxygen occur because a state of lower energy is achieved. In such cases the energy difference between initial and final states is called the change in  enthalpy,  delta H.  By convention the liberation of energy is given a negative sign. For example, the reaction

CO₂ + H₂ ==> CO + H₂O

liberates 9830 cal for each mole of CO₂ that reacts. The enthalpy change, delta H = - 9830 cal/mole, reflects the fact that the products CO and H₂O are more stable than CO₂ and H₂ by 9830 cal/mole.
The second controlling feature of all processes is the tendency of a system to achieve the most random or disordered arrangement possible  [ because such arrangements are the vast majority of all logically possible arrangements, and are therefore, as a class, more probable ] .  This feature is important  [ i.e. dominant ]  in the expansion of a gas or the vaporization of a liquid  [...].  The degree of randomness or disorder is called the  entropy  of a system. By definition the entropy change (delta S) is positive for increasing disorder. The entropy change counterbalances unfavorable enthalpy changes in some systems. If the increase in the degree of disorder is great, an endothermic process can occur  [ an endothermic process is a process that must be supplied by energy from without if it is to be maintained ].
The temperature is a significant factor in determining the relative importance of enthalpy and entropy contributions to a system that can undergo change. At absolute zero all substances are ordered and entropy differences between two or more substances are zero. Therefore, only their relative energies determine their relative stabilities. With an increase in temperature a variety of molecular motions become[s] possible, and the tendency toward disorder changes from substance to substance. The differences in entropy can play a variable role as a function of temperature. At extremely high temperatures the entropy differences between various substances may play a dominant role in the course of a reaction.
The relationship between enthalpy changes and entropy changes is given by the following expression, in which  delta G  symbolizes the change in  [ Gibbs ]  free energy  of a system at constant pressure :

delta H - T.delta S = delta G

[ which, verbally reads :  The change in enthalpy minus the product of the absolute temperature and the change of entropy is equal to the change of Gibbs free energy.]

The free energy change is a measure of the driving force of a reaction or the tendency of it to proceed spontaneously. When  delta G  is negative a chemical or physical process occurs. The negative enthalpy change previously described as being important in determining the course of a reaction can be seen to contribute toward making  delta G  more negative. Similarly, a positive entropy change contributes toward making  delta G  negative. From the expression it can be seen that  delta H  is more important at low temperatures and  delta S  becomes more important at high temperatures.
The power of thermodynamics stems from the potential to be able to calculate whether or not a hypothetical reaction will proceed in a desired manner. Tables of enthalpies and entropies of substances are available, and by arithmetical addition and subtraction the free energy difference between two possible sets of substances  [  i.e. a set before, and a set resulting from, the reaction ]  can be calculated. If  delta G  is negative the reaction can proceed spontaneously in the direction desired. However, the difference in free energy does not indicate the velocity of the reaction since the rate is dependent on the activation energy  [ i.e. the energy needed to overcome the energy barrier mentioned above ]  and not the difference in energy between reactants and products. Therefore, the spontaneous or naturally occurring processes may proceed at very slow rates  [ (catalysts can lower the energy barrier, and so speed up the reaction) ] .
The size of the free energy change between reactants and products determines the position of equilibrium.

We will now proceed with the derivation of the phase rule, basing ourselves on the expositions in HW-NAT, volume VII, pp.679.

As already stated above, the  First Law  of thermodynamics can be stated mathematically as follows :

Where  dQ  is the amount of heat supply,
dE  is the increase of interior energy of the system,
dV  is the increase of volume, and
p  is the pressure.

While the  Second Law  of thermodynamics can be stated mathematically as :

Where  " / "  means 'divided by',
dS  is the increase of entropy,
T  is the absolute temperature, and
DELTA  is a positive quantity (in the limiting case :  zero).
Entropy (S) is a measure of disorder of the given system.

Where  "T. DELTA"  means :  absolute temperature times DELTA.

When E and V are constant (thus dE = 0 and dV = 0) we then get :

The entropy change of a system having a constant volume and constant interior energy is accordingly always positive (or zero). So if we have a number of particles inside a closed volume, such that neither from the latter to the exterior, nor from the exterior into the interior, energy changes are taking place, then in chemical or physical changes (transformations) of the system, then the total inner entropy always increases (or, in a limiting case, stays the same, namely in the case of completely reversible processes, if such exist). When that entropy has reached its highest possible value, then, say, in virtue of some virtual change taking place, no increase in entropy can be the result anymore :  equilibrium is attained.
For the derivation if the phase rule the entropy is less suitable. For this purpose it is better to begin with the  thermodynamic potential,  introduced by GIBBS :

As has been said, we assume this potential to be equivalent to the Gibbs free energy.
When we differentiate this equation, i.e. if we want to determine the rate of change of this thermodynamic potential during a transformation, we get :

or, when using equation (3)  :

So when the temperature is constant and the pressure is constant (dT = 0 and dp = 0), we have :

where  "- T. DELTA"  (i.e. minus T. DELTA) is -- because T is always positive (in the case of it being zero, there can be no transformations taking place at all) -- always negative, because, except in the limiting case,  T. DELTA  is always positive. So if the temperature and pressure are given, then a complex of particles can undergo only such changes that cause the thermodynamic potential to decrease.

(but recall that  delta  (as used here) refers to a difference, while  d  refers to a differential), that was discussed in the mentioned quote from OUELLETTE.  And this indicates the close relationship between the  thermodynamic potential  (Z) and the  Gibbs free energy (G).
If we, instead of using equation (4a), we use equation (5) -- which was derived from equation (4a) by using equation (3) --, then we get, when T and p (temperature and pressure) are held constant,  dZ_{(T, p)} = - T. DELTA,  which we got earlier.  And in this way we do not have to assume a constant volume, and, moreover, directly obtain an expression which shows that a transformation will only take place when the thermodynamical potential decreases. The same holds, as we already know, for the Gibbs free energy.
(End of note)

The classification of the different systems is most convenient when based on the number of independent components. One distinguishes one-, two-, three- and multi-component systems, as C = 1, 2, 3, etc.  Further one indicates, on the basis of  F = 0, 1, 2, etc., the systems as invariant, monovariant, bivariant, etc.
If  F = 0,  the number of degrees of freedom is zero, and the corresponding equilibrium is invariant. Its graphical expression is a point.
If  F = 1,  the number of degrees of freedom is one, and the corresponding equilibrium is monovariant. Its graphical expression is a line.
If  F = 2,  the number of degrees of freedom is two, and the corresponding equilibrium is bivariant. Its graphical expression is a plane.
etc. (See below)
Of the magnitudes, which, apart from concentration, are important in a system, viz., interior energy, entropy, thermodynamic potential, volume, temperature and pressure, only the latter three can be indicated by their absolute values, while of the remaining magnitudes only their changes can be measured, not their absolute values. Therefore, for most cases one only considers the relations between volume, temperature and pressure alongside (in the case of two- and multi-component systems) the concentrations. And often also volume is, in virtue of its lesser importance, not expressed.

In a one-component system, i.e. a system consisting of only one independent component (C = 1), the phase rule is  P + F = 3  (P + F = 1 + 2).
If the equilibrium is invariant, i.e. if F = 0, then P = 3, i.e. the number of phases is three.
Every invariant equilibrium, i.e. an equilibrium having no freedom anymore, is characterized by a set of constant values (for temperature, pressure and volume). The point, expressing an invariant equilibrium in a one-component system, contains three phases, and is called the  triple point.  At the values of temperature, pressure, etc. determining this triple point, three phases can coexist together (in the case of H₂O, for example, the vapor phase (steam), the liquid phase (water) and the solid phase (ice).
In a diagram, expressing the relationship between temperature and pressure, three curves indicate the stability areas of the different phases, and these three curves meet in a point, the triple point, representing the invariant equilibrium of these three phases. See next Figure.

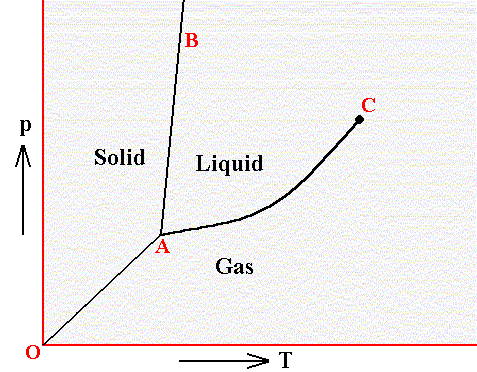
Figure above :  Phase diagram of a one-component system (C = 1). It shows the pressure-temperature  ( p-T )  borders between the three states (phases) of solid, liquid and gas of a substance. Borders define the conditions of pressure and temperature at which phase transitions such as melting and freezing occur. Point A is the  triple point  at which all three phases are in equilibrium. At point O the pressure and the absolute temperature are zero.
The border between the liquid area and the gas area stops abruptly at the critical point C, which is unstable. To the right of this point there is no border, which means that in that area there is no distinction between liquid and gas.
The directions of the borders and the extent of the areas depend on the substance involved in the diagram. The solid-liquid boundary (AB) is for most substances steep, and heading NNE, as in the present diagram. Water, on the other hand, is more or less abnormal. For it the solid-liquid boundary runs NNW, as a consequence of the fact that the density of ice is less than that of (liquid) water.

Every uniform substance that melts without being broken down, be it a chemical element or compound, possesses a triple point. The position of that point in a pT diagram (i.e. a diagram indicating the relation between pressure (p) and temperature (T), as in the above Figure), says something about the behavior of the substance (or material body) with respect to pressure and temperature.
If the pressure in the triple point of a given substance is higher than the atmospheric pressure (1 Atm), then one can melt this substance only 'under pressure' (which here means a pressure higher than 1 Atm), because only at the triple point pressure the system solid-liquid-gas becomes possible. Examples are arsenic, carbon dioxide and carbon. As a result of heat supply such substances change, at atmospheric pressure, from solid to gas (sublimation), at a specific temperature. This sublimation temperature is lower than that of the triple point and very dependent on pressure. When pressure is increased it eventually goes over into the temperature of the triple point. See next Figure.

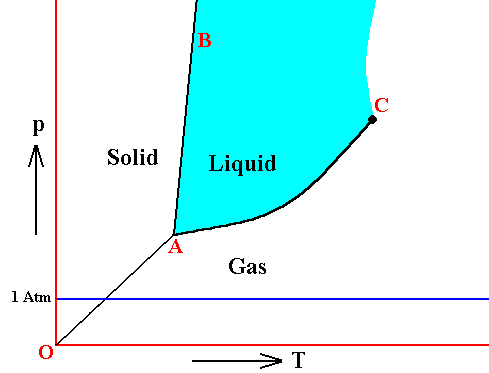
Figure above :  Same as previous Figure. Phase diagram of a one-component system (C = 1). Liquid stability area indicated by blue coloring. The substance involved is, in the present Figure, supposed to have its triple point pressure higher than 1 Atm. If the pressure of the system is increased, the sublimation temperature increases, till it is equal to the pressure at the triple point, where the liquid phase becomes possible. When the pressure has increased (not too far) beyond the triple point pressure, then the corresponding substance will pass from the solid state into the liquid state (i.e. it melts), when the temperature reaches a certain value (which is the melting point at that particular pressure).

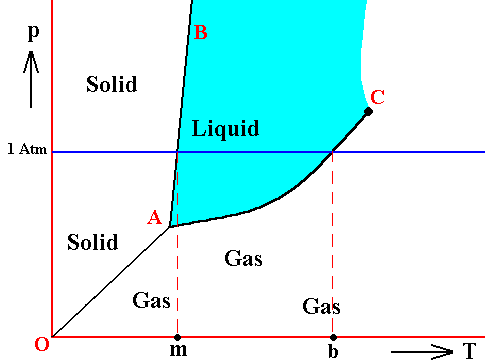
Figure above :  Same as previous Figures. Phase diagram of a one-component system (C = 1). Liquid stability area indicated by blue coloring. The substance involved is, in the present Figure, supposed to have its triple point pressure lower than 1 Atm.
m  is the melting point of the substance at atmospheric pressure, and  b  is its boiling point at atmospheric pressure.

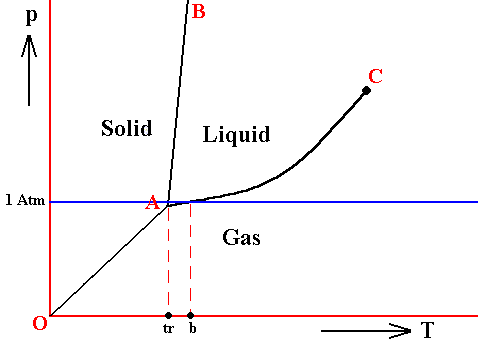
Figure above :  Same as previous Figures. Phase diagram of a one-component system (C = 1). The substance involved is, in the present Figure, supposed to have its triple-point pressure close to 1 Atm.   A = triple point.
tr  is the triple-point temperature, and  b  is the boiling point of the substance at atmospheric pressure. The lie close to each other.

If, in metals, or other materials, with high melting points the triple-point pressure is very low (which implies that there is a large difference between melting point and boiling point), then the temperature at which such substances boil at atmospheric pressure is very high indeed, and can hardly, if at all, be realized with mundane equipment. However, in strongly evacuated containers, where now the pressure is close to the triple-point pressure of these materials, the boiling point has come closer to the melting point (which itself generally varies little with pressure), and indeed in this way one was able to boil these substances.

When a liquid evaporates below its boiling point it will cool. The next consideration explains this by describing the evaporation in kinetic terms. For this we will quote OUELLETTE, 1970, Introductory chemistry, from page p.64, 65, 67 and 68.

In the liquid phase, as in the gaseous phase, there is a distribution of particles of different kinetic energies [ i.e. energy of motion ] .  The most energetic particles leave the liquid phase most readily, causing a decrease in the average kinetic energy of the remaining particles. This is felt as a lowering in the temperature of the liquid. The evaporation process continues at the same rate if a heat source is available to maintain the temperature of the liquid. A glass of water in a closed room  [ i.e. in a large but not infinite environment ]  without air currents will evaporate without any noticeable cooling. As the most energetic particles leave the liquid phase, heat is transferred from the surroundings to the liquid, maintaining the temperature. A redistribution of particles with various kinetic energies yields the same Maxwell-Boltzmann distribution as existed before the most energetic particles left.
Evaporation of matter from the liquid phase is less likely as the temperature decreases, since the average kinetic energy of the particles and hence their ability to escape into the gaseous phase decreases  [...].
Even at the same temperature, different liquids evaporate at different rates  [...].  The ease of evaporation in the liquid phase is a function of the liquid. Since the average kinetic energies of particles in two different liquids at the same temperature are identical, the escaping tendency must be controlled by the attractive forces between neighbors. If attractive forces between neighboring particles are large, the escaping ability of a given particle is retarded by its neighbors  [...].
Evaporation from an open vessel indicates that the liquid particles have an escaping tendency. This tendency also should be manifested in a closed vessel. However, when a liquid is placed in a closed vessel there is only a small decrease in the volume of the liquid with time. This should not be too unexpected because the densities of matter in the liquid and gaseous phases are drastically different. Evaporation of a small quantity of liquid results in a large volume of gas. Whenever a liquid is placed in a closed vessel, particles leave the liquid phase and enter the gaseous phase. As the number of particles in the gaseous phase increases, it becomes more likely that they will collide with the liquid surface and return to it. Eventually a balance is achieved :  The rates at which the particles leave and return to the liquid phase become equal  [...].  When such a balance occurs, the system is in equilibrium.  In a system at equilibrium no net macroscopic change occurs. Various submicroscopic processes, such as evaporation and condensation, occur continuously, but in such a manner that they balance each other.
The particles in the gas phase exert a pressure like those of any gas. This pressure of a gas in equilibrium with its liquid phase is called the  vapor pressure  of the liquid  [...].  It indicates the escaping tendency of the liquid, which in turn is characteristic of the individual liquid and its temperature  [...].
Evaporation as a physical process is rather unspectacular, but upon heating to a specific temperature any liquid eventually will undergo a very pronounced transformation. Bubbles are formed throughout the liquid, and they rise rapidly to the surface, bursting and releasing vapor in large quantities. This process is called boiling, and the temperature at which it occurs is called the boiling point of the liquid. At the boiling point it can be shown experimentally that the vapor pressure of the liquid is equal to that of atmospheric pressure  [ generally, equal to the prevailing pressure of the system ] .  Owing to the large escaping tendency of the liquid at its boiling point, bubbles of vapor may be formed within the volume of the liquid. This is in contrast to the process of evaporation that is largely a surface phenonenon.

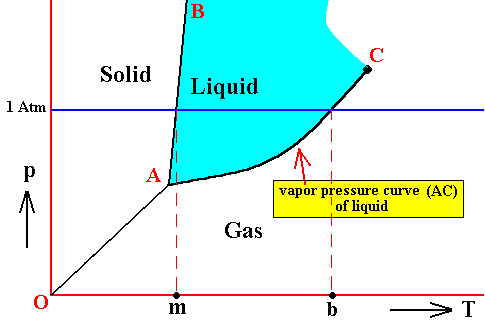
Figure above :  Phase diagram of a one-component system (C = 1). The substance involved is, in the present Figure, supposed to have its triple-point pressure lower than 1 Atm.
m  is the melting point of the substance at atmospheric pressure, and  b  is its boiling point at atmospheric pressure.
The curve AC expresses the increase of the vapor pressure of the liquid with increasing temperature. When this vapor pressure reaches the prevailing pressure of the system, the liquid will boil. That the curve AC must be the vapor-pressure curve (for the liquid) follows from the fact that the vapor pressure of a liquid is only defined under equilibrium conditions, i.e. when the liquid is in equilibrium with its gas phase.
So if the prevailing pressure happens to be 1 Atm, then the liquid will boil when its vapor pressure has (because of increasing temperature) become equal to 1 Atm. The corresponding temperature where this happens is the boiling temperature of the substance at 1 Atm.

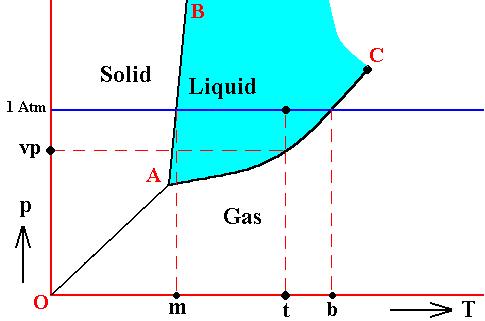
Figure above :  Phase diagram of a one-component system (C = 1). The substance involved is, in the present Figure, supposed to have its triple-point pressure lower than 1 Atm.
m  is the melting point of the substance at atmospheric pressure, and  b  is its boiling point at atmospheric pressure.
The curve AC expresses the increase of the vapor pressure of the liquid with increasing temperature. If this substance finds itself under the condition of temperature  t  and a pressure of 1 Atm, then its vapor pressure is  vp.

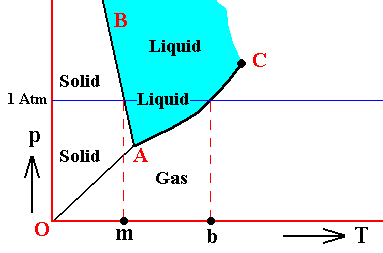
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point,  AB = melting curve,  AC = vapor-pressure curve of liquid water,  OA = vapor pressure curve of solid water (ice),  C = critical point,  m = melting point (273⁰K = 0⁰C) at 1 Atm,  b = boiling point (373⁰K = 100⁰C) at 1 Atm.
The phase diagram of water is subtly different from that of most substances. The solid-liquid boundary slopes NNW, not NNE. This is a direct consequence of the fact that water has the unusual property of getting less dense when it freezes. The triple-point pressure of H₂O is 4.6 mm mercury, and its triple-point temperature is 0.007⁰C (See also BALL, Ph.,  H₂O,  a Biography of Water, 1999, 2000, p.150).

Solids, like liquids, have a vapor pressure. However, the idea that a solid can evaporate is not as common among the nonscientific community as the concept of evaporation of liquids. The evaporation of ice is the reason that even frozen clothes will dry outdours in subzero weather. The vaporization of solid carbon dioxide (Dry Ice) and mothballs are other common examples.
The kinetic theory applies to solids in much the same way as to liquids. Particles in the solid state  [ i.e. in the context of a (macroscopic) solid ]  have a range of energies and are distributed among the energies according to the Boltzmann curve. Those of the more energetic particles that lie at the surface of the solid can escape into the gas phase. This is in contrast to the liquid state, in which the mobility of the particles may result in the transfer of a particle from deep within the liquid to the surface where it may escape.
The vapor pressure of a solid can be measured by the same apparatus  [ as in the case ]  [...] of the vapor pressure of a liquid [...].  As is the case with liquids, the vapor pressure is a measure of an equilibrium process. If a solid such as ice is placed in a closed container, the most energetic surface particles escape. However, eventually the gaseous particles return to the solid. The pressure of the vapor gradually increases to a maximum value. Then, the rate of escape is equal to the rate of return to the solid.
The larger the attractive forces between molecules or atoms, the smaller will be the vapor pressure of the solid. With increasing temperature the vapor pressure of the solid increases, because the average kinetic energy of the particles increases. However, the vapor pressure of most solids rarely gets very large since the solid usually melts at high temperatures. For most solids the tendency to enter the liquid phase is larger than that for entering the gaseous phase. Dry Ice, solid carbon dioxide, is an exception in that upon heating it is converted directly to the gaseous state. The liquid state  [ of carbon dioxide ]  is not observed at atmospheric pressure. Direct vaporization of a solid without melting is called sublimation.

Le Châtelier in 1884 proposed a principle that predicts the behavior of an equilibrium when it is subjected to an external force :  If an external force is applied to a system at equilibrium, the system will readjust to reduce the stress imposed upon it if possible. This principle, which is intuitively reasonable, explains the effect of pressure on the boiling point of a liquid and the melting point of a solid. In the first case, evaporation of a liquid always involves a tremendous increase in volume. Application of pressure will cause the equilibrium system of a liquid and its vapor at its normal boiling point to shift toward the liquid state, because the resultant decrease in volume tends to diminish the pressure on the equilibrium system. Therefore, in order to boil a liquid at high pressures, higher temperatures are necessary. In the case of the melting point of a solid, most substances decrease in volume in going from the liquid to the solid state, and application of pressure will cause an equilibrium system of liquid and solid to shift toward the solid state. This shift decreases the volume of the system and counteracts the applied pressure. Therefore, in order to melt most solids under pressure, higher temperatures are necessary. That only small increases in melting points are usually observed is a reflection of the small change in volume between solids and liquids. The abnormal behavior of water is the result of the increase in volume of this compound in going from water to ice. Thus, an increase in pressure shifts ice-water systems toward water.

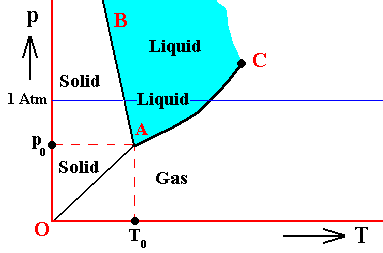
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point.
If the condition (state) of the H₂O system is  T₀p₀ ,  i.e. if the temperature of this system is  T₀  and the pressure  p₀ ,  then the vapor pressure of the solid is equal to that of the liquid. So the solid is not forced to either increase or decrease the vapor pressure in order to achieve a balance with the liquid. And so for the liquid. But because there now is no net inflow or outflow of vapor into and from solid or liquid, the vapor phase is static too. So all three phases are in equilibrium  (i.e. they can all coexist at the same time) when the state of the system is  T₀p₀ .  Therefore, the point (T₀, p₀) is called the triple point of the system. The triple-point pressure of water (p₀) is 4.6 mm mercury, and its triple-point temperature (T₀) is 0.007⁰C  ( = 273⁰K ).

If --- things are taken here from HW-NAT (Handwörterbuch der Naturwissenschaften, 1912--1915), VII, p.680 --- there are monovariant equilibria in one-component systems, i.e. when F = 1,  then P = 2 (i.e. the number of phases is two). In the presence of two phases we still have one freedom, i.e. within the range in which equilibrium between the relevant two phases is possible at all, one can, among the determining factors (for instance pressure, temperature, volume, etc.), still choose a value of one of them as one pleases, and not until then all magnitudes relating to the equilibrium are fixed. One such monovariant equilibrium is the curve that leads from zero pressure and zero temperature (the point O in our phase diagrams) to the triple point (A). It is the sublimation curve, OA, on which lie all the points (temperature-pressure coordinates) in which the solid state (phase) is in equilibrium with the gaseous state (phase). It is at the same time the vapor-pressure curve of the solid.
A second monovariant equilibrium exists between solid and liquid. This melting curve runs from the triple point generally steeply upwards (AB in our phase diagrams), resulting in only a small deviation of the melting point at the triple point (for example ice, 0.007⁰C) from that at atmospheric pressure (0⁰C). The deviation, positive or negative, depends on the volume taken up by the given substance in its solid or liquid state. If the volume of the solid state is larger than that of the liquid state (as, for instance in the ice-water system), then the melting temperature decreases with increasing pressure (as is evident from Lechâtelier's princple mentioned above). In many other substances, on the other hand, the melting temperature increases with pressure :  in the solid state the volume is smaller than in the liquid state, which means that at solidification the solid parts sink to the bottom of the melt (while in water this is the other way around, so that ice-bergs float on the water). At each point of this curve the solid phase is in equilibrium with the liquid phase.
Finally, the third monovariant equilibrium -- liquid-gas -- in one-component systems, is the boiling curve or vapor-pressure curve of the liquid, running from the triple point in about a NE direction in the phase diagram (AC). It ends in the critical point C.  At each point on this curve the liquid phase is in equilibrium with the gaseous phase.

Bivariant or divariant equilibria (F = 2) in a one-component system, exist, according to the phase rule (P + F = C + 2), at the presence of only one phase (P = 1). As a result of this dual variability, the phases viz., solid, liquid, gaseous (and supercritical), are, in the phase diagram, depicted as plane areas, bounded by the curves representing the monovariant equilibria.

The concept of a bivariant equilibrium is a strange one at first sight. An equilibrium implies two entities that balance each other. But in a bivariant equilibrium of a one-component system only one phase can be present. So this phase must be in equilibrium with itself. This is, without qualification, possible for a gas, for example water vapor under a pressure of 1 Atm and having a temperature of 120⁰C (or any other temperature moderately above water's normal boiling point). But solids and liquids always give off vapor and thus, when there is equilibrium, it is always equilibrium with their corresponding gas phase :  The rate of particles leaving the solid or the liquid is equal to the rate of particles returning to them, and thus two phases are involved in the equilibrium. So when, if ever, will we see an equilibrium that involves only one phase? Well, according to me, we must think of the  interior  of a given solid or of a given liquid, when such a solid or liquid finds itself in pressure-temperature (P/T) conditions corresponding to the 'solid' or 'liquid' area of the triple-point diagram. So if we have a mass of solid, or a mass of liquid under the mentioned P/T conditions, then any volume within its interior (i.e. any volume that does not include any interface -- or 'interphase') is in equilibrium with itself.
For a solid to be in equilibrium with itself, this is directly clear, because its constituents do not wander around. So for any volume totally within its interface boundaries, the rate of incoming particles is equal to the rate of outcoming particles, namely zero.
For a liquid to be in equilibrium with itself, we can say that the traffic into and the traffic out of such an interior volume balance each other.
And indeed the same can be said of any interior volume of a given gas. When the gas is in equilibrium with itself, there is a balance between the traffics into and out of such an interior volume representing the gas.

If given substances are held in pressure-temperature conditions which do not correspond to their aggregation condition (solid, liquid, gas), for example liquid water held below 0⁰C (at atmospheric pressure) -- a phenomenon called undercooling -- then they find themselves in an unstable condition and the stable equilibrium is often quickly restored when seeded or shaken. The next Figures illustrate this. In doing so, they consider one-component thermodynamic systems in general, using the  ice-water-steam system  as an example. So in this context the latter system must be seen as it is in itself, and not as contained within an overall matrix as is the case in our atmosphere (which situation will be discussed further below).  If, in relevant examples, we nevertheless suppose the system to be mixed up with air (not necessarily resulting in a total pressure of 1 Atm, as it does in the atmosphere), we will say so.

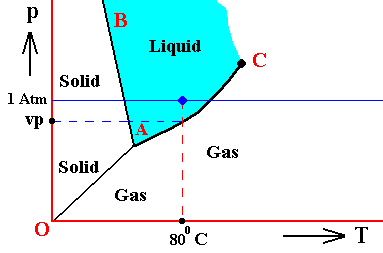
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
     If (as an example) some quantity of H₂O finds itself at a temperature of 80⁰C (or any other temperature between 0⁰ and 100⁰) and under a pressure of 1 Atm, and, at the same time, finds itself in the liquid state, then it is as such stable. The liquid will neither boil nor freeze. We have to do with a bivariant equilibrium (F = 2), and, as we have found out above, this holds for any interior volume of that given liquid. In the graph we can see that the vapor pressure (vp) of liquid water at 80⁰C (which is a property of H₂O) is lower than 1 Atm (which is the pressure under which the system -- in this particular case -- is supposed to be). And if the system consists of H₂O only, then the actual pressure of the water vapor above the water has a pressure of 1 Atm, so a part of this water vapor will condense until the pressure has decreased from 1 Atm to  vp .  The system has then arrived at the water-vapor curve of liquid water (at 80⁰C) and finds itself in a monovariant equilibrium (between liquid and gas).
If the system of H₂O is contained within a matrix of air (supplementing the  vp  pressure to 1 Atm), then the equilibrium water-vapor pressure at 80⁰C, which is (always)  vp ,  is lower than the pressure (1 Atm) of the system, meaning that the water will not boil. We can see that, although the actual water-vapor pressure (as partial pressure) is equal to the equilibrium vapor pressure  vp  (at 80⁰C), and in this way suggesting the presence of a monovariant equilibrium between liquid and gas, the extra pressure of the air, resulting in 1 Atm pressure under which the system stands, presses the system, from the vapor-pressure curve, up into the 'liquid' area of the triple-point diagram. We must note that if the system of H₂O as embedded in air is to be in equilibrium, the water vapor must be prevented from diffusing away from the system, otherwise all the liquid will eventually be evaporated. The system must therefore be contained in a closed vessel. But then a pressure will result that is a little above 1 Atm. We can understand this as follows :  If we have a vessel partially filled with liquid water, and open to the atmosphere, the actual vapor pressure will remain below the equilibrium vapor pressure of liquid water at the given temperature, thanks to the diffusing away of the water vapor into the atmosphere. Therefore all the water will eventually evaporate. To prevent this we close the vessel. The pressure of the vapor is now allowed to increase (thanks to evaporation from the liquid) until it has become equal to the equilibrium vapor pressure (of liquid water at the given temperature). It is then that we have equilibrium between the liquid and its gas. But the vapor that has in this way been added to the air above the liquid (but still in the closed vessel) increases the overall pressure, resulting in a pressure a little above 1 Atm. This can easily be such that the system still resides within the 'liquid' area of the triple-point diagram.
     If, on the other hand, when still existing under the same temperature-pressure conditions (80⁰C and 1 Atm), this same quantity of H₂O finds itself in the gaseous state, then it is unstable (it is undercooled vapor), and directly condenses into liquid as soon as it receives an appropriate nudge (for example the presence of dust particles that represent suitable condensation nuclei ). Also in this case, when the system is pure H₂O, the initial gas (which is 100 percent water vapor) condenses until it will be in equilibrium with the resulting liquid, entailing in this way a decrease in pressure from 1 Atm to the equilibrium vapor pressure of liquid water at the given temperature (80⁰C), which pressure is given as  vp  in the above Figure. In this way a monovariant equilibrium is established between water and water vapor. A bivariant equilibrium can be established when the decrease in pressure is compensated for by air, that is to say when the H₂O system is not considered to be a pure system, but embedded within air. Also here the vessel must be closed, resulting in an overall pressure a little above 1 Atm, which can be such that the system still resides in the 'liquid' area of the triple point diagram, and so is in equilibrium with itself, which is a bivariant equilibrium.
     And also when our quantity of H₂O finds itself in the solid state (when still existing under the same temperature-pressure conditions (80⁰C and 1 Atm)), it is unstable, and directly melts, i.e. transforms spontaneously into a liquid.
It is important to realize that because we here (i.e. in the present example) first of all treat the ice-water-steam system as it is in itself, the pressure of 1 Atm under which the system is supposed to be, has no special significance, it has been choosen arbitrarily.

The next Figure indicates the above described pressure adjustment of the (pure) system to the equilibrium pressure, for the case that the quantity of H₂O initially finds itself in the gaseous state while under temperature-pressure conditions of 80⁰C and 1 Atm, i.e. where we have to do with an undercooled vapor. If the system is not embedded in air, i.e. if the H₂O system is pure, we have water vapor having a pressure of 1 Atm. This is well above the equilibrium vapor-pressure of liquid water at 80⁰C, so this vapor will (under appropriate nucleation conditions) start to condense until equilibrium is reached between the liquid and the gas phase (as described above). This is a monovariant equilibrium (F = 1). So it is evident that during condensation water vapor is consumed by the forming liquid, implying that the pressure is decreasing. This pressure will keep on decreasing until it reaches the equilibrium pressure (vp) at 80⁰C. In all this we must imagine that we start with a rigid container of volume V containing only water vapor. The vapor is supposed to have a temperature of 80⁰C, and there is so much of it in the container that its pressure is initially 1 Atm. As the vapor partially condenses the temperature of the system remains constant at 80⁰C, but the pressure decreases.

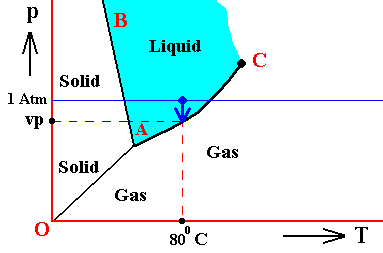
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase. Initial pressure of the system is 1 Atm.
Pressure adjustment.
As the water vapor condenses while the temperature remains constant, its pressure decreases until it reaches  vp ,  which is the equilibrium pressure for 80⁰C. This pressure reduction is indicated by the arrow.

The average kinetic energies of particles in gaseous and liquid phases at the boiling point are equal. However, energy is required in order to maintain boiling with the resultant transfer of matter from the liquid to the gaseous phase. The heat added does not increase the temperature of the liquid at the boiling point but provides the energy necessary for the most energetic particles to continue to escape  [ Recall that when a liquid is evaporating, the most energetic particles escape, resulting in the average kinetic energy of the liquid to decrease. So it becomes more and more difficult for the (slower) particles to escape. Consequently, to keep the evaporation process going, energy must be supplied. ] .  The quantity of heat energy required to transform 1g of a substance at its boiling point from a liquid into a gas is called its  heat of vaporization.  The heat of vaporization of water is 540 cal/g, a value that is rather large compared to other liquids. Its size is a reflection of the strong attractive forces between neighboring water molecules in the liquid phase.
While the heats of vaporization of substances are usually listed in calories per gram, it should be pointed out again that mass per se is not of primary importance in understanding matter. The number of atoms  [ or molecules ]  involved in a phenomenon is more basic  [ So the heat of vaporization is better expressed in terms of calories per mole of compound, where a "mole" is the number of grams equal to the molecular weight of the compound, and where in turn the "molecular weight" is the number of times that one molecule of the compound is heavier than 1/12 of an atom of a certain isotope of carbon, or, more roughly, is heavier than one hydrogen atom. ]  [...] .  If the heat of vaporization per mole of a substance is divided by its boiling point on the Kelvin scale, an average value of 21 cal/mole-deg  [ i.e. calories-per-mole per degree Kelvin ]  is obtained for many liquids.
The empirical observation that for most liquids the quotient of the molar heat of vaporization and the boiling point is nearly always 21 cal/mole-deg is called Trouton's rule. Why this ratio is constant is an intriguing question. At the boiling point, the relatively unified liquid phase is transformed into a random gaseous phase with no change in the average kinetic energy of particles. However, energy has been required for the process and has been utilized in randomizing the system. At the boiling point vapors can be liquefied with the recovery of energy equal to the heat of vaporization. In the liquefaction process matter becomes less random and more ordered. The constant value of 21 cal/mole-deg indicates the constant relation between heat energy and temperature for the randomization process.
The term  entropy  (S) is used to indicate the degree of randomness of a system. As the molecular chaos of matter increases, its entropy is said to increase. The entropy of matter in the liquid phase is less than that in the gaseous phase, and the value 21 cal/mole-deg is a measure of the change in entropy (DELTA S) for the transformation. Thus, for the general process of converting matter from the liquid to the gaseous phase, the increase in the randomness of the system is a constant.
In the case of water and alcohol, the Trouton's constant is approximately 26 cal/mole-deg, a higher-than-average value. Since the value represents a change in entropy for the process of vaporization, it must be concluded that there is something about the molecular structure of these compounds that leads to higher than average ordering in the liquid state  [ because the 'distance' on the scale of degrees of order from the gas state to the liquid state of each of these compounds (water and alcohol) is greater than that in many other compounds, while the degree of order of gases of different substances at the same temperatures is supposed to be the same. So having to traverse a longer distance along the scale of lowest-degree order (randomness) - higher-degree order, than is the case in other substances, lets us end up with a higher degree of order of the liquid in water and in alcohol than in that of other substances. ].  If this is the case, then the change in the degree of molecular chaos would be larger for the vaporization process that leads to the very random gaseous state  [ And indeed, in an earlier document, we have seen that liquid water does have some structure ].

So to have a substance at its boiling point corresponding to the prevailing pressure, is not enough to get it boiling. Energy must be supplied for randomizing the system.

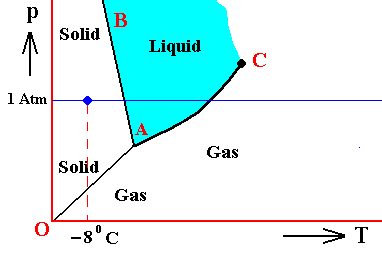
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
     If (as an example) some quantity of H₂O finds itself at a temperature of  -8⁰C (or any other temperature (moderately) below its normal freezing point) and under a pressure of 1 Atm, and, at the same time, finds itself in the solid state, then it is as such stable.
The ice will neither melt nor sublimate. We have to do with a bivariant equilibrium (F = 2). Also in this case we consider an interior volume of this ice. Such a volume is under the mentioned temperature-pressure conditions (-8⁰C, 1 Atm) in equilibrium with itself.
     If, on the other hand, when still existing under the same temperature-pressure conditions (-8⁰C and 1 Atm), it finds itself in the liquid state (which we call undercooled water), then it is unstable, and directly freezes as soon as it receives an appropriate nudge (for example when an ice fragment is added). The resulting ice is then in equilibrium with itself (bivariant equilibrium) when only considering its interior (i.e. any interior volume of it).
     And, finally, when it finds itself in the gaseous state (when still existing under the same temperature-pressure conditions (-8⁰C and 1 Atm)), it also is unstable, and transforms into the solid state, as soon as it receives the appropriate nudge. It is to be expected that in this case we first see a transformation into the liquid state, and then -- when conditions for ice nuleation are satisfied (for example the presence of ice, or the presence of dust particles such as providing a template for the ice structure to be formed) -- a transformation into the solid state. This solid phase (ice) is in equilibrium with itself when considering only its interior.

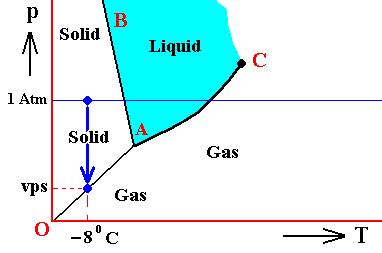
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase. Initial pressure of the system is 1 Atm.
Pressure readjustment.
As the liquid water freezes (while the temperature does not change), the pressure of the system decreases until it reaches  vps ,  which is the equilibrium pressure for  -8⁰C (i.e. the pressure has become equal to the equilibrium water-vapor pressure of ice at a temperature  -8⁰C). This pressure reduction is indicated by the arrow.

I again emphasize, that in the above examples we have been talking about the ice-water-steam system as it is in itself, as a system of phases. In the case of the formation of snow, water droplets, etc., in the earth's atmosphere, some additional features pop up, like under-saturation, saturation and super-saturation of water vapor in the air. Also this will be discussed below.

Just above we had described that, as a result of the precipitation of water vapor onto the ice, the pressure -- of the water vapor and, by implication, of the system (which consists of H₂O only) -- will decrease, until a monovariant equilibrium is established between vapor and ice. In what cases then, will we have a bivariant equilibrium? Well the latter could be established if the decrease of the pressure of the water vapor (as being originally the pressure of the pure H₂O system) is neutralized by that of another gas or mixture of gas, say, air. Only then the above described system will remain at the pressure of 1 Atm, implying that it is, and remains, positioned within the 'solid' area of the triple-point diagram. And then we indeed have to do with a bivariant equilibrium as described above. In fact the pressure of the system will end up a little above 1 Atm (but with this it is still possible that the system resides in the 'solid' area of the triple-point diagram). This is because when we want to maintain equilibrium between the solid and the gas, the container must be closed :  if it is open, then the water vapor that comes from the ice will diffuse into the broader environment, preventing in this way the establishing of the equilibrium. Eventually the whole solid will evaporate (just as it is in the case of liquids). So the container must be closed. But then the pressure will rise a little above 1 Atm, the excess being exactly the equilibrium vapor pressure of ice at the temperature of the experiment (which was  -8⁰C).

Also it is important to know that during a phase transition the temperature remains constant :
When a solid is heated, the supplied heat (which is coming from the environment of the system) increases the average kinetic energy of the constituent particles of the solid, which means that the temperature of this solid rises. When, finally, the melting point has been reached, the heat, that is still being supplied, is used to partially randomize the system. The system goes from an orderly state to a moderately disordered state. Only after the solid has been totally molten, the temperature will rise again.
This heat -- the heat of fusion -- consumed at the melting point, will be recovered when the liquid is set to freeze (crystallize) again :  heat of crystallization :  During crystallization from the melt this heat is returned to the environment of the system :  also here the temperature of the system remains constant (melting point).
The same is the case fo the other phase transition :
When a liquid is heated, the supplied heat (which is coming from the environment of the system) increases the average kinetic energy of the constituent particles of the liquid, which means that the temperature of this liquid rises. When, finally, the boiling point has been reached, the heat, that is still being supplied, is used to fully randomize the system. The system goes from a moderately disordered state to a totally disordered state. Only after the liquid has been totally transformed into vapor, the temperature will rise again.
This heat -- the heat of vaporization -- consumed at the boiling point, will be recovered when the vapor is set to condense again :  heat of condensation :  During condensation of the vapor this heat is returned to the environment of the system (as it happens in the cooler of a distillation device) :  also here the temperature of the system remains constant (boiling point).

While in the above two cases, apart from the system's spontaneous readjustment to equilibrium pressure, the temperature-pressure conditions were supposed to remain constant, which means that, while describing some phase transition that takes place, we do not move over the diagram (i.e. we do not actively change the specified temperature-pressure coordinates),  in the next case we actively change a condition to the effect that we change one of the temperature-pressure coordinates, which means that, in the diagram, we change position, we move over the diagram, and so can enter from one phase into another.

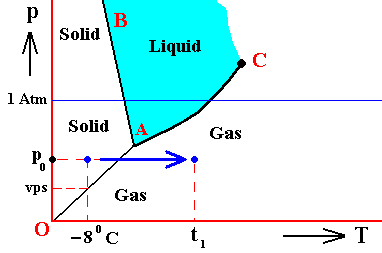
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
If (as an example) some quantity of H₂O finds itself at a temperature of -8⁰C (or any other temperature below its normal freezing point) and under a pressure of  p₀ Atm (i.e. some pressure, lower than 1 Atm, and also lower than the triple-point pressure), and, at the same time, finds itself in the solid state, then it is as such stable.  If we now raise the temperature from  -8⁰C  to  t₁⁰ (i.e. a temperature above the triple-point temperature), then the ice will evaporate, i.e. the solid phase transforms into the gaseous phase.  In the diagram this is expressed by a movement indicated by the arrow.
Let us describe more precisely the initial condition of this experiment (ice under a pressure of p₀ Atm and having a temperature of  -8⁰C).
In the present experiment we had set the pressure of the system at  p₀  Atm (wich is lower than 1 Atm, and, what is especially relevant, it is lower than the triple-point pressure of H₂O). But as we can see in the diagram, the equilibrium vapor-pressure of ice at  -8⁰C (vps) is lower than  p₀ .  So in order to have the system in equilibrium, we must now see the mentioned equilibrium vapor pressure  vps  (of ice at  -8⁰C) as being a  p a r t i a l  pressure. The remaining part of the pressure is taken to be caused by  a i r  that is now supposed to be present in the system (making a total pressure of  p₀ ). That the partial pressure, exerted by the water vapor is  vps,  means that when the air were taken away, without changing the volume of the system, the water vapor would exert a pressure of  vps.
If the equality between the actual prevailing vapor pressure and the equilibrium vapor pressure of ice (at  -8⁰C) is to be maintained, the vessel (containing the ice, water vapor and air) must be closed.
The significance of the fact that the actual prevailing pressure of the water vapor (in the vessel) is equal to the equilibrium vapor-pressure of ice at that temperature, is that it guarantees that the traffic of water vapor to the ice (i.e. the precipitation of water vapor onto the ice) exactly balances the traffic of water molecules out of the ice, resulting in a constant net amount of ice.
The system itself -- as it is in its initial state -- stands under a pressure (p₀) that is higher than the equilibrium vapor pressure of ice at the given temperature (vps), which means that the position of the system is above the equilibrium vapor pressure curve of ice (sublimation curve), which in turn means that the system entirely resides in the 'solid' area of the triple point diagram, in this way representing a bivariant equilibrium.

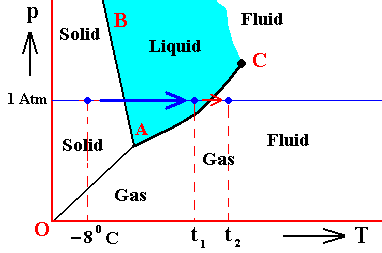
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
If (as an example) some quantity of H₂O finds itself at a temperature of  -8⁰C (or any other temperature below its normal freezing point) and under a pressure of  1 Atm, and, at the same time, finds itself in the solid state, then it is as such stable.  Also here we assume air to be present in the system, its partial pressure supplementing the equilibrium water-vapor pressure of ice at  -8⁰C (which is lower than 1 Atm) to a pressure of 1 Atm.
If we now raise the temperature from  -8⁰C  to  t₁⁰ (i.e. a temperature above the triple-point temperature, but below the boiling point at 1 Atm), then the ice will melt, i.e. the solid phase transforms into the liquid phase.  In the diagram this is expressed by a movement indicated by the blue arrow.
If we then continue to raise the temperature (from  t₁) to  t₂ ,  i.e. to a temperature lying above the boiling point at 1 Atm (but below the critical temperature), then the liquid will transform into the gaseous phase. This is indicated by the red arrow. If the temperature is raised still further, eventually the supra-critical area will be reached, where there is no difference anymore between the liquid and the gaseous states. This super-critical phase is called fluid.

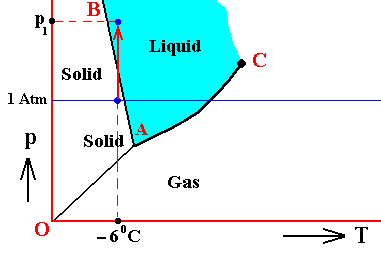
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
If (as an example) some quantity of H₂O finds itself at a temperature of -6⁰C (or any other temperature below its normal freezing point) and under a pressure of  1 Atm, and, at the same time, finds itself in the solid state, then it is as such stable.  If we now raise the  pressure  (while holding the temperature constant) (from 1 Atm) to  p₁  (i.e. a pressure well above 1 Atm), then the ice will melt (because now going toward a smaller volume, relieves the pressure on the system), i.e. the solid state transforms into the liquid state. This transition is indicated by a red arrow.

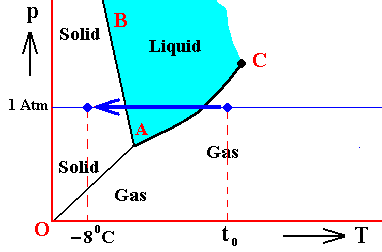
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
The Figure illustrates the generation of ice from hot water vapor.
If some quantity of H₂O finds itself at a temperature of  t₀⁰C  (meaning a temperature well above its normal boiling point), and at a pressure of 1 Atm, and, at the same time finds itself in the gaseous state, then it is as such stable. If we now rapidly cool the system all the way down to -8⁰C (or any other temperature below the normal freezing point of water), then the gaseous state will become unstable, because the system has moved into the solid area of the diagram. It will change to the solid state, but, generally, not until nucleation events produce crystal embryos of sufficiently large size. It is to be expected that this transition goes through an intermediate state, the liquid state, as it happens in the formation of snowflakes from (cold) water vapor. If the pressure of the system were below the triple point pressure, then the vapor immediately transforms into ice without going through any intermediate phase.

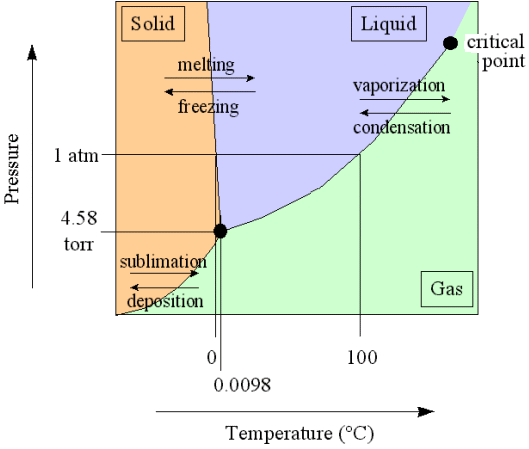
Phase diagram of  H₂O (water), after LIBBRECHT, www.snowcrystals.com.
According to LIBBRECHT the triple point pressure of water is 6.1 mbar, and the triple point temperature is 0.0098⁰C.  (1 mbar = 0.75 mm mercury = 0.001 Atm) (1 mm mercury = 1 torr).

The water-vapor pressure under the above LINK represents :

• The water-vapor pressures of liquid water, where (as defined) water is in equilibrium with its vapor at the given above-zero temperatures and 1 Atm ( = 1000 mbar) system pressure.  Only at 100⁰C the vapor pressure (of liquid water) will reach the system pressure of 1 Atm and the water will start to boil.
• The water-vapor pressures of liquid water, where (as defined) water is in equilibrium with its vapor at the given below-zero temperatures and 1 Atm system pressure. In these cases the water is supercooled.
• The water-vapor pressures of ice (red part of graph), where (as defined) ice is in equilibrium with its water vapor at the given below-zero temperatures and 1 Atm system pressure.

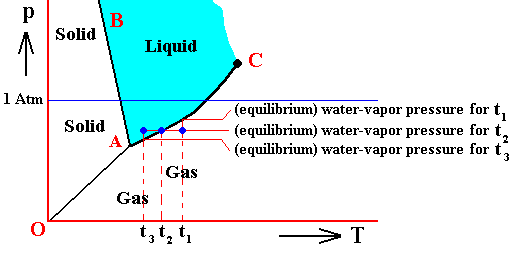
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
The Figure describes the first stage in the formation of snow, namely air that becomes supersaturated with water vapor. Water-vapor pressures are indicated by horizontal lines (levels).
The actually prevailing water-vapor pressure, happens -- as is supposed for the present case -- to be equal to the equilibrium water-vapor pressure (of liquid water) belonging to temperature  t₂ .
The equilibrium water-vapor pressure (of liquid water) at temperature  t₁  is indicated. It is higher than the actually prevailing water-vapor pressure, and consequently, higher than the equilibrium water-vapor pressure at temperature  t₂ .
The equilibrium water-vapor pressure (of liquid water) at temperature  t₃  is indicated. It is lower than the actually prevailing water-vapor pressure (and consequently, lower than the equilibrium water-vapor pressure at temperature  t₂  as well as that of  t₁ ).  And just because of this equilibrium water-vapor pressure belonging to  t₃  being lower than the actually prevailing water-vapor pressure (and the latter thus being higher), the air is supersaturated with water vapor.
In the Figure all this is happening if we go from temperature  t₁ ,  via  t₂  to temperature  t₃ .  In this way we have arrived, from the gas area of the diagram into its liquid area, and because (initially) we still have to do with (water) vapor, the system has become unstable. The water vapor will spontaneously turn into water droplets as soon as appropriate condensation nuclei are present.

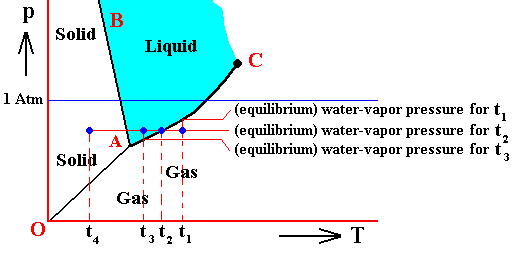
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
The Figure describes, in addition to the first stage (explained above), the second stage in the formation of snow, namely the solidification of the water droplets.
When the temperature of the water droplets is lowered below the normal freezing point (in the Figure all the way down to  t₄ ),  the droplets will not readily freeze despite the low temperature. The system has (again) become unstable. But as soon as appropriate ice nucleation particles are present, the droplets will spontaneouly freeze. A supercooled cloud droplet may freeze around  -10⁰C  (14⁰F) if it contains an average dust particle, or perhaps as high as  -6⁰C  (21⁰F) for the best ice nuclei (LIBBRECHT, op. cit. p.62). These frozen drops are, however, not yet snowflakes.

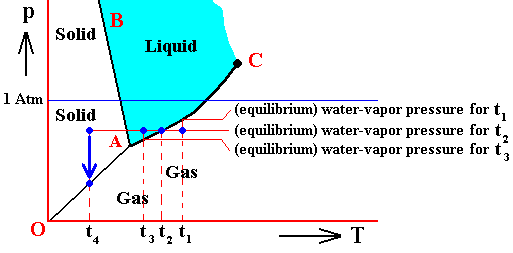
Figure above :  (Approximate) Phase diagram of  H₂O (water) as a one-component system (C = 1).  The phases are Ice, Water and Water vapor.  A = triple point. Blue area signifies the stability area of the liquid phase.
The Figure describes, in addition to the first and second stages (explained above), the third and final stage in the formation of snow, namely the growth of the solidified water droplets, resulting in (growing) snowflakes.
The vapor from the remaining droplets, together with remaining water vapor that was still present, precipitate onto the frozen droplets and onto the already existing snowflakes, lowering in this way the (actually prevailing) vapor pressure, until equilibrium between ice and water vapor is established, as indicated by the vertical arrow in the diagram. This equilibrium consists in the actual prevailing water vapor pressure becoming equal to the equilibrium vapor pressure of ice at the given temperature. The growth of snowflakes, i.e. their increase in size in virtue of the deposition of water molecules, reflects the movement of the system toward this equilibrium (which will probably not actually be reached).

In addition to the above considered one-component systems (C = 1), there are  two-component systems (C = 2), which we will consider very briefly.
Generally we get, according to the phase rule P + F = C + 2, for two-component systems (because C = 2), P + F = 4.  So the number of phases plus the number of degrees of freedom equals four.
If we have to do with an invariant equilibrium (F = 0), then P = 4, i.e. the number of phases is four. So in the case of the presence of four phases the system is completely determined, i.e. one cannot change either pressure or temperature or volume or concentration of the phases (with respect to the latter, that means (one cannot change) their composition), without disturbing the equilibrium of the invariant system.

Generally we get, according to the phase rule P + F = C + 2, for three-component systems (because C = 3), P + F = 5.  So the number of phases plus the number of degrees of freedom equals five.
This leads, for the invariant equilibrium (F = 0) to a quintupel point with five different phases. The monovariant equilibrium (F = 1) possesses four phases.
Multi-component systems consist of four or more independent components. We will not discuss them further.

This concludes our consideration of the theory of phases. We have emphasized one-component systems, because having in mind simple crystallization processes. In such a process crystals of a single given substance appear from their melt, solution or vapor. This is a phase transition from either a liquid phase or a gas phase into the solid phase. Also the reverse processes are automatically considered :  melting, dissolution and evaporation. The theory of phases considers the general conditions for the  existence  of these phases. Where (next document) we come to speak about the very  generation  of crystals (for which the mentioned conditions are necessary to begin with), we will consider how crystallization gets started, because even when crystals of a given substance are in principle possible to exist, they often do not appear in the absence of some 'nudge', for instance the appearing (in the melt, solution or vapor) of crystal embryos of sufficiently large size. A very important feature that is involved in these matters is the surface energy of an incipient crystal. It contributes to the total Gibbs free energy, and must be counteracted by an appropriate decrease in free enegy of the crystal with respect to its melt, solution or vapor.

e-mail : 

Back to Homepage

Back to Contents

Back to Part I

Back to Part II

Back to Part III

Back to Part IV

Back to Part V

Back to Part VI

Back to Part VII

Back to Part VIII

Back to Part IX

Back to Part X

Back to Part XI

Back to Part XII

Back to Part XIII

Back to Part XIV

Back to Part XV

Back to Part XV (Sequel-1)

Back to Part XV (Sequel-2)

Back to Part XV (Sequel-3)

Back to Part XVI

Back to Part XVII

Back to Part XVIII

Back to Part XIX

Back to Part XX

Back to Part XXI

Back to Part XXII

Back to Part XXIII

Back to Part XXIV

Back to Part XXV

Back to Part XXVI

Back to Part XXVII

Back to Part XXVIII

Back to Part XXIX

Back to Part XXIX (Sequel-1)

Back to Part XXIX (Sequel-2)

Back to Part XXIX (Sequel-3)

Back to Part XXIX (Sequel-4)

Back to Part XXIX (Sequel-5)

Back to Part XXIX (Sequel-6)

Back to Part XXIX (Sequel-7)

Back to Part XXIX (Sequel-8)

Back to Part XXIX (Sequel-9)

Back to Part XXIX (Sequel-10)

Back to Part XXIX (Sequel-11)

Back to Part XXIX (Sequel-12)